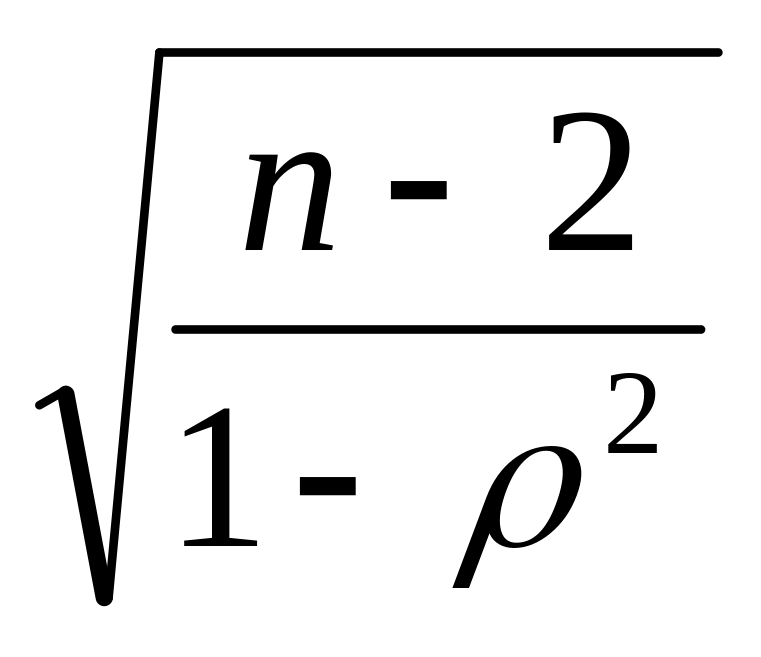При импортировании данных из других источников вы, возможно, уже успели обнаружить, что Excel иногда некорректно импортирует значения. В частности, он может принять ваши числа за текст. И тогда, например, при суммировании диапазона значений формула СУММ возвращает 0 — хотя диапазон, по всей видимости, содержит числовые значения.
Часто Excel сообщает вам об этих «нечислах», отображая смарт-тег, который позволяет преобразовать текст в числа. Если смарт-тег не отображается, вы можете использовать следующий метод, чтобы указать Excel изменить эти «нечисловые» числа на их фактические значения. Выполните следующие действия.
- Активизируйте любую пустую ячейку на листе.
- Нажмите Ctrl+C, чтобы скопировать пустую ячейку.
- Выберите диапазон, содержащий проблематичные значения.
- Выберите Главная ► Буфер обмена ► Вставить ► Специальная вставка для открытия диалогового окна Специальная вставка.
- В окне Специальная вставка установите переключатель Операция в положение сложить.
- Нажмите кнопку ОК.
Excel ничего не добавит к значениям, но в процессе укажет этим ячейкам иметь фактические значения.
По теме
Новые публикации
Содержание
- При использовании функции линейная регрессия (ЛИНЕЙН) в Excel возвращается неверный результат
- Проблемы
- Причина
- Обходное решение
- Случай 1: диапазоны x-value и y перекрываются
- Случай 2: количество строк меньше числа столбцов x-Columns.
- Случай 3: указывается нулевая константа
- Дополнительная информация
- Ссылки
- Входной интервал содержит нечисловые данные что делать?
- Работа с инструментом «Регрессия» в Microsoft Excel
- Использование Пакета анализа EXCEL для построения простой линейной регрессионной модели
- Регрессия входной интервал содержит нечисловые данные
- Статистический анализ в excel Назначение и возможности пакета анализа
- Установка пакета анализа.
- Вызов пакета анализа
- Корреляция
- Регрессионный анализ. Построение статических однофакторных моделей
- Практическая работа 1. Регрессионный анализ. Построение статических однофакторных моделей.
- Часть I.
- Часть II.
- Варианты заданий к практической работе 1.
При использовании функции линейная регрессия (ЛИНЕЙН) в Excel возвращается неверный результат
Проблемы
При использовании функции ЛИНЕЙН на листе в Microsoft Excel результаты статистического вывода могут возвращать неверные значения. Средство регрессия в окне «пакет анализа» может также возвращать неверные значения.
Причина
Результат, возвращаемый функцией ЛИНЕЙН, может быть неправильным, если выполняется одно или несколько из указанных ниже условий.
Диапазон значений x перекрывает диапазон значений y.
Количество строк в диапазоне входных данных меньше числа столбцов в общем диапазоне (x-value + y-Value).
Вы задаете нулевую константу (для третьего аргумента функции ЛИНЕЙН установите значение истина).
Обходное решение
Случай 1: диапазоны x-value и y перекрываются
Если диапазоны x-value и y перекрываются, функция ЛИНЕЙН возвращает неверные значения во всех ячейках результата. Нормальная статистическая вероятность запрещает значения в диапазонах x и y для перекрытия (повторяющиеся друг друга). Не перекрывают диапазоны x и y при ссылке на ячейки в формуле.Примечание. Средство регрессия предупреждает об этой проблеме и не продолжает работу. Вы можете использовать средство регрессия вместо функции ЛИНЕЙН. В Microsoft Office Excel 2007 вы можете найти инструмент регрессия, щелкнув анализ данных в группе анализ на вкладке данные . В Microsoft Office Excel 2003 и более ранних версиях Excel можно найти инструмент регрессия, выбрав пункт анализ данных в меню Сервис .
Случай 2: количество строк меньше числа столбцов x-Columns.
Статистические функции не действительны, так как количество строк должно быть меньше числа столбцов x (переменных). Количество строк данных должно быть больше количества столбцов данных (столбцов x и y).
Случай 3: указывается нулевая константа
Не указывайте нулевые константы (b = 0) в функции.
Дополнительная информация
Средство регрессия входит в пакет анализа. Пакет анализа — это программа надстройки Excel. Оно доступно при установке Microsoft Office или Excel. Прежде чем использовать средство регрессия в Excel, вы должны загрузить анализ ToolPak.To в Excel 2007, выполнив указанные ниже действия.
Нажмите кнопку Microsoft Office, затем нажмите кнопку Параметры Excel.
Выберите пункт надстройки, а затем в поле Управление выберите пункт надстройки Excel .
Нажмите кнопку Перейти.
В окне Доступные надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК.Примечание. Если в списке Доступные надстройки не указан Пакет анализа , нажмите кнопку Обзор , чтобы найти его.
Чтобы сделать это в Excel 2003 и более ранних версиях Excel, выполните указанные ниже действия.
В меню Сервис выберите пунктнадстройки.
В диалоговом окне надстройки выберите Пакет анализаи нажмите кнопку ОК,Обратите внимание на то, что Пакет анализа не указан в поле Доступные надстройки, нажмите кнопку Обзор , чтобы найти его.
Ссылки
Статистические вычисления на цифровом компьютере. Уильям J. Hemmerle. Blaisdell компания публикации: 1967. Глава 3, «вычисления с несколькими регрессиями» и раздел 3.2.1, «теория для предварительной регрессии».
Источник
Входной интервал содержит нечисловые данные что делать?
Работа с инструментом «Регрессия» в Microsoft Excel
Открыв рабочую книгу и введя в нее исходные данные для построения уравнения регрессии, вызываем надстройку «Регрессия»: Данные — Анализ данных — Регрессия.
Диалоговое окно «Регрессия». В первое окно «Входной интервал Y» вводим данные объясняемой переменной — у, диапазон должен состоять из одного столбца. Во второе окно «Входной интервал X» вводим данные объясняющих переменных — х. На рис. П.1 представлены у. $С$2:$С$13, х: $В$2:$В$13. Длины интервалов должны быть одинаковы. Если строится уравнение множественной регрессии, то данные объясняющих переменных вводятся в окно «Входной интерват X» соответствующим образом. На рис. П.2 представлены у: $D$2:$D$13, xt—x2: $В2:$С$13. Максималь- ное число независимых объясняющих переменных равно 16.
Рис. П. 1. Задание парной регрессии
Ставим «галочку» в окно «Метки», если в отчете Microsoft Excel требуется знать, к какой из объясняющих переменных относятся результирующие данные.
Если исследователю не требуется константа Ь , то ставим «галочку» в окно «Константа — ноль». Линия регрессии пройдет через начало координат.
Рис. П.2. Задание множественной регрессии
«Уровень надежности». По умолчанию программа строит уравнение регрессии для доверительной вероятности (уровень надежности) 0,95. Если требуется другая величина, ставим «галочку» в окно «Уровень надежности» и в окно, помеченное символом «%», вводим требуемую величину уровня надежности десятичной дробью.
«Параметры вывода». Указываем, куда вывести результаты регрессионного анализа: на этом листе, как указано на обоих рисунках, на другой рабочий лист или в новую рабочую книгу.
«Остатки». Выбираем то, что требуется исследователю, и ставим «галочку». Можно одновременно пометить несколько окон. Подробная информация дана в справке но инструменту «Регрессия».
Заполнив диалоговое окно «Регрессия», нажимаем кнопку ОК. Программа выводит отчет «Вывод итогов» в виде трех таблиц (рис. П.З, приведено для двух объясняющих переменных).
Приведем описание таблиц (первых двух — в табл. П1.1 и П1.2 соответственно, третьей — в текстовом виде).
Описание первой таблицы
Наименование в отчете
Коэффициент множественной корреляции, индекс корреляции
Коэффициент детерминации, R 2
Скорректированный К 2
Наименование в отчете
Среднее квадратическое отклонение от модели
Рис. П.З. Результаты работы программы
Описание третьей таблицы
Данные первой строки относятся к коэффициенту уравнения регрессии Ь , данные второй строки — к коэффициенту Ьи третьей — к Ь2 и далее до коэффициента Ьт, но числу объясняющих переменных в уравнении.
Метки, если поставлена галочка в окно «Метки». У-пересечение для коэффициента/> , далее но всем объясняющим переменным.
Значения коэффициентов уравнения регрессии Ь , Ьь . Ьт.
Стандартная ошибка коэффициента регрессии 5^, 5Л). Sbm.
Статистическая значимость коэффициента регрессии (^-статистика) для а = 0,05 tw . tbm.
P-значение — это значение уровней значимости, соответствующее вычисленным ^статистикам коэффициентов.
Нижние 95% и Верхние 95% — это нижние и верхние границы 95%-ных доверительных интервалов для коэффициентов уравнения регрессии. Если в окно «Уровень надежности» не вводилось другое значение доверительной вероятности, то последние два столбца дублируют предыдущие два столбца. Если в окно «Уровень надежности» было введено другое значение доверительной вероятности у, то последние два столбца содержат значения соответственно нижней и верхней границы у-процентных доверительных интервалов.
Описание второй таблицы
df — число степеней свободы
SS — сумма квадратов
MS = SS/df — дисперсия на одну степень свободы
Использование Пакета анализа EXCEL для построения простой линейной регрессионной модели
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Проведем простой регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .
Эффективно использовать надстройку Пакет анализа для целей регрессионного анализа могут только пользователи знакомые с теорией регрессионного анализа .
В данной статье решены следующие задачи:
- Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
- Даны пояснения по разделам отчета, формированного надстройкой.
В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .
После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):
- Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
- Входной интервал Х : ссылка на значения переменной Х. В случае множественной регрессии (несколько переменных Х) нужно указать все столбцы со значениями Х. В случае множественной регрессии ссылку рекомендуется делать на диапазон с заголовками (в окне требуется установить галочку Метки );
- Константа-ноль : если галочка установлена, то надстройка подбирает линию регрессии, проходящую через точку Y=0 ( сдвиг будет равен 0);
- Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа. Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
- Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
- Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
- Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
- График остатков : Будет построена точечная диаграмма : значения остатков для всех значений Хi;
- График подбора: Будет построена точечная диаграмма: точки данных (X;Y) и линия регрессии ;
- График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .
В результате вычислений будет заполнен указанный Выходной интервал.
Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка, столбцы I:T ):
Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про простую линейную регрессию с помощью функций ЛИНЕЙН() , НАКЛОН() , ОТРЕЗОК() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.
Отчет, сформированный надстройкой, состоит из следующих разделов:
Раздел «Регрессионная статистика»:
- Множественный R. В случае простой линейной регрессии — это Коэффициент корреляции , функция КОРРЕЛ()
- R-квадрат . В случае простой линейной регрессии – это коэффициент детерминации , функция КВПИРСОН()
- Нормированный R-квадрат . См. про коэффициент детерминации .
- Стандартная ошибка . См. Стандартная ошибка регрессии ;
- Наблюдения . Количество значений Y.
Раздел « Дисперсионный анализ »:
- df – степени свободы (Degrees of Freedom).
- SS – сумма квадратов (Sum of Squares)
- MS – SS/df (MSR и MSE)
- F – значение статистики F (MSR/MSE)
- ЗначимостьF – p-значение, функция F.РАСП.ПХ()
- Коэффициенты : оценка параметров модели а и b. См. Оценка неизвестных параметров .
- Стандартная ошибка : Стандартные ошибки вышеуказанных статистик
- t-статистика : значение тестовой статистики t0. См. Проверка значимости взаимосвязи переменных
- P-Значение : См. Проверка значимости взаимосвязи переменных
- Нижние 95% и Верхние 95%: границы доверительных интервалов для оценок неизвестных параметров модели а и b .
Регрессия входной интервал содержит нечисловые данные
трюки • приёмы • решения
При импортировании данных из других источников вы, возможно, уже успели обнаружить, что Excel иногда некорректно импортирует значения. В частности, он может принять ваши числа за текст. И тогда, например, при суммировании диапазона значений формула СУММ возвращает 0 — хотя диапазон, по всей видимости, содержит числовые значения.
Часто Excel сообщает вам об этих «нечислах», отображая смарт-тег, который позволяет преобразовать текст в числа. Если смарт-тег не отображается, вы можете использовать следующий метод, чтобы указать Excel изменить эти «нечисловые» числа на их фактические значения. Выполните следующие действия.
- Активизируйте любую пустую ячейку на листе.
- Нажмите Ctrl+C, чтобы скопировать пустую ячейку.
- Выберите диапазон, содержащий проблематичные значения.
- Выберите Главная ► Буфер обмена ► Вставить ► Специальная вставка для открытия диалогового окна Специальная вставка.
- В окне Специальная вставка установите переключатель Операция в положение сложить.
- Нажмите кнопку ОК.
Excel ничего не добавит к значениям, но в процессе укажет этим ячейкам иметь фактические значения.
Входной интервал. Нужно ввести ссылку на интервал данных рабочего листа, подлежащих анализу. Excel также прелагает группирование входных данных по строкам или столбцам. Если во входной интервал включаются метки (заголовки строк или столбцов данных), необходимо установит флажок Метки,в противном случае Excel выдаст предупреждающее сообщение.
Метки. Если входной интервал не включает меток, снимите флажок Метки. Excel генерирует соответствующие метки данных для выходной таблицы (Строка 1, Строка 2, или Столбец 1, Столбец 2 и т.д.)
Выходные данные
Выходной интервал. Введите ссылку для верхней левой ячейки интервала, в который вы предполагаете вывести результирующую таблицу.
Новый рабочий лист. Этот параметр вставляет новый лист в рабочую книгу, где располагается текущий рабочий лист, и вставляет результаты в ячейку А1 нового листа. Используйте поле ввода рядом с параметром для задания имени нового листа.
Новая рабочая книга. Этот параметр создает новую рабочую книгу, добавляет новый рабочий лист и вставляет результаты в ячейку А1 нового листа.
Генерация случайных чисел
В имитационных моделях для описания реальных событий используются случайные величины и процессы. Когда имитационная модель рассчитывается на ЭВМ, то возникает необходимость реализации указанных процессов с максимально возможной точностью.
Для генерации случайных величин необходимо иметь возможность получать последовательность равномерно распределенных случайных чисел, т.е. чисел, которые ведут себя как независимые реализации или выборки случайной величины R, равномерно распределенной на единичном интервале [0,1]. Такие числа получают с помощью генераторов случайных чисел.
При помощи последовательности равномерно распределенных случайных чисел можно получить последовательности случайных величин, имеющих другие законы распределения.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10663 — 

Встроенные статистические функции используются для проведения статистического анализа данных.
Функция СРЗНАЧ вычисляет среднее арифметическое значение. Она игнорирует пустые, логические и текстовые ячейки и может использоваться вместо длинных формул. Например, для вычисления среднего значения данных в диапазоне ячеек В4:В15 можно использовать формулу:
Очевидно, что проще ввести = СРЗНАЧ(B4:B15).
Функция МЕДИАНА вычисляет медиану множества числовых значений.
Функция МОДА определяет значение, которое чаще других встречается во множестве чисел.
Функция МАКС вычисляет наибольшее значение в диапазоне.
Функция МИН вычисляет наименьшее значение в диапазоне.
Функция СЧЕТ определяет количество ячеек в заданном диапазоне, которые содержат числа, в том числе, даты и формулы, возвращающие числа.
Функции ДИСП и СТАНДОТКЛОН определяют дисперсию и стандартное отклонение чисел, в предположении что они образуют выборку.
Функции ДИСПР и СТАНДОТКЛОНП определяют дисперсию и стандартное отклонение для генеральной совокупности.
Функция НАКЛОН вычисляет коэффициент наклона линии линейной регрессии.
Функция ОТРЕЗОК вычисляет отрезок, отсекаемый на оси линией линейной регрессии.
Функция ПРЕДСКАЗ вычисляет теоретические значения y по линии линейной регрессии.
Если встроенных статистических функций недостаточно, можно обратиться к Пакету анализа .
Чтобы получить доступ к инструментам Пакета анализа необходимо:
· выполнить команду Сервис/Анализ данных;
· для использования инструмента анализа, выбрать его имя в списке и нажать кнопку ОК;
· заполнить открывшееся диалоговое окно (в большинстве случаев это означает задание входного диапазона с данными, которые вы собираетесь анализировать, указание верхней левой ячейки выходного диапазона, в который должны быть помещены результаты, и выбор нужных параметров. Группирование: установить переключатель в положение По столбцам или По строкам в зависимости от расположения данных во входном диапазоне. Установить переключатель в положение Метки в первой строке, если первая строка во входном диапазоне содержит названия столбцов или установить переключатель в положение Метки в первом столбце, если названия строк находятся в первом столбце входного диапазона. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически).
Если надстройка Анализ данных отсутствует, то ее можно подключить с помощью команды Сервис/Надстройки/Пакет анализа VBA ( Analysis ToolPak VBA ).
К инструментам Пакета анализа , например, относятся Описательная статистика , Корреляция , Регрессия .
Инструмент Описательная статистика предлагает таблицу основных статистических характеристик для одного или нескольких множеств входных значений ( Рис. 7.1 ):
Выходной интервал этого инструмента содержит следующие статистические характеристики: среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия, коэффициент эксцесса, коэффициент асимметрии, интервал (размах), минимальное значение, максимальное значение, сумма, число значений, k -е наибольшее и наименьшее значения (для любого заданного значения k ) и уровень значимости для среднего. Установить флажок Итоговая статистика, если нужен полный список характеристик, в противном случае отметить конкретные характеристики, которые должны присутствовать в выходной таблице. Большинство из полученных характеристик, полученных с помощью пакета анализа Описательная статистика можно получить с помощью встроенных статистических формул.
Рис. 7 . 1 Диалоговое окно Описательная статистика
Корреляция используется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (корреляция близка к нулю). В диалоговом окне Корреляция ( REF _Ref12174106 h * MERGEFORMAT Рис. 7.2 ) указывается Входной интервал – ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк.
Рис. 7 . 2 Диалоговое окно Корреляция
Регрессия используется для подбора графика линии регрессии. Параметры диалогового окна Регрессия ( Рис. 7.3 ):
Входной интервал Y – ссылка на диапазон анализируемых зависимых данных (диапазон должен состоять из одного столбца). Входной интервал X – ссылка на диапазон независимых данных, подлежащих анализу. Уровень надежности – установить флажок, чтобы включить в выходной диапазон дополнительный уровень. В соответствующее поле ввести уровень надежности, который будет использован дополнительно к уровню 95%, применяемому по умолчанию. Константа-ноль – установить флажок, чтобы линия регрессии прошла через начало координат. Остатки – установить флажок, чтобы включить остатки в выходной диапазон. Стандартизированные остатки – установить флажок, чтобы включить стандартизированные остатки в выходной диапазон. График остатков – установить флажок, чтобы построить диаграмму остатков для каждой независимой переменной. График подбора – установить флажок, чтобы построить диаграммы наблюдаемых и предсказанных значений для каждой независимой переменной. График нормальной вероятности – установить флажок, чтобы построить диаграмму нормальной вероятности.
Статистический анализ в excel Назначение и возможности пакета анализа
В состав MicrosoftExcelвходит пакет анализа, который позволяет осуществлять статистическую обработку данных в таблицах. В состав этого пакета входят разнообразные статистические методы. Способы применения их всех аналогичны, поэтому мы рассмотрим лишь некоторые из них: экспоненциальное сглаживание, корреляцию, скользящее среднее, регрессию.
Корреляция используется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Корреляционный анализ дает возможность установить ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (корреляция близка к нулю).
Скользящее среднее используется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Процедура может использоваться для прогноза сбыта, инвентаризации и других процессов. Мы спрогнозируем курс доллара США на основе данных за июль 1999 года.
Экспоненциальное сглаживание предназначается для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. Использует константу сглаживания, по величине которой определяет, насколько сильно влияют на прогнозы погрешности в предыдущем прогнозе. Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к сдвигу аргумента для предсказанных значений.
Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. Мы рассмотрим, как влиял на курс ЕВРО по отношению к рублю курс доллара США в июле 1999 года.
Установка пакета анализа.
Если в Microsoft Excel в меню Сервисотсутствует командаАнализ данных, то необходимо установить статистический пакет анализа данных.
Чтобы установить пакет анализа данных
В
Установите флажок Пакет анализа,выберите кнопкуOK.
Вызов пакета анализа
Чтобы запустить пакет анализа:
В меню Сервисвыберите командуАнализ данных.
В списке Инструменты анализавыберите нужную строку.
Корреляция
При выборе строки Корреляцияв диалоговом запросеАнализ данныхпоявляется следующее окно.
Входной интервал. Введите ссылку на ячейки, содержащие анализируемые данные. Ссылка должна состоять как минимум из двух смежных диапазонов данных, организованных в виде столбцов или строк. (Для этого нужно мышью щелкнуть по кнопке 
Группирование. Установите переключатель в положениеПо столбцамилиПо строкамв зависимости от расположения данных во входном диапазоне.
Метки в первой строке/Метки в первом столбце. Установите переключатель в положениеМетки в первой строке, если первая строка во входном диапазоне содержит названия столбцов. Установите переключатель в положениеМетки в первом столбце, если названия строк находятся в первом столбце входного диапазона. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически. (В других видах анализа этот флажок выполняет аналогичную функцию).
Выходной интервал. Введите ссылку на левую верхнюю ячейку выходного диапазона. Поскольку коэффициент корреляции двух наборов данных не зависит от последовательности их обработки, то выходная область занимает только половину предназначенного для нее места. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой.
Новый лист. Установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
Новая книга. Установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
Смотри лист Корреляция в примере.
Вернитесь в текущий документ через Панель задач
результате программа сформирует таблицу с коэффициентами корреляции между выбранными совокупностями.
Регрессионный анализ. Построение статических однофакторных моделей
Практическая работа 1. Регрессионный анализ. Построение статических однофакторных моделей.
Содержательная постановка задачи. Имеется статистическая информация по центральному федеральному округу, которая представлена в таблице1:
Таблица 1. Число гостиниц и число ночевок в гостиницах
Наименование субъекта Федерации
Число гостиниц и аналогичных средств размещения, ед.
Число ночевок в гостиницах и аналогичных средствах размещения, тыс. ночевок
* — на базе данных Федеральной службы государственной статистики.
Пусть ряд наблюдений X — число гостиниц и аналогичных средств размещения, ряд наблюдений Y — число ночевок в гостиницах и аналогичных средствах размещения, тыс.
Часть I.
Построить точечную диаграмму, предварительно отсортировав таблицу; Выдвинуть гипотезу о виде функции зависимости; Рассчитать параметры модели регрессии, построить тренды; Оценить адекватность построенного уравнения по величине достоверности аппроксимации; Рассчитать теоретические значения по модели и построить графики фактических и расчетных данных. Создать отчет в Word по всем пунктам задания, используя экранные копии Excel. Написать вывод о виде функции зависимости, наилучшим образом описывающей модель.
Пример. В исходной таблице произведем сортировку по столбцу С (число гостиниц и аналогичных средств размещения) по возрастанию числа гостиниц.
Рис.1. Сортировка по возрастанию числа гостиниц
Отсортированная таблица представлена на рисунке 2:
Рис.2. Отсортированная таблица по возрастанию числа гостиниц
По отсортированным данным, используя мастер диаграмм, построим точечную диаграмму (диапазон ячеек С1:D19) (Рис.3).
Рис. 3. Диаграмма по отсортированной таблице
После построения диаграммы, вызовем контекстовое меню, щелкнув правой кнопкой мыши по одной из точек диаграммы, и выберем в нем команду Добавить линию тренда…(Рис. 4):
Рис. 4. Вкладка Параметры линии тренда
Во вкладке Параметры линии тренда выберем Линейная и отметим флаги показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Чем R2 ближе к 1, тем удачнее регрессионная модель. На диаграмме появляется линия тренда (Рис. 5).
Рис.5. Диаграмма с линейной линией тренда
Чаще всего выбор производится среди следующих функций:
у = ах + b — линейная функция;
у = ах2 + bх + с — квадратичная (полиномиальная) функция;
у = аln(х) + b — логарифмическая функция;
у = аеbх — экспоненциальная функция;
у = ахb — степенная функция.
Отобразим на диаграмме все возможные тренды (Рис. 6.).
Рис. 6. Диаграмма с построенными линиями тренда
Часть II.
Требуется: рассчитать основные характеристики случайных величин.
Для расчета основных характеристик случайных величин используются следующие функции: СРЗНАЧ() – возвращает среднее арифметическое своих аргументов, КОРЕНЬ() – возвращает значение квадратного корня, а также ДИСП() и КОРРЕЛ().
ДИСП() — Оценивает дисперсию по выборке (Рис.7).
Синтаксис функции: ДИСП(число1;число2; . ).
Число1, число2. — от 1 до 255 числовых аргументов, соответствующих выборке из генеральной совокупности.
Рис. 7. Аргументы функции, оценивающей дисперсию по выборке — Дисп()
КОРРЕЛ() – возвращает коэффициент корреляции между интервалами ячеек «массив1» и «массив2». Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера (Рис. 8).
Синтаксис функции: КОРРЕЛ(массив1;массив2).
Массив1 — это интервал ячеек со значениями, Массив2 — второй интервал ячеек со значениями.
Рис.8. Аргументы функции, возвращающей коэффициент корреляции Коррел()
Получим следующие результаты (Рис. 9):
Рис. 9. Результаты расчетов с использованием математических функций
Можно сделать вывод о том, что линейная зависимость между числом гостиниц и аналогичных средств размещения (ряд X) и числом ночевок в гостиницах и аналогичных средствах размещения (ряд Y) существует, т. к. коэффициент корреляции равен 0,93729 и 
Коэффициент корреляции значим, т. к. расчетный критерий Стъюдента больше табличного критерия: 10,7566 > 2.1190.
Рассчитаем коэффициент корреляции для исходных данных с помощью функции Корреляция пакета Анализ данных.
Вызвать окно Анализ данных можно с помощью команды Анализ данных меню Данные (Рис. 10).
Рис. 10. Анализ данных
Пакет Корреляция позволяет определить коэффициенты корреляции для n-го количества рядов данных. Выбор команды Корреляция вызывает окно Корреляция (Рис. 11).
Рис. 11. Окно Корреляция
Это окно содержит две панели Входные данные и Параметры вывода. Окно Входной интервал: предназначено для ссылки на диапазон, содержащий анализируемые данные. Эта ссылка должна состоять не менее чем из двух смежных диапазонов данных, расположенных по строкам или столбцам. Флаги Группирование: зависят от расположения данных в диапазоне. Флаг Метки в первой строке (Метки в первом столбце) устанавливается в том случае, если входной интервал включал название диапазонов. Если название диапазонов были включены в интервал, а данный флаг не выставлен, после нажатия кнопки Ок, Excel выдаст сообщение об ошибке «Входной интервал содержит нечисловые данные». Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.
Если результаты необходимо поместить на имеющемся листе, то нужно установить переключатель рядом с окном Выходной интервал:, а в самом окне следует ввести ссылку на левую верхнюю ячейку выходного диапазона.
Если установить переключатель рядом с окном Новый рабочий лист:, то в книге откроется новый лист и результаты анализа будут вставлены в него, начиная с ячейки A1. При необходимости в окно можно ввести имя нового листа. По умолчанию имя листа будет соответствовать следующему после последнего имеющегося в книге листа.
Если установить переключатель рядом с окном Новая рабочая книга, то откроется новая книга, и результаты анализа будут вставлены в нее, начиная с ячейки A1 на первом листе в этой книге.
Поскольку коэффициент корреляции двух наборов данных не зависит от последовательности их обработки, то выходная область занимает только половину предназначенного для нее места.
Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой.
Заполняем все необходимые поля окна Корреляция (Рис. 12).
Входной интервал – это данные, по которым необходимо провести корреляционный анализ, в данном случае это исходные данные по числу гостиниц и аналогичных средств размещения и числу ночевок в гостиницах и аналогичных средствах размещения (С2:D19). Строка 1 также указана во входном интервале, но в ней содержатся заголовки столбцов, поэтому ставим флаг Метки в первой строке.
В выходном интервале ставим Новый рабочий лист, в котором будут вынесены результаты расчета.
Рис. 12. Расчет коэффициента корреляции
Полученные данные абсолютно идентичны коэффициентам полученным с помощью функции КОРРЕЛ() (Рис. 13).
Рис. 13. Результаты расчета коэффициента корреляции
Пакет Описательная статистика предназначен для расчета основных статистических показателей. Окно Описательная статистика (Рис. 14) содержит:
Рис.14. Описательная статистика
панель Входные данные, аналогичную панели в окне Корреляция; панель Параметры вывода содержит указание на выходной интервал, аналогичный окну Корреляция; флаг Итоговая статистика обеспечивает вывод в выходной интервал среднего, стандартную ошибку (среднего), медиану, мода, стандартное отклонение, дисперсию выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумму и количество значений; флаг Уровень надежности, установка которого выводит в выходной интервал строку для уровня надежности. Значение, введенное в поле, соответствует требуемому уровню надежности; флаг К-тый наименьший и К-тый наибольший, установка которых выводит в выходной интервал строки для k-го наибольшего и k-го наименьшего значения для каждого диапазона данных. В соответствующем окне необходимо ввести число k. Если k равно 1, эта строка будет содержать минимум или максимум из набора данных.
Далее вызовем функцию Описательная статистика из пакета Анализ данных (Рис. 15).
Рис. 15. Описательная статистика пакета Анализ данных
Выставив все необходимые флаги, нажимаем кнопку Ок, и получаем таблицу описательных статистик (Рис. 16).
Рис. 16. Таблица описательных статистик
Полученные данные совпадают с данными, рассчитанными с помощью математических функций (математическое ожидание по x и по y, дисперсия по x и по y, среднее квадратическое отклонение по x и по y).
Варианты заданий к практической работе 1.
Содержательная постановка задачи. Исходные данные:
построить точечную диаграмму, предварительно отсортировав таблицу; выдвинуть гипотезу о виде функции зависимости; рассчитать параметры модели регрессии, построить тренды; оценить адекватность построенного уравнения по величине достоверности аппроксимации; рассчитать теоретические значения по модели и построить графики фактических и расчетных данных. Создать отчет в Word по всем пунктам задания, используя экранные копии Excel. Написать вывод о виде функции зависимости, наилучшим образом описывающей модель.
Вариант 2. Имеется статистическая информация по Северо-Западному федеральному округу*, которая представлена в таблице:
Число гостиниц и аналогичных средств размещения
Число ночевок в гостиницах и аналогичных средствах размещения, тыс.
Источник
cancel
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Show only
|
Search instead for
Did you mean:
Корреляция входной интервал содержит нечисловые данные что делать
Регистрация на форуме тут, о проблемах пишите сюда — alarforum@yandex.ru, проверяйте папку спам! Обязательно пройдите восстановить пароль
| Поиск по форуму |
| Расширенный поиск |
Случилась такая проблема. Есть долгий цикл получения необходимых мне чисел, в конечном итоге заканчивается тем, что питон на выходе мне выдает значения, нужные мне. Думалось мне, что вот оно счастье, теперь провести небольшую статистику по этим значениям и будет счастье и результаты работы, но не тут-то было. Эксель пишет, что я не могу ничего сделать потому что все значения для него не числовые. Как с этим побороться?
Построить надо мне графики моды, медианы, дисперсии и среднего квадратичного отклонения.
п.с. Я поменял точки на запятые и наоборот уже несколько раз, не помогло.
Вложения
эксель с данными.xlsx (584.2 Кб, 16 просмотров)
| saashaamaar |
| Посмотреть профиль |
| Найти ещё сообщения от saashaamaar |
открыл файл,
поставил курсор в первую ячейку
Ctrl+H
Зайти: .
Заменить на: .
(у меня разделитель целых и дробных — точка)
Заменить все
(75тыс. замен произведено)
Ок
всё! все — теперь числа
А где код?
Можно присвоением массиву с типом variant и последующим выкидыванием в нужный диапазон.
Формат сам меняется на числовой в массиве.
Sub dataconvert()
Set wkRng = ActiveSheet.Cells.Item(1).CurrentRe gion
ReDim arr(wkRng.Rows.Count, wkRng.Columns.Count) As Variant
‘Debug.Print UBound(arr, 1) & » X » & UBound(arr, 2)
arr = wkRng.Value
ActiveSheet.UsedRange.Item(1).Offse t(0, wkRng.Columns.Count + 1).Resize(UBound(arr, 1), UBound(arr, 2)) = arr
End Sub
Если убрать Offset, вставит поверх исходного.
| Miguel Sanchez |
| Посмотреть профиль |
| Найти ещё сообщения от Miguel Sanchez |

Интенсив по Python: Работа с API и фреймворками 24-26 ИЮНЯ 2022. Знаете Python, но хотите расширить свои навыки?
Slurm подготовили для вас особенный продукт! Оставить заявку по ссылке — https://slurm.club/3MeqNEk
Работа с инструментом «Регрессия» в Microsoft Excel
Диалоговое окно «Регрессия». В первое окно «Входной интервал Y» вводим данные объясняемой переменной — у, диапазон должен состоять из одного столбца. Во второе окно «Входной интервал X» вводим данные объясняющих переменных — х. На рис. П.1 представлены у. $С$2:$С$13, х: $В$2:$В$13. Длины интервалов должны быть одинаковы. Если строится уравнение множественной регрессии, то данные объясняющих переменных вводятся в окно «Входной интерват X» соответствующим образом. На рис. П.2 представлены у: $D$2:$D$13, xt—x2: $В2:$С$13. Максималь- ное число независимых объясняющих переменных равно 16.
Рис. П. 1. Задание парной регрессии
Ставим «галочку» в окно «Метки», если в отчете Microsoft Excel требуется знать, к какой из объясняющих переменных относятся результирующие данные.
Если исследователю не требуется константа Ь0, то ставим «галочку» в окно «Константа — ноль». Линия регрессии пройдет через начало координат.
Рис. П.2. Задание множественной регрессии
«Уровень надежности». По умолчанию программа строит уравнение регрессии для доверительной вероятности (уровень надежности) 0,95. Если требуется другая величина, ставим «галочку» в окно «Уровень надежности» и в окно, помеченное символом «%», вводим требуемую величину уровня надежности десятичной дробью.
«Параметры вывода». Указываем, куда вывести результаты регрессионного анализа: на этом листе, как указано на обоих рисунках, на другой рабочий лист или в новую рабочую книгу.
«Остатки». Выбираем то, что требуется исследователю, и ставим «галочку». Можно одновременно пометить несколько окон. Подробная информация дана в справке но инструменту «Регрессия».
Заполнив диалоговое окно «Регрессия», нажимаем кнопку ОК. Программа выводит отчет «Вывод итогов» в виде трех таблиц (рис. П.З, приведено для двух объясняющих переменных).
Приведем описание таблиц (первых двух — в табл. П1.1 и П1.2 соответственно, третьей — в текстовом виде).
Таблица П1.1
Описание первой таблицы
Наименование в отчете
Множественный R
Коэффициент множественной корреляции, индекс корреляции
Коэффициент детерминации, R 2
Скорректированный К 2
Наименование в отчете
Среднее квадратическое отклонение от модели
Рис. П.З. Результаты работы программы
Описание третьей таблицы
Данные первой строки относятся к коэффициенту уравнения регрессии Ь0, данные второй строки — к коэффициенту Ьи третьей — к Ь2 и далее до коэффициента Ьт, но числу объясняющих переменных в уравнении.
Метки, если поставлена галочка в окно «Метки». У-пересечение для коэффициента />0, далее но всем объясняющим переменным.
Значения коэффициентов уравнения регрессии Ь0, Ьь . Ьт.
Стандартная ошибка коэффициента регрессии 5^, 5Л). Sbm.
Статистическая значимость коэффициента регрессии (^-статистика) для а = 0,05 tw . tbm.
P-значение — это значение уровней значимости, соответствующее вычисленным ^статистикам коэффициентов.
Нижние 95% и Верхние 95% — это нижние и верхние границы 95%-ных доверительных интервалов для коэффициентов уравнения регрессии. Если в окно «Уровень надежности» не вводилось другое значение доверительной вероятности, то последние два столбца дублируют предыдущие два столбца. Если в окно «Уровень надежности» было введено другое значение доверительной вероятности у, то последние два столбца содержат значения соответственно нижней и верхней границы у-процентных доверительных интервалов.
Входной интервал содержит нечисловые данные что делать?
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные; 2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш ++.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:- результаты регрессионной статистики, — результаты дисперсионного анализа, — результаты доверительных интервалов, — остатки и графики подбора линии регрессии,
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где – случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Статистический анализ в excel Назначение и возможности пакета анализа
С татистический анализ вExcel
В состав MicrosoftExcelвходит пакет анализа, который позволяетосуществлять статистическую обработкуданных в таблицах. В состав этого пакетавходят разнообразные статистическиеметоды. Способы применения их всеханалогичны, поэтому мы рассмотрим лишьнекоторые из них: экспоненциальноесглаживание, корреляцию, скользящеесреднее, регрессию.
Корреляция используется для количественнойоценки взаимосвязи двух наборов данных,представленных в безразмерном виде.Корреляционный анализ дает возможностьустановить ассоциированы ли наборыданных по величине, то есть, большиезначения из одного набора данных связаныс большими значениями другого набора(положительная корреляция), или, наоборот,малые значения одного набора связаныс большими значениями другого(отрицательная корреляция), или данныедвух диапазонов никак не связаны(корреляция близка к нулю).
Скользящее среднее используется длярасчета значений в прогнозируемомпериоде на основе среднего значенияпеременной для указанного числапредшествующих периодов. Процедураможет использоваться для прогнозасбыта, инвентаризации и других процессов.Мы спрогнозируем курс доллара США наоснове данных за июль 1999 года.
Экспоненциальное сглаживаниепредназначается для предсказаниязначения на основе прогноза дляпредыдущего периода, скорректированногос учетом погрешностей в этом прогнозе.Использует константу сглаживания, повеличине которой определяет, насколькосильно влияют на прогнозы погрешностив предыдущем прогнозе.
Для константысглаживания наиболее подходящимиявляются значения от 0,2 до 0,3. Эти значенияпоказывают, что ошибка текущего прогнозаустановлена на уровне от 20 до 30 процентовошибки предыдущего прогноза. Болеевысокие значения константы ускоряютотклик, но могут привести к непредсказуемымвыбросам.
Низкие значения константымогут привести к сдвигу аргумента дляпредсказанных значений.
Линейный регрессионный анализ заключаетсяв подборе графика для набора наблюденийс помощью метода наименьших квадратов.Регрессия используется для анализавоздействия на отдельную зависимуюпеременную значений одной или болеенезависимых переменных. Мы рассмотрим,как влиял на курс ЕВРО по отношению крублю курс доллара США в июле 1999 года.
Установка пакета анализа
Если в Microsoft Excel в меню Сервисотсутствует командаАнализ данных,то необходимо установить статистическийпакет анализа данных.
Чтобы установить пакет анализа данных
ВменюСервисвыберите командуНадстройки. Если в списке надстроек нет пакета анализа данных, нажмите кнопкуОбзори укажите диск, папку и имя файла для надстройки пакет анализа, Analys32.xll (как правило, папка LibraryAnalysis) или запустите программу Setup, чтобы установить эту надстройку.
Установите флажок Пакет анализа,выберите кнопкуOK.
Вызов пакета анализа
Чтобы запустить пакет анализа:
В меню Сервисвыберите командуАнализ данных.
В списке Инструменты анализавыберите нужную строку.
Корреляция
При выборе строки Корреляциявдиалоговом запросеАнализ данныхпоявляется следующее окно.
Входной интервал. Введите ссылкуна ячейки, содержащие анализируемыеданные. Ссылка должна состоять какминимум из двух смежных диапазоновданных, организованных в виде столбцовили строк. (Для этого нужно мышью щелкнутьпо кнопкев правом конце строки, установитьмышь в верхний правый угол диапазонаанализируемых данных и, удерживаянажатой левую кнопку мыши, отбуксироватьмышь в левый нижний угол диапазона,нажать клавишуEnter).
Группирование. Установите переключательв положениеПо столбцамилиПострокамв зависимости от расположенияданных во входном диапазоне.
Метки в первой строке/Метки в первомстолбце. Установите переключатель вположениеМетки в первой строке,если первая строка во входном диапазонесодержит названия столбцов. Установитепереключатель в положениеМетки впервом столбце, если названия строкнаходятся в первом столбце входногодиапазона. Если входной диапазон несодержит меток, то необходимые заголовкив выходном диапазоне будут созданыавтоматически. (В других видах анализаэтот флажок выполняет аналогичнуюфункцию).
Выходной интервал. Введите ссылкуна левую верхнюю ячейку выходногодиапазона. Поскольку коэффициенткорреляции двух наборов данных независит от последовательности ихобработки, то выходная область занимаеттолько половину предназначенного длянее места. Ячейки выходного диапазона,имеющие совпадающие координаты строки столбцов, содержат значение 1, так каккаждая строка или столбец во входномдиапазоне полностью коррелирует с самимсобой.
Новый лист. Установите переключатель,чтобы открыть новый лист в книге ивставить результаты анализа, начинаяс ячейки A1. Если в этом есть необходимость,введите имя нового листа в поле,расположенном напротив соответствующегоположения переключателя.
Новая книга. Установите переключатель,чтобы открыть новую книгу и вставитьрезультаты анализа в ячейку A1 на первомлисте в этой книге.
Смотри лист Корреляция в примере.
Вернитесь в текущий документ через Панель задач
результате программа сформируеттаблицу с коэффициентами корреляциимежду выбранными совокупностями.
Использование электронных таблиц Excel для вычисления выборочных характеристик данных — КТНО
Математическая статистика подразделяется на две основные области:описательную и аналитическую статистику. Описательная статистика охватываетметоды описания статистических данных, представления их в форме таблиц,распределений.
Аналитическая статистика или теория статистических выводовориентирована на обработку данных, полученных в ходе эксперимента, с цельюформулировки выводов, имеющих прикладное значение для самых различных областейчеловеческой деятельности.
1. Характеристика пакета Excel
Пакет Excel оснащенсредствами статистической обработки данных. И хотя Excel существенно уступает специализированным статистическим пакетамобработки данных, тем не менее этот раздел математики представлен в Excel наиболее полно. В него включены основные,наиболее часто используемые статистические процедуры: средства описательнойстатистики, критерии различия, корреляционные и другие методы, позволяющиепроводить необходимый статистический анализ экономических, психологических,педагогических и медико-биологических типов данных.
Каждая единица информации занимает свою собственную ячейку(клетку) в создаваемой рабочей таблице. В каждой рабочей таблице 256 столбцов(из которых в новой рабочей таблице на экране видны, как правило, только первые10 или 11 (от А до J или К) и 65 536 строк (из которых обычно видны толькопервые 15-20). Каждая новая рабочая книга содержит три чистых листа рабочихтаблиц.
Вся помещаемая в электронную таблицу информация хранится в отдельныхклетках рабочей таблицы. Но ввести информацию можно только в текущую клетку. Спомощью адреса в строке формул и табличного курсора Excel указывает, какая изклеток рабочей таблицы является текущей. В основе системы адресации клетокрабочей таблицы лежит комбинация буквы(или букв) столбца и номера строки, например A2, B12.
При рассмотрении применения методов обработки статистическихданных в данной лабораторной работе ограничимся только простейшими и наиболеечасто описательными статистиками, реализованными в мастере функций Excel.
2 Использование специальных функций
В мастере функций Excel имеется рядспециальных функций, предназначенных для вычисления выборочных характеристик.
Функция СРЗНАЧ вычисляет среднее арифметическое изнескольких массивов (аргументов) чисел. Аргументы число1, число2, … — этоот 1 до 30 массивов для которых вычисляется среднее.
Функция МЕДИАНА позволяет получать медиану заданнойвыборки. Медиана — это элемент выборки, число элементов выборки со значениямибольше которого и меньше которого равно.
Функция МОДА вычисляет наиболее часто встречающеесязначение в выборке.
Функция ДИСП позволяет оценить дисперсию повыборочным данным.
Функция СТАНДОТКЛОН вычисляет стандартное отклонение.
Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочнымданным.
Функция СКОС позволяет оценить асимметриювыборочного распределения.
Функция КВАРТИЛЬ вычисляет квартилираспределения. Функция имеет формат КВАРТИЛЬ(массив, значение), где массив– интервал ячеек, содержащих значения СВ; значение определяет какаяквартиль должна быть найдена (0 – минимальное значение, 1 – нижняя квартиль, 2– медиана, 3 – верхняя квартиль, 4 – максимальное значение распределения).
Пример 1. Провести статистический анализметодом описательной статистики доходов населения в регионе 1 и регионе 2.
1. Наблюдение посещаемостичетырех внеклассных мероприятий в экспериментальном (20 человек) и контрольном(30 человек) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23,10, 28. Требуется найти среднее значение, стандартное отклонение, медиану иквартили этих данных.
2. Найти среднее значение,медиану, стандартное отклонение и квартили результатов бега на дистанцию 100 м у группы студентов (с):12,8; 13,2; 13,0; 12,9; 13,5; 13,1.
3. Определите верхнюю и нижнююквартиль, выборочную асимметрию и эксцесс для данных измерений роста группстуденток: 164, 160, 157, 166, 162, 160, 161, 159, 160, 163, 170, 171.
4. Найти наиболее популярный туристический маршрут из четырехреализуемых фирмой, если за неделю последовательно были реализованы следующиемаршруты: 1, 3, 3, 2, 1, 1, 4, 4, 2, 4, 1, 3, 2, 4, 1, 4, 4, 3, 1, 2, 3, 4, 1,1, 3.
3. Использование инструмента Пакет анализа
В пакете Excel помимо мастерафункций имеется набор более мощных инструментов для работы с несколькимивыборками и углубленного анализа данных, называемый Пакет анализа, которыйможет быть использован для решения задач статистической обработки выборочныхданных.
Для установки пакета Анализданных в Excel сделайте следующее:
— в меню Сервис выберите команду Надстройки;
— в появившемся списке установите флажок Пакетанализа.
Для использования статистического пакета анализа данных необходимо:
- указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;
- в раскрывающемся списке выбрать команду Анализданных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);
- выбрать строку Описательнаястатистика и нажать кнопку Оk
- в появившемся диалоговом окне указать входной интервал, то есть ввести ссылки на ячейки, содержащие анализируемые данные;
- указать выходной интервал, то есть ввести ссылку на ячейку, в которую будут выведены результаты анализа;
- в разделе Группирование переключатель установить в положение по столбцам или по строкам;
- установить флажок в поле Итоговая статистика и нажать Ок.
Задание для самостоятельной работы
1. В рабочей зоне производились замеры концентрации вредноговещества. Получен ряд значений (в мг./м3):12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16. Необходимо определитьосновные выборочные характеристики.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек. Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось.Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Функция СЧЁТЕСЛИ и подсчет количества значения ячейки в Excel
Функция СЧЁТЕСЛИ в Excel используется для подсчета количества ячеек в рассматриваемом диапазоне, содержащиеся данные в которых соответствуют критерию, переданному в качестве второго аргумента данной функции, и возвращает соответствующее числовое значение.
Функция СЧЁТЕСЛИ может быть использована для анализа числовых значений, текстовых строк, дат и данных другого типа. С ее помощью можно определить количество неповторяющихся значений в диапазоне ячеек, а также число ячеек с данными, которые совпадают с указанным критерием лишь частично. Например, таблица Excel содержит столбец с ФИО клиентов. Для определения количества клиентов-однофамильцев с фамилией Иванов можно ввести функцию =СЧЁТЕСЛИ(A1:A300;”*Иванов*”). Символ «*» указывает на любое количество любых символов до и после подстроки «Иванов».
Пример 1. В таблице Excel содержатся данные о продажах товаров в магазине бытовой техники за день. Определить, какую часть от проданной продукции составляет техника фирмы Samsung.
Вид исходной таблицы данных:
Для расчета используем формулу:
- C3:C17 – диапазон ячеек, содержащих названия фирм проданной техники;
- «Samsung» – критерий поиска (точное совпадение);
- A17 – ячейка, хранящая номер последней продажи, соответствующий общему числу продаж.
Доля проданной продукции техники фирмы Samsung в процентах составляет – 40%.
Пример 2. По итогам сдачи экзаменов необходимо составить таблицу, в которой содержатся данные о количестве студентов, сдавших предмет на 5, 4, 3 балла соответственно, а также тех, кто не сдал предмет.
Вид исходной таблицы:
Предварительно выделим ячейки E2:E5, введем приведенную ниже формулу:
- B3:B19 – диапазон ячеек с оценками за экзамен;
- D2:D5 – диапазон ячеек, содержащих критерии для подсчета числа совпадений.
В результате получим таблицу:
Статистический анализ посещаемости с помощью функции СЧЁТЕСЛИ в Excel
Пример 3. В таблице Excel хранятся данные о просмотрах страниц сайта за день пользователями. Определить число пользователей сайта за день, а также сколько раз за день на сайт заходили пользователи с логинами default и user_1.
Вид исходной таблицы:
Поскольку каждый пользователь имеет свой уникальный идентификатор в базе данных (Id), выполним расчет числа пользователей сайта за день по следующей формуле массива и для ее вычислений нажмем комбинацию клавиш Ctrl+Shift+Enter:
Выражение 1/СЧЁТЕСЛИ(A3:A20;A3:A20) возвращает массив дробных чисел 1/количество_вхождений, например, для пользователя с ником sam это значение равно 0,25 (4 вхождения). Общая сумма таких значений, вычисляемая функцией СУММ, соответствует количеству уникальных вхождений, то есть, числу пользователей на сайте. Полученное значение:
Для определения количества просмотренных страниц пользователями default и user_1 запишем формулу:
В результате расчета получим:
Особенности использования функции СЧЁТЕСЛИ в Excel
Функция имеет следующую синтаксическую запись:
- диапазон – обязательный аргумент, принимающий ссылку на одну либо несколько ячеек, в которых требуется определить число совпадений с указанным критерием.
- критерий – условие, согласно которому выполняется расчет количества совпадений в рассматриваемом диапазоне. Условием могут являться логическое выражение, числовое значение, текстовая строка, значение типа Дата, ссылка на ячейку.
- При подсчете числа вхождений в диапазон в соответствии с двумя различными условиями, диапазон ячеек можно рассматривать как множество, содержащее два и более непересекающихся подмножеств. Например, в таблице «Мебель» необходимо найти количество столов и стульев. Для вычислений используем выражение =СЧЁТЕСЛИ(B3:B200;»*стол*»)+СЧЁТЕСЛИ(B3:B200;»*стул*»).
- Если в качестве критерия указана текстовая строка, следует учитывать, что регистр символов не имеет значения. Например, функция СЧЁТЕСЛИ(A1:A2;»Петров») вернет значение 2, если в ячейках A1 и A2 записаны строки «петров» и «Петров» соответственно.
- Если в качестве аргумента критерий передана ссылка на пустую ячейку или пустая строка «», результат вычисления для любого диапазона ячеек будет числовое значение 0 (нуль).
- Функция может быть использована в качестве формулы массива, если требуется выполнить расчет числа ячеек с данными, удовлетворяющим сразу нескольким критериям. Данная особенность будет рассмотрена в одном из примеров.
- Рассматриваемая функция может быть использована для определения количества совпадений как по одному, так и сразу по нескольким критериям поиска. В последнем случае используют две и более функции СЧЁТЕСЛИ, возвращаемые результаты которых складывают или вычитают. Например, в ячейках A1:A10 хранится последовательность значений от 1 до 10. Для расчета количества ячеек с числами больше 3 и менее 8 необходимо выполнить следующие действия:
Скачать примеры функции СЧЁТЕСЛИ для подсчета ячеек в Excel
- записать первую функцию СЧЁТЕСЛИ с критерием «>3»;
- записать вторую функцию с критерием «>=8»;
- определить разницу между возвращаемыми значениями =СЧЁТЕСЛИ(A1:10;»>3″)-СЧЁТЕСЛИ(A1:A10;»>=8″). То есть, вычесть из множества (3;+∞) подмножество [8;+∞).
Как правильно вычислить среднее значение?
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
Давайте обратимся к классическому примеру со средней зарплатой.
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
- x – среднее арифметическое;
- xn – конкретное значение;
- n – количество значений.
- Хорошо работает при нормальном распределении значений в выборке;
- Легко вычислить;
- Интуитивно понятно.
- Не дает реального представления о распределении значений;
- Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
- M0 – мода;
- x0 – нижняя граница интервала, который содержит моду;
- n – величина интервала;
- fm– частота (сколько раз в ряду встречается то или иное значение);
- fm-1 – частота интервала предшествующего модальному;
- fm+1 – частота интервала следующего за модальным.
- Прекрасно подходит для получения представления об общественном мнении;
- Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
- Проста для понимания.
- Моды может просто не быть (нет повторов);
- Мод может быть несколько (многомодальное распределение).
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
- Me – медиана;
- x0 – нижняя граница интервала, который содержит медиану;
- h – величина интервала;
- f i – частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 – сумма частот интервалов предшествующих медианному;
- fm – число значений в медианном интервале (его частота).
- Дает самую реалистичную и репрезентативную оценку;
- Устойчива к выбросам.
- Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
- СРЗНАЧ(число1;[число2];…) — функция для определения среднего арифметического;
- МОДА.ОДН(число1;[число2];…) — функция моды (в более старых версиях Excel использовалась МОДА(число1;[число2];…));
- МЕДИАНА(число1;[число2];…) — функция для поиска медианы.
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.
И чтобы ее использовать достаточно написать вот такой запрос:
/* Здесь и далее salary — столбец с зарплатами, а employees — таблица сотрудников в нашей базе данных */ SELECT AVG(salary) AS ‘Средняя зарплата’ FROM employees
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */ SELECT TOP(1) WITH TIES salary AS ‘Мода зарплаты’ FROM employees GROUP BY salary ORDER BY COUNT(*) DESC
Вычисляем медиану на SQL
Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.
Выглядит все это так:
/* В данном случае процентиль 0.5 и будет являться медианой */ SELECT TOP(1) PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY salary) OVER() AS ‘Медианная зарплата’ FROM employees
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при ании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Полезные ссылки:
Как сделать проверку данных в Excel: примеры формул, контроль достоверности информации, определение правил, настройка простого выпадающего меню
При заполнении таблиц в Экселе вручную приходится вводить очень много данных, что может привести к появлению множества опечаток и ошибок. Некоторые такие ошибки может исключить проверка данных в Excel при вводе, что мы далее и рассмотрим.
Сразу стоит отметить, что проверка вводимых данных в Excel будет работать только при вводе этих данных с клавиатуры. При вставке информации из буфера обмена или другого источника проверка не выполняется. Для уже введенных значений все-же можно произвести проверку, что приведет к обведению неверных данных красным овалом, но об этом далее.
Чтобы сделать проверку данных в Excel для определенных ячеек, их необходимо выделить, перейти на вкладку «Данные», и найти в разделе «Работа с данными» меню «Проверка данных». При нажатии на стрелочку справа от данного пункта появляется три пункта меню, из которых нам нужен самый первый «Проверка данных…».
В появившемся окошке «Проверка вводимых значений» настраивается проверка. На вкладке «Параметры» выбирается из списка тип данных, которые будут проверяться и вводиться в выделенный нами диапазон ячеек. Для примера выберем «Целое число».
После выбора типа данных становится возможным выбор условия соответствия вводимого значения в графе «Значение:». Выберем для примера «Между»
- Далее в графах «Минимум:» и «Максимум:» необходимо указать значения, или указать на ячейки с данными значениями, нажав на соответствующий значок справа от каждой графы ввода.
- На следующей вкладке «Сообщение для ввода» можно указать заголовок и само сообщение подсказку, которое будет высвечиваться при активации ячейки с проверкой вводимых данных.
На вкладке «Сообщение об ошибке» можно указать заголовок и само сообщение, появляющееся при ошибочном вводе данных, а также действие, которое при этом будет производится. На вкладке «Вид:» доступно три варианта.
«Останов» предотвращает ввод недопустимых данных и предлагает повторить попытку. «Предупреждение» выдает сообщение об ошибке, но дает возможность продолжить ввод недопустимого значения.
«Сообщение» просто проинформирует о недопустимом введенном значении.
- Сообщение подсказка.
- Вид «Останов».
- Вид «Предупреждение».
- Вид «Сообщение».
Для проверки уже введенных или вставленных через буфер обмена значений, можно выбрать пункт меню «Обвести неверные данные», после чего неудовлетворяющие условию значения будут обведены красным овалом. После ввода правильного значения овал автоматически исчезает.
Руководство по проверке данных Excel
Проверка данных — это функция в Excel, используемая для контроля того, что пользователь может ввести в ячейку. Например, вы можете использовать проверку данных, чтобы убедиться, что:
- значение является числом от 1 до 6
- дата произойдет в следующие 30 дней
- текстовая запись содержит менее 25 символов
Проверка данных может просто отображать сообщение пользователю с информацией, что разрешено, как показано ниже:
Сообщение отображается автоматически при выборе ячейки
Проверка данных также может остановить неправильный ввод данных пользователем. Например, если код сотрудника не проходит проверку, вы можете увидеть следующее сообщение:
Пример сообщения об ошибке
Кроме того, проверка данных может использоваться для предоставления пользователю определенного выбора в раскрывающемся меню:
Пример раскрывающегося меню проверки данных
Это очень удобно, так как можно дать пользователю именно те значения, которые уже соответствуют требованиям.
Контроль достоверности данных
Проверка данных осуществляется с помощью правил, определенных в пользовательском интерфейсе Excel на вкладке «Данные» на ленте.
Элементы управления проверкой данных на вкладке ДАННЫЕ
Важное ограничение
Важно понимать, что проверку данных можно легко обойти. Если пользователь копирует данные из ячейки без проверки в ячейку с проверкой данных, проверка уничтожается (или заменяется). Проверка данных — это хороший способ помочь пользователям, сообщив им критерии ввода, но он не дает гарантированную защиту от ошибок.
Определение правил проверки данных
Проверка данных определяется в окне с 3 вкладками: Параметры, Сообщение для ввода и Сообщение об ошибке:
Окно проверки данных имеет три основные вкладки
На вкладке Параметры вы можете ввести критерии проверки. Существует ряд встроенных правил проверки с различными параметрами, также можно выбрать «Другой» и использовать собственную формулу для проверки ввода, как показано ниже:
Пример вкладки настроек проверки данных
Вкладка «Сообщение для ввода» определяет сообщение, отображаемое при выборе ячейки с правилами проверки. Оно не является обязательным.
Если сообщение не установлено, оно не отображается, когда пользователь выбирает ячейку с примененной проверкой данных.
Входное сообщение не влияет на то, что пользователь может ввести — оно просто отображает сообщение, чтобы сообщить пользователю, что разрешено или ожидается.
Вкладка настройки сообщения проверки данных
Вкладка «Сообщение об ошибке» определяет, как выполняется проверка. Например, когда вид установлен на «Останов», неверные данные вызывают окно с сообщением, и ввод не разрешен.
Вкладка предупреждения об ошибке проверки данных
Пользователь видит сообщение, подобное этому:
Пример сообщения об ошибке проверки данных
Когда в поле «Вид» установлено значение «Сообщение» или «Предупреждение», изменяется значок, отображаемый с пользовательским сообщением. Пользователь может игнорировать сообщение и вводить значения, которые не проходят проверку. Ниже обобщено поведение каждого вида предупреждения об ошибке.
Не позволяет пользователям вводить недопустимые данные в ячейку. Пользователи могут повторить попытку, но должны ввести значение, которое проходит проверку данных. В окне предупреждения «Останов» есть три опции: «Повторить», «Отмена» и «Справка».
Предупреждает пользователей о том, что данные неверны. Предупреждение ничего не делает, чтобы остановить ввод неверных данных. В окне «Предупреждение» есть три параметра: «Да» (для принятия недействительных данных), «Нет» (для редактирования недействительных данных), «Отмена» (для удаления недействительных данных) и «Справка».
Сообщает пользователям, что данные являются недействительными. Это сообщение не делает ничего, чтобы остановить ввод неверных данных. Информационное окно имеет 3 кнопки: «ОК», чтобы принять недействительные данные, «Отмена», чтобы удалить их и «Справка».
Параметры проверки данных
При создании правила проверки данных доступно восемь параметров:
Любое значение — проверка не выполняется. Примечание: если проверка данных ранее применялась с установленным входным сообщением, сообщение все равно будет отображаться при выборе ячейки, даже если выбрано любое значение.
Целое число — разрешены только целые числа. Как только опция целого числа выбрана, другие опции становятся доступными для дальнейшего ограничения ввода. Например, вам может потребоваться целое число от 1 до 10.
Действительное — работает как опция целого числа, но допускает десятичные значения. Например, если для параметра «Действительное» задано значение от 0 до 3, допустимы все значения, такие как 0,5 и 2,5.
Список — разрешены только значения из предварительно определенного списка. Значения представляются пользователю как выпадающее меню. Допустимые значения могут быть жестко заданы непосредственно на вкладке «Параметры» или указаны в виде диапазона на рабочем листе.
Дата — разрешены только даты. Например, вам может потребоваться дата между 1 января 2018 года и 31 декабря 2021 года или дата после 1 июня 2018 года.
Время — разрешено только время. Например, вы можете указать время между 9:00 и 17:00 или разрешить время только после 12:00.
Длина текста — проверяет ввод на основе количества символов или цифр. Например, вам может потребоваться код из 5 цифр.
Другой — проверяет ввод с использованием пользовательской формулы. Другими словами, вы можете написать собственную формулу для проверки ввода. Пользовательские формулы значительно расширяют возможности проверки данных. Например, вы можете использовать формулу, чтобы обеспечить значение в верхнем регистре, или значение, которое содержит «АБВ».
На вкладке параметров также есть два флажка:
Игнорировать пустые ячейки — говорит Excel не проверять ячейки, которые не содержат значений. На практике этот параметр влияет только на команду «Обвести неверные данные». Когда эта опция включена, пустые ячейки не обведены, даже если они не прошли проверку.
Распространить изменения на другие ячейки с тем же условием — этот параметр обновит проверку, примененную к другим ячейкам, когда она будет соответствовать (оригинальной) проверке редактируемых ячеек.
Простое выпадающее меню
Вы можете предоставить пользователю раскрывающееся меню опций, жестко закодировав значения в поле настроек или выбрав диапазон на листе. Например, чтобы ограничить записи действиями «ПРИНЯТ», «В ОБРАБОТКЕ» или «ОТГРУЖЕН», вы можете ввести эти значения через точку с запятой:
Раскрывающееся меню проверки данных с жестко заданными значениями
При применении к ячейке на рабочем листе раскрывающееся меню работает следующим образом:
Содержание
- Инструментарий Microsoft Excel 2000 для решения множественной регрессионной задачи
- Числовые характеристики результатов наблюдения
- Формирование выборки
- Корреляционный анализ
- Регрессионный анализ
- Ряды динамики
- Список рекомендуемой литературы
Инструментарий Microsoft Excel 2000 для решения множественной регрессионной задачи
В русифицированной версии EXCEL 97 для корреляционно-регрессионного анализа используются средства специального статистического модуля. Microsoft заказывала разработку этого модуля фирме, специализирующейся на программном обеспечении математико-статистических задач. Модуль включает в себя два вида средств математико-статистического анализа: функции и инструменты. Мы отдаем предпочтение сложным инструментам, обеспечивающим более высокий уровень автоматизации расчетов, комплексности, графического моделирования и организации результатов. Однако некоторые пользователи в определенных случаях вполне обоснованно могут предпочесть функции.
Множественный корреляционно-регрессионный анализ в основном ориентирован на средства дополнительного пакета Анализ данных. Активизация команды Сервис Анализ данных открывает окно Инструменты анализа, предоставляющее 19 статистических инструментальных средств. Среди них — Корреляция и Регрессия, непосредственно и эффективно поддерживающие простой и множественный корреляционно-регрессионный анализ
Эти сложные инструменты доступны в том случае, если они предварительно загружены через команду Сервис / Надстройки. В открывшемся окне дополнений следует пометить флажок слева от позиции пакет анализа, и затем щелкнуть по кнопке ОК. После повторного обращения к команде Сервис, позиция Анализ данных появится в конце меню. Если же команда Анализ данных и в этом случае отсутствует в меню Сервис, то необходимо запустить программу установки Microsoft Excel. После установки пакета анализа его необходимо активизировать с помощью команды Надстройки.
С помощью инструмента Корреляция, можно получить корреляционную матрицу парных коэффициентов за один прием. Для этого, после выбора Сервис/Анализ данных/Корреляция, следует определить в качестве входного все поле имеющихся исходных данных, корреляционные связи которых изучают. Затем следует уточнить с помощью флажков, по столбцам или по строкам размещены переменные. Если поле содержит заголовочную строку (или столбец), то в диалоге активизируют графический флажок Метки (Labels). После выбора графической кнопки выполнения (ОК), корреляционная матрица автоматически выводится на новый лист той же электронной таблицы, начиная с клетки А1. Если матрицу желают вывести на какой-либо конкретный лист и начиная с клетки, определяемой пользователем, то делают соответствующие установки в окне «Выходной интервал» диалогового окна инструмента Корреляция.
Вид корреляционной матрицы, полученной в результате определения входного поля представлен в таблице:
| А | B | C | D | E |
| Х1 | Х2 | Х3 | Х4 | |
| X1 | ||||
| Х2 | k12 | |||
| Х3 | k13 | k21 | ||
| Х4 | k14 | k22 | k34 |
Можно осуществить преобразование корреляционной матрицы копированием в нее формулы для диагностики связей по модулю коэффициента корреляции.
Вспомогательная диагностирующая формула.
Поделиться с друзьями:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.008 сек. —>
Источник
Числовые характеристики результатов наблюдения
Следующим этапом статистического анализа данных после построения вариационного ряда является характеристика отдельных свойств распределения данных наблюдения. С этой целью в статистике используются специальные числовые параметры, найденные по результатам наблюдения и отражающие в сжатом виде основные, существенные черты распределения данных. Эти числовые параметры называются эмпирическими числовыми характеристиками. Наиболее важными числовыми характеристиками являются характеристики положения, вариации, асимметрии и эксцесса.
Для характеристики положения используются показатели центра распределения данных наблюдения– средняя арифметическая, мода и медиана.
Средняя арифметическая для дискретного ряда распределения рассчитывается по формуле:


– частота повторения данного варианта.
В интервальном вариационном ряду средняя арифметическая определяется по формуле:


Мода распределения– это наиболее часто встречающееся значение признака в совокупности. В дискретном ряду определение моды не требует специальных расчётов. Мода соответствует варианту с наибольшей частотой. В интервальном вариационном ряду в отличие от дискретного ряда определение моды требует определённых расчётов на основе специальной формулы.
Модальный интервал (то есть содержащий моду) при интервальном распределении с равными интервалами определяется по наибольшей частоте, а с неравными интервалами– по наибольшей плотности. В первом случае мода рассчитывается по следующей формуле:
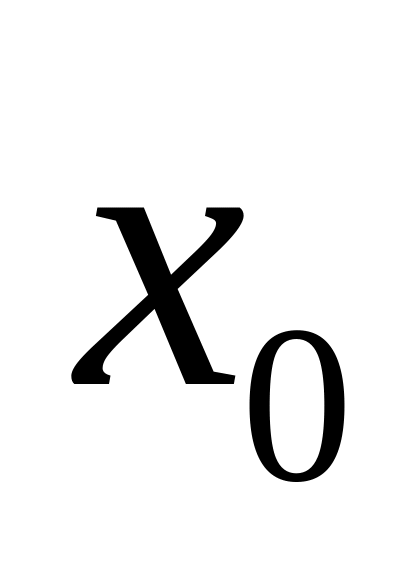
– величина модального интервала;

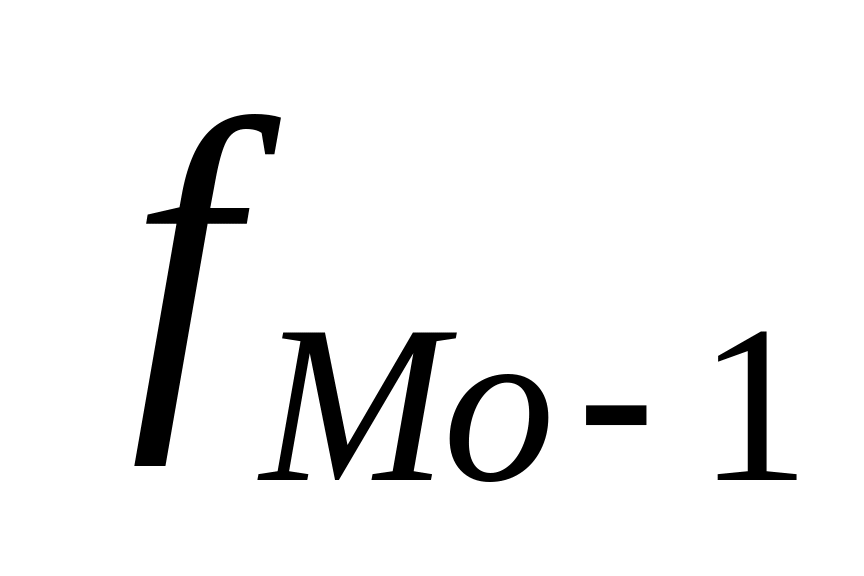

Во втором случае в формуле моды вместо частот 

Медиана – это значение признака, расположенное в середине (в центре) ранжированного ряда. Медиана делит совокупность на две равные части– со значениями признака меньше медианы и со значениями признака больше медианы.
В дискретном ряду для вычисления медианного значения признака сначала находят его порядковый номер:

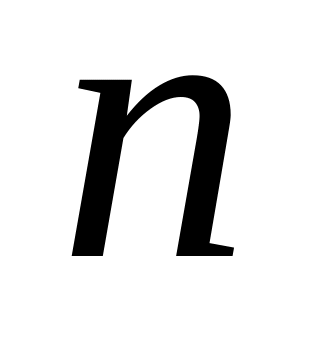
Полученное значение указывает, что середина приходится на данный номер единицы совокупности. Необходимо определить, к какой группе относится единица с этим порядковым номером. Это можно сделать, рассчитав накопленные частоты.
В интервальном вариационном ряду медиана определяется по формуле:
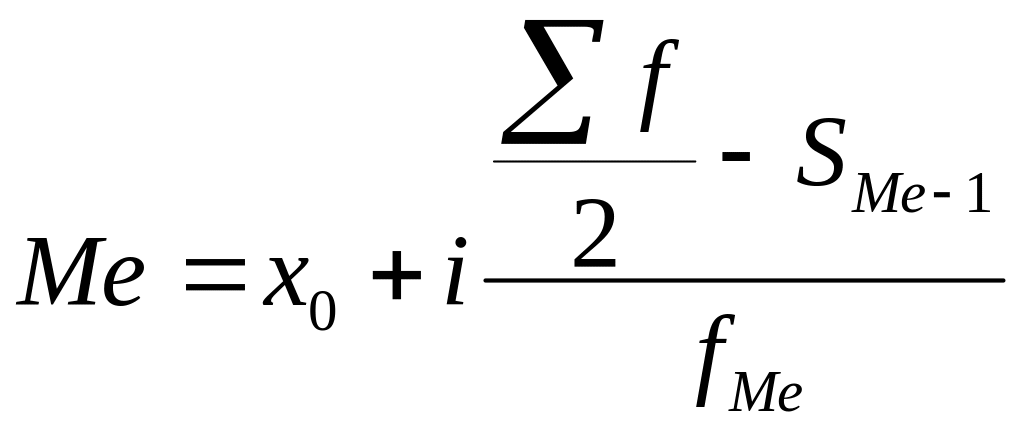
– нижняя граница медианного интервала;
– величина медианного интервала;



Медианным является интервал, в котором сумма накопленных частот равна или превышает полусумму частот ряда.
Основными характеристики вариации признака являются дисперсия, среднее квадратическое (стандартное) отклонение и коэффициент вариации. Они характеризуют степень рассеивания данных наблюдения относительно центра распределения.
Дисперсия рассчитывается по формуле:

Среднее квадратическое (стандартное) отклонение равно корню квадратному из дисперсии.
Коэффициент вариации равен:

Для оценки степени отклонения распределения исследуемой величины от нормального распределения используется коэффициент асимметрии, основанный на определении центрального момента третьего порядка 

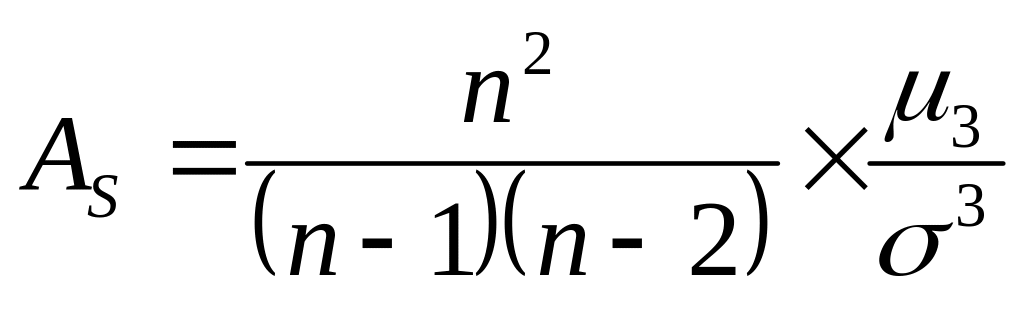
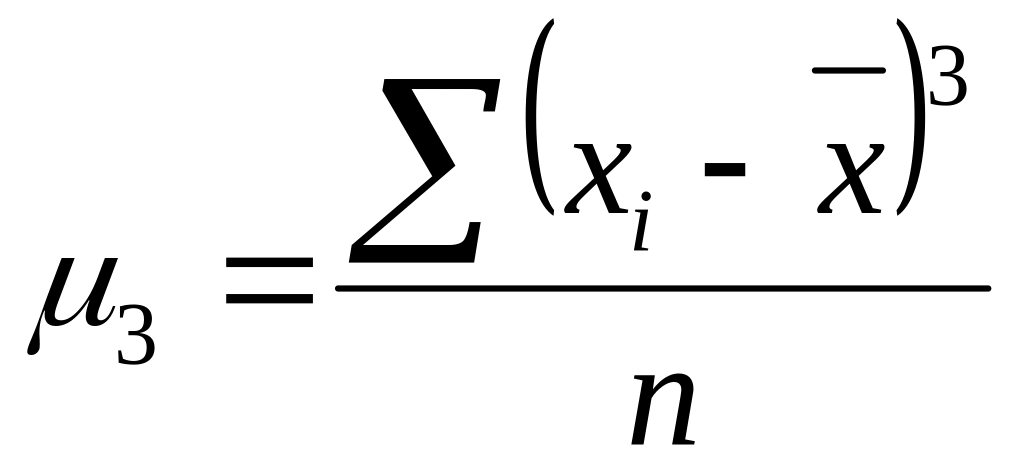
Стандартизированный коэффициент асимметрии 
Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения, имеющей куполообразную форму.
Наиболее точным является коэффициент эксцесса, основанный на использовании центрального момента четвёртого порядка: 

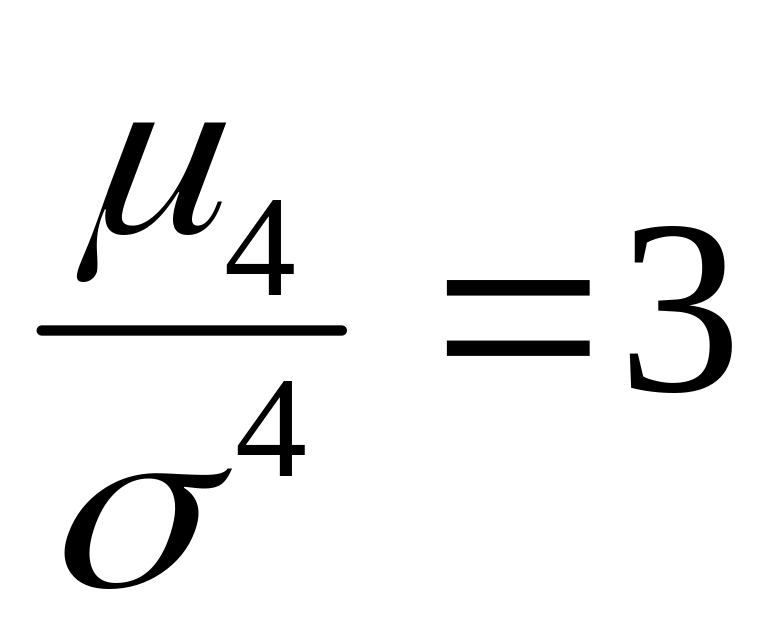
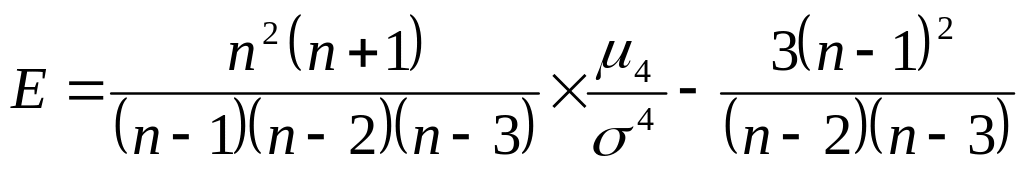

Стандартизированный выборочный коэффициент эксцесса 
В Excel числовые характеристики вычисляются с помощью процедуры Описательная статистика, входящей в Пакет анализа, и соответствующих встроенных статистических функций СРЗНАЧ, МЕДИАНА, МОДА, ДИСП, ДИСПР, СТАНДОТКЛОН, СТАНДОТКЛОНП, СРОТКЛ, КВАДРОТКЛ, СКОС и ЭКСЦЕСС.
Для доступа к процедуре Описательная статистика необходимо:
В меню Сервис выделить строку Анализ данных.
В открывшемся окне Анализ данных выделить процедуру Описательная статистика и щёлкнуть на кнопке ОК. На экране появится диалоговое окно Описательная статистика, которое содержит следующие элементы управления:
поле ввода Входной интервал. В это поле вводится ссылка на диапазон ячеек (входной диапазон), содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом или группой смежных столбцов (строкой или группой смежных строк). Если входной диапазон представляет собой группу столбцов (строк), то процедура воспринимает каждый столбец (строку) как отдельную совокупность;
флажок Итоговая статистика. Если этот флажок установлен, процедура вычисляет и помещает в таблицу результатов решения следующие числовые характеристики: среднюю, стандартную ошибку средней, медиану, моду, стандартное отклонение, дисперсию, эксцесс, асимметрию, размах вариации, минимальное и максимальное значение изучаемого признака, сумму всех значений признака и объём совокупности. Если совокупность не имеет повторяющихся значений признака, в строке Мода появляется сообщение # Н/Д!– неопределённые данные;
флажок Уровень надёжности. Флажок устанавливается в том случае, когда необходимо вычислить доверительный интервал для средней, соответствующий заданной доверительной вероятности. При этом справа от флажка открывается поле для ввода доверительной вероятности, выраженной в процентах. Если этот флажок установлен, то в последней строке таблицы результатов решения появляется число, равное половине длины доверительного интервала;
флажки К-й наименьший/К-й наибольший. Если эти флажки установлены. то в таблице результатов решения появляются -й и 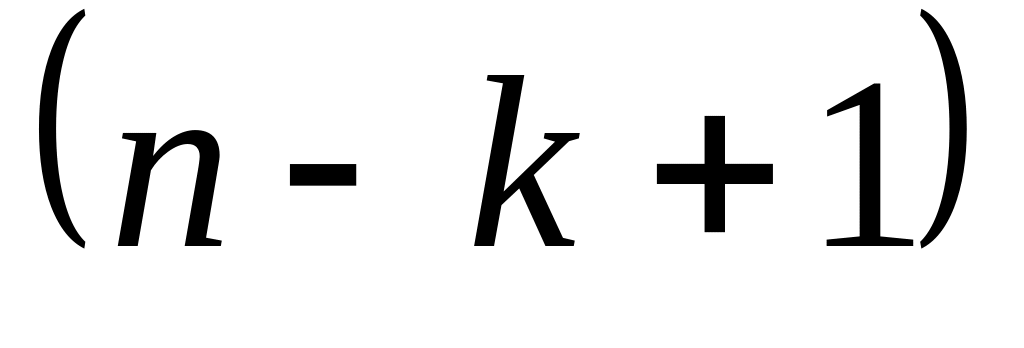
Назначение переключателей Группирование по столбцам/по строкам, флажка Метки в первой строке/Метки в первом столбце и группы переключателей Выходной интервал/Новый рабочий лист/Новая книга рассмотрено на стр. 8-9.
Результаты решения выводятся на экран в виде набора таблиц– по одной таблице на каждый столбец входного интервала (на каждую обработанную совокупность). Каждая выходная таблица состоит из двух столбцов. В первом столбце указывается названия числовых характеристик, во втором– их значения. В заголовке указывается номер совокупности, к которой относится данная таблица (например, Столбец 1).
Свой наибольший размер (18×2) таблица принимает при установке всех четырёх флажков, расположенных в нижней части диалогового окна процедуры. В случае возникновения опасности того, что таблица результатов наложится на уже заполненные ячейки, на экран выводится сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых (для этого надо щёлкнуть на кнопке ОК).
Формирование выборки
Метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой её части на основе положений случайного отбора, называется выборочным методом.
Подлежащая изучению по определённым признакам статистическая совокупность, из которой производится отбор единиц, называется генеральной. Отобранная из генеральной совокупности в случайном порядке некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.
В теории выборочного метода разработаны и в практике статистико-экономических исследований применяются различные способы формирования выборочных совокупностей, обеспечивающие репрезентативность. Организация выборочного наблюдения заключается в определении способа и вида отбора единиц.
Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный.
При повторном способе каждая отобранная в случайном порядке единица после её обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Вероятность попадания любой единицы в выборку равна 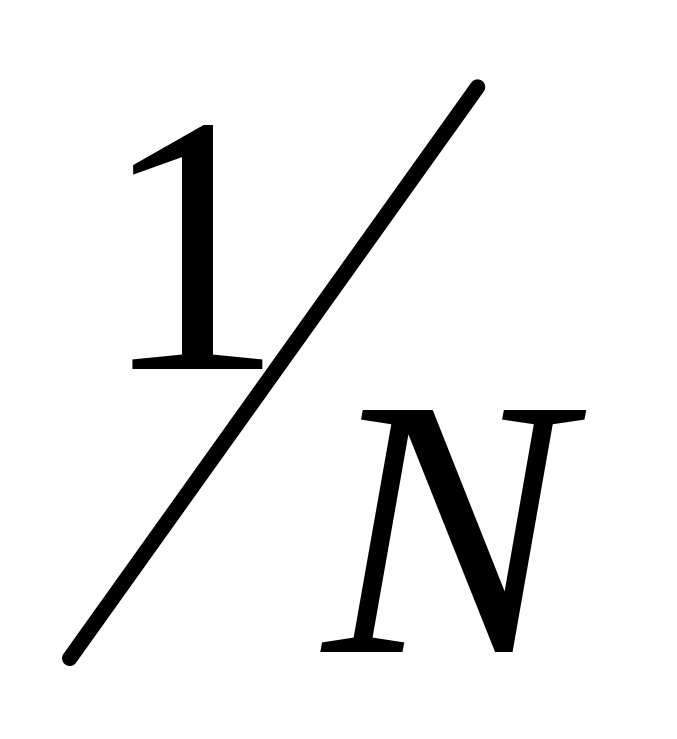
При бесповторном способе отбора попавшая в выборочную совокупность единица после регистрации значений наблюдаемых признаков не возвращается в совокупность, из которой осуществляется дальнейший отбор. Вероятность попадания единицы в выборку изменяется от – для первой отбираемой единицы до 
В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки:
типическая (стратифицированная, расслоенная, районированная);
В Пакете анализа табличного процессора Excel имеется процедура Выборка, реализующая повторную собственно-случайную выборку и механическую выборку с заданным пользователем шагом (периодом) отбора.
Формирование выборки в Excel осуществляется следующим образом:
Единицам генеральной совокупности присваиваются порядковые номера. Для проведения механической выборки генеральная совокупность должна быть каким-либо образом упорядочена, то есть должна быть определённая последовательность в расположении её единиц. Для получения результатов, не содержащих систематическую ошибку выборки, упорядочение необходимо произвести по нейтральному признаку по отношению к изучаемому.
Порядковые номера единиц исходной совокупности вводятся в диапазон ячеек (входной диапазон). Эти номера могут находиться в одном столбце или группе смежных столбцов одинаковой «высоты». При этом число всех ячеек входного диапазона должно равняться числу единиц исходной совокупности. Если среди элементов входного интервала имеются нечисловые данные, то отбор не состоится, а на экране появится сообщение «Выборка– входной интервал содержит нечисловые данные».
В меню Сервис выделяется строка Анализ данных.
В открывшемся диалоговом окне Анализ данных выделяется процедура Выборка и нажимается кнопка ОК. На экране появится диалоговое окно Выборка, которое содержит следующие элементы управления:
поле ввода Входной интервал. В это поле вводится ссылка на диапазон, в котором хранятся номера всех единиц генеральной совокупности, из которой осуществляется выборка.
Метод выборки устанавливается с помощью переключателей Периодический и Случайный. При активизации переключателя Случайный процедура «настраивается» на выполнение случайной выборки с повторением. Нужный объём выборки вводится в поле Число выборок. Единицы генеральной совокупности отбираются случайным образом. Каждая единица исходной совокупности имеет равную со всеми остальными единицами возможность быть включённой в выборку. Любая единица генеральной совокупности может попасть в выборку более одного раза.
При необходимости реализовать механическую выборку активизируется переключатель Периодический. Шаг выборки вводится в поле Период, находящееся справа от переключателя. В выборку войдут элементы исходной совокупности с номерами, кратными заданному периоду. Если входной диапазон состоит из нескольких столбцов, то отбираемые значения будут извлекаться сначала из первого столбца, затем из второго и т.д. Формирование выборки прекращается по достижении конца исходной совокупности.
При формировании случайной выборки выходной интервал представляет собой столбец с числом ячеек, равным заданному объёму выборки. В случае механической выборки число ячеек выходного интервала равно целой части результата деления объёма исходной совокупности на шаг выборки.
Для получения упорядоченной копии номеров единиц совокупности, подлежащих включению в выборку, необходимо щелчком на кнопке Сортировка по возрастанию, расположенной на панели инструментов Стандартная, упорядочить полученный набор номеров.
Корреляционный анализ
В статистике различают две категории зависимостей между признаками:
2) стохастическая, частным случаем которой является корреляционная.
При этом признаки для изучения взаимосвязи по их значению делятся на два класса. Признаки, обуславливающие изменение других, связанных с ними признаков, называются факторными (х). Признаки, изменяющиеся под действием факторных признаков, являются результативными (у).
Функциональной называется связь, при которой каждому значению факторного признака соответствует вполне определённое значение результативного признака. Функциональная связь является строгой, точной, полной зависимостью; проявляется и для каждой единицы совокупности, и во всех случаях наблюдения. Характерной особенностью функциональной связи является то, что в каждом отдельном случае известен полный перечень факторов, влияющих на результативный признак, а также механизм этого влияния, выраженный определённым уравнением.
Стохастическая (вероятностная) связь не проявляется в каждом отдельном случае, а лишь в общем, среднем, при большом числе наблюдений.
Корреляционной называется связь, при которой каждому значению факторного признака может соответствовать несколько значений результативного признака.
Корреляционные связи имеют ряд характеристик:
По форме (аналитическому выражению) корреляционные связи между признаками могут быть линейными (прямолинейными) и нелинейными (криволинейными). При линейной форме равномерное изменение значений одного признака сопровождается более или менее равномерным изменением значений другого признака. Математически она выражается уравнением прямой ух = а + вх, графически — прямой линией. При нелинейной форме равномерному изменению значений одного признака соответствует неравномерное изменение значений другого. Выражается уравнением какой- либо кривой линии: параболы, гиперболы, показательной, степенной, логарифмической, логической функции и др.
По направлению (характеру изменения) корреляционные связи бывают прямыми и обратными. Прямой (положительной) является зависимость, при которой направление изменения значений факторного и результативного признаков совпадает, то есть с увеличением факторного признака, результативный также возрастает, и, наоборот, при уменьшении факторного признака результативный тоже убывает. Обратной (отрицательной) называется связь, при которой изменение значений факторного и результативного признаков осуществляется в разных направлениях, то есть с ростом факторного результативный признак убывает или при убывании факторного признака результативный возрастает.
Степень тесноты корреляционной связи оценивается по специальным шкалам, например, по шкале Чеддока.
Количественный критерий оценки тесноты связи по шкале Чеддока
Величина показателя для измерения тесноты связи
Существуют и другие менее детальные шкалы.
В статистике различают следующие варианты зависимостей:
1) парная корреляция – связь между двумя признаками (результативным и факторным);
2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
3) множественная корреляция – зависимость результативного от двух или более факторных признаков.
В практике статистических исследований выделяют:
корреляционный анализ, который имеет своей задачей количественное измерение тесноты связи между признаками;
регрессионный анализ, который заключается в определении формы связи, построении одно- или многофакторных моделей (уравнений) регрессии;
корреляционно-регрессионный анализ, который включает в себя установление аналитического выражения (формы) и измерение степени тесноты связи.
Следует также различать собственно-корреляционные (параметрические) и непараметрические методы изучения взаимосвязей между признаками. Основу применения собственно-корреляционных методов составляют однородность и необходимость подчинения распределения совокупности по факторным и результативному признаку закону нормального распределения вероятностей. Несоблюдение этих условий обуславливает необходимость применения при изучении взаимосвязей непараметрических методов.
В связи с этим первым этапом изучения зависимостей является установление подчинения распределения результатов наблюдения по изучаемым признакам закону нормального распределения.
На соответствие изучаемого эмпирического распределения нормальному закону указывает близость значений показателей центра распределения – средней арифметической, моды и медианы. С этой целью производится также расчёт и оценка степени существенности показателей асимметрии и эксцесса. В Excel выборочные числовые характеристики вычисляются с помощью процедуры Описательная статистика, входящей в Пакет анализа, и соответствующих встроенных статистических функций (см. раздел 4).
Для проверки гипотезы о законе распределения изучаемого признака используются также специальные статистические критерии. При этом выдвигается гипотеза 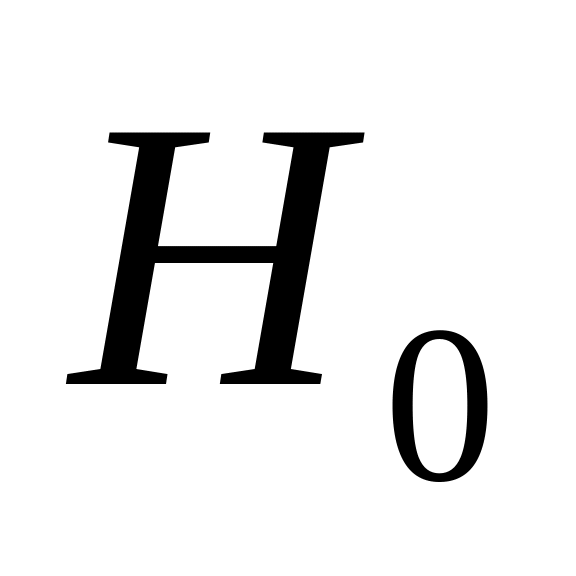
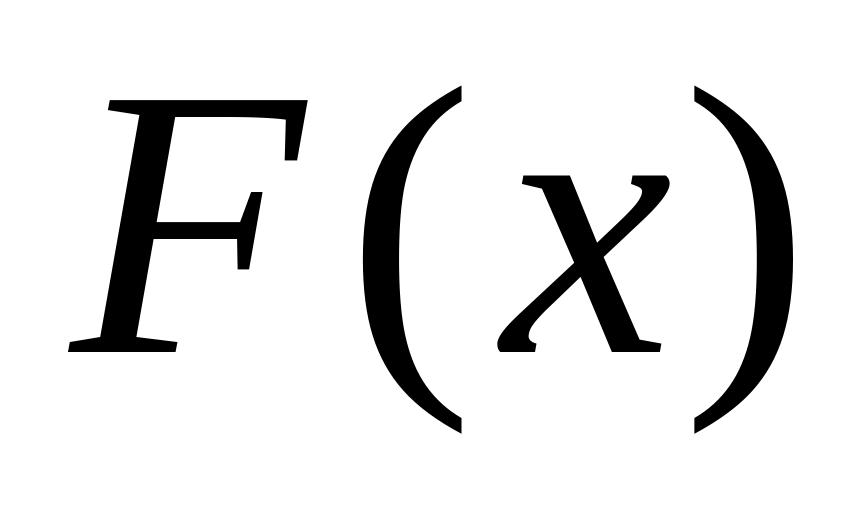

Excel позволяет реализовать проверку статистических гипотез о соответствии эмпирических результатов наблюдения закону нормального распределения на основу вышеуказанных критериев согласия.
Последующий собственно-корреляционный анализ статистических данных, полученных в результате наблюдения, включает в себя:
построение корреляционного поля и корреляционной таблицы;
вычисление выборочных коэффициентов корреляции и корреляционных отношений;
проверка статистических гипотез о значимости корреляционной зависимости.
Корреляционное поле и корреляционная таблица служат для установления наличия и направления зависимости между изучаемыми признаками, дают общее представление об этой зависимости.
В Excel построение поля корреляции (диаграммы рассеивания) между изучаемыми признаками осуществляется при помощи специального средства, служащего для графического изображения статистических данных– Мастера диаграмм (см. 19). Для построения корреляционного поля используется тип Точечная. На палитре Вид выделяется диаграмма в виде изолированных точек, находящаяся в левом верхнем углу палитры.
Расположение точек на графике позволяет в ряде случаев сделать предположение о наличии, направлении и форме взаимосвязи между изучаемыми признаками. Так, линейное расположение точек даёт серьёзное основание для выбора линейной модели, сравнительно небольшой разброс точек относительно воображаемой кривой, проходящей «наилучшим образом» через эти точки, говорит о довольно сильной зависимости между признаками, и наоборот. Расположение точек слева на право свидетельствует о прямой корреляции, а справа налево– об обратной корреляции.
Для подтверждения выводов, сделанных в результате анализа корреляционного поля и в тех случаях, когда корреляция между признаками имеет явно выраженный нелинейный характер и объём выборки велик, данные наблюдения группируют и представляют их в виде корреляционной таблицы, состоящей из 
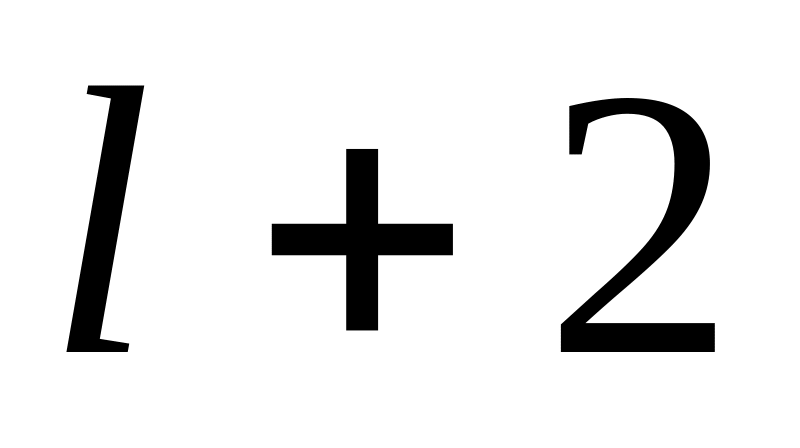

Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. В Excel для группировки данных способом равных интервалов используются процедура Гистограмма, входящая в Пакет анализа (см стр.14).
– середина -го интервала группировки по факторному признаку;
– середина 
– групповая частота «клетки», находящейся на пересечении строки и столбца корреляционной таблицы;
– групповая частота -го интервала группировки по факторному признаку (число наблюдений в -й строке);
–групповая частота -го интервала группировки по результативному признаку (число наблюдений в -м столбце);
–объём изучаемой совокупности (общее число наблюдений).
Заполнение корреляционной таблицы даёт довольно наглядное представление о характере зависимости между изучаемыми признаками.
Для количественного измерения степени тесноты связи служат выборочные коэффициенты корреляции и корреляционные отношения.
Линейный коэффициент корреляции рассчитывается для определения тесноты и направления связи между двумя корреляционными признаками в случае наличия между ними линейной зависимости и распределения значений признаков близкого к нормальному. Линейный коэффициент корреляции может принимать значение от -1 до +1. Чем ближе коэффициент корреляции к 1, тем сильнее (теснее) связь между признаками. Для определения характера связи используют шкалу Чеддока.
В теории разработаны и на практике применяются различные модификации формулы расчёта данного коэффициента:


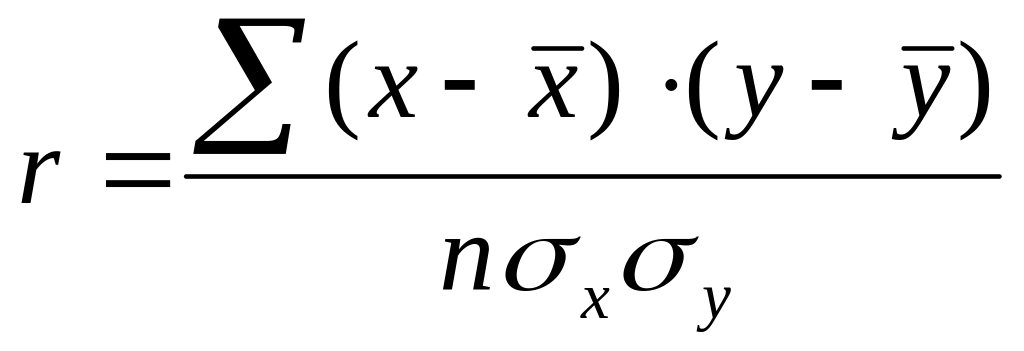


где 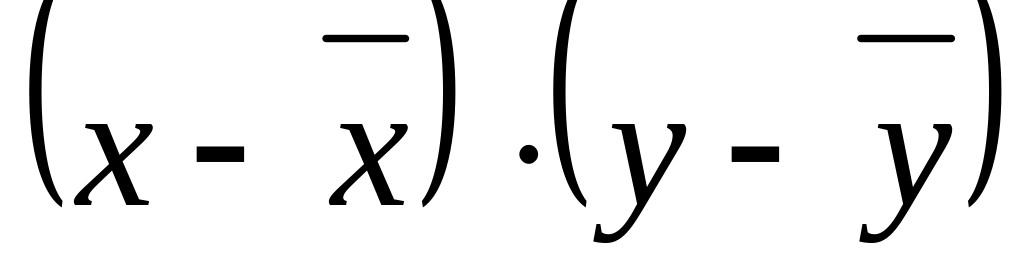


n – число наблюдений.
Квадрат коэффициента корреляции (r 2 ) носит название коэффициента детерминации. Он показывает долю вариации результативного признака, обусловленную влиянием вариации факторного признака.
При наличии нелинейной зависимости используется более универсальный показатель измерения тесноты связи: корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Расчет эмпирического корреляционного отношения осуществляется по сгруппированным данным наблюдения и основан на использовании теоремы (правила) сложения дисперсий:
Эмпирическое корреляционное отношение определяется по формуле:
Межгрупповая дисперсия характеризует ту часть колеблемости результативного признака, которая складывается под влиянием изменения факторного признака, положенного в основание группировки:
Средняя из внутригрупповых дисперсий оценивает ту часть вариации результативного признака, которая обусловлена действием других, прочих, «случайных» причин:


Общая дисперсия характеризует вариацию результативного признака, обусловленную влиянием всех факторов:
Расчёт теоретического корреляционного отношения в Excel осуществляется в рамках регрессионного анализа, поэтому будет рассмотрен в следующем разделе.
В Excel вычисление выборочного коэффициента корреляции осуществляется с помощью процедуры Корреляция, входящей в Пакет анализа, и встроенных статистических функций КОРРЕЛ, ПИРСОН и КВПИРСОН.
При применении процедуры Корреляция в поле Входной интервал диалогового окна этой процедуры вводится ссылка на входной диапазон (на диапазон, содержащий данные наблюдения, подлежащие обработке). Входной диапазон должен содержать 
Назначение переключателя Группирование, флажка Метки и группы переключателей Выходной интервал/Новый рабочий лист/ Новая книга рассмотрено в первом разделе на стр.8-9.
Статистические функции КОРРЕЛ и ПИРСОН вычисляют выборочную оценку линейного коэффициента корреляции по первой формуле, представленной на стр. 34, и дублируют друг друга. Синтаксис функции КОРРЕЛ (массив 1; массив 2), где массив 1– диапазон ячеек, в который введены значения факторного признака (например, А1:А25), а массив 2– диапазон ячеек, в который введены значения результативного признака (например, В1:В25). Статистическая функция КВПИРСОН вычисляет квадрат выборочного коэффициента корреляции.
Для вычисление эмпирического корреляционного отношения в Excel не предусмотрено специальных статистических процедур и встроенных функций. Вычисление корреляционного отношения осуществляется по представленным выше формулам и требует предварительного построения корреляционной таблицы и ряда вспомогательных расчётов.
Значимость линейного коэффициента корреляции проверяется на основе t – критерия Стьюдента. При этом выдвигается и проверяется гипотеза ( 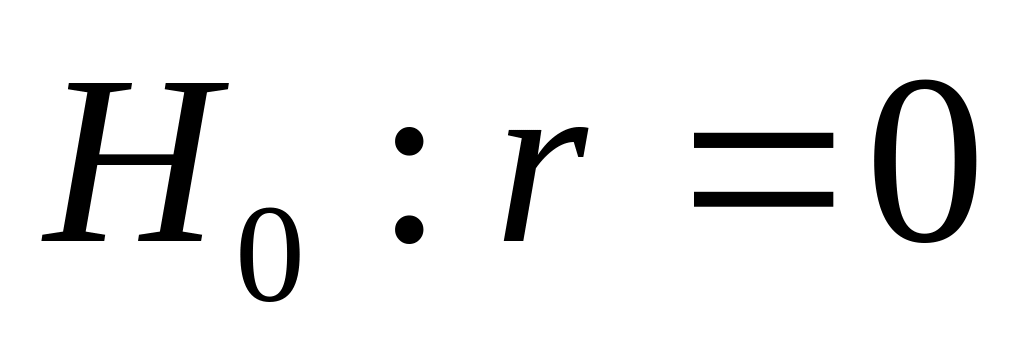

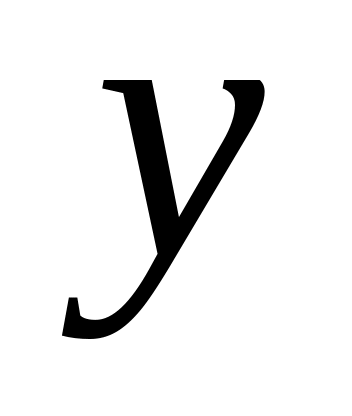
Фактическое значение t — критерия рассчитывается по формуле — для совокупностей n 100):

Вычисленное значение t – критерия сравнивается с критическим его значением при принятом уровне занятости α и числе степеней свободы k = n-2. В социально-экономических исследованиях уровень значимости α обычно принимается равным 0,05.
При «ручной» проверке гипотезы критические значения t находятся по таблице распределения Стьюдента. Если расчётное значение t – критерия больше критического, то гипотеза о том, что линейный коэффициент корреляции в генеральной совокупности равен нулю и лишь в силу случайных обстоятельств оказался равен проверяемому значению, отклоняется, то есть коэффициент корреляции признаётся значимым, а связь между признаками – статистически существенной. Если расчётное значение t – критерия меньше критического, то нулевая гипотеза принимается, что означает, что коэффициент корреляции в генеральной совокупности в действительности равен нулю и соответственно эмпирический коэффициент корреляции существенно не отличается от нуля.
В Excel проверка гипотезы об отсутствии корреляции между изучаемыми признаками осуществляется следующим образом:
В ячейку (например, В1) вводится значение выборочного коэффициента корреляции 
В ячейку В2 для определения расчётного значения t – критерия вводится формула (*): = В1*КОРЕНЬ (115/(1-В1^2)) ( = 117);
В ячейку В3 для нахождения критического значения t – критерия Стьюдента при уровне значимости α= 0,05 и числе степеней свободы k =115 вводится формула: = СТЬЮДРАСПОБР (0.05;115);
Полученные расчётное и критическое значения t – критерия Стьюдента сравниваются, и делается вывод об отклонении или принятии нулевой гипотезы на уровне значимости 
Для оценки значимости корреляционного отношения 
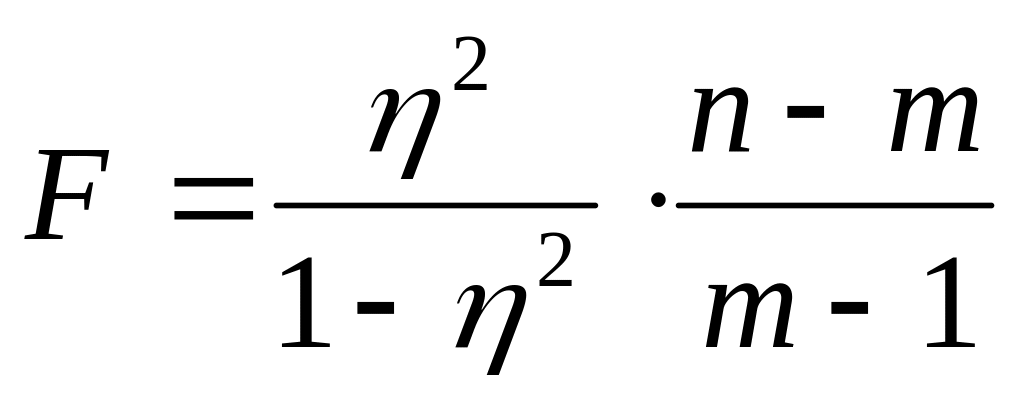
где n — число наблюдений; m – число интервалов группировки или параметров в уравнении регрессии.
При этом проверяется гипотеза 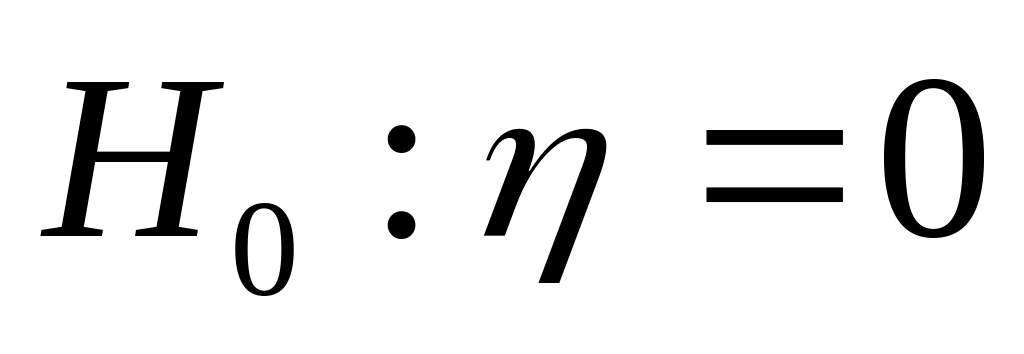

При «ручной» проверке гипотезы используются специальные таблицы F – распределения. В них указывается предельные (критические) значения F – критерия для различных степеней свободы k1 и k2, которые могут быть превзойдены с вероятностью α = 0,05.
В Excel проверка гипотезы об отсутствии корреляции между изучаемыми признаками осуществляется следующим образом:
В ячейку В1 вводится объём совокупности (например, 132) в ячейку В2– число интервалов группировки или параметров в уравнении регрессии (например, 12); в ячейку В3– значение выборочного корреляционного отношения;
В ячейку Е1 для нахождения расчётного значения F – критерий Фишера вводится формула (**): = В3^2*120/(1-В3^2)*11;
В ячейку Е2 для определения критического значения F – критерий Фишера для принятого уровня значимости =0,05 и чисел степеней свободы k1=m-1 (11) и k2=m-n (120) вводится формула: = FРАСПОБР (0.05;11;120).
Полученные расчётное и критическое значения F – критерий Фишера сравниваются, и делается вывод об отклонении или принятии нулевой гипотезы и соответственно о значимости или незначимости корреляционного отношения.
Множественный коэффициент корреляции вычисляется статистической процедурой Регрессия (см. следующий раздел).
Рассмотренные выше вычисления относятся к собственно-корреляционным, параметрическим методам изучения связей.
В случаях, когда анализируется взаимосвязь между количественными признаками, форма распределения которых отличается от нормальной, а также между качественными признаками, используются так называемые непараметрические методы. В основу этих методов положен принцип нумерации значений признаков статистического ряда.
Значения факторного признака записываются в возрастающем или убывающем порядке, а затем ранжируются соответствующие им значения результативного признака. При этом каждой единице в упорядоченном ряду присваивается порядковый номер, который будет её рангом. В случаях наличия одинаковых вариантов каждому из них присваивается среднее арифметическое значение их рангов.
Для определения рангов в Excel предусмотрены статистическая процедура Ранг и персентиль и статистическая функция РАНГ.
Использование процедуры Ранг и персентиль заключается в следующем:
В меню Сервис выделяется строка Анализ данных.
В открывшемся окне Анализ данных выделяется процедура Ранг и персентиль, нажимается кнопка ОК. На экране появляется диалоговое окно Ранг и персентиль.
В поле Входной интервал вводится ссылка на диапазон ячеек, содержащий данные, подлежащие ранжированию. Входной диапазон может быть столбцом или группой смежных столбцов (строкой или группой смежных строк). Если входной диапазон представляет собой группу столбцов (строк), то процедура воспринимает каждый столбец (строку) как отдельную выборку.
Устанавливается переключатель Группирование в нужное положение (по столбцам или строкам).
Флажок Метки устанавливается, если первая строка (столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок не устанавливается.
Щелчком на переключателе Выходной интервал активизируется поле ввода, находящее справа от этого переключателя и вводится в него ссылка на левую верхнюю ячейку таблицы результатов решения. В случае необходимости результаты выводятся на Новый рабочий лист или Новую рабочую книгу. Нажимается кнопка ОК.
Статистическая функция РАНГ имеет следующий синтаксис: РАНГ (число; массив; порядок):
число– номер единицы совокупности, ранг которой надо определить. Если необходимо осуществить ранжирование всей совокупности сразу, то вводится диапазон ячеек, в котором находятся данные, подлежащие обработке;
массив– массив или диапазон ячеек, содержащий единицы исследуемой совокупности (неупорядоченные данные наблюдения);
порядок– величина, определяющая, как упорядочивать (ранжировать) массив:
– если порядок равен 0 или пропущен, массив упорядочивается в порядке убывания;
– если порядок– любое число, не равное нулю, то массив упорядочивается по возрастанию.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют коэффициенты ранговой корреляции Спирмена и Кендалла.
Коэффициент корреляции рангов (Спирмена) определяется по формуле:
r = 
d – разность между рангами соответствующих величин двух признаков;
n – число единиц в ряду (число пар рангов).
Коэффициент корреляции рангов принимает любые значения от -1 до +1. Если все ранги строго изменяются в одном и том же порядке, то d=0, а r=1. Если же ранги изменяются строго в противоположных направлениях, то r= -1. Значение r=0 характеризует отсутствие связи.
В Excel вычисление коэффициента ранговой корреляции Спирмена осуществляется следующим образом:
1. Вводятся заголовки исходных и расчётных данных, необходимых для расчёта коэффициента корреляции рангов: в ячейку А1– названия единиц изучаемой совокупности, в ячейку В1– название факторного признака, в ячейку С1– названия результативного признака, в ячейку D1– символ 

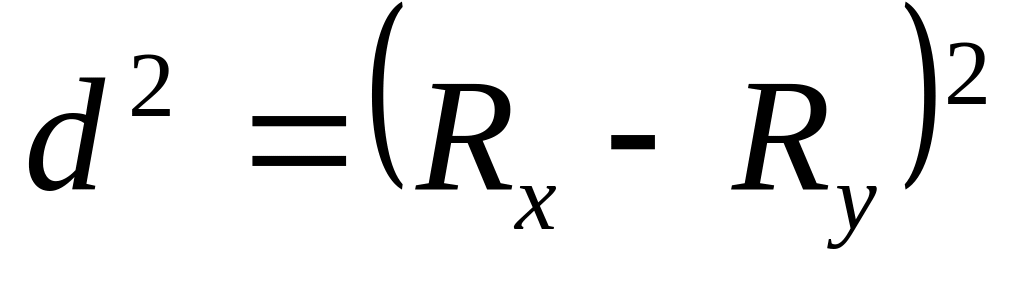
2. Производится ввод исходных данных: в диапазон ячеек столбца А вводятся названия или номера единиц изучаемой совокупности; в диапазон ячеек столбца В (например, В2:В11)– значения факторного признака, в диапазон ячеек столбца С (С2:С11)– значения результативного признака.
3. В диапазонах ячеек D2:D11 и Е2:Е11 определяются соответственно ранги по факторному и результативному признаку с помощью описанной выше процедуры Ранг и персентиль или функции РАНГ, для чего вводятся формулы массива = РАНГ (В2:В11; В2:В11;1) и = РАНГ (С2:С11; С2:С11;1).
4. В диапазоне F2:F11 вычислить квадраты разности рангов с помощью формулы массива: = (D2:D11-E2:E11)^2.
5. В ячейках D12, E12 и F12 с помощью кнопки Автосуммирование определить суммы рангов по факторному и результативному признакам и сумму квадрата разности рангов.
6. По формуле рассчитывается выборочная оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента корреляции рангов для совокупностей небольшого объёма (n£30) проверяется по таблице предельных значений коэффициента корреляции рангов Спирмена при заданном уровне значимости a и определённом объёме совокупности.
Значимость r может быть проверена также на основе t – критерия Стьюдента. Расчётное значение критерия определяется по формуле:
tрасч = r×
Значение коэффициента корреляции считается статистически существенным, если расчётное значение t – критерия Стьюдента превосходит его критическое значение при заданном уровне значимости a и числе степеней свободы k=n-2. Критическое значение t – критерия может быть определено по таблице распределения Стьюдента или в Excel по представленному выше в данном разделе порядку.
Коэффициент корреляции рангов Кендалла рассчитывается по формуле:
t= 
n – число наблюдений;
S – сумма разностей между числом последовательностей и числом инверсий по результативному признаку.
Расчёт данного коэффициента выполняется в следующей последовательности:
ранги факторного признака располагаются в порядке возрастания;
ранги результативного признака располагаются в порядке, соответствующем рангам признака х;
для каждого ранга результативного признака определяется сколько чисел, находящихся справа от него (следующих за ним) имеют величину ранга, превышающую его величину. Суммируя полученные таким образом числа, получаем слагаемое P, которое можно рассматривать как меру соответствия последовательностей рангов по x и y, и которое учитывается со знаком «+»;
для каждого ранга y определяется число, следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «-»;
определяется сумма баллов S=P+Q
Коэффициент Кендалла также изменяется в пределах от -1 до +1. При достаточно большом числе наблюдений между коэффициентами корреляции рангов Спирмена и Кендалла существует следующее соотношение: r» 
Вычисления, связанные с коэффициентом ранговой корреляции 

где 
При таком представлении ранжировки формула коэффициента корреляции рангов Кендалла имеет вид:

где 



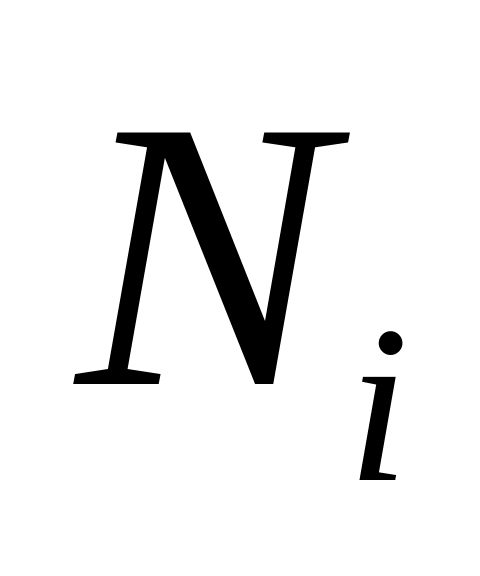
В Excel вычисление коэффициента ранговой корреляции Кендалла осуществляется по формуле (****) следующим образом:
1. Вводятся заголовки исходных и расчётных данных, необходимых для расчёта коэффициента корреляции рангов: в ячейку А1– названия единиц изучаемой совокупности, в ячейку В1– название факторного признака, в ячейку С1– названия результативного признака, в ячейку D1– символ , обозначающий ранг по факторному признаку, в ячейку Е1– символ , обозначающий ранг по результативному признаку, в ячейку– F– символ , обозначающий квадрат разности между рангами соответствующих величин двух признаков.
2. Производится ввод исходных данных: в диапазон ячеек столбца А вводятся названия или номера единиц изучаемой совокупности; в диапазон ячеек столбца В (например, В2:В11)– значения факторного признака, в диапазон ячеек столбца С (С2:С11)– значения результативного признака.
3. В диапазонах ячеек D2:D11 и Е2:Е11 определяются соответственно ранги по факторному и результативному признаку с помощью описанной выше процедуры Ранг и персентиль или функции РАНГ, для чего вводятся формулы массива = РАНГ (В2:В11; В2:В11;1) и = РАНГ (С2:С11; С2:С11;1).
4. Выделяется диапазон D1:E11, в котором находятся ранги по факторному и результативному признакам, нажимается кнопка Копировать на панели инструментов Стандартная.
5. Выделяется ячейка F1. В меню Правка выделяется команда Специальная вставка.
6. В открывшемся диалоговом окне Специальная вставка в группе переключателей Вставить установливается переключатель Значения и нажимается кнопка ОК. В диапазоне F2:G11 появятся «копии» рангов.
7. Выделяется диапазон F1:G11. В меню Данные выделяется команда Сортировка.
8. В открывшемся окне Сортировка диапазона в раскрывшемся списке Сортировать по выбирается поле , по которому надо выполнить сортировку, и установливается переключатель по возрастанию; в группе переключателей Идентифицировать поля по установливатся переключатель подписям (первая строка диапазона) и нажимается кнопка ОК.
В диапазоне F2:G11 появятся ранги по факторному и результативному признакам, отсортированные в порядке возрастания рангов факторного признака.
9. В ячейку Н2 вводится формула массива = СУММ (ЕСЛИ ($G3:$G11>G2;1;0)), нажимаются клавиши Ctrl+Shift+ Enter и затем эта формула копируется в ячейки Н3:Н11. В диапазоне Н2:Н11 появятся числа 
10. Суммируя эти числа в ячейке Н12, находится выборочное значение .
11. Используя формулу = 4* Н12/(10^2-10)-1 (машинный аналог формулы (****)), находится выборочное значение .
Существенность коэффициента корреляции рангов Кендалла проверяется
–при малом объёме совокупности ( 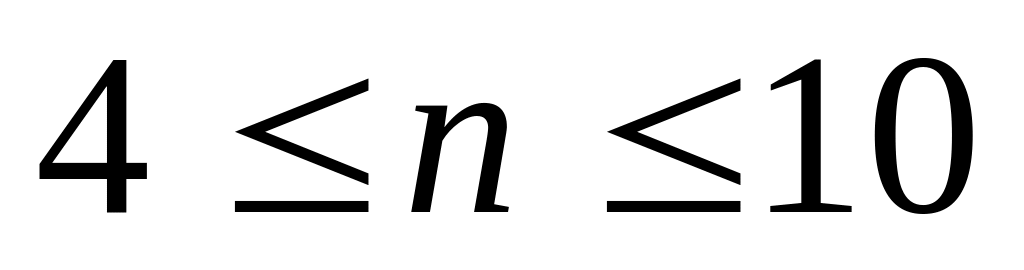
– при больших n для заданного уровня значимости a по формуле:
t>ta× 
ta – коэффициент, определяемый по таблице нормального распределения.
Регрессионный анализ
Регрессионным анализом называется раздел статистики, объединяющий практические методы исследования формы корреляционной зависимости между изучаемыми признаками единиц исследуемой совокупности.
В регрессионном анализе различают парную и множественную регрессию. Парная регрессия описывает связь между двумя признаками: факторным и результативным. Множественная регрессия описывает зависимость результативного признака от нескольких факторных признаков.
Регрессионной моделью системы взаимосвязанных признаков принято считать такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака, обладает высоким (не ниже 0,5) коэффициентом детерминации и коэффициентами регрессии, интерпретируемыми в соответствии с теоретическим знанием о природе связей в изучаемой системе. Приведённое определение включает достаточно строгие условия: не всякое уравнение регрессии можно считать моделью.
Регрессионный анализ включает в себя следующие основные этапы:
выбор модели регрессии;
оценка параметров выбранной модели регрессии;
проверка значимости параметров модели регрессии и их интерпретация;
проверка адекватности построенной модели регрессии.
Выбор аналитической формы связи осуществляется на основе:
логического теоретического анализа;
графического изображения зависимости в виде эмпирической линии регрессии;
опыта предыдущих исследований, где выбранные формы связи давали удовлетворительные результаты;
различных статистико-математических критериев адекватности конкурирующих уравнений регрессии (остаточных дисперсий, ошибок аппроксимации и др.).
Наиболее разработанной в теории статистики является методология парной регрессии. При этом для изучения связи между изучаемыми признаками применяются различного вида уравнения (типы математических функций) линейной и нелинейной зависимостей.
При анализе линейной связи применяется прямолинейная функция, математическим выражением которой является уравнение прямой линии:
При анализе нелинейных связей используются следующие функции:
параболическая yx=a+bx+cx 2
гиперболическая yx=a+
показательная yx=ab x
логистическая yx= 
Решение математических уравнений связи предполагает вычисление по исходным данным их параметров a и b. Это осуществляется способом выравнивания эмпирических (фактических) данных методом наименьших квадратов (МНК). В основу этого метода положено требование минимальности суммы разности квадрата отклонений эмпирических значений результативного признака от его выровненных (теоретических) значений yxi, полученных по выбранному уравнению регрессии:

Параметры b1,… bn в уравнении регрессии называют коэффициентами регрессии. Если связь по направлению прямая – он имеет положительное значение, если обратная – отрицательное. При линейной связи коэффициент регрессии показывает на сколько единиц своего измерения в среднем изменяется величина результативного признака при изменении факторного признака на единицу своего измерения.
В Excel имеется две процедуры и восемь встроенных функций для регрессионного анализа. Они вычисляют не только выборочные параметры регрессии, но и ещё ряд дополнительных выборочных характеристик исследуемой регрессионной зависимости. К числу таких характеристик относятся:
общая сумма квадратов 


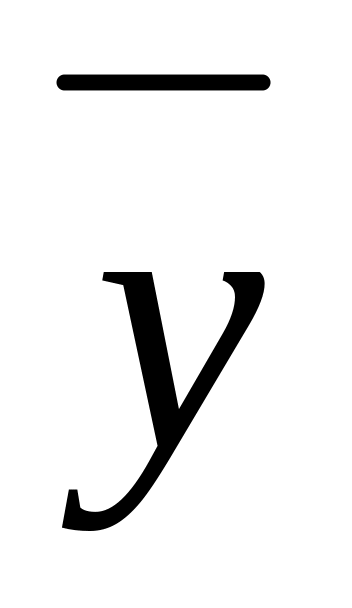
сумма квадратов, обусловленная регрессией 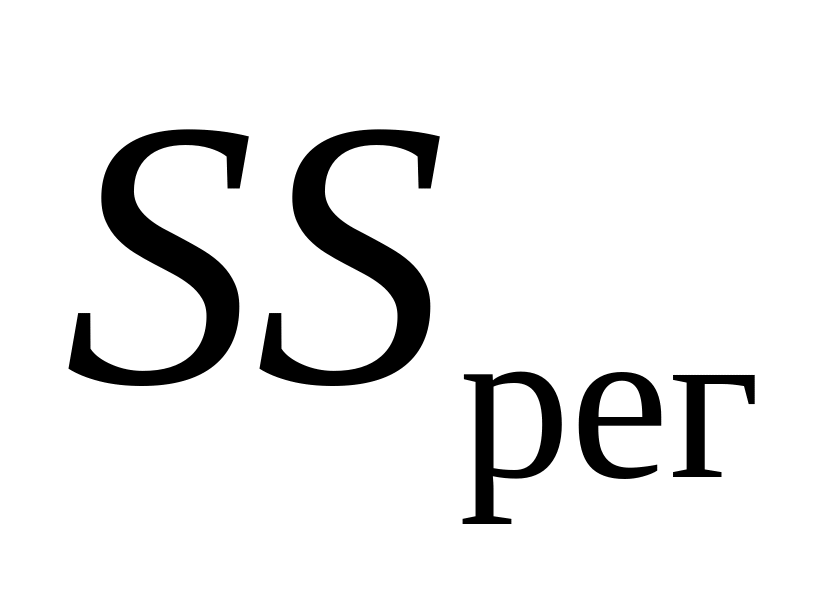

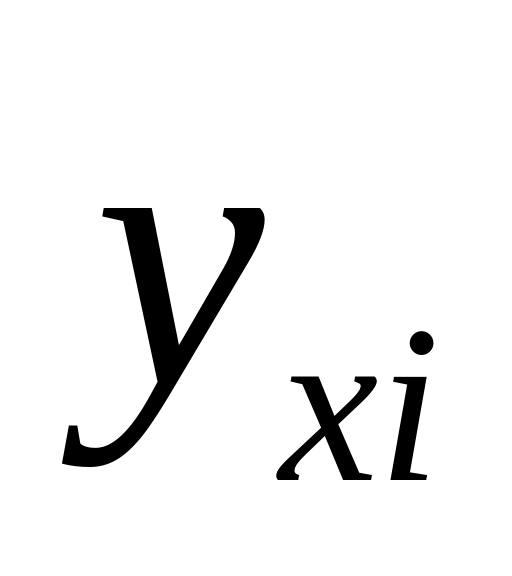
сумма квадратов остатков 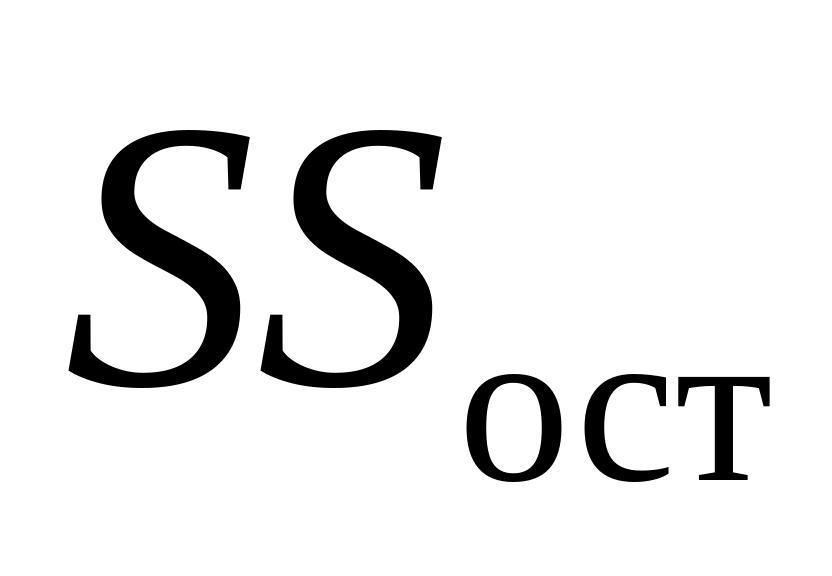

числа степеней свободы этих сумм 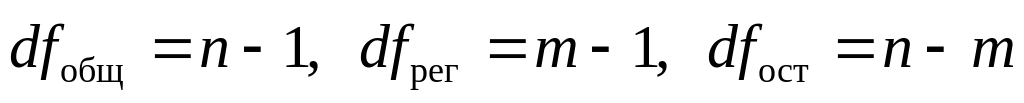
средний квадрат регрессии или факторная (систематическая) дисперсия– 
средний квадрат остатков или остаточная (случайная) дисперсия– 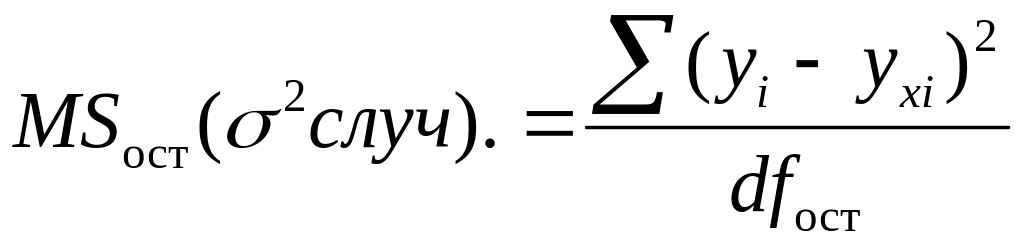
Эти дисперсии связаны между собой равенством, носящим название «правило сложения дисперсий»– 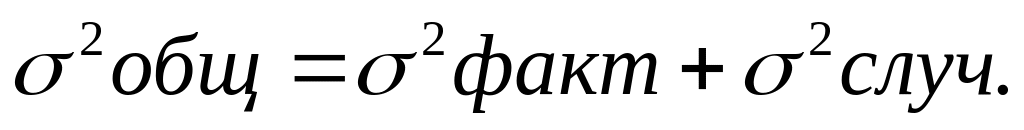

множественный коэффициент (индекс) корреляции 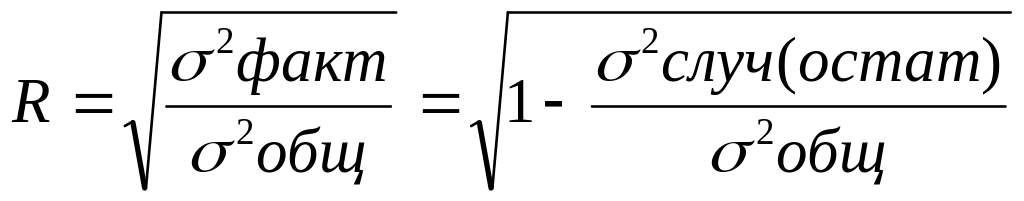
коэффициент детерминации– 
нормированный (скорректированный) коэффициент детерминации – 
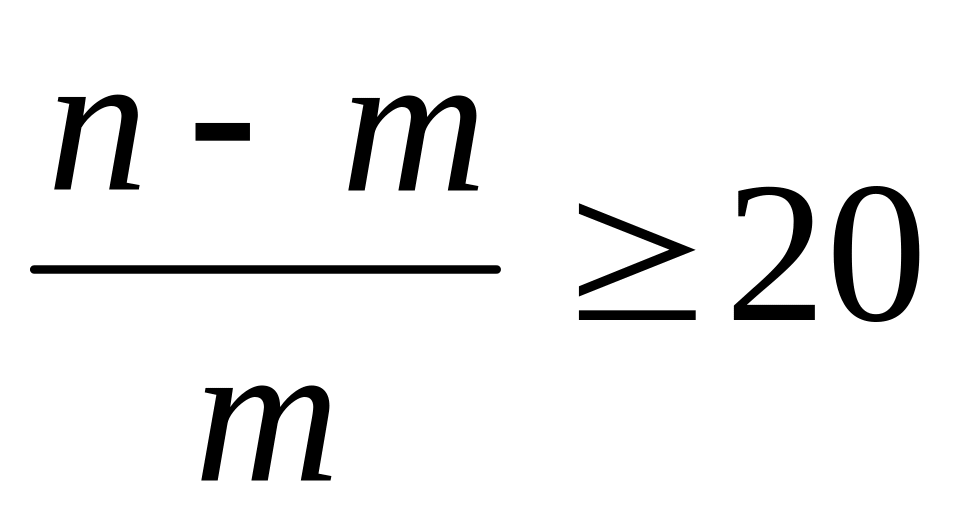
стандартная ошибка аппроксимации (средняя квадратическая ошибка) уравнения регрессии:
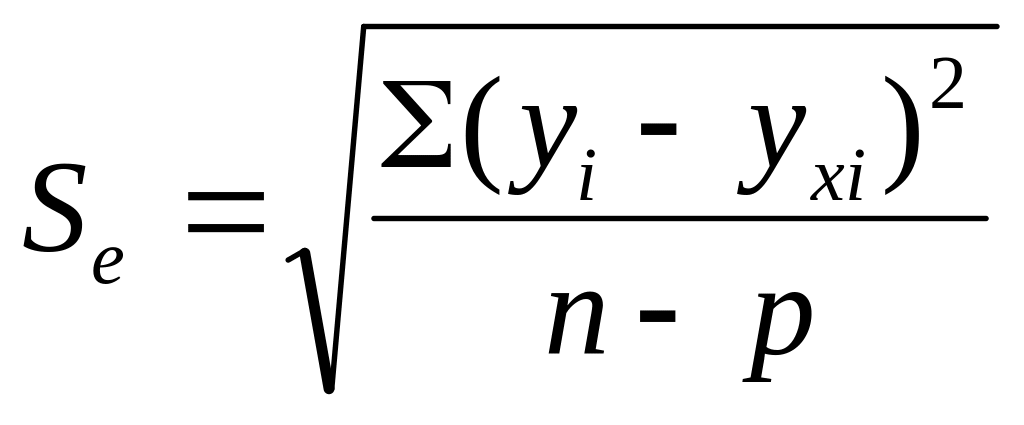
где 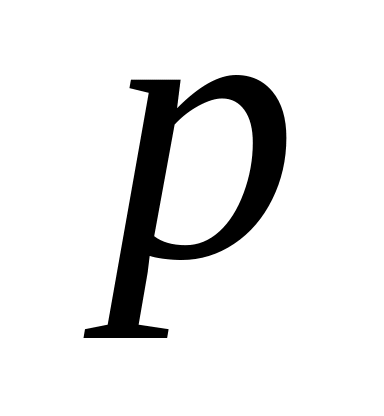
стандартное отклонение параметров регрессии– 

где 

Выборочный коэффициент детерминации и выборочные параметры регрессии, вычисленные по ограниченному числу единиц изучаемой совокупности, всегда содержат элемент случайности, в связи, с чем возникает необходимость проверки значимости этих выборочных характеристик.
При проверке значимости параметра регрессии 

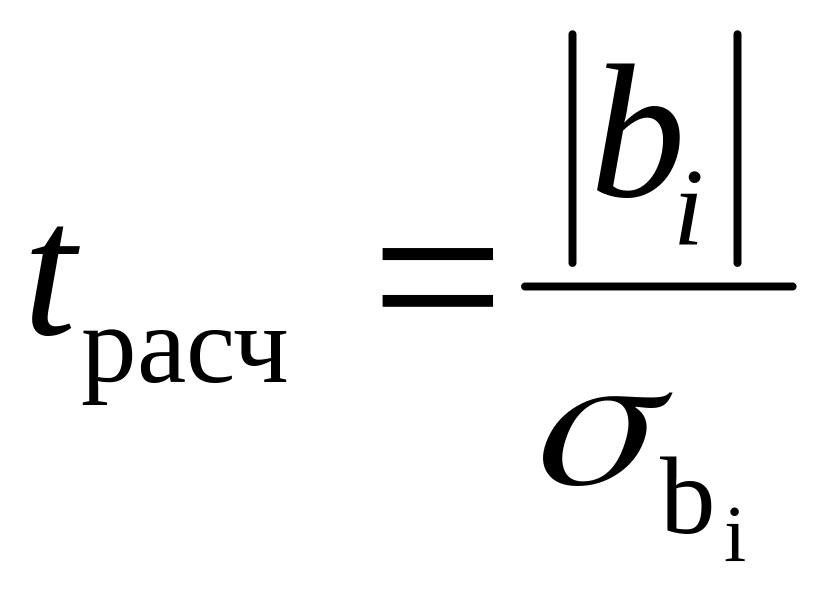
Параметр признаётся статистически значимым, если расчётное значение t – критерия Стьюдента превосходит его критическое значение, определяемое при заданном уровне значимости α и числе степеней свободы 
При проверке значимости коэффициента детерминации выдвигается гипотеза 
Расчётное значение критерия Фишера–Снедекора, вычисляется по формуле:
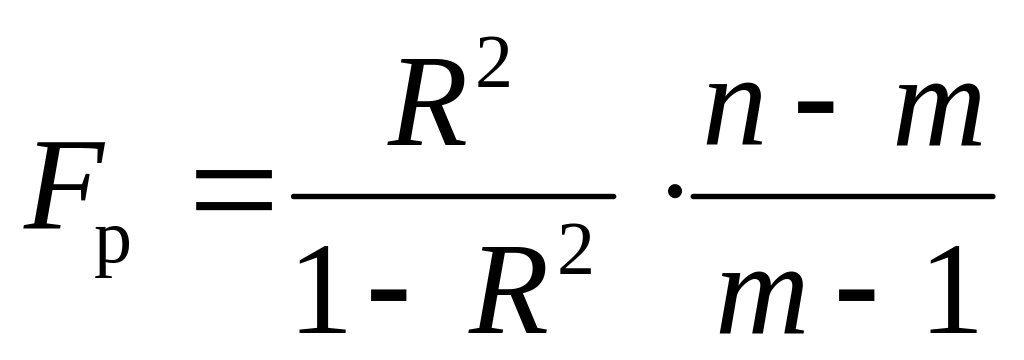
Если 



В качестве меры адекватности модели регрессии используется также процентное отношение стандартной ошибки 


Если 
В Excel для проведения регрессионного анализа существует статистическая процедура Регрессия, позволяющая осуществлять парную линейную, параболическую (полиноминальную) и множественную регрессии. Для выбора формы связи целесообразно построить корреляционное поле, воспользовавшись специальным средством Мастер диаграмм, выбрав тип Точечная (см. предыдущий раздел).
Парная линейная регрессия в Excel осуществляется следующим образом:
Осуществляется ввод исходных данных, т.е. значений факторного и результативного признака.
В меню Сервис выделяется строка Анализ Данных.
В открывшемся окне Анализ данных выделяется процедура Регрессия и нажимается кнопка ОК. Откроется диалоговое окно Регрессия с пульсирующим курсором в поле ввода Входной интервал Y.
С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения результативного признака Y. В поле ввода Входной интервал Y появится соответствующая ссылка.
Нажатием клавиши Tab осуществляется переход в поле ввода Входной интервал Х. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения факторного признака Х. В поле ввода Входной интервал Х появится соответствующая ссылка.
Устанавливается флажок в группе флажков Остатки. В данную группу входят следующие флажки:
– флажок Остатки. При его установке на экран выводится таблица ВЫВОД ОСТАТКОВ, в состав которой входит столбец Остатки;
– флажок График остатков. При активизации этого флажка на экран выводятся графики зависимости остатков от регрессионных переменных (по одному графику на каждую переменную);
– флажок Стандартизированные остатки. При установке данного флажка в таблицу ВЫВОД ОСТАТКОВ добавляется столбец центрированных нормированных (стандартизированных), которые получаются из остатков 
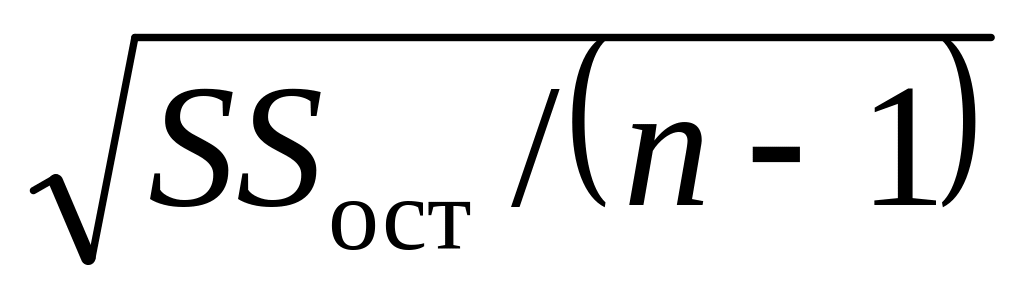
– флажок График подбора. При установке этого флажка на рабочий лист выводятся точечных графиков (по числу контролируемых переменных). На графике, связанном с -й контролируемой переменной 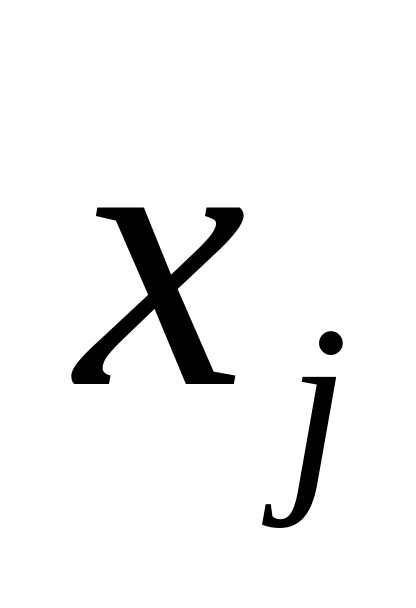

– флажок График нормальной вероятности. При активизации этого флажка на экран выводятся таблица ВЫВОД ВЕРОЯТНОСТИ и график функции, обратной эмпирической функции распределения результативного признака, выполненный на «вероятностной нормальной бумаге».
Щелчком на кнопке ОК запускается процедура Регрессия.
Помимо этого процедура содержит также следующие элементы управления:
Флажок Константа-ноль. Устанавливается в том случае, когда необходимо, чтобы линия регрессии проходила через начало координат. При этом параметр равен нулю и число параметров регрессии равно числу факторов.
флажок Уровень надёжности. Устанавливается в том случае, когда помимо доверительных интервалов для параметров регрессии, соответствующих используемой по умолчанию «стандартной» доверительной вероятности 95%, необходимо вычислить доверительные интервалы, доверительная вероятность которых отличается от «стандартной». «Нестандартная» вероятность, выраженная в процентах, вводится в поле, расположенное справа от рассматриваемого флажка. Если этот флажок не установлен, то выходной таблице параметров регрессии будут одинаковые пары столбцов, содержащие доверительные границы для параметров регрессии, соответствующие одной и той же доверительной вероятности 95% (при редактировании таблицы их можно убрать).
Назначение флажка Метки и переключателей Выходной интервал/Новый рабочий лист/ Новая книга рассмотрено в 1 разделе.
После запуска процедуры Регрессия на рабочем листе появляются три таблицы результатов этой процедуры. В первой таблице «Регрессионная статистика» содержатся значения множественного коэффициента корреляции, коэффициента детерминации, нормированного коэффициента детерминации, стандартная ошибка уравнения регрессии и число наблюдений. Во второй таблице «Дисперсионный анализ» содержатся значения сумм квадратов и среднего квадрата регрессии, остатков и общие., а также расчётное значение критерия Фишера–Снедекора. В третьей таблице в графе «Коэффициенты» по строке «Y- пересечение» находится значение свободного члена уравнения регрессии , а по строке Х – значение параметра 
Полиноминальная (параболическая) регрессия в Excel осуществляется следующим образом:
1. В ячейки А1, В1 и С1 вводятся метки Y, X и X 2 .
2. В диапазон А2 и далее (например, А2: А15) вводятся значения результативного признака, в диапазон В2 и далее (соответственно В2:В15)– значения факторного признака.
3.В диапазон С2 и далее (С2: С15) вводится формула массива = В2:В15^2 и нажимается комбинация клавиш Ctrl+Shift+ Enter. В диапазоне С2:С15 появится столбец квадратов значений факторного признака.
4. В открывшемся окне Анализ данных выделяется процедура Регрессия и нажимается кнопка ОК. Откроется диалоговое окно Регрессия с пульсирующим курсором в поле ввода Входной интервал Y.
5. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения результативного признака Y. В поле ввода Входной интервал Y появится соответствующая ссылка.
6. Осуществляется переход в поле ввода Входной интервал Х. С помощью мыши выделяется диапазон ячеек, в котором находятся эмпирические значения факторного признака. В поле ввода Входной интервал Х появится соответствующая ссылка.
7. Устанавливается флажок в группе флажков Остатки.
8. Щелчком на кнопке ОК запускается процедура Регрессия.
После запуска процедуры Регрессия на рабочем листе появляются три таблицы результатов этой процедуры.
Множественная линейная регрессия в Excel осуществляется аналогичным образом. При этом в качестве исходных данных вводятся значения результативного и нескольких ( 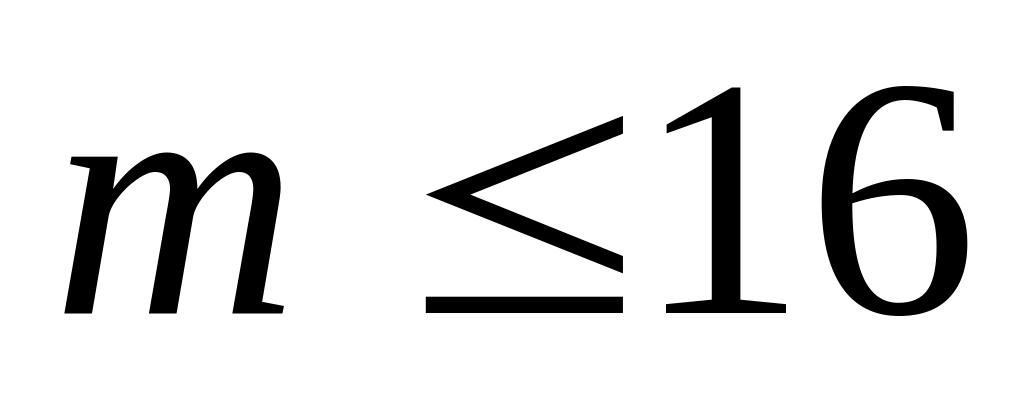
К статистическим функциям, предназначенным для регрессионного анализа в Excel, относятся ЛИНЕЙН, НАКЛОН, ОТРЕЗОК, ТЕНДЕНЦИЯ, ПРЕДСКАЗ, СТОШYХ, ЛГРФПРИБЛ, РОСТ.
Из этих функций интерес представляют функции ЛГРФПРИБЛ, ТЕНДЕНЦИЯ и РОСТ, так как другие функции вычисляют некоторые характеристики, определяемые статистической процедурой РЕГРЕССИЯ, а также дублируют друг друга. Эти же три функции производят вычисления, не предусмотренные статистической процедурой РЕГРЕССИЯ.
Функция ЛГРФПРИБЛ вычисляет выборочные оценки параметров показательной (экспоненциальной) регрессии.
Синтаксис данной функции: ЛГРФПРИБЛ (известные значения у; известные значения х;, конст; стат):
известные значения у– множество значений результативного признака. Данный массив представляет собой вектор-столбец размером 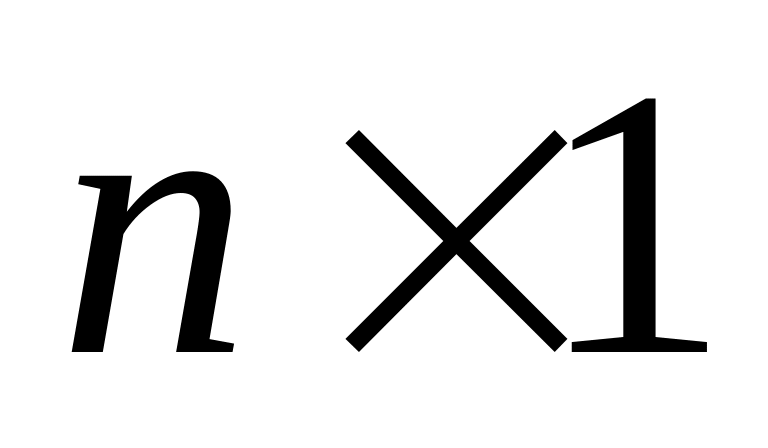
известные значения х–множество значений факторных признаков.
– Если в случае парной регрессии этот аргумент опущен, то при вычислениях в качестве массива известные значения х используется массив натуральных чисел 1,2…и т.д. такого же размера, как и массив известные значения у;
– В случае множественной регрессии, если массив известные значения у представляет собой вектор-столбец, то массив известные значения х должен иметь строк и столбцов. При этом каждый столбец этого массива содержит значений определённого факторного признака;
– При вводе массива чисел известные значения х с клавиатуры для разделения значений в одной строке используют точку с запятой, а для разделения строк– двоеточие.
конст–логическая переменная, определяющая, следует ли включать в уравнение регрессии свободный член.
– Если конст=1 (ИСТИНА) или опущен, то вычисляются и коэффициенты регрессии, и свободный член.
– Если конст= 0 (ЛОЖЬ), то предполагается, что свободный член равен единице.
стат– логическая переменная, определяющая объём выходной информации.
– Если аргумент стат =0 (ЛОЖЬ) или опущен, то функция выдаёт только параметры уравнения регрессии. При этом для вывода результатов решения надо заранее выделить диапазон ячеек размером 
– Если аргумент стат =1 (ИСТИНА), то помимо функция выдаёт дополнительную информацию об исследуемой регрессионной зависимости. В этом случае для вывода результатов решения надо выделить диапазон ячеек размером 
Так как результатом реализации функции является массив чисел, содержащий выборочные характеристики исследуемой регрессионной зависимости, то функция вводится как формула массива Ctrl+Shift+ Enter. Например, = ЛГРФПРИБЛ (А1:А6;В1:В6;1;1).
Функции ТЕНДЕНЦИЯ и РОСТ используются для вычисления расчётных значений результативного признака, соответствующих заданным пользователем значениям факторных признаков, хранящимся в массиве новые значения х. При этом функция ТЕНДЕНЦИЯ вычисляет параметры линейной и других видов регрессии, линейных относительно входящих в них коэффициентов, таких, например, как полиноминальная (параболическая) регрессия 
Функции вводится как формула массива Ctrl+Shift+ Enter.
Синтаксис данных функций идентичен: ТЕНДЕНЦИЯ (известные значения у; известные значения х;, новые значения х,; конст) и РОСТ (известные значения у; известные значения х;, новые значения х,; конст):
известные значения у– множество значений результативного признака. Данный массив представляет собой вектор-столбец размером ;
известные значения х–множество значений факторных признаков.
– Если в случае парной регрессии этот аргумент опущен, то при вычислениях в качестве массива известные значения х используется массив натуральных чисел 1,2…и т.д. такого же размера, как и массив известные значения у;
– В случае множественной регрессии, если массив известные значения у представляет собой вектор-столбец, то массив известные значения х должен иметь строк и столбцов. При этом каждый столбец этого массива содержит значений определённого факторного признака;
– При вводе массива чисел известные значения х с клавиатуры для разделения значений в одной строке используют точку с запятой, а для разделения строк– двоеточие.
новые значения х– новые значения факторных признаков, для которых функция должна вычислить расчётные значения результативного признака;
– В случае множественной регрессии, если массив известные значения у представляет собой вектор-столбец, то массив новые значения х должен иметь столбцов и столько строк, сколько расчётных значений у надо вычислить.
–Массив новые значения х, так же как и массив известные значения х, должен содержать столбец для каждого факторного признака. Число столбцов этих массивов должно быть одинаково.
– Если аргумент новые значения х опущен, то предполагается, что он совпадает с аргументом известные значения х.
конст–логическая переменная, определяющая, следует ли включать в уравнение регрессии свободный член.
– Если конст=1 (ИСТИНА) или опущен, то вычисляются и коэффициенты регрессии, и свободный член.
– Если конст= 0 (ЛОЖЬ), то предполагается, что свободный член равен нулю (в случае линейной регрессии) и единице (в случае экспоненциальной регрессии).
Ряды динамики
Ряд динамики– это ряд числовых значений статистических показателей, расположенных в хронологической последовательности и характеризующих изменение явления во времени.
Ряд динамики состоит из двух элементов:
уровней динамического ряда– числовых значений статистических показателей, характеризующих величину изучаемого явления– 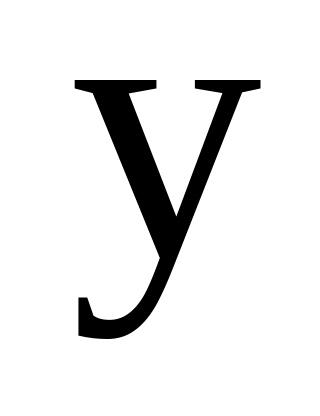
периодов (или моментов) времени, к которым относятся данные уровни – 
Одной из основных задач в процессе анализа уровней динамического ряда является определение основной закономерности (тенденции) их изменений во времени.
При этом выделяются следующие основные компоненты динамического ряда:
основная тенденция (тренд) (Т);
Первые три компоненты формируют систематическую составляющую динамического ряда.
Тренд характеризует устойчивое систематическое изменение динамического ряда, происходящее в течение длительного времени и обусловленное влиянием медленно развивающихся долговременных факторов.
Сезонная компонента– это колебания, периодически повторяющиеся в некоторое определённое время каждого года, дня месяца или часа дня.
Циклическая (периодическая) компонента проявляется в том, что значение изучаемого показателя в течение какого-то времени возрастает, достигает определённого максимума, затем понижается, достигает определённого минимума, вновь возрастает до прежнего значения и т.д.
Четвёртую компоненту формируют случайные колебания, которые являются результатом действия большого количества относительно слабых второстепенных факторов.
Для выявления и характеристики основной закономерности развития явления необходимо выявить первую компоненту динамического ряда – тренд, и погасить влияние других типов колебаний на изменение уровней ряда.
С этой целью проводят выравнивание динамических рядов. Различают два вида выравнивания: механическое (или сглаживание) и аналитическое.
К приёмам механического выравнивания относятся:
усреднение левой и правой половины ряда;
скользящая средняя: простая, взвешенная;
Выбор приема выравнивания зависит от исходной информации и задач исследования.
В среде Excel для выравнивания динамических рядов используются процедуры Скользящее среднее и Экспоненциальное сглаживание, входящие в Пакет анализа.
Сущность метода скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, затем, начиная с третьего и т.д. Таким образом, при расчётах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Этим объясняется название – скользящая средняя.
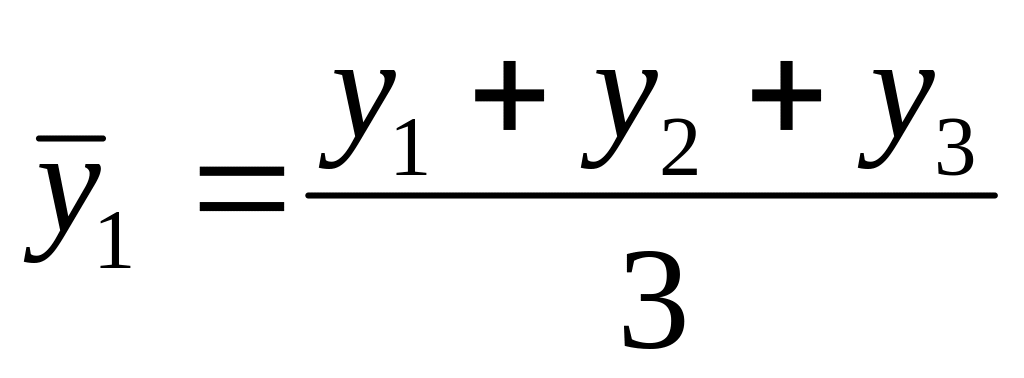


Следует отметить, что при использовании метода скользящей средней «теряются» 
=3 ( 
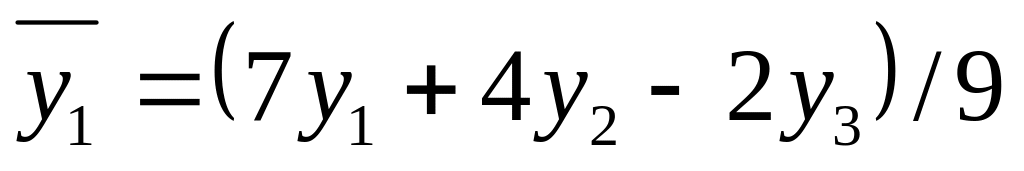

=5( 




Для получения количественной модели, выражающей основную тенденцию изменения уровней динамического ряда во времени, используется приём аналитического выравнивания. Сущность его состоит в том, что основная тенденция развития 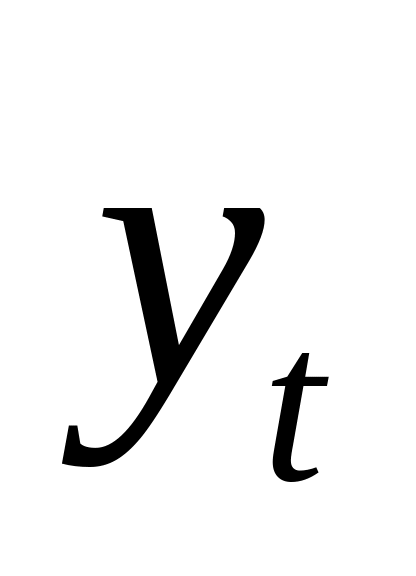
Аналитическое выравнивание производится в следующей последовательности:
1) выделяется этап развития явления и устанавливается характер динамики на этом этапе. Этап развития явления– это период, в течение которого формирование уровней динамического уровня осуществляется под воздействием определённого набора постоянных, периодических и разовых факторов. Решение этой задачи осуществляется не только с помощью статистических методов, а в основном – на базе анализа сущности, природы явлений и общих законов его развития.
2) на основе предположений о той или иной закономерности развития выбирается форма аналитического выражения тренда, то есть вид аппроксимирующей математической функции.
Основанием для выбора уравнения тренда могут служить:
качественный анализ сущности развития данного явления;
результаты предыдущих исследований в данной области;
графическое изображение эмпирических или скользящих уровней ряда динамики;
статистико-математических критериев адекватности.
При анализе рядов динамики используются следующие математические модели:
где 

– начальный уровень тренда в момент или период, принятый за начало отсчёта времени;
– среднее абсолютное изменение за единицу времени;
Параметр определяет направление развития: если 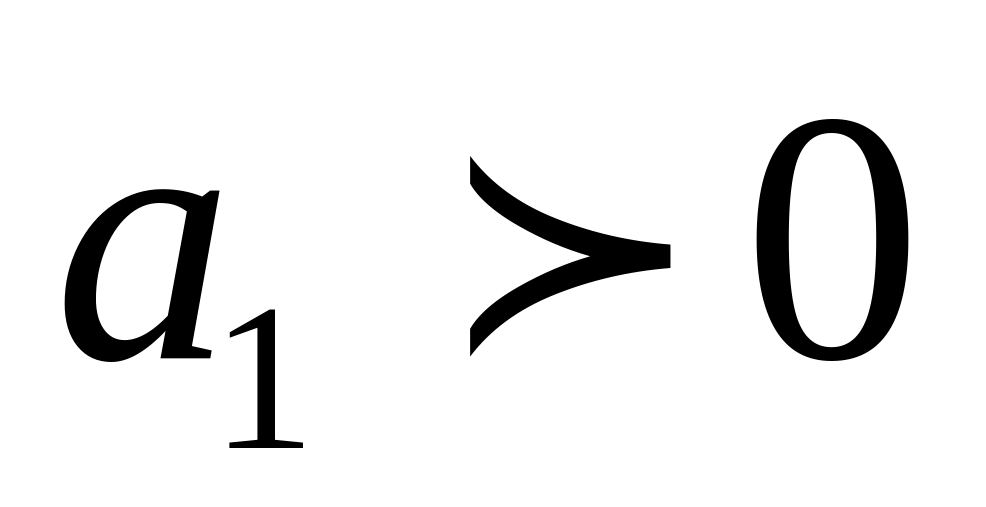

полиноминальная(параболическая) 
Значение параметров и идентично предыдущему уравнению.
Параметр 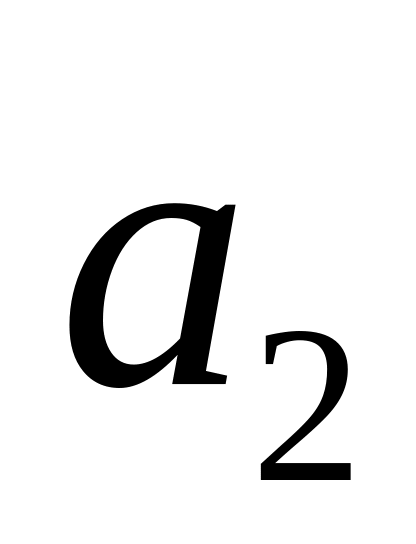
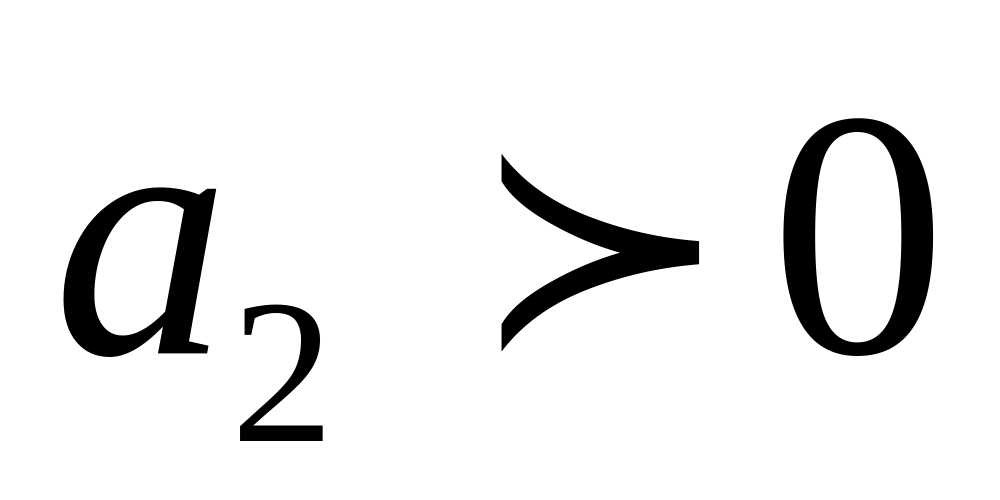
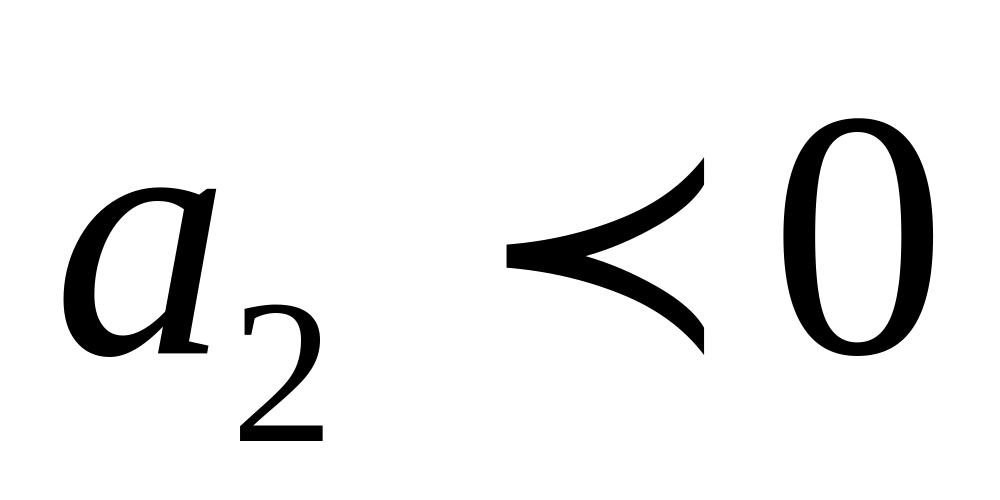
Соответственно при параболической форме тренда возможны следующие варианты развития:
если ; – ускорение роста;
если ; – замедление роста;
если ; – замедление снижения;
если ; – ускорение снижения.
экспоненциальная 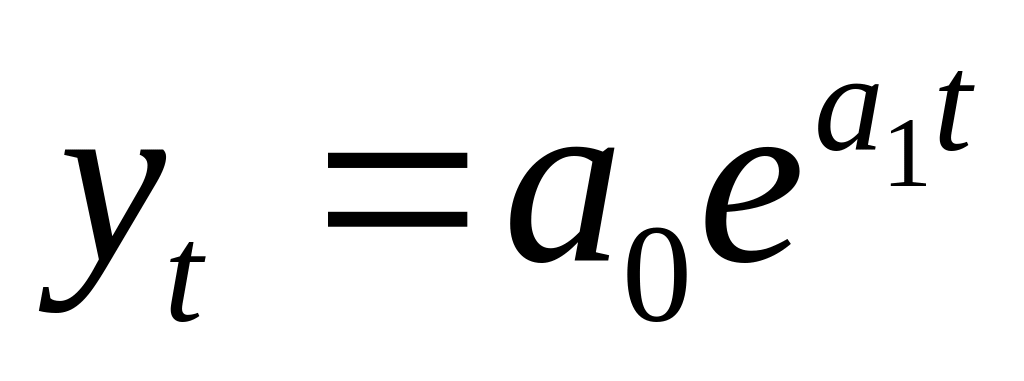
где – константа ряда, –темп изменения в разах. При >1 экспоненциальный тренд выражает тенденцию ускоренного и всё более ускоряющегося возрастания уровней, при 2 = min.
4) На основе синтезированной модели тренда вычисляются теоретические уровни.
Выявление и характеристика основной тенденции развития дают основание для прогнозирования, то есть для определения возможного варианта размеров явления в будущем. Важное значение при прогнозировании имеют вопросы о базе и сроках прогнозирования.
База прогнозирования – длина или продолжительность базисного периода, закономерность которого будет распространяться на будущее.
Срок прогнозирования (период упреждения) – длина будущего периода, на который распространяется закономерность развития явления.
Однозначного ответа на вопрос об определении допустимого срока прогноза нет. В основном придерживаются следующего правила: срок прогноза не должен превышать третьей части длины базы прогноза. Однако в каждом конкретном случае необходимо учитывать особенности изучаемого явления. При этом необходимо, чтобы продолжительность базисного ряда составляла определенный этап в развитии анализируемого явления в конкретных исторических условий.
Установление сроков прогнозирования зависит от цели исследования. Однако следует иметь в виду, особенности характера изучаемого явления. Например, ограниченные физиологические особенности животных (или растений), делают невозможным увеличение продуктивности животных (или урожайности) до бесконечности. Кроме того, необходимо учитывать неустойчивость экономики в условиях переходного периода. Поэтому чем короче сроки прогнозирования периода, тем надежнее результат прогноза.
Разработка прогнозного уровня динамического ряда может осуществляться на основе использования различных методов, наиболее распространённым из которых является метод экстраполяции.
Метод экстраполяции основывается на предположении о неизменности основных факторов, определяющих тенденцию данного показателя, и заключается в распространении закономерностей развития этого показателя, имевших место в прошлом, на будущее.
Более точным и распространённым методом экстраполяции является применение аналитического выражения тренда, при котором в адекватную трендовую модель подставляются значения в будущие годы. Прогнозирование на основе экстраполяции дает возможность получить точечные значения прогнозируемого уровня исследуемого показателя.
Интерполяция– это приближённый расчёт уровней, находящихся внутри ряда динамики, но почему-либо неизвестных. При интерполяции предполагается, что характер тенденции не претерпел существенных изменений в том промежутке времени, уровень которого нам не известен.
Как и экстраполяция, интерполяция может производится на основе на основе выравнивания динамического ряда по какой-либо аналитической формуле.
В Excel сглаживание динамического ряда методом скользящей средней осуществляется следующим образом:
1. В диапазон ячеек вводятся уровни ряда динамики (числовые значения изучаемого статистического показателя).
2.В меню Сервис выделяется строка Анализ данных.
3. В открывшемся окне Анализ данных выделяется процедура Скользящее среднее и нажимается кнопка ОК. На экране появится диалоговое окно Скользящее среднее.
4. В поле ввода Входной интервал этого окна вводится ссылка на диапазон ячеек, содержащий уровни исследуемого ряда динамики. Входной интервал должен состоять из одного столбца, «высота» которого равна числу уровней данного ряда динамики.
5. В поле Интервал вводится размер окна сглаживания (по умолчанию =3).
6. В поле Выходной интервал вводится ссылка на верхнюю ячейку столбца результатов сглаживания. Выходной интервал всегда располагается на том же самом рабочем листе, на котором находится входной интервал, поэтому в диалоговом окне процедуры нет таких позиций, как Новый рабочий лист и Новая рабочая книга. Выходной интервал состоит по крайней мере из одного столбца, содержащего уровни сглаженного ряда. Высота этого столбца равна высоте входного интервала. При установке флажка Стандартные погрешности в выходном интервале появляется ещё один столбец– столбец стандартных погрешностей. В точках, для которых нельзя вычислить сглаженные значения и стандартные погрешности, процедура выводит сообщение # Н/Д! (Нет данных).
7. Устанавливается флажок Вывод графика. Флажок Стандартные погрешности устанавливается при необходимости получения стандартных погрешностей сглаживания. Назначение флажка Метки рассмотрено в 1 разделе.
8. Нажимается кнопка ОК.
Следует иметь в виду, что процедур Скользящее среднее выдаёт сглаженный ряд так называемых адаптивных скользящих средних. Этот ряд сдвинут на шагов вправо относительно «канонического» ряда скользящих средних. Для сравнения простого и адаптивного скользящих средних в диапазоне ячеек, число которых на -1 меньше числа уровней исходного ряда динамики, свободного столбца, рассчитываются значения скользящих средних, вычисленные по канонической формуле = СРЗНАЧ по диапазону из первых уровней динамического ряда (например, при =3 А1:А3). Данная формула вводится в следующую после 
При проведении экспоненциального сглаживания использование одноимённой процедуры аналогично выше рассмотренному порядку. Вместо поля Интервал диалогового окна Скользящее среднее в процедуре Экспоненциальное сглаживание заполняется поле Фактор затухания. В это поле вводится фактор затухания 


При аналитическом выравнивании в Excel используются статистическая процедура Регрессия и статистические функции регрессионного анализа ЛИНЕЙН, ПРЕДСКАЗ, ЛГРФПРИБЛ, ТЕНДЕНЦИЯ и РОСТ, рассмотренные в предыдущем разделе. В этом случае при использовании статистической процедуры Регрессия вместо значений факторного признака вводятся натуральные числа 1,2,…. , обозначающие порядковые номера периодов или моментов времени. При использовании статистических функций натуральные числа можно не вводить, а оставить пропущеным аргумент известные значения х. Тогда при вычислениях в качестве массива известные значения х используется массив натуральных чисел 1,2…и т.д. такого же размера, как и массив известные значения у.
Эффективным средством аналитического выравнивания является процедура Добавить линию тренда, входящая в комплекс графических средств табличного процессора Excel. Она вычисляет параметры выбранной пользователем модели тренда. При вычислениях используется МНК. Модель тренда выбирается из набора, включающего в себя пять наиболее распространённых аналитических моделей: линейную, логарифмическую, полиноминальную (параболическую), степенную, экспоненциальную и модель адаптивной скользящей средней (формулы см. выше данном разделе). Параметры аналитических моделей вычисляются по данным наблюдения, по которым построен график динамического ряда. В результате реализации процедуры в область построения графика выводятся график функции тренда, её аналитическое выражение и значение коэффициента детерминации R 2 . При изменении любых значений исходного ряда динамики процедура автоматически пересчитывает и обновляет параметры линии тренда и её график.
Для доступа к процедуре Добавить линию тренда необходимо:
1. В диапазон ячеек определённого столбца ввести уровни исследуемого динамического ряда.
2. С помощью Мастера Функций построить диаграмму (график) ряда динамики.
3. Щелчком на диаграмме активизировать её. На панели меню на месте пункта Данные появится пункт Диаграмма.
4. В пункте меню Диаграмма выбрать команду Добавить линию тренда. Откроется диалоговое окно Линия тренда.
5. В открывшемся окне Линия тренда раскрыть вкладку Тип.
6. На этой вкладке в разделе Построение линии тренда (аппроксимация и сглаживание) выбрать тип (вид) функции тренда.
7. В списке Построен на ряде выделить ряд данных, для которых строится линия тренда.
8. Раскрыть вкладку Параметры диалогового окна Линия тренда.
Эта вкладка содержит следующие элементы управления:
группу переключателей Название аппроксимирующей (глаженной) кривой, состоящую из двух переключателей. При установке переключателя автоматическое Excel автоматически присваивает линии тренда имя, связанное с типом этой линии и названием данных наблюдения, по которым строится линия тренда, например, Линейный (Урожайность зерновых). При установке переключателя другое пользователь сам устанавливает имя линии регрессии и вводит это имя в поле Линейный (Ряд 1), расположенное справа от переключателя (максимальная длина имени 256 символов);
группу счётчиков Прогноз, в которую входят два счётчика: вперёд на…единиц и назад на…единиц. С помощью этих счётчиков устанавливается срок прогноза и производится экстраполяция и интерполяция ряда динамики. Счётчики недоступны в режиме Скользящее среднее;
флажок пересечение кривой с осью Y в точке. Если этот флажок не установлен, ордината точки пересечения линии тренда с осью Y вычисляется по данным наблюдения. Как правило, этот флажок не устанавливается. Используя этот флажок и расположенное справа от него поле ввода, можно задать нужную ординату точки пересечения (при активном флажке и нуле в поле ввода линия тренда пройдет через начало координат);
флажок показывать уравнение на диаграмме. При установке этого флажка в область построения диаграммы выводится аналитическое выражение (формула) функции тренда;
флажок поместить на диаграмму величину достоверности аппроксимации. При установке этого флажка в область построения диаграммы выводится значение коэффициента детерминации R 2 , который показывает, на сколько процентов выбранная линия тренда объясняет разброс уровней ряда. Чем больше данный показатель, тем более точно выбрана линия тренда. Сравнивая величину R 2 по разным аналитическим моделям можно определить аппроксимирующую функцию. то есть наиболее точно описывающую основную тенденцию развития изучаемого явления.
9. Установить нужные переключатели, счётчики и флажки. Щёлкнуть на кнопке ОК.
Список рекомендуемой литературы
1. Вадзинский Р. Статистические вычисления в среде Еxcel. –СПб.: Питер,2008.
2. Макарова Н.В. Трофимец В.Я. Статистика в Еxcel.– М.: Финансы и статитсика, 2006.
3. Берк К. Кэйри П. Анализ данных с помощью MS Еxcel.–М.: Вильямс, 2005.
4. Васильев А.Н. Научные вычисления в Microsoft Excel.–М.; Спб.; Киев: Диалектика, 2004.
5.Вуколов Э.А. Основы статистического анализа: практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и Еxcel.– М.: Форум; Инфра–М, 2004.
6. Минько А.А. Статистический анализ в среде Еxcel.–М., СПб., Киев: Диалектика, 2004.
7. Гайдышев И. Анализ и обработка данных.–СПб; М.: Питер, 2001.
8. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. М: Финансы и статистика, 2005
9. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА- М, 2006.
10. Теория статистики: Учебник / Под ред. Р.А. Шмойловой .4-е изд., доп. и перераб. — М.: Финансы и статистика, 2005.
11. Теория статистики: Учебник/ Под ред. Г.Л. Громыко.- ИНФРА- М, 2006.
Источник