-
Формируемые
навыки и умения:—
освоение методики анализа статистических
данных;—
освоение методики прогнозирования
значений экономических показателей
с помощью функций и пакета анализа
MS
Excel;—
изучение и освоение методики проведения
корреляционного и регрессионного
анализа.
Теоретическая
поддержка
Наиболее
широкое распространение при построении
прогнозов развития в практике коммерческой
деятельности получили экономико-статистические
модели,
которые описывают зависимость исследуемого
экономического показателя от одного
или нескольких факторов, оказывающих
на него существенное влияние.
MS
Excel
предлагает широкий диапазон средств
для изучения экономической информации.
Множество встроенных статистических
функций (СРЗНАЧ, МЕДИАНА, МОДА и др.)
используют для проведения несложного
анализа данных.
Если
возможностей встроенных функций
недостаточно, то обращаются к
инструменту Описательная
статистика,
имеющийся в пакете «Статистический
анализ» MS
Excel.
Выходной диапазон инструмента Описательная
статистика
содержит следующие статистические
характеристики для каждой переменной
из входного диапазона: среднее, стандартная
ошибка, медиана, мода, стандартное
отклонение, дисперсия и др.
Корреляционный
анализ –
это раздел математической статистики,
посвященный изучению взаимосвязей
между случайными величинами. Основной
целью корреляционного анализа
является установление характера
влияния факторной переменной на
исследуемый показатель и определение
тесноты их связи с тем, чтобы с достаточной
степенью надежности строить модель
развития исследуемого показателя.
С
технической точки зрения проведение
корреляционного анализа сводится к
расчету коэффициентов парной корреляции,
значения которых помогут судить о
характере и тесноте связи между
исследуемым показателем и каждой
отобранной факторной переменной.
Коэффициент
парной корреляции
используется в качестве меры,
характеризующей степень линейной связи
двух переменных. Значение коэффициента
корреляции лежит в интервале от -1 (в
случае строгой линейной отрицательной
связи) до +1 (в случае строгой линейной
положительной связи). Соответственно,
положительное значение коэффициента
корреляции свидетельствует о прямой
связи между исследуемым и факторным
показателем, а отрицательное — об
обратной. Чем ближе значение коэффициента
корреляции к 1, тем теснее связь.
Качественно оценить тесноту связи
позволяет специальная шкала значений
коэффициентов корреляции, разработанная
профессором Колумбийского университета
США Чеддоком (таблица 3.1).
Таблица 3.1 — Шкала
значений коэффициентов корреляции
|
Размер |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
|
Теснота связи |
слабая |
умеренная |
заметная |
высокая |
весьма высокая |
Для
количественной оценки взаимосвязи двух
наборов данных можно обратиться к
статистической функции КОРРЕЛ, вызывая
ее в диалоговом окне Мастера
функций.
Однако
чаще всего в экономических расчетах
приходится иметь дело сразу с несколькими
(более двух) наборами данных, взаимосвязи
которых требуется изучить. В этом случае
рассчитывают коэффициент
множественной корреляции, который
принимает значения от 0 до 1, но несет
в себе более универсальный смысл:
чем ближе его значение к 1, тем в большей
степени учтены факторы, влияющие на
зависимую переменную, тем более точной
выглядит построенная на основе отобранных
факторов модель.
В
таких случаях обращаются к инструменту
Корреляция,
содержащемуся в пакете «Статистический
анализ» Excel.
Для этого используют команду Анализ
данных из
меню Сервис.
В открывшемся окне Инструменты
анализа
вызывают инструмент Корреляция.
Регрессионный
анализ имеет
своей целью вывод, определение
(идентификацию) уравнения регрессии,
включая статистическую оценку его
параметров.
В
основе любой регрессионной модели
лежит уравнение (или система уравнений)
регрессии, которое показывает, каким
будет в среднем изменение зависимой
переменной у,
если независимые переменные х
примут конкретные значения. Это
обстоятельство позволяет применять
модель регрессии не только для анализа,
но и для прогнозирования.
Методика
построения и виды моделей тренда. Если
имеется некоторая совокупность данных,
характеризующих динамику исследуемого
показателя, то всегда можно попытаться
найти на графике наилучшую линию,
которая будет «ближайшей» к точкам
наблюдений в рамках всей их совокупности.
Чтобы составить прогноз развития
исследуемого показателя, используя
линии тренда Excel,
сначала необходимо с помощью Мастера
диаграмм
построить диаграмму его динамики на
основе базовых данных. Когда диаграмма
построена, открывается контекстное
меню, в котором содержится команда
«Добавить
линию тренда».
После ее выбора Excel
выведет окно диалога Линии
тренда,
содержащее две основные вкладки: Тип
и Параметры.
Прогнозирование
с применением функции экспоненциального
сглаживания. Для
составления прогнозов методом
экспоненциального сглаживания в Excel
предусмотрен инструмент Экспоненциальное
сглаживание.
Активизировать инструмент
Экспоненциальное
сглаживание
можно из меню Сервис
после загрузки надстройки Пакет
анализа
посредством команды Анализ
данных.
Инструмент Экспоненциальное
сглаживание
целесообразно применять для составления
прогнозов только на период, непосредственно
следующий за интервалом базовых
наблюдений.
Вычисление
скользящего среднего средствами Excel.
Инструмент
Скользящее
среднее
можно вызвать в диалоговом окне команды
Анализ данных
из меню Сервис.
Как правило, прогноз с применением
скользящего среднего составляется
на период, непосредственно следующий
за интервалом наблюдения.
Составление
линейных прогнозов средствами Excel
Функция рабочего
листа ЛИНЕЙН помогает определить
характер линейной связи между результатами
наблюдений и временем их фиксации и
дать ей математическое описание,
наилучшим образом аппроксимирующее
исходные данные.
Функция
ТЕНДЕНЦИЯ рассчитывает прогнозные
значения исследуемого показателя в
соответствии с линейным трендом.
Функция
ПРЕДСКАЗ аналогична функции ТЕНДЕНЦИЯ
за исключением того, что она определяет
лишь одну точку на линии тренда и не
может рассчитать массив, который
формирует эту линию. Поэтому ее удобно
использовать для оперативного вычисления
единичных прогнозов.
Использование
возможностей Excel
при построении нелинейных прогнозов
Функция
ЛГРФПРИБЛ работает подобно функции
ЛИНЕЙН. Различия между ними состоят
лишь в том, что ЛИНЕЙН определяет
параметры прямой линии, наилучшим
образом аппроксимирующей исходные
данные, а функция ЛГРФПРИБЛ —
экспоненциальной кривой.
В
то время как функция ЛГРФПРИБЛ рассчитывает
параметры уравнения экспоненциальной
кривой роста, которая аппроксимирует
наилучшим образом множество базовых
данных, функция РОСТ определяет точки,
лежащие на этой кривой.
Вызвать
функции ЛИНЕЙН, ТЕНДЕНЦИЯ, ПРЕДСКАЗ,
ЛГРФПРИБЛ и РОСТ можно в диалоговом
окне Мастера
функций
(категория «Статистические»), расположенном
на панели инструментов Стандартная.
Задание
1. Использование инструмента Описательная
статистика
В
рамках оценки конкурентоспособности
гастронома исследовать центральную
тенденцию и изменчивость уровня
рентабельности двадцати продовольственных
магазинов (гастрономов) области на
основе следующих собранных по ним
за отчетный период данных (таблица 3.2).
Таблица
3.2 — Данные об уровне рентабельности по
магазинам (гастрономам) области за
отчетный период
|
А |
В |
С |
D |
Е |
F |
G |
Н |
|
|
1 |
№ п/п |
Уровень |
||||||
|
2 |
1 |
0,94 |
||||||
|
3 |
2 |
1,22 |
||||||
|
4 |
3 |
0,8 |
||||||
|
5 |
4 |
1,67 |
||||||
|
6 |
5 |
1,56 |
||||||
|
7 |
6 |
0,94 |
||||||
|
8 |
7 |
1,23 |
||||||
|
9 |
8 |
0,87 |
||||||
|
10 |
9 |
1,22 |
||||||
|
11 |
10 |
1,43 |
||||||
|
12 |
11 |
0,16 |
||||||
|
13 |
12 |
0,44 |
||||||
|
14 |
13 |
0,8 |
||||||
|
15 |
14 |
1,03 |
||||||
|
16 |
15 |
0,55 |
||||||
|
17 |
16 |
1,22 |
||||||
|
18 |
17 |
1,17 |
||||||
|
19 |
18 |
0,02 |
||||||
|
20 |
19 |
0,28 |
||||||
|
21 |
20 |
1,22 |
Выполнение:
Порядок
обработки ряда данных с помощью
инструмента Описательная статистика
установлен в диалоговом окне Описательная
статистика,
которое можно вызвать из меню Сервис
через команду Анализ
данных.
Открывшееся окно диалога предлагает
пользователю определиться с набором
следующих параметров (рисунок 3.1):
1)
Входной
диапазон
(интервал) — предполагает ввод ссылки
на ячейки рабочего листа, которые
содержат анализируемые данные. Тогда
входной диапазон объединяет ячейки
В1:В21;
2)
Группирование
— требует установления переключателя
в положение «По столбцам» или «По
строкам» в зависимости от расположения
данных во входном диапазоне. Поскольку
данные об уровне рентабельности
расположены в таблице 3.2 в виде столбца,
то переключатель следует установить
в положение «По столбцам»;
3)
Метки в первой
строке/Метки в первом столбце
— позволяет определить название каждого
столбца (или строки) выходной таблицы.
Переключатель устанавливается в
положение «Метки в первой строке», если
первая строка во входном диапазоне
содержит названия столбцов. Когда в
первом столбце входного диапазона
находятся названия строк, переключатель
устанавливается в положение «Метки в
первом столбце». Если входной диапазон
не содержит меток, то необходимые
заголовки в выходном диапазоне создаются
на основе программы автоматически.
Учитывая, что в таблице 3.2 первая строка
содержит названия столбцов, переключатель
следует установить в положение «Метки
в первой строке»;
4)
Уровень
надежности
— используется, если в выходную
таблицу необходимо включить строку для
уровня надежности. Тогда в соответствующее
поле диалогового окна вводится требуемое
значение. В экономических расчетах, как
правило, значения уровня надежности
задают в размере 95 или 99 %. Например,
значение 95 % вычисляет уровень надежности
среднего со значимостью 0,05;
5)
К-й наибольший
— применяется, если в выходную таблицу
необходимо включить строку для k-го
наибольшего значения входного диапазона
данных. В соответствующем окне вводится
число k.
Если k
равно 1, эта строка будет содержать
максимум из набора данных. Например,
при оценке конкурентоспособности нашего
гастронома (пусть в таблице 3.2 он имеет
порядковый номер 7) для нас важно
проследить, попал ли уровень его
рентабельности в первую тройку наиболее
высокорентабельных предприятий, а
также, каков диапазон изменения уровня
рентабельности у трех самых
высокорентабельных магазинов. Тогда
для k-го
наибольшего в диалоговом окне надо
ввести цифру 3 (т.е. k
= 3). Это значит, что в выходной таблице,
кроме максимального значения уровня
рентабельности, будет отражен третий
за ним по убывающей размер уровня
рентабельности из всей исследуемой
совокупности данных;
6)
К-й наименьший
— применяется, если в выходную таблицу
необходимо включить строку для k-го
наименьшего значения входного диапазона
данных. В соответствующем окне вводится
число k.
Если k
равно 1, эта строка будет содержать
минимум из набора данных. Например, для
нас важно убедиться, что уровень
рентабельности исследуемого гастронома
не относится к пяти самым низким
показателям. Тогда в диалоговом окне
для k-го
наименьшего вводится цифра 5. Это значит,
что в выходной таблице, кроме минимального
значения уровня рентабельности, будет
отражен пятый за ним по возрастающей
размер уровня рентабельности;
7)
Выходной
диапазон —
предполагает введение ссылки на левую
верхнюю ячейку выходного диапазона.
Инструмент Описательная статистика
выводит два столбца сведений для
каждого набора данных. Левый столбец
содержит наименования рассчитанных
статистических величин, а правый —
их значения. В нашем случае выходная
таблица статистических характеристик
должна быть расположена, например, на
том же рабочем листе, что и входная, на
одном с ней уровне, но правее. Тогда
можно задать следующий выходной
диапазон — D1;

Новый лист
— применяют, чтобы открыть новый лист
в книге и вставить результаты анализа,
начиная с ячейки А1. При необходимости
в поле диалогового окна, расположенном
напротив соответствующего положения
переключателя, вводится имя нового
листа;
9)
Новая книга
— используется, когда необходимо
открыть новую книгу и вставить
результаты анализа в ячейку А1 на первом
листе этой книги;
10)
Итоговая
статистика
— требует установления флажка, который
означает, что в выходном диапазоне
необходимо получить полный список
статистических характеристик:
Среднее, Стандартная ошибка (среднего),
Медиана, Мода, Стандартное отклонение,
Дисперсия выборки, Эксцесс,
Асимметричность, Интервал, Минимум,
Максимум, Сумма, Счет, Наибольшее (k-e),
Наименьшее (k-e),
Уровень надежности.
Рисунок
3.1 — Окно диалога Описательная
статистика
Проведение
всех вышеобозначенных действий с данными
таблицы 3.2 позволяет получить следующую
итоговую таблицу обобщенных статистических
характеристик уровня рентабельности
исследуемых торговых предприятий
(таблица 3.3).
Таблица
3.3 — Статистическая оценка данных об
уровне рентабельности по магазинам
(гастрономам) области за отчетный год
|
А |
В |
С |
D |
Е |
|
|
1 |
№ п/п |
Уровень |
Результат |
||
|
2 |
1 |
0,94 |
|||
|
3 |
2 |
1,22 |
Среднее |
0,9385 |
|
|
4 |
3 |
0,8 |
Стандартная |
0,10199 |
|
|
5 |
4 |
1,67 |
Медиана |
0,985 |
|
|
6 |
5 |
1,56 |
Мода |
1,22 |
|
|
7 |
6 |
0,94 |
Стандартное |
0,45611 |
Продолжение
таблицы 3.3
|
А |
В |
С |
D |
Е |
|
|
1 |
№ п/п |
Уровень |
Результат |
||
|
8 |
7 |
1,23 |
Дисперсия выборки |
0,20803 |
|
|
9 |
8 |
0,87 |
Эксцесс |
-0,3986 |
|
|
10 |
9 |
1,22 |
Асимметричность |
-0,5196 |
|
|
11 |
10 |
1,43 |
Интервал |
1,65 |
|
|
12 |
11 |
0,16 |
Минимум |
0,02 |
|
|
13 |
12 |
0,44 |
Максимум |
1,67 |
|
|
14 |
13 |
0,8 |
Сумма |
18,77 |
|
|
15 |
14 |
1,03 |
Счет |
20 |
|
|
16 |
15 |
0,55 |
Наибольший(5) |
1,22 |
|
|
17 |
16 |
1,22 |
Наименьший(3) |
0,28 |
|
|
18 |
17 |
1,17 |
Уровень |
0,21347 |
|
|
19 |
18 |
0,02 |
|||
|
20 |
19 |
0,28 |
|||
|
21 |
20 |
1,22 |
Вывод:
Приведенные в таблице 3.3 данные позволяют
оперативно проследить, что уровень
рентабельности по двадцати исследуемым
предприятиям за анализируемый период
сложился в среднем 0,94+0,46
% и колебался в пределах 0,02-1,67 %.
С известной долей
условности можно предположить, что
приблизительно 68 % магазинов имели
уровень рентабельности между 0,48%
(0,94 — 0,46) и 1,4% (0,94 + 0,46).
Стандартное
отклонение (± 0,456) свидетельствует о
достаточно сильном разбросе размеров
уровня рентабельности предприятий
относительно его среднего значения,
т.е. отобранные магазины далеко не в
равной степени могут рассматриваться
в качестве конкурентов нашего предприятия.
Исследуемый
гастроном № 7, имея уровень рентабельности
1,23 %, не относится к тройке самых
высокорентабельных предприятий
(1,43-1,67 %), но, судя по медиане, принадлежит
к той половине предприятий, которая
обладает большей рентабельностью. Чаще
всего в выборке присутствует уровень
рентабельности 1,22 % (что тоже ниже
показателя нашего гастронома), а
отрицательное значение коэффициента
асимметрии свидетельствует о более
высокой плотности распределения
значений уровня рентабельности, больших
величины 1,22 % (левосторонней асимметрии).
Следовательно, по показателю рентабельности
у гастронома № 7 гораздо меньше реальных
конкурентов, чем общее количество
членов выборки. При этом рассчитанные
коэффициенты асимметрии и эксцесса
указывают на неоднородность исследуемого
массива данных и необходимость пересмотра
его состава. В этой связи для проведения
углубленного анализа реальных
конкурентов магазина № 7 по избранному
признаку целесообразно пересмотреть
и урезать выборку.
Задание
2. Проведение корреляционного анализа
Провести
корреляционный анализ товарооборота
на основе информации, подготовленной
с помощью электронных таблиц Excel
(таблица 3.4).
Для
проведения корреляционного анализа
объема товарооборота (исследуемый
показатель) могут быть отобраны следующие
факторы:
— товарооборачиваемость
в днях;
— удельный вес
торговой площади в общей площади
предприятия;
—
удельный вес торгово-оперативных
работников в их общей численности;
—
удельный вес товаров с высоким (в рамках
установленного действующим
законодательством предельного уровня)
уровнем торговых надбавок.
Таблица
3.4 — Исходные данные для проведения
корреляционного анализа
|
А |
В |
С |
D |
Е |
F |
|
|
1 |
||||||
|
2 |
Порядковый |
Объем |
Оборачиваемость дни |
Удельный |
Удельный |
Удельный |
|
3 |
1 |
28415 |
43,5 |
44,0 |
67,7 |
22,5 |
|
4 |
2 |
28231 |
43,0 |
44,0 |
67,7 |
18,0 |
|
5 |
3 |
29783 |
43,0 |
44,0 |
70,2 |
24,9 |
|
6 |
4 |
30969 |
43,5 |
47,8 |
70,0 |
24,4 |
|
7 |
5 |
30494 |
43,0 |
47,8 |
68,0 |
20,6 |
|
8 |
6 |
29757 |
42,5 |
47,8 |
68,0 |
19,0 |
|
9 |
7 |
30850 |
43,0 |
49,0 |
70,2 |
22,2 |
|
10 |
8 |
31325 |
41,5 |
49,0 |
70,0 |
21,6 |
|
11 |
9 |
31359 |
42,0 |
50,3 |
70,0 |
19,8 |
|
12 |
10 |
31610 |
41,5 |
50,3 |
70,0 |
19,7 |
|
13 |
11 |
32366 |
40,5 |
50,3 |
70,0 |
23,1 |
|
14 |
12 |
33313 |
40,0 |
50,3 |
70,0 |
23,9 |
|
15 |
13 |
33508 |
40,0 |
50,3 |
68,0 |
21,2 |
|
16 |
14 |
33374 |
39,0 |
50,3 |
68,0 |
20,4 |
|
17 |
15 |
34811 |
39,5 |
50,3 |
70,0 |
24,2 |
|
18 |
16 |
36046 |
39,0 |
49,0 |
70,0 |
26,5 |
Выполнение:
Для
количественной оценки взаимосвязи
объема данных обращаются к инструменту
Корреляция,
содержащемуся в пакете «Статистический
анализ» Excel.
Для этого используют команду Анализ
данных из
меню Сервис.
В открывшемся окне Инструменты
анализа
вызывают инструмент Корреляция,
диалоговое окно которого предлагает
пользователю определить следующие
параметры (рисунок 3.2):
1)
Входной
диапазон (интервал)
— предполагает ввод ссылки на ячейки
рабочего листа, которые содержат
анализируемые данные. Для данных
таблицы 3.4 входной диапазон имеет
вид — B2:F18;
2)
Группирование
— требует установления переключателя
в положение «По столбцам» или «По
строкам» в зависимости от расположения
данных во входном диапазоне. Поскольку
анализируемые наборы данных расположены
в таблице 3.4 в виде столбцов, то
переключатель следует установить в
положение «По столбцам»;
3)
Метки в первой
строке/Метки в первом столбце
— позволяет определить название каждого
столбца (или строки) выходной таблицы.
Переключатель устанавливается в
положение «Метки в первой строке», если
первая строка во входном диапазоне
содержит названия столбцов. Когда в
первом столбце входного диапазона
находятся названия строк, переключатель
устанавливается в положение «Метки в
первом столбце». Если входной диапазон
не содержит меток, то необходимые
заголовки в выходном диапазоне создаются
на основе программы автоматически.
Учитывая, что в таблице 3.4 первая строка
содержит названия столбцов, переключатель
следует установить в положение «Метки
в первой строке»;
4)
Выходной
диапазон —
предполагает введение ссылки на левую
верхнюю ячейку выходного диапазона.
Например, если необходимо, чтобы выходная
таблица располагалась на том же рабочем
листе, что и входная, и непосредственно
под ней, то можно задать выходной диапазон
ячейкой А21;
5)
Новый лист
— применяют, чтобы открыть новый лист
в книге и вставить результаты анализа,
начиная с ячейки А1. При необходимости
в поле диалогового окна, расположенном
напротив соответствующего положения
переключателя, вводится имя нового
листа;
6)
Новая книга
— используется, когда необходимо
открыть новую книгу и вставить
результаты анализа в ячейку А1 на первом
листе этой книги.
Рисунок
3.2 — Окно диалога Корреляция
Проведение
всех обозначенных действий с данными
таблицы 3.4 позволяет получить матрицу
значений парных коэффициентов
корреляции, рассчитанных для всех
возможных пар переменных без учета
влияния других факторов (таблица 3.5).
Поскольку коэффициент корреляции двух
наборов данных не зависит от
последовательности их обработки, то
выходная область занимает только
половину предназначенного для нее
места. Ячейки выходного диапазона,
имеющие совпадающие координаты строк
и столбцов, содержат значение 1, так как
каждая строка или столбец во входном
диапазоне полностью коррелирует с самим
собой.
Таблица
3.5 — Матрица парных коэффициентов
корреляции
|
А |
В |
С |
D |
E |
F |
|
|
21 |
Объем товарооборота, |
Оборачиваемость |
Удельный вес |
Удельный вес |
Удельный вес |
|
|
22 |
Объем товарооборота, |
1 |
||||
|
23 |
Оборачиваемость |
-0,90538094 |
1 |
|||
|
24 |
Удельный вес |
0,75014268 |
-0,690531 |
1 |
||
|
25 |
Удельный вес |
0,38663194 |
-0,153964 |
0,3726409 |
1 |
|
|
26 |
Удельный вес |
0,50878765 |
-0,276455 |
0,0374572 |
0,580400123 |
1 |
Вывод:
На основе приведенной матрицы можно
содержательно оценить связь значений
объема товарооборота с каждым из
отобранных факторов и выбрать наиболее
значимые из них для включения в модель.
Так, полученные коэффициенты корреляции,
характеризующие тесноту связи объема
товарооборота с отобранными факторами
(см. столбец В21:В26 таблицы 3.5), составляют
соответственно: -0,905 для фактора
«оборачиваемость товаров»; 0,750 для
фактора «удельный вес торговой площади
в общей»; 0,509 для фактора «удельный вес
товаров с высокими торговыми надбавками»;
0,387 для фактора «удельный вес
торгово-оперативного персонала в общей
численности работников». Согласно шкале
Чеддока (таблица 3.1), для данного торгового
предприятия показатель объема
товарооборота имеет весьма высокую
тесноту связи с фактором «оборачиваемость
товаров» и высокую — с фактором
«удельный вес торговой площади в
общей». Значение коэффициента корреляции,
рассчитанное для товарооборота и фактора
«удельный вес торгово-оперативного
персонала», свидетельствует о слабо
выраженной линейной связи между
этими показателями.
Знак
«-» перед коэффициентом корреляции в
ячейке В23 означает, что между объемом
товарооборота и размером товарооборачиваемости
в днях имеет место обратная связь, т.е.
при росте количества дней одного оборота
товарного запаса предприятия в днях
(иными словами — замедлении
товарооборачиваемости) объем его
реализации при прочих равных условиях
будет падать. С остальными факторами
объем товарооборота находится в
прямой зависимости.
Задание
3. Прогнозирование развития показателей
с помощью линии тренда Excel
Составить
прогноз товарооборота торгового
предприятия на 17-й месяц (см. данные
таблицы 3.6) с помощью команды Добавить
линию тренда.
Таблица 3.6 — Сведения
о динамике товарооборота торгового
предприятия
|
А |
В |
С |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый номер |
Объем |
||||
|
3 |
1 |
28415 |
||||
|
4 |
2 |
28231 |
||||
|
5 |
3 |
29783 |
||||
|
6 |
4 |
30969 |
||||
|
7 |
5 |
30494 |
||||
|
8 |
6 |
29757 |
||||
|
9 |
7 |
30850 |
||||
|
10 |
8 |
31325 |
||||
|
11 |
9 |
31359 |
||||
|
12 |
10 |
31610 |
||||
|
13 |
11 |
32366 |
||||
|
14 |
12 |
33313 |
||||
|
15 |
13 |
33508 |
||||
|
16 |
14 |
33374 |
||||
|
17 |
15 |
34811 |
||||
|
18 |
16 |
36046 |
||||
|
19 |
Итого |
Выполнение:
Чтобы
составить прогноз развития исследуемого
показателя, используя линии тренда
Excel,
сначала необходимо с помощью Мастера
диаграмм
построить диаграмму (График)
его динамики на основе базовых данных
(ячейки В3:В19 таблицы 3.6).
Когда
диаграмма построена, необходимо щелкнуть
правой клавишей мыши на любой точке
графика, чтобы открылось контекстное
меню, в котором содержится команда
Добавить
линию тренда.
После ее выбора Excel
выведет окно диалога Линии
тренда,
содержащее две основные вкладки: Тип
и Параметры.
Вкладка
Тип
помогает пользователю выбрать тип линии
тренда, которая будет аппроксимировать
исходные данные. В диалоговом окне
предлагается пять типов линий тренда.
Для их построения Excel
использует модели следующего вида:
—
линейную (у
= mх
+ b);
—
полиномиальную (у
= b
+ m1x
+ m2x2
+…+ m6х6);
—
логарифмическую (у
= m
· ln
x
+ b);
—
экспоненциальную (у
= m
· еb·x);
—
степенную (у
= m
· хb).
После
задания типа линии тренда выделяют
вкладку Параметры.
Откроется ее окно диалога, в котором
пользователь определяет следующие
важные моменты:
1)
количество прогнозируемых периодов и
направление прогноза: вперед или назад;
2)
когда выбрана линейная, полиномиальная
или экспоненциальная кривая роста,
то в поле Пересечение
кривой с осью у в точке 0
задается ее у-пересечение:
если данное поле обозначить флажком,
то Excel
будет искать лучшее уравнение кривой,
которая на координатной плоскости
обязательно должна пройти через
начало координат;
3)
через установку флажка в соответствующих
полях окна диалога пользователь
решает, отражать ли на выходной диаграмме
уравнение, на основе которого была
построена линия тренда, и размер
квадрата коэффициента корреляции r2,
характеризующий качество аппроксимации.
C
помощью команды Добавить
линию тренда
составим сразу пять различных вариантов
прогноза товарооборота торгового
предприятия на 17-й месяц и при этом
по r2
оценить общее качество моделей, на
основе которых они были получены.
Используя
возможности Excel
по созданию в ячейках рабочего листа
формул, с помощью приведенных на графиках
уравнений кривых роста рассчитаем
значения прогноза товарооборота на
17-й месяц (таблица 3.7).
Таблица
3.7 — Прогноз товарооборота на 17-й месяц
|
Тип |
Формула |
Прогноз |
|
Линейная |
=437,43*17+27920 |
35356,3 |
|
Логарифмическая |
=2429,4*ln(17)+26981 |
33864,0 |
|
Полиномиальная |
=3,9737*17^3-88,245*17^2+925,09*17+27432 |
1 37178,5 |
|
Степенная |
=27215*17^0,0774 |
33887,9 |
|
Экспоненциальная |
=28081*е^(0,0138*17) |
35490,0 |
|
Рисунок |
Рисунок |
|
Рисунок |
Рисунок |
|
Рисунок |
Рисунок |
Вывод:
Приведенные на рисунках 3.3–3.8 графики
динамики товарооборота свидетельствуют,
что наибольшая степень приближения
линии тренда к базовым данным достигнута
в случае полиномиальной кривой роста
3-й степени (см. рисунок 3.6, r2
= 0,9519), наименьшая — в случае логарифмической
кривой (см. рисунок 3.5, r2
= 0,7779).
Задание
4. Прогнозирование с применением функции
экспоненциального сглаживания
Составить
прогноз товарооборота торгового
предприятия на основе данных таблицы
3.6 с помощью инструмента Экспоненциальное
сглаживание.
Выполнение:
Активизировать
инструмент Экспоненциальное
сглаживание
можно из меню Сервис
после загрузки надстройки Пакет
анализа
посредством команды Анализ
данных.
Открывшееся окно диалога Экспоненциальное
сглаживание
предлагает пользователю определиться
со следующими параметрами (рисунок
3.9):
1)
Входной
диапазон —
требует ссылки на ячейки, содержащие
данные об исследуемом показателе. Этот
диапазон должен состоять из одного
столбца или одной строки и содержать
данные как минимум в четырех ячейках.
В нашем примере параметр Входной
диапазон
включает ячейки В2:В19 (таблица 3.8);
2)
Фактор
затухания
— это корректировочный фактор,
минимизирующий нестабильность
совокупности данных. Он может иметь
значения в пределах от 0 до 1. По умолчанию
пользователя Excel
самостоятельно принимает значение
фактора затухания равным 0,3. В нашем
примере для параметра Фактор
затухания
введем значение 0,1;
3)
Метки
— требует установки флажка, если первая
строка или первый столбец входного
диапазона содержит заголовки (название
столбца или строки). В нашем примере
установим флажок для параметра Метки;
4)
Выходной
диапазон —
предполагает ссылку на верхнюю ячейку
выходного диапазона. В нашем примере
установим верхнюю ячейку Выходного
диапазона – С3;
5)
Вывод графика
— требует установки флажка, если
пользователю, кроме значения прогноза,
необходимо получить встроенную
диаграмму динамики фактических и
расчетных значений;
6)
Стандартные
погрешности
— требует установки флажка, если
пользователю для проведения оценки
качества прогнозов необходимо
включить в выходной диапазон столбец
со стандартными погрешностями e(t).
Рисунок 3.9 — Окно
диалога «Экспоненциальное сглаживание»
В
результате работы инструмента
Экспоненциальное
сглаживание
получаем следующие сглаженные показатели
товарооборота (см. столбец С таблицы
3.8), в том числе прогноз на 17-й месяц —
35 908 ден. ед.
Таблица
3.8 — Расчет прогноза товарооборота с
помощью инструмента Экспоненциальное
сглаживание
|
А |
В |
С |
|||||||
|
1 |
|||||||||
|
2 |
Порядковый |
Объем |
Экспоненциальное |
||||||
|
3 |
1 |
28415 |
#Н/Д |
|
|||||
|
4 |
2 |
28231 |
28415 |
||||||
|
5 |
3 |
29783 |
28249,4 |
||||||
|
6 |
4 |
30969 |
29629,6 |
||||||
|
7 |
5 |
30494 |
30835,1 |
||||||
|
8 |
6 |
29757 |
30528,1 |
||||||
|
9 |
7 |
30850 |
29834,1 |
||||||
|
10 |
8 |
31325 |
30748,4 |
||||||
|
11 |
9 |
31359 |
31267,3 |
||||||
|
12 |
10 |
31610 |
31349,8 |
||||||
|
13 |
11 |
32366 |
31584,0 |
||||||
|
14 |
12 |
33313 |
32287,8 |
||||||
|
15 |
13 |
33508 |
33210,5 |
||||||
|
16 |
14 |
33374 |
33478,2 |
||||||
|
17 |
15 |
34811 |
33384,4 |
||||||
|
18 |
16 |
36046 |
34668,3 |
||||||
|
19 |
17 |
35908,2 |
Задание
5. Прогнозирование с применением метода
скользящего среднего
5.1
При исследовании спроса на реализуемый
товар-новинку в фирменном магазине
в течение 20 дней было зафиксировано
определенное количество поступивших
на него жалоб со стороны покупателей
(таблица 3.9, ячейки В2:В21). Выяснить,
существует ли какая-либо тенденция
поступления жалоб с помощью инструмента
Скользящее
среднее.
Выполнение:
Инструмент
Скользящее
среднее
можно вызвать в диалоговом окне команды
Анализ данных
из меню Сервис.
Открывшееся окно диалога предлагает
пользователю задать следующие
основные параметры (рисунок 3.10):
1)
Входной
диапазон (интервал) — это
диапазон ячеек В2:В21 (см. таблицу 3.9);
2)
Интервал
усреднения
примем равным 3, т.е. будем определять
трехдневное скользящее среднее;
3)
Выходной
диапазон (интервал)
задаем именем ячейки С2. При этом
следует иметь в виду, что первые несколько
ячеек выходного диапазона будут всегда
содержать значение #Н/Д. Количество
таких ячеек равно значению выбранного
интервала усреднения минус один. Эта
ситуация связана с недостаточным
количеством базовых данных для вычисления
среднего значения первых результатов
наблюдений;
4)
Вывод графика
— требует установки флажка, который
означает, что пользователю, кроме
выходного массива (в нашем примере
— в столбце С), необходимо получить
график, который наглядно демонстрирует
линию тренда скользящего среднего.
Если флажок установлен, то Excel
самостоятельно создает график,
включающий две линии: одна из них строится
на основе базовых данных, другая — по
числовым значениям скользящего среднего.
Рисунок
3.10 — Окно диалога Скользящее
среднее
Таблица
3.9 — Оценка тенденции поведения показателей
исследуемого динамического ряда методом
скользящего среднего
|
А |
В |
С |
||
|
1 |
День |
Количество |
|
|
|
2 |
1 |
10 |
#Н/Д |
|
|
3 |
2 |
11 |
#Н/Д |
|
|
4 |
3 |
10 |
10,333 |
|
|
5 |
4 |
12 |
11 |
|
|
6 |
5 |
13 |
11,667 |
|
|
7 |
6 |
13 |
12,667 |
|
|
8 |
7 |
13 |
13 |
|
|
9 |
8 |
10 |
12 |
|
|
10 |
9 |
16 |
13 |
|
|
11 |
10 |
9 |
11,667 |
|
|
12 |
11 |
15 |
13,333 |
|
|
13 |
12 |
10 |
11,333 |
|
|
14 |
13 |
15 |
13,333 |
|
|
15 |
14 |
17 |
14 |
|
|
16 |
15 |
12 |
14,667 |
|
|
17 |
16 |
15 |
14,667 |
|
|
18 |
17 |
14 |
13,667 |
|
|
19 |
18 |
18 |
15,667 |
|
|
20 |
19 |
19 |
17 |
|
|
21 |
20 |
15 |
17,333 |
Вывод:
Приведенные в столбце С таблицы 3.9
выходные значения свидетельствуют (и
это наглядно подтверждает рисунок), что
показатель скользящего среднего имеет
тенденцию к увеличению. В данном
случае выявленная тенденция вызывает
опасения относительно дальнейшей судьбы
товара и требует принятия адекватных
мер со стороны его производителя.
5.2
Составить прогноз объема товарооборота
по торговому предприятию на основе
данных таблицы 3.6, используя расчет
скользящего среднего.
Выполнение:
—
на отдельном рабочем листе Excel
составим разработочную таблицу следующего
вида (таблица 3.10);
Таблица
3.10 — Методика составления прогноза
товарооборота на основе скользящего
среднего средствами Excel
(разработочная таблица)
|
А |
В |
С |
D |
Е |
|
|
1 |
|||||
|
2 |
Порядковый |
Объем |
Цепные |
Показатели |
Среднее |
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
|||
|
5 |
3 |
29783 |
|||
|
6 |
4 |
30969 |
|||
|
7 |
5 |
30494 |
|||
|
8 |
6 |
29757 |
|||
|
9 |
7 |
30850 |
|||
|
10 |
8 |
31325 |
|||
|
11 |
9 |
31359 |
|||
|
12 |
10 |
31610 |
|||
|
13 |
11 |
32366 |
|||
|
14 |
12 |
33313 |
|||
|
15 |
13 |
33508 |
|||
|
16 |
14 |
33374 |
|||
|
17 |
15 |
34811 |
|||
|
18 |
16 |
36046 |
—
учитывая, что объем товарооборота
представляет собой абсолютный стоимостный
показатель, для расчета скользящего
среднего создадим в разработочной
таблице колонку относительных величин,
характеризующих динамику товарооборота
предприятия — цепных темпов прироста
(вводим в ячейку С4 формулу =В4/В3*100-100 и
копируем ее в ячейки С5:С18) (столбец С
таблицы 3.10);
—
выравнивание динамического ряда,
состоящего из 15 цепных темпов прироста
товарооборота, проведем, используя
интервал усреднения, равный, например,
5. Для расчета показателей выровненного
ряда (столбец D
таблицы 3.10) воспользуемся другим способом
создания скользящего среднего в Excel,
т.е. прямым введением формулы в
соответствующую ячейку рабочего
листа. Так, чтобы получить пятимесячное
скользящее среднее цепных темпов
прироста, в ячейку D8
таблицы 10 вводится формула =СРЗНАЧ(С4:С8).
Затем эта формула с помощью средства
Автозаполнение
копируется и вставляется в ячейки
D9:D18;
—
для составления прогноза товарооборота
на 17-й месяц в таблице 3.10 необходимо
занести еще три формулы: расчета среднего
изменения темпов его прироста: =(D18-D8)/10
(ячейка Е18), расчета прогнозируемого
цепного темпа прироста на 17-й месяц:
=D18+2*E18
(ячейка С20), расчета прогнозируемого
объема товарооборота: B18*(C20+100)/100
(ячейка В20). Результатом всех проведенных
операций становится итоговая таблица
3.11, содержащая все промежуточные
элементы и значения единой цепи
составления прогноза товарооборота.
Таблица
3.11 — Прогноз товарооборота на основе
скользящего среднего средствами Excel
(итоговая таблица)
|
А |
В |
С |
D |
Е |
|
|
1 |
|||||
|
2 |
Порядковый |
Объем |
Цепные |
Показатели |
Среднее |
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
-0,648 |
#Н/Д |
|
|
5 |
3 |
29783 |
5,498 |
#Н/Д |
|
|
6 |
4 |
30969 |
3,982 |
#Н/Д |
|
|
7 |
5 |
30494 |
-1,534 |
#Н/Д |
|
|
8 |
6 |
29757 |
-2,417 |
0,976 |
|
|
9 |
7 |
30850 |
3,673 |
1,840 |
|
|
10 |
8 |
31325 |
1,540 |
1,049 |
|
|
11 |
9 |
31359 |
0,109 |
0,274 |
|
|
12 |
10 |
31610 |
0,800 |
0,741 |
|
|
13 |
11 |
32366 |
2,392 |
1,703 |
|
|
14 |
12 |
33313 |
2,926 |
1,553 |
|
|
15 |
13 |
33508 |
0,585 |
1,362 |
|
|
16 |
14 |
33374 |
-0,400 |
1,261 |
|
|
17 |
15 |
34811 |
4,306 |
1,962 |
|
|
18 |
16 |
36046 |
3,548 |
2,193 |
0,122 |
|
19 |
Прогноз |
||||
|
20 |
17 |
36924 |
2,436 |
Задание
6. Использование функции ЛИНЕЙН для
создания модели тренда
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ЛИНЕЙН.
Выполнение:
Функция
рабочего листа ЛИНЕЙН помогает определить
характер линейной связи между результатами
наблюдений и временем их фиксации и
дать ей математическое описание,
наилучшим образом аппроксимирующее
исходные данные. Для построения трендовой
модели она использует уравнение вида
у = mх
+ b,
где у
— исследуемый показатель; х
= t
— временной
тренд; b,
m
— параметры уравнения, характеризующие
соответственно у-пересечение
и наклон линии тренда.
Вызвать
функцию ЛИНЕЙН можно в диалоговом окне
Мастера
функций
(категория «Статистические»),
расположенном на панели инструментов
Стандартная.
Используя
метод наименьших квадратов, функция
ЛИНЕЙН создает массив значений, который
описывает искомую модель тренда.
Учитывая, что создается массив значений,
функция должна задаваться пользователем
в виде формулы массива. Поэтому перед
началом работы с ЛИНЕЙН необходимо
на рабочем листе выделить диапазон
ячеек, достаточный для размещения
создаваемого ею массива значений. Так,
для прогнозирования товарооборота по
данным таблицы 3.6 обозначим ячейками
E10:F14
диапазон для формирования выходного
массива (таблица 3.12). После того, как
выделен выходной диапазон и пользователь
определился с аргументами функции
посредством диалогового окна ЛИНЕЙН,
следует нажать на клавиатуре кнопки
Ctrl+Shift+Enter.
Таблица 3.12 — Расчет
и оценка линейной модели тренда с помощью
функции ЛИНЕЙН
|
A |
B |
C |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый |
Объем |
||||
|
3 |
1 |
28415 |
||||
|
4 |
2 |
28231 |
||||
|
5 |
3 |
29783 |
||||
|
6 |
4 |
30969 |
||||
|
7 |
5 |
30494 |
||||
|
8 |
6 |
29757 |
||||
|
9 |
7 |
30850 |
||||
|
10 |
8 |
31325 |
Линейная |
437,425 |
27920,1 |
|
|
11 |
9 |
31359 |
Статистика |
34,958505 |
338,033 |
|
|
12 |
10 |
31610 |
0,917921 |
644,603 |
||
|
13 |
11 |
32366 |
156,56746 |
14 |
||
|
14 |
12 |
33313 |
65055814 |
5817182 |
||
|
15 |
13 |
33508 |
||||
|
16 |
14 |
33374 |
||||
|
17 |
15 |
34811 |
||||
|
18 |
16 |
36046 |
Функция
ЛИНЕЙН имеет четыре аргумента (рисунок
3.11):
1)
Известные
значения у
— это множество уже известных значений
исследуемого показателя, на основе
которых будет производиться оценка
параметров уравнения тренда. Так, при
составлении прогноза товарооборота
торгового предприятия по данным
таблицы 3.6 известные значения у
представлены в виде столбца и находятся
в ячейках В3:В18;
2)
Известные
значения х
— при построении трендовой модели
представляют собой временной ряд,
соответствующий по размерам первому
аргументу. В нашем примере он находится
в ячейках А3:А18 таблицы 3.6 и отражает
порядковые номера месяца;
3)
Конст
— логическое значение, которое указывает
на необходимость расчета параметра b
(свободного члена) при построении модели
тренда. Если Конст
имеет значение ИСТИНА, то параметр b
вычисляется. Если Конст
имеет значение ЛОЖЬ, то параметр b
принимается равным нулю;
4)
Статистика
— логическое значение, которое указывает
на необходимость отражения на рабочем
листе дополнительной статистической
информации, позволяющей судить о качестве
построенной модели. Если этот аргумент
имеет значение ЛОЖЬ или ссылка на
него отсутствует, то функция ЛИНЕЙН не
рассчитывает статистические характеристики.
Если Статистика
задана значением ИСТИНА, то массив,
создаваемый функцией, содержит значения
следующих статистических величин
(таблица 3.13).
Таблица
3.13 — Значения статистических величин
функции ЛИНЕЙН
|
Стандартная |
Стандартная |
|
Квадрат |
Стандартная |
|
F-критерий |
Степень |
|
Сумма |
Остаточная |
Рисунок 3.11 — Окно
диалога функции ЛИНЕЙН
Вывод:
Число в ячейке Е10 представляет собой
наклон линии тренда (m
= 437,425), а
число в ячейке F10
— это у-пересечение
прямой линии (b
= 27920,1). Можно
составить линейную модель, описывающую
динамику товарооборота торгового
предприятия, которая принимает следующий
вид:
Y
= 27920,1 + 437,425x,
где
х = t
— порядковый номер месяца.
В
нашем примере коэффициент корреляции
(см. таблицу 3.12, ячейка Е12) r2
= 0,9179, что
указывает на высокое качество линейной
модели.
В
нашем примере Fкрит
находится по таблице F-распределения
на пересечении столбца 1 (так как в модели
только одна переменная х
— временной тренд) и строки 14 (см. ячейку
F13
таблицы 3.12). В приложении А находим для
распределения Фишера с (1;14) степенями
свободы, что при 5%-м уровне значимости
(доверительная вероятность 95 %) табличное
значение Fкp
= 4,6. Поскольку
F
= 156,567 > 4,6
(см. ячейку Е13 таблицы 3.12), то полученная
модель тренда полезна для использования
в прогнозировании.
Рассчитаем
значения t-статистики
для оценки параметров m
и b
построенной нами модели на основе данных
таблицы 3.12:
Табличное
значение tкрит
для уровня значимости 0,05 (доверительная
вероятность 0,95) с df
= 14 степенями свободы равно 2,145 (см.
приложение Б). Поскольку |tm|
> 2,145, |tf|
> 2,145, статистическая значимость
параметров построенной модели признается
весьма высокой.
Задание
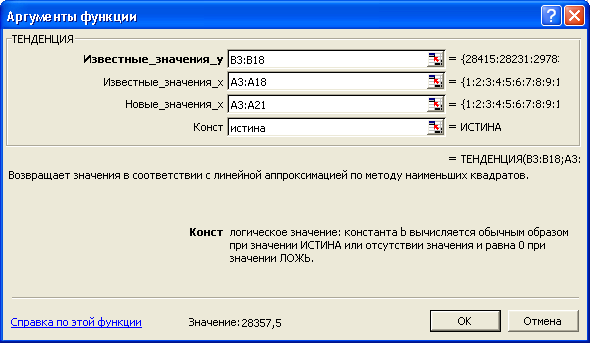
7. Использование функции ТЕНДЕНЦИЯ для
построения прогнозов
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ТЕНДЕНЦИЯ.
Выполнение:
Функция
ТЕНДЕНЦИЯ рассчитывает прогнозные
значения исследуемого показателя в
соответствии с линейным трендом. Она с
помощью метода наименьших квадратов
аппроксимирует прямой линией массивы
известных значений у
и известных
значений х,
а также определяет точки, лежащие на
этой линии, и прогнозирует значения
у
для вновь заданных значений х.
Но при этом ТЕНДЕНЦИЯ не приводит
математического описания и
статистических характеристик самой
модели тренда.
Вызвать
функцию ТЕНДЕНЦИЯ можно из окна диалога
Мастера
функций,
расположенного на панели Стандартная,
в категориях – Статистические.
ТЕНДЕНЦИЯ имеет четыре аргумента
(рисунок 3.12):
1)
Известные
значения у;
2)
Известные
значения х;
3)
Новые значения
х;
4)
Конст.
Первый,
второй и четвертый аргументы формируются
аналогично тому, как это происходит при
работе с функцией ЛИНЕЙН (соответственно
первым, вторым и третьим ее аргументом).
Третий
аргумент — это определяемые самим
пользователем значения х
(в модели тренда — времени t),
для которых ТЕНДЕНЦИЯ рассчитывает по
найденной модели соответствующие
значения у.
Так, при прогнозировании товарооборота
торгового предприятия с помощью функции
ТЕНДЕНЦИЯ на рабочем листе выделим
диапазон ячеек С3:С21, где ячейки С3:С18 —
для отражения значений каждой точки
базового интервала времени на линии
тренда (таблица 3.14), а ячейки С19:С21 — для
перспективной оценки товарооборота на
три ближайших месяца. Аргумент Новые
значения х
в этом случае будет задан ячейками
А3:А21, и формируется следующая формула
массива: =ТЕНДЕНЦИЯ(В3:В18;А3:А18;А3:А21).
По
окончании работы с окном диалога
ТЕНДЕНЦИЯ необходимо нажать на клавиатуре
кнопки Ctrl
+ Shift
+ Enter.
В выходном диапазоне (см. столбец С
таблицы 3.14) функция ТЕНДЕНЦИЯ
моментально отразит все рассчитанные
на основе линейной модели тренда значения
у,
соответствующие заданному аргументу
Новые значения
х (т.е. ячейкам
А3:А21). Из них значения, находящиеся в
ячейках С3:С18, будут относиться к базовому
временному интервалу, а в ячейках С19:С21
— содержать прогноз товарооборота на
17-й, 18-й и 19-й месяцы.
Рисунок 3.12 — Окно
диалога функции ТЕНДЕНЦИЯ
Таблица
3.14 — Расчет прогноза товарооборота с
помощью функции ТЕНДЕНЦИЯ
|
А |
В |
С |
|
|
1 |
|||
|
2 |
Порядковый |
Объем |
Тенденция |
|
3 |
1 |
28415 |
28358 |
|
4 |
2 |
28231 |
28795 |
|
5 |
3 |
29783 |
29232 |
|
6 |
4 |
30969 |
29670 |
|
7 |
5 |
30494 |
30107 |
|
8 |
6 |
29757 |
30545 |
|
9 |
7 |
30850 |
30982 |
|
10 |
8 |
31325 |
31419 |
|
11 |
9 |
31359 |
31857 |
|
12 |
10 |
31610 |
32294 |
|
13 |
11 |
32366 |
32732 |
|
14 |
12 |
33313 |
33169 |
|
15 |
13 |
33508 |
33607 |
|
16 |
14 |
33374 |
34044 |
|
17 |
15 |
34811 |
34481 |
|
18 |
16 |
36046 |
34919 |
|
19 |
17 |
35356 |
|
|
20 |
18 |
35794 |
|
|
21 |
19 |
36231 |
Задание
8. Использование функции ПРЕДСКАЗ для
построения прогнозов
Составить
прогноз товарооборота торгового
предприятия по данным таблицы 3.6 с
помощью функции ПРЕДСКАЗ.
Выполнение:
Функция
ПРЕДСКАЗ определяет лишь одну точку на
линии тренда и не может рассчитать
массив, который формирует эту линию.
Поэтому ее удобно использовать для
оперативного вычисления единичных
прогнозов. Функцию ПРЕДСКАЗ можно
вызвать в диалоговом окне Мастера
функций, в
категориях – Статистические,
она имеет только три аргумента (рисунок
3.13):
1)
X
— это точка данных (числовое значение),
для которой необходимо рассчитать
прогноз исследуемого показателя.
Так,
при прогнозировании товарооборота на
17-й,
18-й и 19-й месяцы
(таблица 3.15) в качестве аргумента X
определим ячейки А19:А21;
2)
Известные
значения у
(прогнозируемого показателя). В нашем
примере их можно задать в виде диапазона
ячеек В3:В18 (см. таблицу 3.15);
3)
Известные
значения х
(времени t).
Этот аргумент должен совпадать по
размерам с массивом Известные
значения у.
Этот аргумент в нашем примере охватывает
ячейки А3:А18.
Соответственно
обозначенным в окне диалога ПРЕДСКАЗ
аргументам формируется формула следующего
вида: =ПРЕДСКАЗ(А19:А21;В3:В18;А3:А18).
По
окончании работы с окном диалога ПРЕДСКАЗ
необходимо нажать на клавиатуре кнопки
Ctrl
+ Shift
+ Enter.
Рисунок 3.13 — Окно
диалога функции ПРЕДСКАЗ
Таблица
3.15 — Расчет прогноза товарооборота с
помощью функции ПРЕДСКАЗ
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.3
1
28415
4
2
28231
5
3
29783
6
4
30969
7
5
30494
8
6
29757
Продолжение таблицы
3.15
-
А
В
С
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.9
7
30850
10
8
31325
11
9
31359
12
10
31610
13
11
32366
14
12
33313
15
13
33508
16
14
33374
17
15
34811
18
16
36046
19
17
35356
ПРЕДСКАЗ
20
18
35794
21
19
36231
Задание
9. Анализ нелинейных процессов с помощью
функции ЛГРФПРИБЛ
Рассчитать
параметры модели тренда и дать ей
качественную оценку с помощью функции
ЛГРФПРИБЛ для базовых данных о динамике
товарооборота предприятия, приведенных
в таблице 3.6.
Выполнение:
Функция
ЛГРФПРИБЛ определяет параметры
экспоненциальной кривой, наилучшим
образом аппроксимирующей исходные
данные. Эта функция относится к категории
«Статистические»
и может быть вызвана с помощью окна
диалога Мастера
функций.
Функция
ЛГРФПРИБЛ имеет те же четыре аргумента,
что и функция ЛИНЕЙН и формирует
аналогичный массив результатов (рисунок
3.14). Поэтому она вводится как формула
для работы с массивами, т.е. требует:
во-первых, выделения диапазона ячеек,
в которых будет формироваться массив
результатов; во-вторых, после работы с
окном диалога ЛГРФПРИБЛ — нажатия
клавиш Ctrl
+ Shift
+ Enter.
Однако
следует учитывать, что дополнительная
статистика, которую отражает функция
ЛГРФПРИБЛ, основана на линейной модели
вида
In
у = х
ln
т + ln
b.
Поэтому
при оценке значений стандартных ошибок
параметров модели (СОт
и COb)
их необходимо сравнивать не с самими
значениями параметров, а с их натуральными
логарифмами — ln
m
и ln
b.
Последние можно рассчитать с помощью
функции LN
(категория «Математические»),
вызывая ее в окне диалога Мастера
функций.
С
этой целью на рабочем листе Excel
выделим диапазон ячеек D11:E15
для формирования выходного массива
(таблица 3.16). Работая с окном диалога
ЛГРФПРИБЛ, формируем следующую формулу
массива: =ЛГРФПРИБЛ(В3:В18;А3:А18;ИСТИНА;
ИСТИНА). Затем нажимаем клавиши Ctrl
+ Shift
+ Enter.
Рисунок 3.14 — Окно
диалога функции ЛГРФПРИБЛ
Таблица
3.16 — Расчет и оценка модели тренда с
помощью функции ЛГРФПРИБЛ
|
A |
B |
C |
D |
E |
|
|
1 |
|||||
|
2 |
Порядковый номер |
Объем |
|||
|
3 |
1 |
28415 |
|||
|
4 |
2 |
28231 |
|||
|
5 |
3 |
29783 |
|||
|
6 |
4 |
30969 |
|||
|
7 |
5 |
30494 |
|||
|
8 |
6 |
29757 |
|||
|
9 |
7 |
30850 |
|||
|
10 |
8 |
31325 |
|||
|
11 |
9 |
31359 |
Экспоненциальная оценка |
1,014 |
28080,897 |
|
12 |
10 |
31610 |
Статистика |
0,001 |
0,010 |
|
13 |
11 |
32366 |
0,922 |
0,020 |
|
|
14 |
12 |
33313 |
165,579 |
14 |
|
|
15 |
13 |
33508 |
0,065 |
0,005 |
|
|
16 |
14 |
33374 |
|||
|
17 |
15 |
34811 |
|||
|
28 |
16 |
36046 |
Вывод:
Приведенный в таблице 3.16 массив
результатов работы функции позволяет
построить следующую модель тренда, в
основе которой лежит уравнение
экспоненциальной кривой роста:
у
= 28080,897 · 1,01х,
где
х = t
— порядковый номер месяца.
Оценка
статистических характеристик приведенной
модели показывает, что качество ее
подгонки к фактическим значениям у
выше, чем модели, построенной с помощью
функции ЛИНЕЙН. Коэффициент r2
в данном случае имеет значение 0,922
(ячейка D13),
что несколько больше соответствующего
показателя в случае линейной модели,
равного 0,9179. В этой связи (и учитывая
однофакторный характер модели) можно
ожидать улучшение оценок F—
и t-статистики.
Следовательно, качество построенной
модели позволяет использовать ее
при составлении прогнозов развития
товарооборота на ближайшую перспективу.
Задание
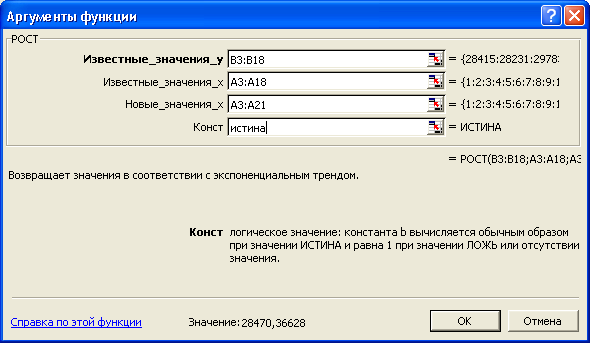
10. Составление нелинейных прогнозов с
помощью функции РОСТ
Учитывая
оценку статистических характеристик
функции ЛГРФПРИБЛ, рассчитать прогноз
товарооборота по торговому предприятию
с помощью функции РОСТ. При этом необходимо
получить теоретические значения
товарооборота (оцененные на основе
найденной модели у
= 28080,897·1,01х)
для базового диапазона времени (т.е.
16 прошедших месяцев), а также спрогнозировать
динамику товарооборота на ближайшие 3
месяца.
Выполнение:
Функция
РОСТ определяет точки, лежащие на
экспоненциальной кривой роста. Она
работает точно так же, как ее линейный
аналог ТЕНДЕНЦИЯ, и имеет те же четыре
аргумента (рисунок 3.15).
Подобно
функции ТЕНДЕНЦИЯ, РОСТ вводится как
формула массива и требует выделения
достаточного числа ячеек для формирования
выходного диапазона результатов.
Для
формирования выходного массива
результатов выделим на рабочем листе
Excel,
соответственно, ячейки С3:С21 (таблица
3.17). Затем вызовем функцию РОСТ из окна
диалога Мастера
функций. При
работе с диалоговым окном РОСТ формула
массива принимает вид:
=РОСТ(В3:В18;А3:А18;А3:А21). Последнее действие
— нажать клавиши Ctrl
+ Shift
+ + Enter.
Рисунок 3.15 — Окно
диалога функции РОСТ
Таблица
3.17 — Расчет прогноза товарооборота с
помощью функции РОСТ
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.РОСТ
3
1
28415
28470,4
4
2
28231
28865,2
5
3
29783
29265,6
6
4
30969
29671,5
7
5
30494
30083,0
8
6
29757
30500,3
9
7
30850
30923,3
10
8
31325
31352,2
11
9
31359
31787,0
12
10
31610
32227,9
13
11
32366
32674,9
14
12
33313
33128,1
15
13
33508
33587,5
16
14
33374
34053,4
17
15
34811
34525,7
18
16
36046
35004,5
19
17
35490,0
20
18
35982,3
21
19
36481,3
Задание
11. Прогнозирование с использованием
парной регрессии
Проанализировать
тесноту связи между товарооборотом
торгового предприятия и оборачиваемостью
товаров и найти уравнение парной
регрессии, которое наилучшим образом
опишет изучаемую зависимость. Исходные
данные представлены в таблице 3.18.
Таблица
3.18 — Исходные данные для поиска уравнения
связи переменных
-
А
В
С
1
2
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.Оборачиваемость
товаров, дни3
1
28415
43,5
4
2
28231
43,0
5
3
29783
43,0
6
4
30969
43,5
7
5
30494
43,0
8
6
29757
42,5
9
7
30850
43,0
10
8
31325
41,5
11
9
31359
42,0
12
10
31610
41,5
13
11
32366
40,5
Продолжение таблицы
3.18
-
А
В
С
Порядковый
номер месяцаОбъем
товарооборота, ден. ед.Оборачиваемость
товаров, дни14
12
33313
40,0
15
13
33508
40,0
16
14
33374
39,0
17
15
34811
39,5
18
16
36046
39,0
19
Выполнение:
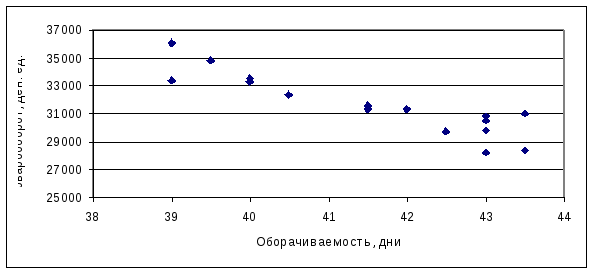
Чтобы
найти уравнение парной регрессии,
которое наилучшим образом опишет
изучаемую зависимость, обратимся к
графическому методу. С помощью Мастера
диаграмм построим
точечную диаграмму зависимости
товарооборота от оборачиваемости
товаров (см. рисунок 3.16).
Рисунок
3.16 — График зависимости товарооборота
от
товарооборачиваемости
товаров
После
того как диаграмма построена, необходимо
обратиться к команде Excel
«Добавить
линию тренда»
из контекстного меню панели Диаграмма.
Учитывая возможности Excel,
оценим качество аппроксимации базовых
данных каждым из пяти предлагаемых
окном диалога Линии
тренда типом
линий: для линейного уравнения
R2
= 0,8197; для уравнения логарифмической
кривой R2
= 0,8216; для уравнений полинома 4-й степени
R2
= 0,8287; для
уравнения степенной кривой R2
= 0,8155; для уравнения экспоненциальной
кривой R2
= 0,8142.
Полученные
результаты свидетельствуют, что наиболее
адекватно (судя по величине R2)
отражают зависимость товарооборота
от изменения товарооборачиваемости
кривые, построенные на основе уравнений
полиномов 4-й степени. На рисунке 3.17
приведена кривая роста, которую описывает
уравнение полинома 4-й степени. Рассчитанный
Excel
коэффициент R2
(0,8287) указывает на достаточно высокое
качество приближения базовых данных.
Рисунок
3.17 — Аппроксимация базовых данных
полиномиальной кривой роста
Проведем
оценку статистической значимости
параметров уравнения полинома 4-й
степени, построенного на основе
соответствующего массива базовых данных
(таблица 3.19, ячейки A2:F18)
с помощью функции ЛИНЕЙН. Для формирования
выходного массива значений параметров
уравнения и статистических характеристик
обозначим диапазон ячеек В20:F24.
Таблица
3.19 — Оценка статистической значимости
модели регрессии с помощью функции
ЛИНЕЙН (уравнение полинома 4-й степени)
|
А |
В |
С |
D |
E |
F |
|
|
1 |
||||||
|
2 |
Порядковый номер |
Объем товарооборота, |
Оборачиваемость |
х^2 |
х^3 |
х^4 |
|
3 |
1 |
28415 |
43,5 |
1892,3 |
82312,9 |
3580610,1 |
|
4 |
2 |
28231 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
5 |
3 |
29783 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
6 |
4 |
30969 |
43,5 |
1892,3 |
82312,9 |
3580610,1 |
|
7 |
5 |
30494 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
8 |
6 |
29757 |
42,5 |
1806,3 |
76765,6 |
3262539,1 |
|
9 |
7 |
30850 |
43 |
1849,0 |
79507,0 |
3418801,0 |
|
10 |
8 |
31325 |
41,5 |
1722,3 |
71473,4 |
2966145,1 |
|
11 |
9 |
31359 |
42 |
1764,0 |
74088,0 |
3111696,0 |
|
12 |
10 |
31610 |
41,5 |
1722,3 |
71473,4 |
2966145,1 |
|
13 |
11 |
32366 |
40,5 |
1640,3 |
66430,1 |
2690420,1 |
|
14 |
12 |
33313 |
40 |
1600,0 |
64000,0 |
2560000,0 |
|
15 |
13 |
33508 |
40 |
1600,0 |
64000,0 |
2560000,0 |
|
16 |
14 |
33374 |
39 |
1521,0 |
59319,0 |
2313441,0 |
|
17 |
15 |
34811 |
39,5 |
1560,3 |
61629,9 |
2434380,1 |
|
18 |
16 |
36046 |
39 |
1521,0 |
59319,0 |
2313441,0 |
|
19 |
17 (прогноз) |
36667 |
37,5 |
|||
|
20 |
2,269166117 |
-330,0698403 |
17765,93 |
-419248 |
3693351,7 |
|
|
21 |
Статистика |
100,6502388 |
16606,9862 |
1027052 |
28216610 |
290563825 |
|
22 |
0,828678371 |
1050,630858 |
#Н/Д |
#Н/Д |
#Н/Д |
|
|
23 |
13,30168019 |
11 |
#Н/Д |
#Н/Д |
#Н/Д |
|
|
24 |
58730919,23 |
12142077,21 |
#Н/Д |
#Н/Д |
#Н/Д |
При
определении в диалоговом окне ЛИНЕЙН
аргументов функции формируется
следующая формула массива:
=ЛИНЕЙН(В3:В18;С3:F18;ИСТИНА;ИСТИНА).
В
первой строке массива результатов,
отображенного функцией ЛИНЕЙН после
нажатия клавиш Ctrl
+ Shift
+ + Enter
(ячейки В20:F24
таблицы 3.19), находим уточненные в ходе
математических расчетов значения
параметров уравнения.
Вывод:
Модель связи товарооборота (у)
и оборачиваемости товаров (х),
построенная на основе уравнения полинома
4-й степени, имеет вид:
у
= 3693352 — 419248х + 17765,93х2
— 330,07х3
+ 2,269х4.
Заметьте,
что рассчитанный в массиве Статистика
коэффициент R2,
равный 0,8287 (ячейка В22), соответствует
значению R2,
приведенному на рисунке 3.17.
В
нашем примере (см. таблицу 3.19) значения
всех рассчитанных параметров уравнения
(ячейки В20:F20)
меньше по модулю значений их стандартных
ошибок (ячейки В21:F21).
Следовательно, надежность оценок
параметров регрессии не может быть
признана удовлетворительной и составленную
модель не следует применять для
прогнозирования исследуемого
показателя.
Используя
линии тренда Excel,
найдем уравнение другой кривой, для
которой значение R2
будет наибольшим. Таким образом,
наилучшее качество аппроксимации
исходных данных достигается в случае
уравнения логарифмической кривой
(рисунок 3.18).
Рисунок
3.18 — Аппроксимация базовых данных
логарифмической кривой роста
Статистическую
надежность сделанной оценки можно
проверить с помощью F-критерия,
расчетное значение которого в случае
парной регрессии определяют на основе
следующей формулы
.
Итак,
для уравнения парной регрессии с
коэффициентом R2,
равным 0,8216, F
=
64,5.
По
таблице F-распределения
(см. приложение А) находим, что при 5%-м
уровне значимости для распределения
Фишера с (1;14) степенями свободы Fкрит
= 4,60. Поскольку 64,5 > 4,60, можно сделать
вывод об адекватности и достаточной
точности модели. Следовательно, при
условии сохранения существовавшей
ранее взаимосвязи переменных на период
упреждения модель вида у
= -49619ln(х)
+ 216503 может
быть использована для прогнозирования.
Чтобы
составить прогноз объема товарооборота
на 17-й месяц, осталось определить значение
переменной х
(т.е. оборачиваемости товаров) для данного
месяца. Это значение может быть
получено (в зависимости от характера
показателя) на основе экстраполяционных
методов, методов экспертных оценок или
непосредственно задано составителем
прогноза. Так, будем полагать, что
рассматриваемое торговое предприятие
на 17-й месяц планирует проведение
определенных рекламных мероприятий
и выставки-продажи, что по оценкам
специалистов позволит ускорить
оборачиваемость товаров в среднем
на 1,5 дня. В этом случае товарооборачиваемость
по предприятию в прогнозируемом месяце
составит 37,5 дня.
Прогноз
объема товарооборота можно получить,
создав соответствующую модели формулу
в любой (предварительно выделенной)
ячейке рабочего листа. Выделим, к
примеру, ячейку В19 (см. таблицу 3.19) и
внесем в нее следующую формулу:
=-49619*ln(37,5)+216503.
После нажатия клавиши Enter
в ячейке В19 отразится прогноз объема
товарооборота на 17-й месяц, равный 36 667
ден. ед.
Задание
12. Расчет и оценка уравнения множественной
регрессии средствами Excel
Построить
модель множественной линейной
регрессии, которая позволит оценить
объем товарооборота на ближайшую
перспективу при заданных параметрах
независимых переменных: «оборачиваемость
товаров» и «удельный вес товаров с
высокими торговыми надбавками».
Исходные данные представлены в таблице
3.20.
Таблица
3.20 — Исходные данные
|
А |
В |
С |
D |
|
|
1 |
||||
|
2 |
Порядковый |
Объем товарооборота, |
Оборачиваемость |
Удельный вес |
|
3 |
1 |
28415 |
43,5 |
22,5 |
|
4 |
2 |
28231 |
43,0 |
18,0 |
|
5 |
3 |
29783 |
43,0 |
24,9 |
|
6 |
4 |
30969 |
43,5 |
24,4 |
|
7 |
5 |
30494 |
43,0 |
20,6 |
|
8 |
6 |
29757 |
42,5 |
19,0 |
|
9 |
7 |
30850 |
43,0 |
22,2 |
|
10 |
8 |
31325 |
41,5 |
21,6 |
|
11 |
9 |
31359 |
42,0 |
19,8 |
|
12 |
10 |
31610 |
41,5 |
19,7 |
|
13 |
11 |
32366 |
40,5 |
23,1 |
|
14 |
12 |
33313 |
40,0 |
23,9 |
|
15 |
13 |
33508 |
40,0 |
21,2 |
|
16 |
14 |
33374 |
39,0 |
20,4 |
|
17 |
15 |
34811 |
39,5 |
24,2 |
|
18 |
16 |
36046 |
39,0 |
26,5 |
Выполнение:
При
построении модели множественной
регрессии целесообразнее обратиться
к инструменту Excel
Регрессия,
который предлагает исчерпывающую
статистическую информацию о ее параметрах
и качестве. Порядок работы с инструментом
Регрессия
определяется соответствующим окном
диалога. Его можно вызвать через команду
Анализ данных
из контекстного меню панели Сервис.
Диалоговое окно Регрессия
предлагает пользователю определиться
с набором следующих параметров (рисунок
3.19):
1)
Входной
интервал У
— предлагает ввод ссылки на ячейки
рабочего листа, которые содержат диапазон
базовых данных зависимой переменной у
(исследуемого показателя). В нашем
примере Входной
интервал Y
– В2:В18;
2)
Входной
интервал X
— предполагает ввод ссылки на ячейки
рабочего листа, которые содержат диапазон
базовых данных независимых переменных
х1,
х2,
…, xk.
В нашем примере Входной
интервал Х
– С2:D18;
3)
Метки
— требует установления флажка, если
первая строка входного интервала
содержит заголовки (названия столбцов).
Если заголовки отсутствуют, то флажок
устанавливать не нужно — Excel
автоматически создаст соответствующие
названия для данных выходного диапазона.
В нашем примере – устанавливаем флажок;
4)
Уровень
надежности
— позволяет пользователю определить
необходимый уровень надежности оценки
выходного диапазона значений. По
умолчанию Excel
применяет уровень 95 %. Если его нужно
изменить, то для данного параметра
следует установить флажок и в специально
открывшееся поле ввести нужный
уровень надежности. В нашем — примере
флажок не устанавливаем;
5)
Константа-ноль
— требует установления флажка, если
для уравнения регрессии не нужно
рассчитывать параметр b
(свободный член). В этом случае Excel
принимает b,
равным нулю. В нашем примере – флажок
не устанавливаем;
6)
Выходной
диапазон —
предполагает ввод ссылки на верхнюю
левую ячейку выходного диапазона.
Выходной массив значений будет занимать
не менее семи столбцов и содержать три
основных раздела: 1. Регрессионная
статистика; 2. Дисперсионный анализ;
3. Параметры (коэффициенты) регрессии и
характеристики их статистической
значимости;
7)
Новый лист
— применяют, если результаты анализа
следует разместить на новом листе книги,
начиная с ячейки А1;

Новая книга
— используется, если результаты анализа
необходимо разместить на первом листе
специально открытой для этого новой
книги;
9)
Остатки
— требует установления флажка, если в
целях проведения углубленного
статистического анализа качества
модели в выходной диапазон, кроме трех
основных разделов, необходимо включить
значения отклонений фактических
данных исследуемого показателя от
соответствующих им точек регрессионной
прямой (У
фактическое — У
расчетное);
10)
Стандартизированные
остатки —
применяют с той же целью для включения
в выходной диапазон значений стандартных
остатков;
11)
График
остатков —
используется, если для статистического
анализа необходимо построить диаграммы
остатков для каждой независимой
переменной х;
12)
График подбора
— предполагает формирование на рабочем
листе диаграмм, позволяющих отследить
характер связи и степень разброса
наблюдаемых и предсказанных значений
исследуемого показателя у
с каждой независимой переменной х;
13)
График
нормальной вероятности
— требует установления флажка, если
пользователю необходимо получить
график нормального распределения
вероятности для исследуемого
показателя.
Рисунок
3.19 — Окно диалога Регрессия
Так,
в первом разделе выходного массива
«Регрессионная
статистика»
(см. ячейки А4:В8 таблицы 3.21) приведены
основные статистические характеристики
общего качества уравнения: коэффициент
множественной корреляции R,
коэффициент детерминации R2,
стандартная ошибка оценки. Значение
R2,
равное 0,892, свидетельствует о том, что
на основе полученного уравнения регрессии
можно объяснить 89,2 % вариации объема
товарооборота.
Статистические
характеристики второго раздела выходного
массива «Дисперсионный
анализ»
(ячейки A10:F14)
позволяют оценить меру разброса
(дисперсию) зависимой переменной у
и остаточной вариации (дисперсии)
отклонений вокруг линии регрессии.
Так, значение SSр
(ячейка С12) характеризует часть
дисперсии, объясненную регрессией, а
SSо
(ячейка С13) — часть дисперсии, не
объясненной регрессией из-за наличия
ошибок ε. При проведении регрессионного
анализа особый интерес представляет
изменение этих значений по мере
введения каждого регрессора. Качество
модели улучшится, если после введения
в нее нового фактора значение
объясненной части дисперсии возрастет,
а не объясненной — снизится.
В
ячейках D12:D13
отражены соответственно дисперсия
исходного ряда (МSp
= SSp
/ df,
где df
= k
— см. ячейку В12) и несмещенная дисперсия
остаточной компоненты (MS0
= SS0
/ df,
где df
= п — k
— 1 — см.
ячейку В13).
В
ячейке F12
второго раздела выходного массива
приведен уровень значимости для
оцененного F.
Значения
F-статистики
(53,72) выглядит вполне допустимым,
поскольку уровень значимости для нее
(5,2107)
остается гораздо ниже 5%-го предела,
принятого для табличных F-статистик.
Следовательно, есть основания ожидать,
что F-наблюдаемое
будет больше Fкрит.
Оценив
на основе первого и второго разделов
выходного массива общее качество модели
связи и убедившись в ее значимости,
можем перейти к третьему разделу (см.
ячейки A16:G19
таблицы 3.21), который содержит детальную
информацию о параметрах уравнения
регрессии. Приведенные в ячейках
В17:В19 значения параметров (коэффициентов)
уравнения позволяют придать формальный
вид модели, построенной с помощью
регрессионного анализа:
у
= 71650,26 – 1098,94х1
+
255,838х2,
где
х1
— оборачиваемость товаров, дни; х2
— удельный вес товаров с высокими
торговыми надбавками, %.
Оценить
значимость каждого параметра позволяют
значения t-статистики
(см. ячейки D17:D19).
Можно использовать приведенный в
выходном массиве уровень значимости
(см. ячейки Е17:Е19): если он не превышает
0,05 (т.е. 5%-го уровня), то рассчитанные
характеристики t-статистики
будут больше табличного значения.
Следовательно, статистическая
значимость рассчитанных параметров
уравнения весьма высока.
И,
наконец, наряду с точечными значениями
коэффициентов регрессии третий
раздел выходного массива позволяет
получить их интервальные оценки с
доверительной вероятностью 95 % (см.
ячейки F17:G19
таблицы 3.21):
58598,85
<
b
<
84701,68; -1370,81 <
m1
<
-827,08; 68,597 <
m2
<
443,079.
На
основании изложенного можно с 95%-й
уверенностью утверждать, что параметры
уравнения содержат информацию, значимую
для расчета исследуемого показателя.
Таблица
3.21 — Регрессионный анализ
|
А |
В |
С |
D |
E |
F |
G |
|
|
1 |
ВЫВОД |
||||||
|
2 |
|||||||
|
3 |
Регрессионная статистика |
||||||
|
4 |
Множественный |
0,94449 |
|||||
|
5 |
R-квадрат |
0,892061 |
|||||
|
6 |
Нормированный |
0,875455 |
|||||
|
7 |
Стандартная |
767,1098 |
|||||
|
8 |
Наблюдения |
16 |
|||||
|
9 |
|||||||
|
10 |
Дисперсионный |
||||||
|
11 |
df |
SS |
MS |
F |
Значимость |
||
|
12 |
Регрессия |
2 |
63223048,8 |
31611524,42 |
53,7193 |
5,2E-07 |
|
|
13 |
Остаток |
13 |
7649947,59 |
588457,5077 |
|||
|
14 |
Итого |
15 |
70872996,4 |
||||
|
15 |
|||||||
|
16 |
Коэффициенты |
Стандартная |
t-статистика |
P-Значение |
Нижние |
Верхние |
|
|
17 |
Y-пересечение |
71650,26 |
6041,29087 |
11,86009163 |
2,41E-08 |
58598,85 |
84701,68 |
|
18 |
Оборачиваемость |
-1098,94 |
125,841366 |
-8,732770177 |
8,46E-07 |
-1370,81 |
-827,08 |
|
19 |
Удельный |
255,8378 |
86,6708225 |
2,951832613 |
0,011232 |
68,59687 |
443,0787 |
Cтатистический анализ данных, моделирование и прогноз
Электронный процессор Excel позволяет строить математические модели
по
имеющимся табличным данным. Математическая модель дает возможность
прогнозировать состояние моделируемого объекта и выбирать на этой основе
оптимальное управление объектом. Для этих целей Excel содержит пакет
анализа данных, в который входят: регрессионный анализ, корреляция,
дисперсионный анализ и другие средства.
Регрессионный анализ
Регрессионный анализ позволяет получить функциональную зависимость
между некоторой случайной величиной Y и некоторыми влияющими на Y
величинами X. Такая зависимость получила название уравнения регрессии. Различают простую (парную) и множественную регрессию линейного и нелинейного типа.
Пример простой линейной регрессии:
y=m1x+b.
Пример множественной линейной регрессии:
|
y=m1x1+m2x2+… |
(1) |
Для оценки степени связи между величинами используется коэффициент
множественной корреляции R Пирсона (корреляционное отношение), который
может принимать значения от 0 до 1. R=0 если между величинами нет
никакой связи и R=1, если между величинами имеется функциональная
(детерминированная) связь. В большинстве случаев R принимает
промежуточные значения от 0 до 1. Величина
R2 называется коэффициентом детерминации.
Задачей построения регрессионной зависимости является нахождение вектора
коэффициентов M модели (1) при котором коэффициент R принимает максимальное значение.
Для оценки значимости R применяется F-критерий Фишера, вычисляемый по
формуле
где n — размер выборки (количество экспериментов); k — число
коэффициентов модели.
Если F превышает некоторое критическое значение для данных n и k и
принятой
доверительной вероятности, то величина R считается существенной. Таблицы
критических значений F приводятся в справочниках по математической
статистике.
Таким образом, значимость R определяется не только его величиной, но и
соотношением между количеством экспериментов и количеством коэффициентов
(параметров) модели. Действительно, корреляционное отношение для n=2
для простой линейной модели равно 1 (через 2 точки на плоскости можно
всегда провести единственную прямую). Однако, если экспериментальные
данные являются случайными величинами, доверять такому значению R
следует с большой осторожностью. Обычно для получения значимого R и
достоверной регрессии стремятся к тому, чтобы количество экспериментов
существенно превышало количество коэффициентов модели (n>>k).
Для построения линейной регрессионной модели необходимо:
1) подготовить список из n строк и m столбцов, содержащий
экспериментальные данные (столбец, содержащий выходную величину y должен
быть либо первым, либо последним в списке);
2) обратиться к меню Сервис/Анализ данных/Регрессия
Если пункт «Анализ данных» в меню «Сервис» отсутствует, то следует обратиться к пункту «Надстройки» того же меню и установить флажок «Пакет анализа».
3) в диалоговом окне «Регрессия» задать:
- входной интервал Y;
- входной интервал X;
- выходной интервал — верхняя левая ячейка интервала, в который будут
помещаться результаты вычислений (рекомендуется разместить на новом
рабочем листе);
4) нажать «Ok» и проанализировать результаты.
Пример использования множественной линейной регрессии
Предположим, что застройщик оценивает стоимость группы небольших офисных зданий в традиционном деловом районе.
Застройщик может использовать множественный регрессионный анализ для
оценки цены офисного здания в заданном районе на основе следующих
переменных.
y — оценочная цена здания под офис;
x1 — общая площадь в квадратных метрах;
x2 — количество офисов;
x3 — количество входов (0,5 входа означает вход только для доставки
корреспонденции);
x4 — время эксплуатации здания в годах.
В этом примере предполагается, что существует линейная зависимость между
каждой независимой переменной (x1, x2,
x3 и x4) и зависимой переменной (y), то есть ценой здания под офис в данном районе. Исходные данные показаны на рисунке.
Настройки для решения поставленной задачи показаны на рисунке окна
«Регрессия». Результаты расчетов размещены на отдельном листе в трех
таблицах
В итоге мы получили следующую математическую модель:
y = 52318 + 27,64*x1 + 12530*x2 + 2553*x3 —
234,24*x4.
Теперь застройщик может определить оценочную стоимость здания под
офис в том же районе. Если это здание имеет площадь 2500 квадратных
метров, три офиса, два входа и время эксплуатации — 25 лет, можно
оценить его стоимость, используя следующую формулу:
y = 27,64*2500 + 12530*3 + 2553*2 — 234,24*25 + 52318 = 158 261 у.е.
В регрессионном анализе наиболее важными результатами являются:
- коэффициенты при переменных и Y-пересечение, являющиеся искомыми
параметрами модели; - множественный R, характеризующий точность модели для имеющихся
исходных данных; - F-критерий Фишера (в рассмотренном примере он значительно превосходит критическое значение, равное 4,06);
- t-статистика – величины, характеризующие степень значимости отдельных
коэффициентов модели.
На t-статистике следует остановиться особо. Очень часто при
построении
регрессионной модели неизвестно, влияет тот или иной фактор x на y.
Включение в модель факторов, которые не влияют на выходную величину,
ухудшает качество модели.
Вычисление t-статистики помогает обнаружить такие факторы. Приближенную
оценку можно сделать так: если при n>>k величина t-статистики по
абсолютному значению существенно больше трех, соответствующий
коэффициент следует считать значимым, а фактор включить в модель, иначе
исключить из модели. Таким образом, можно предложить технологию
построения регрессионной модели, состоящую из двух этапов:
1) обработать пакетом «Регрессия» все имеющиеся данные, проанализировать
значения t-статистики;
2) удалить из таблицы исходных данных столбцы с теми факторами, для
которых коэффициенты незначимы и обработать пакетом «Регрессия» новую
таблицу.
Для примера рассмотрим переменную x4. В справочнике по математической
статистике t-критическое с (n-k-1)=6 степенями свободы и доверительной
вероятностью 0,95 равно 1,94. Поскольку абсолютная величина t, равная
17,7 больше, чем 1,94, срок эксплуатации — это важная переменная для
оценки стоимости здания под офис. Аналогичным образом можно
протестировать все другие переменные на статистическую значимость.
Ниже приводятся наблюдаемые t-значения для каждой из независимых
переменных:
| Общая площадь | 5,1 |
| Количество офисов | 31,3 |
| Количество входов | 4,8 |
| Срок эксплуатации | 17,7 |
Все эти значения имеют абсолютную величину большую, чем 1,94;
следовательно, все переменные, использованные в уравнении регрессии,
полезны для предсказания оценочной стоимости здания под офис в данном
районе.
 Контрольные вопросы
Контрольные вопросы
- Какие средства для построения математических моделей и прогнозирования состояния моделируемого объекта содержит
Excel? - Каково назначение регрессионного анализа?
- Что такое уравнение регрессии?
- Какие виды регрессии различают? приведите примеры?
- Что показывает коэффициент множественной корреляции Пирсона?
- В чем заключается задача построения регрессионной зависимости?
- Для чего применяется F-критерий Фишера? Как он вычисляется?
- Какими параметрами определяется значимость коэффициента Пирсона?
- Как построить линейную регрессионную модель в
Excel? - Что характеризует t-статистика?
- Какова технология построения регрессионной модели?
Статистический анализ в MS Excel. Дисперсионный анализ, регрессии, метод наименьших квадратов.
Двухфакторный дисперсионный анализ с повторениями в MS EXCEL
Пусть имеется случайная переменная Y, значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от 2-х факторов, значения которых мы можем контролировать, т.е. задавать с требуемой точностью. Покажем …
update Опубликовано: 26 января 2019
Однофакторный дисперсионный анализ (one-way ANOVA) в MS EXCEL
Пусть имеется случайная переменная Y , значения которой мы можем измерять. Исследователь предполагает, что эта переменная зависит от фактора, значения которого мы можем контролировать, т.е. задавать с требуемой точностью. Покажем …
update Опубликовано: 26 января 2019
Функция MS EXCEL ЛИНЕЙН()
Функция ЛИНЕЙН() специально создана для оценки параметров линейной регрессии, а также для вывода регрессионной статистики (коэффициента детерминации, стандартных ошибок, F -статистики и др.).
update Опубликовано: 26 января 2019
Двухфакторный дисперсионный анализ без повторений в MS EXCEL
Решим задачу о сравнении средних значений нескольких выборок с использованием дисперсионного анализа в случае двух факторов без повторений (Two Factor ANOVA without Replication). Подход используемый для решения данной задачи имеет …
update Опубликовано: 26 января 2019
update Опубликовано: 26 января 2019
МНК: Степенная зависимость в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью степенной функции.
update Опубликовано: 11 ноября 2018
МНК: Приближение полиномом в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).
update Опубликовано: 24 ноября 2018
Простая линейная регрессия в MS EXCEL
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но …
update Опубликовано: 26 января 2019
Множественная регрессия в MS EXCEL
Рассмотрим использование MS EXCEL для прогнозирования переменной Y на основании нескольких переменных Х, т.е. множественную регрессию.
update Опубликовано: 26 января 2019
update Опубликовано: 26 января 2019
МНК: Метод Наименьших Квадратов в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции y = a x + …
update Опубликовано: 11 ноября 2018
МНК: Экспоненциальная зависимость в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
update Опубликовано: 11 ноября 2018
МНК: Приближение тригонометрическим полиномом в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью тригонометрического полинома.
update Опубликовано: 24 ноября 2018
update Опубликовано: 26 января 2019
update Опубликовано: 26 января 2019
МНК: Логарифмическая зависимость в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью логарифмической функции.
update Опубликовано: 11 ноября 2018
МНК: Квадратичная зависимость в MS EXCEL
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью квадратичной функции y=ax 2 +bx+с .
update Опубликовано: 24 ноября 2018
Диаграмма рассеяния в MS EXCEL
Построим диаграмму рассеяния для различных видов взаимосвязей двух переменных. Сгенерируем различные варианты трендов: линейный, квадратичный и затухающий синусоидальный.
update Опубликовано: 25 ноября 2018