Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
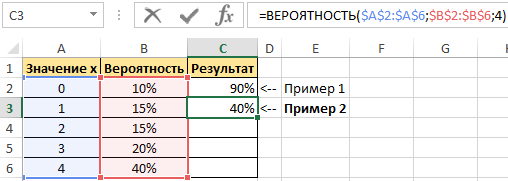
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
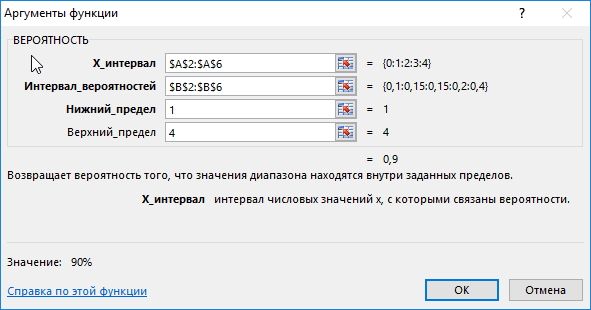
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
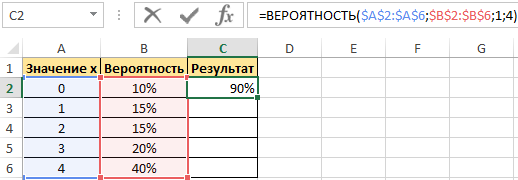
В результате выполненных вычислений получим:
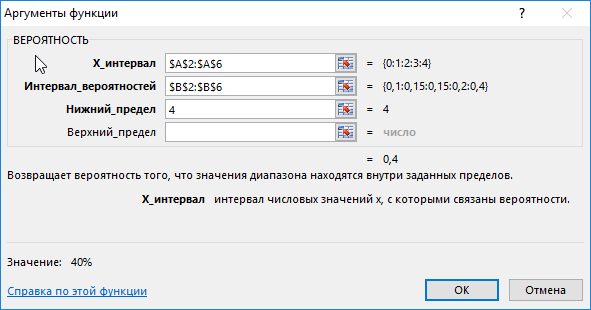
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
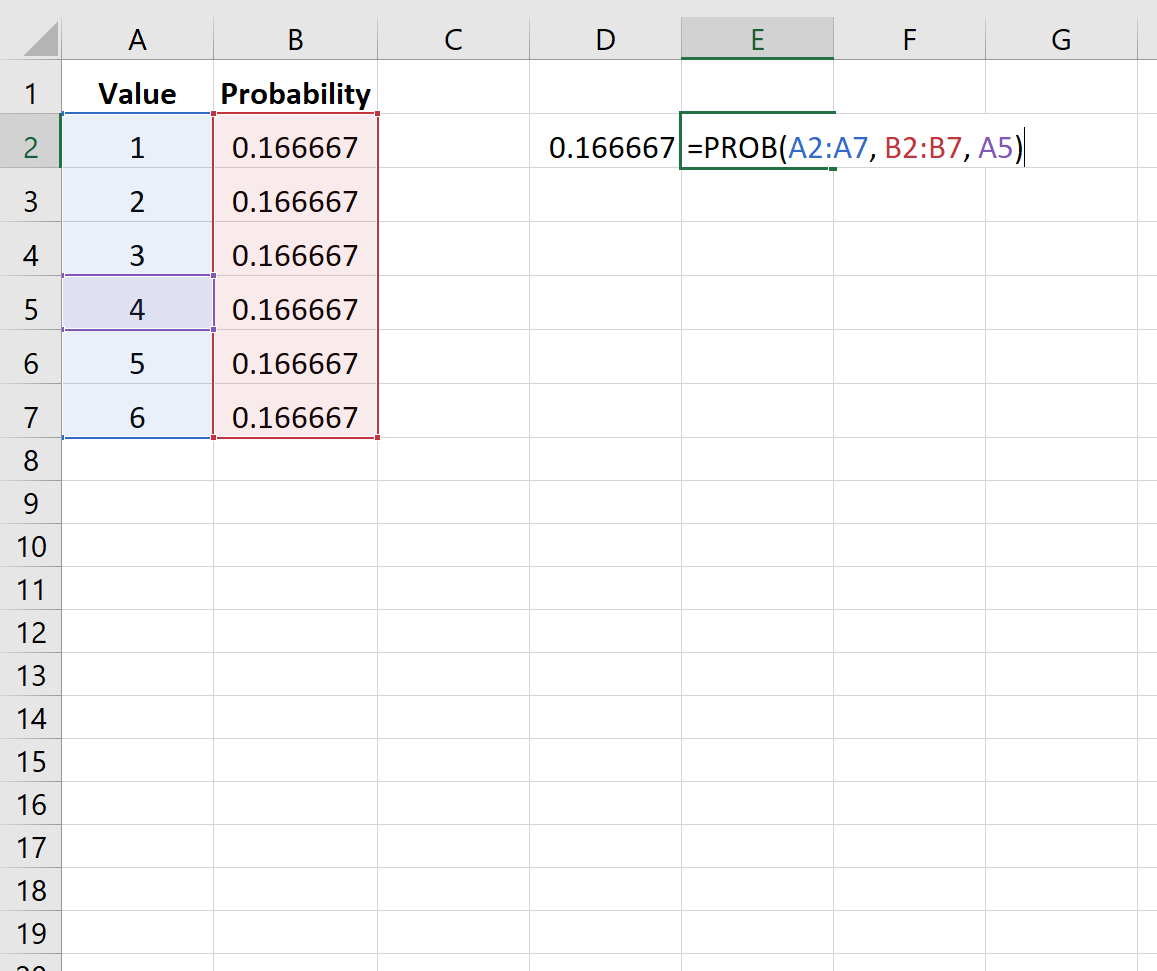
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
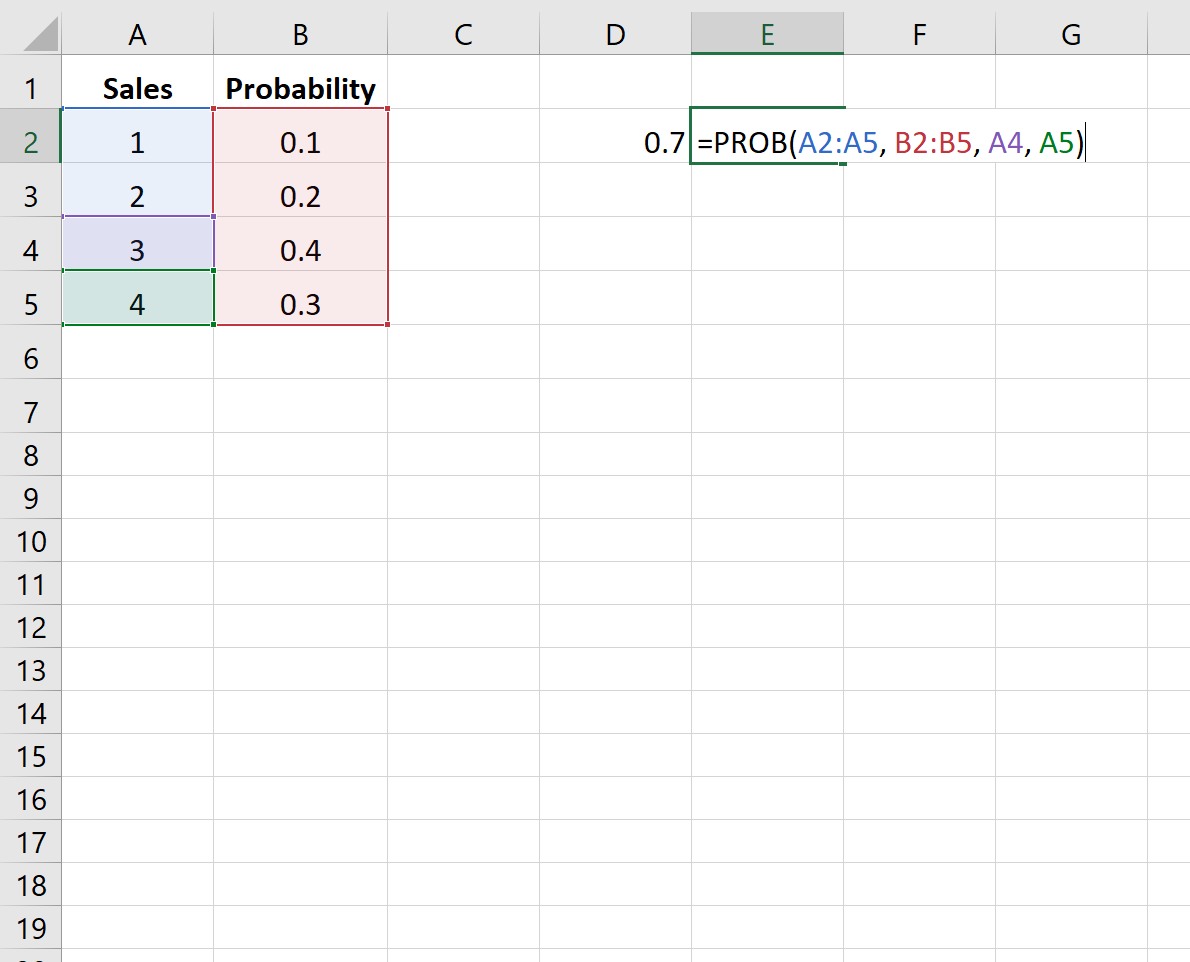
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Лучшее спасибо — порекомендовать эту страницу
Комбинаторика и вероятность
Ниже вы найдете основные формулы Excel, которые могут применяться при решении вероятностных задач и задач по комбинаторике.
| ЧИСЛКОМБ / COMBIN |
Возвращает количество сочетаний без повторений. |
| ФАКТР / FACT |
Вычисляет факториал числа. |
| СЛЧИС / RAND |
Выдает случайное число в интервале от 0 до 1 (равномерно распределенное). |
| СЛУЧМЕЖДУ / RANDBETVEEN |
Выдает случайное число в заданном интервале. |
| БИНОМРАСП / BINOMDIST |
Вычисляет отдельное значение биномиального распределения. |
| ГИПЕРГЕОМЕТ / HYRGEOMDIST |
Определяет гипергеометрическое распределение. |
| НОРМРАСП / NORMDIST |
Вычисляет значение нормальной функции распределения. |
| НОРМОБР / NORMINV |
Выдает обратное нормальное распределение. |
| НОРМСТРАСП / NORMSDIST |
Выдает стандартное нормальное интегральное распределение. |
| НОРМСТОБР / NORMSINV |
Выдает обратное значение стандартного нормального распределения. |
| ПЕРЕСТ / PERMUT |
Находит количество размещений без повторений |
| ВЕРОЯТНОСТЬ / PROB |
Определяет вероятность того, что значение из диапазона находится внутри заданных пределов. |
Подробнее: Формулы комбинаторики в Excel.
Подробно решим ваши задачи по теории вероятностей
Математическая статистика
При решении задач по математической статистике можно использовать те формулы, что перечислены выше, а также следующие (сгруппированы для удобства: обработка выборки, разные распределения, остальные формулы):
Обработка выборки: формулы Excel
| СРОТКЛ / AVEDEV |
Вычисляет среднее абсолютных значений отклонений точек данных от среднего. |
| СРЗНАЧ / AVERAGE |
Вычисляет среднее арифметическое аргументов. |
| СРГЕОМ / GEOMEAN |
Вычисляет среднее геометрическое. |
| СРГАРМ / HARMEAN |
Вычисляет среднее гармоническое. |
| ЭКСЦЕСС / KURT |
Определяет эксцесс множества данных. |
| МЕДИАНА / MEDIAN |
Находит медиану заданных чисел. |
| МОДА / MODE |
Определяет значение моды множества данных. |
| КВАРТИЛЬ / QUARTILE |
Определяет квартиль множества данных. |
| СКОС / SKEW |
Определяет асимметрию распределения. |
| СТАНДОТКЛОН / STDEV |
Оценивает стандартное отклонение по выборке. |
| ДИСП / VAR |
Оценивает дисперсию по выборке. |
Законы распределений: формулы Excel
| БЕТАРАСП / BETADIST |
Определяет интегральную функцию плотности бета-вероятности. |
| БЕТАОБР / BETAINV |
Определяет обратную функцию к интегральной функции плотности бета-вероятности. |
| ХИ2РАСП / CHIDIST |
Вычисляет одностороннюю вероятность распределения хи-квадрат. |
| ХИ2ОБР / CHIINV |
Вычисляет обратное значение односторонней вероятности распределения хи-квадрат. |
| ЭКСПРАСП / EXPONDIST |
Находит экспоненциальное распределение. |
| FРАСП / FDIST |
Находит F-распределение вероятности. |
| FРАСПОБР / FINV |
Определяет обратное значение для F-распределения вероятности. |
| ФИШЕР / FISHER |
Находит преобразование Фишера. |
| ФИШЕРОБР / FISHERINV |
Находит обратное преобразование Фишера. |
| ГАММАРАСП / GAMMADIST |
Находит гамма-распределение. |
| ГАММАОБР / GAMMAINV |
Находит обратное гамма-распределение. |
| ПУАССОН / POISSON |
Выдает распределение Пуассона. |
| СТЬЮДРАСП / TDIST |
Выдает t-распределение Стьюдента. |
| СТЬЮДРАСПОБР / TINV |
Выдает обратное t-распределение Стьюдента. |
| ВЕЙБУЛЛ / WEIBULL |
Выдает распределение Вейбулла. |
Другое (корреляция, регрессия и т.п.)
| ДОВЕРИТ / CONFIDENCE |
Определяет доверительный интервал для среднего значения по генеральной совокупности. |
| КОРРЕЛ / CORREL |
Находит коэффициент корреляции между двумя множествами данных. |
| СЧЁТ / COUNT |
Подсчитывает количество чисел в списке аргументов. |
| СЧЁТЕСЛИ / COUNTIF |
Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона. |
| КОВАР / COVAR |
Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек. |
| ПРЕДСКАЗ / FORECAST |
Вычисляет значение линейного тренда. |
| ЛИНЕЙН / LINEST |
Находит параметры линейного тренда. |
| ПИРСОН / PEARSON |
Определяет коэффициент корреляции Пирсона. |
Справочный файл по формулам Excel
Нужна шпаргалка по функциям Excel под рукой? Скачивайте файл: Математические и статистические формулы Excel
Полезные ссылки
|
|
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике:
Распределения вероятностей в MS EXCEL. Нормальное распределение, Биномиальное распределение, распределение Стьюдента, Вейбулла, Фишера и др. Оценка параметров распределения, вычисление математического ожидания и дисперсии. Функции MS EXCEL: НОРМ.РАСП(), СТЬЮДЕНТ.РАСП(), ХИ2.РАСП() и др. Рассмотрены ВСЕ распределения, имеющиеся в MS EXCEL 2010.
Взаимосвязь некоторых распределений в MS EXCEL
Рассмотрим взаимосвязь Биномиального распределения, распределения Пуассона, Нормального распределения и Гипергеометрического распределения. Определим условия, когда возможна аппроксимация одного распределения другим, приведем примеры и графики.
update Опубликовано: 06 ноября 2016
Функция распределения и плотность вероятности в MS EXCEL
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта <noindex> www.excel2.ru </noindex> . Рассмотрены примеры вычисления Функции распределения и Плотности …
update Опубликовано: 13 октября 2016
Нормальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Нормальное распределение. С помощью функции MS EXCEL НОРМ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения …
update Опубликовано: 23 октября 2016
Равномерное дискретное распределение в MS EXCEL
Рассмотрим Равномерное дискретное распределение, построим график функции распределения, вычислим среднее значение и дисперсию. Сгенерируем случайные значения (выборку) с помощью функции MS EXCEL СЛУЧМЕЖДУ() . На основании выборки оценим среднее и …
update Опубликовано: 27 октября 2016
Гипергеометрическое распределение. Дискретные распределения в MS EXCEL
Рассмотрим Гипергеометрическое распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГИПЕРГЕОМ.РАСП() построим графики функции распределения и плотности вероятности. Приведем пример аппроксимации гипергеометрического распределения биномиальным.
update Опубликовано: 07 ноября 2016
Биномиальное распределение. Дискретные распределения в MS EXCEL
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БИНОМ.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения …
update Опубликовано: 29 октября 2016
Распределения случайной величины в MS EXCEL
В статье приведен перечень распределений вероятности, имеющихся в MS EXCEL 2010 и в более ранних версиях. Даны ссылки на статьи с описанием соответствующих функций MS EXCEL.
update Опубликовано: 23 октября 2016
Распределение Пуассона. Дискретные распределения в MS EXCEL
Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ПУАССОН.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и …
update Опубликовано: 06 ноября 2016
Равномерное непрерывное распределение в MS EXCEL
Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
update Опубликовано: 08 ноября 2016
Логнормальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Логнормальное распределение. С помощью функции MS EXCEL ЛОГНОРМ .РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по логнормальному закону, произведем оценку параметров распределения, среднего …
update Опубликовано: 08 ноября 2016
Экспоненциальное распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра …
update Опубликовано: 08 ноября 2016
Гамма распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Гамма распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ГАММА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров …
update Опубликовано: 09 ноября 2016
Распределение Вейбулла. Непрерывные распределения в MS EXCEL
Рассмотрим распределение Вейбулла, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ВЕЙБУЛЛ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров …
update Опубликовано: 09 ноября 2016
Бета распределение. Непрерывные распределения в MS EXCEL
Рассмотрим Бета-распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БЕТА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.
update Опубликовано: 10 ноября 2016
Случайная выборка из генеральной совокупности в MS EXCEL
Инструмент Пакета анализа MS EXCEL «Выборка» извлекает случайную выборку из входного диапазона, рассматривая его как генеральную совокупность. Также случайную выборку можно извлечь с помощью формул.
update Опубликовано: 14 ноября 2016
© Copyright 2013 — 2023 Excel2.ru. All Rights Reserved
Содержание
- Формула Бернулли в Excel
- Схема независимых испытаний
- Формула Бернулли в Эксель
- Примеры решений задач
- Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
- Примеры использования функции вероятность для расчетов в Excel
- Вычисление процента вероятности события в Excel
- Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
- Решение задач на вычисление вероятности в Excel
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
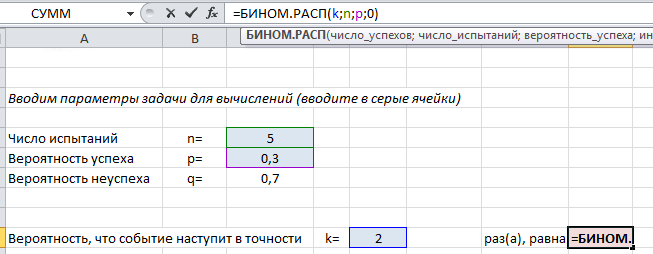
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
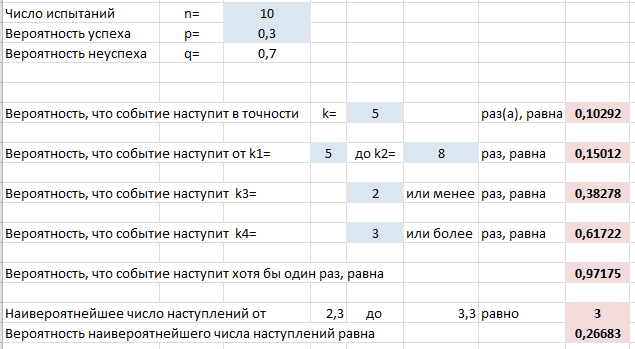
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Источник
Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Источник
Решение задач на вычисление вероятности в Excel
Пример 4. В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции = ГИПЕРГЕОМЕТ (1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: 
Для нахождения наиболее вероятного числа успехов k 0 по заданным n и р можно воспользоваться неравенствами np – q £ k 0£ np + p или правилом: если число np + p не целое, то k 0 равно целой части этого числа.
В случае, если n велико, р мало, а 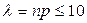

Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1- р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна 
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение. Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р 400(5)» 
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


Имеются таблицы, в которых помещены значения функции 
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 

Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 


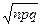

Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. Воспользуемся интегральной формулой Лапласа: n = 400; k 1 = 70; k 2 = 100; р = 0,2; q = 0,8; 

Для вычисления в Excel используем формулу нормального распределения = НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
Источник