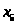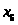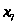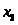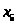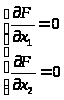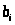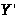Федеральное
агентство связи
Федеральное
государственное бюджетное образовательное
учреждение
высшего образования
Поволжский
государственный университет
телекоммуникаций
и информатики
Кафедра
Информационных систем и технологий
Лабораторная
работа №3
По
дисциплине «Теория принятия решений»
«Моделирование,
решение и анализ задач линейного
программирования»
Выполнили:
студенты группы ИСТ-74У
Гусева
Полина и Смолева Вера
Руководитель
:
__________________
Захарова
О.И.
Самара
2018
Тема:
Моделирование, решение и анализ задач
линейного программирования (ЛП).
Цель:
Изучить возможности надстройки Поиск
решения
пакета MS Excel
для решения однокритериальных задач
теории принятия решений.
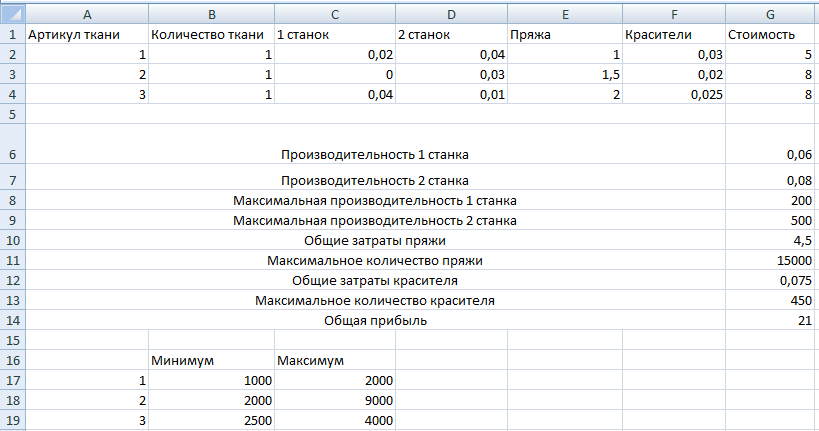
Задача
5
На ткацкой
фабрике для изготовления трёх артикулов
ткани используются станки двух типов,
пряжа и красители. В таблице указаны
производительность станка каждого
типа, нормы расхода пряжи и красителей,
цена 1 метра ткани данного артикула, а
также общий фонд рабочего времени
станков каждого типа, имеющихся в
распоряжении фабрики, фонды пряжи и
красителей и ограничения на возможный
выпуск тканей данного артикула.
Таблица 5
-
Ресурсы
Нормы затрат на
1 м ткани артикулаОбщее количество
ресурсов1
2
3
Производительность
станков (станко-ч):I
типаII
типаПряжа
(кг)Красители
(кг)Цена
1м ткани (руб.)Выпуск
ткани (м):Минимальный
Максимальный
0,02
0,04
1,0
0,03
5
1000
2000
—
0,03
1,5
0,02
8
2000
9000
0,04
0,01
2,0
0,025
8
2500
4000
200
500
15000
450
—
—
—
Составить
такой план изготовления тканей, согласно
которому будет произведено возможное
количество тканей данного артикула, а
общая стоимость всех тканей максимальна.
Дано:
x1
x2 x3
– артикул ткани
5x1+
8x2+ 8x3max
0.02x1+
0.04x3200
0.04x1+
0.03x2+0.01x3500
x1+
1.5x2+2x315000
0.03x1+
0.02x2+0.025x3450
1000≤x1≤2000
2000≤x2≤9000
2500≤x3≤4000

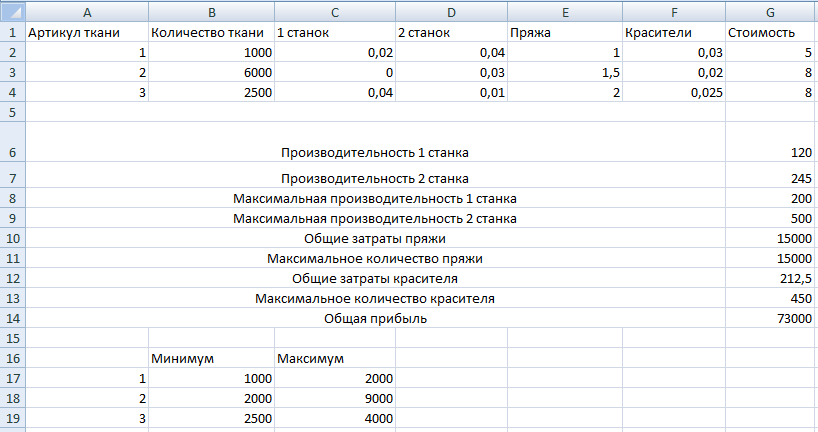
Задача
11
При
производстве четырёх видов кабеля
выполняется пять групп технологических
операций. Нормы затрат на 1 км кабеля
данного вида на каждой из групп операции,
прибыль
от
реализации 1 км каждого вида кабеля, а
также общий фонд рабочего времени, в
течение которого могут выполняться эти
операции, указаны в таблице.
Таблица 11
-
Технологическая
операцияНормы затрат
времени (ч) на обработку 1 км кабеля
видаОбщий фонд
рабочего времени (ч)1
2
3
4
Волочение
1,2
1,8
1,6
2,4
7200
Наложение
изоляции1,0
0,4
0,8
0,7
5600
Скручивание
элементов в кабель6,4
5,6
6,0
8,0
11176
Освинцевание
3,0
—
1,8
2,4
3600
Испытание и
контроль2,1
1,5
0,8
3,0
4200
Прибыль от
реализации 1 км кабеля1,2
0,8
1,0
1,3
—
Определить
такой план выпуска кабеля, при котором
общая прибыль от реализации изготовляемой
продукции является максимальной.
Дано:
x1
x2 x3
x4– артикул ткани
1.2x1+0.
8x2+
x3+
1.3x4max
1.2x1+1.
8x2+1.6
x3+
2.4x47200
x1+0.4x2+0.8
x3+
0.7x45600
6.4x1+5.6x2+6
x3+
8x411176
3x1+1.8x3+
2.4x43600
2.1x1+1.5x2+0.8x3+
3x411176
Вывод:
Изучены средства принятия решения
Microsoft Excel,
с помощью решения задачи, данной каждому
студенту по варианту.
Средство
Поиск решения может генерировать три
вида отчетов:
отчет по результатам, отчет по устойчивости
и отчет по пределам. Поиск решения
создает только для линейных моделей.
Для целочисленных моделей недоступны
отчеты по устойчивости и по пределам,
а для нелинейных моделей отчет по
устойчивости имеет другой вид.
Отчет
по результатам полезен для анализа
чувствительности только тем, что там
явно указано, какие ограничения связанные
и какие несвязанные. Эти данные приведены
в отчете в таблице Ограничения в столбце
Статус. В столбце Разница той же таблицы
показаны значения разностей между
левыми и правыми частями ограничений.
Если
статус «связанное», тогда данное
ограничение влияет на полученный план,
если «не связан» — значит не влияет. В
нашем случае ресурс 1 и 4 имеют статус
«не связан» — это значит, что эти ресурсы
не ограничивают возможности в производстве,
что не скажешь про ресурс 2 и 3, которые
использованы полностью;
Разница
между имеющемся в наличие количеством
ресурсов и использованных при полученном
плане.
1
задача

2
задача
Отчет
по устойчивости. В таблице Изменяемые
ячейки этого отчета приведена информация
о значениях изменяемых ячеек:
♦
адреса
изменяемых ячеек;
♦ их
имена (созданные заранее или составленные
из заголовков строк и столбцов, на
пересечении которых находятся изменяемые
ячейки); если имен нет, то это поле
остается пустым;
♦
значения
переменных в этих ячейках, найденные
средством Поиск решения;
♦
нормированная
стоимость — это значение равно нулю,
если значение соответствующей переменной
находится в границах своего возможного
изменения, но не достигает этих границ
(учитываются границы, которые задаются
явно в виде неравенств типа x ³ 0 и/или х
£ 100). Если переменная равна значению
одной из своих явно заданных границ
(например, равна нулю при заданном
условии неотрицательности), то значение
нормированной стоимости показывает,
насколько изменится значение целевой
функции, если значение этой переменной
увеличится на единицу1;
В
таблице Ограничения приведена информация
об ограничениях:
♦
адреса
ячеек, на значения которых наложены
ограничения;
♦ их
имена (созданные заранее или составленные
из заголовков строк и столбцов, на
пересечении которых находятся изменяемые
ячейки); если имен нет, то это поле
остается пустым;
♦
значения
в этих ячейках, найденные средством
Поиск решения;
♦
теневая
цена (Множитель Лагранжа) показывает,
насколько изменится значение целевой
функции, если на единицу изменится
значение правой части данного ограничения;
теневая цена отлична от нуля только
тогда, когда данное ограничение в
оптимальном решении является связанным
(и решение не вырождено);
1
задача
2
задача
В
отчете по пределам показано, в каких
пределах с учетом всех ограничений
могут изменяться переменные (значения
в столбцах Верхний предел и Нижний
предел) и какие при этом значения будет
принимать целевая функция (значения в
столбцах Целевой результат). Отметим,
что если на значения переменной не
налагаются явные ограничения, задающие
ее верхнюю (или нижнюю) границу, то в
столбцах Верхний предел и Целевой
результат (или Нижний предел и Целевой
результат) для этой переменной будут
стоять значения ошибки #Н/Д.
1
задача
2
задача
Соседние файлы в предмете Теория Принятия Решений
- #
- #
- #
03.08.202122.24 Кб743лб.xlsx
- #
03.08.2021198.11 Кб265.docx
- #
03.08.2021294.39 Кб226.docx
- #
- #
03.08.202113.04 Кб52Книга1.xlsx
Содержание
- Задача 12
- Лабораторная работа №1 пакет ms excel
- Что будем делать с полученным материалом:
- Все темы данного раздела:
- «Линейное программирование». Линейное программирование
- 3 лабораторка
Задача 12
Задача 12 — раздел Информатика, Лабораторная работа №1 пакет ms excel При Производстве Четырёх Видов Кабеля Выполняется Пять Групп Технологических .
При производстве четырёх видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км кабеля данного вида на каждой из групп операции, прибыль от реализации 1 км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
| Технологическая операция | Нормы затрат времени (ч) на обработку 1 км кабеля вида | Общий фонд рабочего времени (ч) | |||
| Волочение | 1,2 | 1,8 | 1,6 | 2,4 | |
| Наложение изоляции | 1,0 | 0,4 | 0,8 | 0,7 | |
| Скручивание элементов в кабель | 6,4 | 5,6 | 6,0 | 8,0 | |
| Освинцевание | 3,0 | — | 1,8 | 2,4 | |
| Испытание и контроль | 2,1 | 1,5 | 0,8 | 3,0 | |
| Прибыль от реализации 1 км кабеля | 1,2 | 0,8 | 1,0 | 1,3 | — |
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной. Кабель какого вида производить выгоднее всего?
Эта тема принадлежит разделу:
Лабораторная работа №1 пакет ms excel
Процесс принятия управленческого решения можно представить как.. i анализ ситуации и формализация исходной проблемы на этом этапе надо просто четко сформулировать проблему понять и..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача 12
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Лабораторная работа №1
Тема: Решение задач линейного программирования и анализ чувствительности с помощью MS Excel. Цель: Изучить возможности надстройки Поиск решения пакета MS
Задача 1
На швейной фабрике для изготовления четырёх видов изделий может быть использована ткань трёх артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней так же
Задача 2
Предприятие выпускает четыре вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов
Задача 3
Для перевозок груза на трёх линиях могут быть использованы суда трёх типов. Производительность судов при использовании их на различных линиях характеризуются данными, приведёнными в таблице. В ней
Задача 4
Компания «Bermuda Paint» специализируется на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства едини
Задача 5
Найти решение, состоящее в определении плана изготовления изделий A, B и C, обеспечивающего максимальный их выпуск, в стоимости выраженной с учётом ограничений на возможное использование сырья трёх
Задача 6
Полиграфическая компания выпускает рекламные издания LinksLetter и Ragged Edge, которые покупатели могут брать в местных магазинах и ресторанах Компания получает доход, продавая место для размещени
Задача 7
Завод может производить пять различных продуктов в произвольном соотношении. В выпуске каждого продукта принимают участие три станка, как показано в таблице. Все цифры даны в минутах на фунт продук
Задача 8
На ткацкой фабрике для изготовления трёх артикулов ткани используются станки двух типов, пряжа и красители. В таблице указаны производительность станка каждого типа, нормы расхода пряжи и красителе
Задача 9
Машиностроительное предприятие для изготовления четырёх видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. К
Задача 10
Для поддержания нормальной жизнедеятельности человеку необходимо потреблять не менее 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в
Задача 11
Для перевозок трёх видов продукции предприятие использует два типа технологического оборудования и два вида сырья. Нормы затрат сырья и времени на изготовление одного изделия каждого вида приведены
Задача 13
На мебельной фабрике изготовляется пять видов продукции: столы, шкафы, диваны-кровати, кресла-кровати и тахты. Нормы затрат труда, а также древесины и ткани на производство единицы продукции данног
Задача 14
Из четырех видов сырья необходимо составить смесь, в состав которой должно входить не менее 26 ед. химического вещества A, 30 ед. – вещества B и 24 ед. – вещества C. Количество единиц химического в
Источник
«Линейное программирование». Линейное программирование
| Название | Линейное программирование |
| Анкор | «Линейное программирование |
| Дата | 17.06.2020 |
| Размер | 178.66 Kb. |
| Формат файла |  |
| Имя файла | otchet_lr_8.docx |
| Тип | Лабораторная работа #130879 |
| Подборка по базе: Тест — Программирование.docx, 1с программирование.docx, линейное программирование.pptx, Access. Программирование на VBA. Часть 1.doc, Романов Д.В. Программирование_ИК.docx, ОП. 08 Компьютерное программирование (1).doc, Контрольная программирование.docx, Численные методы и программирование.doc, Суммативная работа за раздел Алгоритмизация и программирование.d, «Численные методы и программирование».doc
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА» Факультет «Информационных систем и технологий» Кафедра «Автоматизации предприятий связи»
ЛАБОРАТОРНАЯ РАБОТА № 7 Гибкие производственные системы |
Выполнил студент группы ИСТ-741: | ||||
| Соколко С. В. | |||||
| Фамилия И.О. | |||||
| Руководитель | доцент | ||||
| оценка | уч. степень., уч. звание | ||||
| Пиликина Е.А. | |||||
| дата, подпись | Фамилия И.О. |
Санкт-Петербург
- г.
Цель работы: освоить способы нахождения максимума линейной функции при заданной системе ограничений в среде MS Excel. Освоить применение надстройки «Поиск решения» для подбора оптимальных параметров.
При производстве четырех видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км кабеля данного вида для каждой из групп операций, прибыль от реализации 1 км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, приведенные далее.
Таблица 1 – Исходные данные
Для поиска решений воспользуемся алгоритмом решения оптимизационных задач с помощью инструментария MS Excel.
Заполним исходную таблицу (рисунок 1)
Рисунок 1 – Исходные данные и результаты расчета
Окно со значениями, задаваемыми при поиске решений представлено на рисунке 2.
При расчете прибыли использовалась формула =СУММПРОИЗВ($B$20:$E$20;B26:E26) (в ячейках F по вертикали, выделенных желтым).
Рисунок 2 – Параметры поиска решений
После выполнения поиска оптимальных решений, Excel позволяет сформировать в автоматическом режиме отчеты о результатах и об устойчивости. Далее приводится отчет о результатах.
Рисунок 3 – Отчет о результатах
Отчет об устойчивости приведен на рисунке 4.
Рисунок 4 – Отчет об устойчивости
Заключение: Во время поиска оптимального решения для заданной системы уравнений методами линейного программирования, были получены следующие результаты.
Источник
3 лабораторка
Федеральное агентство связи
Федеральное государственное бюджетное образовательное
учреждение высшего образования
Поволжский государственный университет
телекоммуникаций и информатики
Кафедра Информационных систем и технологий
Лабораторная работа №3
По дисциплине «Теория принятия решений»
«Моделирование, решение и анализ задач линейного программирования»
Выполнили: студенты группы ИСТ-74У
Гусева Полина и Смолева Вера
__________________ Захарова О.И.
Тема: Моделирование, решение и анализ задач линейного программирования (ЛП).
Цель: Изучить возможности надстройки Поиск решения пакета MS Excel для решения однокритериальных задач теории принятия решений.
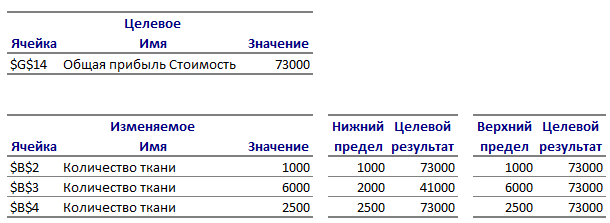
На ткацкой фабрике для изготовления трёх артикулов ткани используются станки двух типов, пряжа и красители. В таблице указаны производительность станка каждого типа, нормы расхода пряжи и красителей, цена 1 метра ткани данного артикула, а также общий фонд рабочего времени станков каждого типа, имеющихся в распоряжении фабрики, фонды пряжи и красителей и ограничения на возможный выпуск тканей данного артикула.
Нормы затрат на 1 м ткани артикула
Общее количество ресурсов
Производительность станков (станко-ч):
Цена 1м ткани (руб.)
Составить такой план изготовления тканей, согласно которому будет произведено возможное количество тканей данного артикула, а общая стоимость всех тканей максимальна.
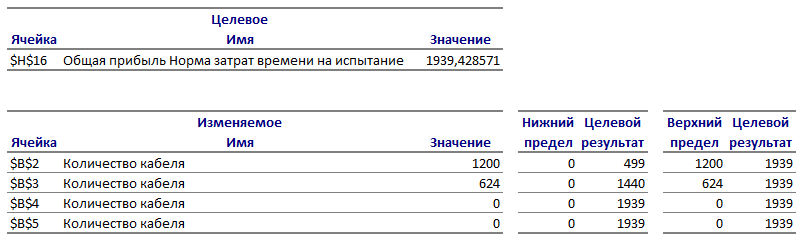
При производстве четырёх видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км кабеля данного вида на каждой из групп операции, прибыль
от реализации 1 км каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
Нормы затрат времени (ч) на обработку 1 км кабеля вида
Общий фонд рабочего времени (ч)
Скручивание элементов в кабель
Испытание и контроль
Прибыль от реализации 1 км кабеля
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной.
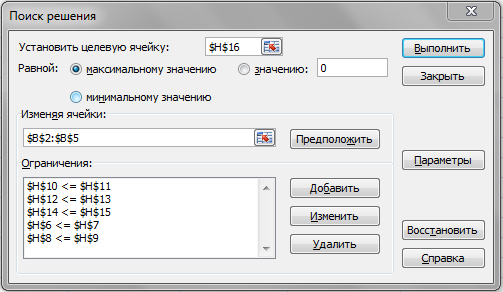
Вывод: Изучены средства принятия решения Microsoft Excel, с помощью решения задачи, данной каждому студенту по варианту.
Средство Поиск решения может генерировать три вида отчетов: отчет по результатам, отчет по устойчивости и отчет по пределам. Поиск решения создает только для линейных моделей. Для целочисленных моделей недоступны отчеты по устойчивости и по пределам, а для нелинейных моделей отчет по устойчивости имеет другой вид.
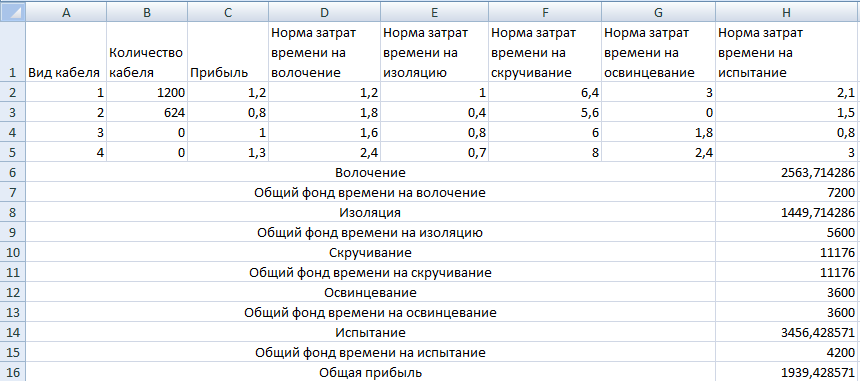
Отчет по результатам полезен для анализа чувствительности только тем, что там явно указано, какие ограничения связанные и какие несвязанные. Эти данные приведены в отчете в таблице Ограничения в столбце Статус. В столбце Разница той же таблицы показаны значения разностей между левыми и правыми частями ограничений.
Если статус «связанное», тогда данное ограничение влияет на полученный план, если «не связан» — значит не влияет. В нашем случае ресурс 1 и 4 имеют статус «не связан» — это значит, что эти ресурсы не ограничивают возможности в производстве, что не скажешь про ресурс 2 и 3, которые использованы полностью;
Разница между имеющемся в наличие количеством ресурсов и использованных при полученном плане.
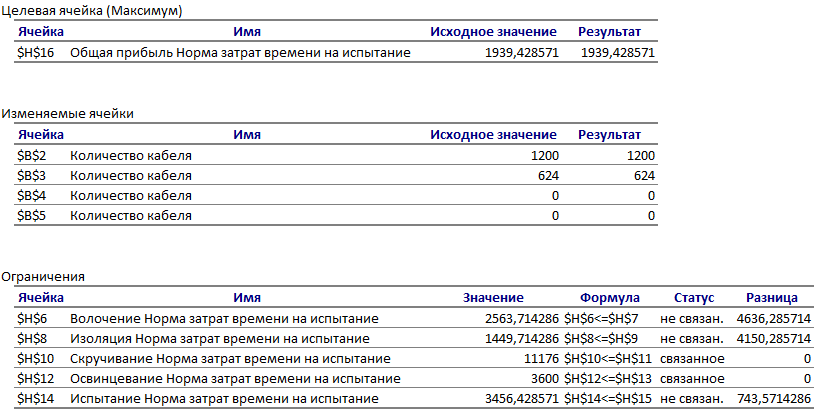
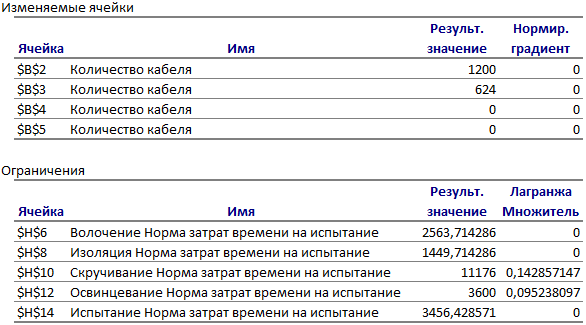
Отчет по устойчивости. В таблице Изменяемые ячейки этого отчета приведена информация о значениях изменяемых ячеек:
♦ адреса изменяемых ячеек;
♦ их имена (созданные заранее или составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки); если имен нет, то это поле остается пустым;
♦ значения переменных в этих ячейках, найденные средством Поиск решения;
♦ нормированная стоимость — это значение равно нулю, если значение соответствующей переменной находится в границах своего возможного изменения, но не достигает этих границ (учитываются границы, которые задаются явно в виде неравенств типа x ³ 0 и/или х £ 100). Если переменная равна значению одной из своих явно заданных границ (например, равна нулю при заданном условии неотрицательности), то значение нормированной стоимости показывает, насколько изменится значение целевой функции, если значение этой переменной увеличится на единицу1;
В таблице Ограничения приведена информация об ограничениях:
♦ адреса ячеек, на значения которых наложены ограничения;
♦ их имена (созданные заранее или составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки); если имен нет, то это поле остается пустым;
♦ значения в этих ячейках, найденные средством Поиск решения;
♦ теневая цена (Множитель Лагранжа) показывает, насколько изменится значение целевой функции, если на единицу изменится значение правой части данного ограничения; теневая цена отлична от нуля только тогда, когда данное ограничение в оптимальном решении является связанным (и решение не вырождено);
В отчете по пределам показано, в каких пределах с учетом всех ограничений могут изменяться переменные (значения в столбцах Верхний предел и Нижний предел) и какие при этом значения будет принимать целевая функция (значения в столбцах Целевой результат). Отметим, что если на значения переменной не налагаются явные ограничения, задающие ее верхнюю (или нижнюю) границу, то в столбцах Верхний предел и Целевой результат (или Нижний предел и Целевой результат) для этой переменной будут стоять значения ошибки #Н/Д.
Источник
Adblock
detector
| Общий фонд рабочего времени, ч | Нормы затрат времени, ч, на обработку 1 км кабеля вида | Общий фонд рабочего времени, ч | |||
| 1 | 2 | 3 | 4 | ||
| Волочение | 1,2 | 1,8 | 1,6 | 2,4 | 7200 |
| Наложение изоляции | 1,0 | 0,4 | 0,8 | 0,7 | 5600 |
| Скручивание элементов в кабель | 6,4 | 5,6 | 6,0 | 8,0 | 11176 |
| Освинцовывание | 3,0 | — | 1,8 | 2,4 | 3600 |
| Испытание и контроль | 2,1 | 1,5 | 0,8 | 3,0 | 4200 |
| Прибыль от реализации 1 км кабеля, рр. | 1,2 | 0,8 | 1,0 | 1,3 |
Министерство Образования
Российской Федерации
Южно-Уральский Государственный
Университет
Кафедра Системы Управления
КУРСОВАЯ РАБОТА
по дисциплине: Исследование
операций
Вариант 8
Руководитель:
Плотникова Н.В.
«___»__________2004 г.
Автор проекта:
студентка группы
ПС – 317
Куликова Мария
«___»__________2004 г.
Проект защищен
с оценкой
«___»__________2004 г.
Челябинск
2004 г.
Содержание.
Задача 1………………………………………………………………….3
Задача 2………………………………………………………………….8
Задача 3…………………………………………………………………10
Задача 4…………………………………………………………………13
Задача 1 (№8)
Условие:
На производстве четырёх
видов кабеля выполняется пять групп
технологических операций. Нормы затрат
на 1 км. кабеля данного вида на каждой
из групп операций, прибыль от реализации
1 км. каждого вида кабеля, а также общий
фонд рабочего времени, в течение которого
могут выполняться эти операции, указаны
в таблице.
Определить такой план выпуска
кабеля, при котором общая прибыль от
реализации изготовляемой продукции
является максимальной.
|
Технологическая |
Нормы затрат |
Общий |
|||
|
1 |
2 |
3 |
4 |
||
|
Волочение |
а11 |
а12 |
а13 |
а14 |
А1 |
|
Наложение |
а21 |
а22 |
а23 |
а24 |
А2 |
|
Скручивание |
а31 |
а32 |
а33 |
а34 |
А3 |
|
Освинцовывание |
а41 |
а42 |
а43 |
а44 |
А4 |
|
Испытание и |
а51 |
а52 |
а53 |
а54 |
А5 |
|
Прибыль от |
В1 |
В2 |
В3 |
В4 |
|
№вар. |
а11 |
а12 |
а13 |
а14 |
а21 |
а22 |
а23 |
а24 |
а31 |
а32 |
а33 |
а34 |
а41 |
|
1 |
1,5 |
1 |
2 |
1 |
1 |
2 |
0 |
2 |
4 |
5 |
5 |
4 |
2 |
|
№ вар. |
а42 |
а43 |
а44 |
а51 |
а52 |
а53 |
а54 |
А1 |
А2 |
А3 |
А4 |
5 |
|
1 |
1 |
4 |
0 |
1 |
2 |
1,5 |
4 |
6500 |
4000 |
11000 |
4500 |
4500 |
Решение:
Составляем математическую
модель задачи:
пусть x1 –длина 1-ого кабеля
(км);
x2 – длина 2-ого кабеля
(км);
x3 – длина 3-ого кабеля
(км);
x4 – длина 4-ого кабеля
(км)
тогда целевая функция L
— общая прибыль от реализации изготовляемой
продукции, будет иметь следующий вид
L=
В1×1
+ В2×2
+ В3×3
+ В4×4
= x1+
2×2
+ 1,5×3
+ x4
→ max
Получим систему ограничений:
1,5×1 + x2 + 2×3+ x4
6500;
x1 + 2×2 + 0x3+2×4
4000;
4×1 + 5×2 + 5×3+4×4 11000;
2×1 + x2 +1,5×3+0x4
4500;
x1 + 2×2 +1,5×3+4×4
4500.
Приведём полученную математическую
модель к виду ОЗЛП с помощью добавочных
неотрицательных переменных, число
которых равно числу неравенств:
1,5×1 + x2 + 2×3+ x4 + x5 =
6500;
x1 + 2×2 + 0x3+2×4 + x6=
4000;
4×1 + 5×2 + 5×3+4×4 + x7=11000;
2×1 + x2 +1,5×3+0x4 +
x8 =4500;
x1 + 2×2 +1,5×3+4×4 +
x9 =4500.
Итак, выберем x1, x2, x3, x4 —
свободными переменными, а x5, x6, x7, x8, x9 —
базисными переменными (каждая из них
встречаются в системе лишь в одном
уравнении с коэффициентом 1, а в остальных
с нулевыми коэффициентами). Приведём
систему к стандартному виду, выразив
для этого все базисные переменные через
свободные:
x5 = 6500 – (1,5×1
+ x2 + 2×3+ x4 );
x6 = 4000 – (
x1 + 2×2 + 0x3+2×4);
x7 =11000 — ( 4×1
+ 5×2 + 5×3+4×4);
x8 =4500 – ( 2×1
+ x2 +1,5×3+0x4);
x9 =4500 – (
x1 + 2×2 +1,5×3+4×4)
L=0
–(- x1-
2×2
— 1,5×3
— x4)
Решим методом симплекс-таблиц:
Это решение опорное, т.к. все
свободные члены положительны.
Выберем столбец в таблице, который
будет разрешающим, пусть это будет x1,
выберем в качестве разрешающего элемента
тот, для которого отношение к нему
свободного члена будет минимально (это
x8).
|
A |
|
|
|
|
|
|
L |
0 2250 |
-1 0,5 |
-2 0,5 |
-1,5 2 |
-1 0 |
|
|
6500 -3375 |
1,5 -0,75 |
1 -0,75 |
2 -3 |
1 0 |
|
|
4000 -2250 |
1 -0,5 |
2 -0,5 |
0 -2 |
3 0 |
|
|
11000 -9000 |
4 -2 |
5 -2 |
5 -8 |
4 0 |
|
x8 |
4500 2250 |
2 0,5 |
1 0,5 |
4 2 |
0 0 |
|
x9 |
4500 -2250 |
1 -0,5 |
2 -0,5 |
1,5 -2 |
4 0 |
Меняем
и
|
A |
x8 |
|
|
|
|
|
L |
2250 1000 |
0,5 -1 |
-1,5 0,5 |
0,5 -1,5 |
-1 2 |
|
|
3125 -500/3 |
-0,75 1/6 |
0,25 -1/12 |
-1 0,25 |
1 -1/3 |
|
|
1750 -1000 |
-0,5 1 |
1,5 -0,5 |
-2 1,5 |
3 -2 |
|
|
2000 2000/3 |
-2 -2/3 |
3 1/3 |
-3 -1 |
4 4/3 |
|
|
2250 -1000/3 |
0,5 1/3 |
0,5 -1/6 |
2 0,5 |
0 -2/3 |
|
x9 |
2250 -1000 |
-0,5 1 |
1,5 -0,5 |
-0,5 1,5 |
4 -2 |
Меняем
и x9
|
A |
x8 |
|
|
|
|
|
L |
3250 250 |
-0,5 0,5 |
0,5 -0,5 |
-1 1 |
1 2 |
|
|
8875/3 187,5 |
-7/12 0,375 |
-1/12 -0,375 |
-0,75 0,75 |
2/3 1,5 |
|
|
750 125 |
0,5 0,25 |
-0,5 -0,25 |
-0,5 0,5 |
1 1 |
|
|
2000/3 250 |
-2/3 0,5 |
1/3 -0,5 |
-1 1 |
4/3 2 |
|
|
5750/3 -625 |
5/6 -1,25 |
-1/6 1,25 |
2,5 -2,5 |
-2/3 -5 |
|
x9 |
250 250 |
0,5 0,5 |
-0,5 -0,5 |
1 1 |
2 2 |
|
A |
x8 |
|
x9 |
|
|
|
L |
3500 |
0 |
0 |
1 |
3 |
|
|
18875/6 |
-5/24 |
-11/24 |
0,75 |
13/6 |
|
|
875 |
0,75 |
-0,75 |
0,5 |
2 |
|
|
2750/3 |
-1/6 |
-1/6 |
1 |
10/3 |
|
|
3875/3 |
-5/12 |
13/12 |
-2,5 |
-17/3 |
|
|
250 |
0,5 |
-0,5 |
1 |
2 |
Видим, что коэффициенты при
переменных в целевой функции положительны,
значит, найденное решение будет
оптимальным.
Итак,
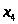
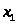
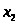
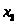
L=3500.
Ответ: если
предприятие будет изготавливать только
три вида проволоки 1,2,3 причем 3875/3 км,
2750/3 км, 250 км соответственно, то общая
прибыль от реализации изготовляемой
продукции будет максимальной и равной
3500(ед).
Задача 2 (№28)
Условие:
С помощью симплекс–таблиц
найти решение задачи линейного
программирования: определить экстремальное
значение целевой функции Q=CTx при условии
Ax
B,
где CT
= [
c1
c2
. . . c6
]T
, ВT
= [
b1 b2 . . . b6 ]T
,
XT
= [
x1
x2
. . . x6]T
, А= [aij]
(i=1,6;
j=1,3).
|
№ вар. |
с1 |
с2 |
с3 |
с4 |
с5 |
с6 |
b1 |
b2 |
b3 |
Знаки |
a11 |
a12 |
a13 |
a14 |
||
|
1 |
2 |
3 |
||||||||||||||
|
28 |
-6 |
0 |
|
-1 |
-1 |
0 |
8 |
|
|
= |
= |
= |
4 |
1 |
1 |
2 |
|
№ вар. |
a15 |
a16 |
a21 |
a22 |
a23 |
a24 |
a25 |
a26 |
a31 |
a32 |
a33 |
a34 |
a35 |
a36 |
Тип |
|
34 |
1 |
0 |
2 |
-1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
max |
Решение:
Получим систему:
4 x1 + x2 + x3+2×4 +
x5 =8;
2×1 — x2 +x4=2;
x1 + x2+x5=3
L=
-6×1+ x3 -x4 -x5 → max
Пусть x2, x4 – свободные
переменные, а x1, x3, x5 — базисные переменные.
Приведем систему и целевую функцию к
стандартному виду, для построения
симплекс-таблицы:
x5 =2-(1,5×2 -0,5 x4);
x3 =6-(1,5×2
+0,5 x4);
x1=1-(-0,5×2+0,5×4)
L=-2-(3×2-
x4) → max
Составим симплекс-таблицу:
Выберем разрешающим
столбцом x4,т.к. только перед этой
переменной в целевой функции отрицательное
число, выберем в качестве разрешающего
элемента тот, для которого отношение к
нему свободного члена будет минимально
(это x1). Меняем x4 и x1
-
b
x2
x4
L
-2
2
3
-1
-1
2
x1
1
2
-0,5
-1
0,5
2
1/0,5=2
6
-1
1,5
0,5
0,5
-1
6/0,5=12
2
1
1,5
-0,5
-0,5
1
-
b
x2
x1
L
0
2
2
x4
2
-1
2
5
2
-1
3
1
1
Получили оптимальное решение,
т.к. все коэффициенты положительны.
Итак, x1= x2=0, x3 =5,
x4=2, x5
=3, L=0.
Ответ: x1= x2=0,
x3 =5, x4=2,
x5 =3, L=0.
Задача 3 (№8)
Условие:
Решение транспортной задачи:
1.
Записать условия задачи в матричной
форме.
2. Определить опорный план задачи.
3. Определить оптимальный план
задачи.
4. Проверить решение задачи
методом потенциалов.
|
№вар. |
а1 |
а2 |
а3 |
b1 |
b2 |
b3 |
b4 |
b5 |
с11 |
с12 |
с13 |
|
8 |
200 |
200 |
600 |
200 |
300 |
200 |
100 |
200 |
25 |
21 |
20 |
|
с14 |
с15 |
с21 |
с22 |
с23 |
с24 |
с25 |
с31 |
с32 |
с33 |
с34 |
с35 |
|
50 |
18 |
15 |
30 |
32 |
25 |
40 |
23 |
40 |
10 |
12 |
21 |
Решение:
Составим
таблицу транспортной задачи. Заполним
таблицу методом северо-западного угла:
|
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
|
A1 |
25 200 |
21 |
20 |
50 |
18 |
200 |
|
A2 |
15 |
30 200 |
32 |
25 |
40 |
200 |
|
A3 |
23 |
40 100 |
10 200 |
12 100 |
21 200 |
600 |
|
bj |
200 |
300 |
200 |
100 |
200 |
1000 |
Количество заполненных
ячеек r=m+n-1=6.
Проверим сумму по столбцам, сумму
по строкам и количество базисных
(заполненных) клеток:
r
=6,
ai=
bj=1000,
всё выполняется, значит,
найденный план является опорным.
L=25*200+30*200+40*100+10*200+12*100+21*200=22400
Постараемся улучшить план
перевозок.
Рассмотрим
цикл (1;1)-(1;2)-(2;2)-(2;1)
Подсчитаем цену цикла:
j=15-30+21-25=-19<0
|
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
|
A1 |
25 |
21 200 |
20 |
50 |
18 |
200 |
|
A2 |
15 200 |
30 |
32 |
25 |
40 |
200 |
|
A3 |
23 |
40 100 |
10 200 |
12 100 |
21 200 |
600 |
|
bj |
200 |
300 |
200 |
100 |
200 |
1000 |
L=21*200+15*200+40*100+10*200+12*100+21*200=18600
Рассмотрим
цикл (2;1)-(2;2)-(3;2)-(3;1)
j=-15+30+23-40=-2<0
|
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
|
A1 |
25 |
21 200 |
20 |
50 |
18 |
200 |
|
A2 |
15 100 |
30 100 |
32 |
25 |
40 |
200 |
|
A3 |
23 100 |
40 |
10 200 |
12 100 |
21 200 |
600 |
|
bj |
200 |
300 |
200 |
100 |
200 |
1000 |
L=21*200+15*100+30*100+23*100+10*200+12*100+21*200=18400
Проверим
методом потенциалов:
Примем
α1=0, тогда βj
= cij
– αi
(для заполненных клеток).
Если
решение верное, то во всех пустых клетках
таблицы Δij
= cij
– (αi+
βj)
≥ 0
Очевидно,
что Δij
=0 для заполненных клеток.
В
результате получим следующую таблицу:
|
B1=6 |
B2=21 |
B3=-7 |
B4=-5 |
B5=4 |
ai |
|
|
A1=0 |
25-6>0 |
21-21=0 200 |
20+7>0 |
50+5>0 |
18-4>0 |
200 |
|
A2=9 |
15-9-6=0 100 |
30-21-9=0 100 |
32-9+7>0 |
25+5-9>0 |
40-4-9>0 |
200 |
|
A3=17 |
23-17-6=0 100 |
40-21-17>0 |
10+7-17=0 200 |
12+5-17=0 100 |
21-4-17=0 200 |
600 |
|
bj |
200 |
300 |
200 |
100 |
200 |
1000 |
Таким образом, решение
верное, т.к. Δij
> 0 для всех пустых клеток и Δij
=0 для всех заполненных.
Тогда сумма всех перевозок:
L=18400
Ответ:
|
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
|
A1 |
25 |
21 200 |
20 |
50 |
18 |
200 |
|
A2 |
15 100 |
30 100 |
32 |
25 |
40 |
200 |
|
A3 |
23 100 |
40 |
10 200 |
12 100 |
21 200 |
600 |
|
bj |
200 |
300 |
200 |
100 |
200 |
1000 |
Задача 4
(№53)
Условие:
Определить экстремум целевой
функции вида
F
= c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях:
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2.
Найти
стационарную точку целевой функции и
исследовать ее (функцию) на выпуклость
(вогнутость) в окрестностях стационарной
точки.
Составить
функцию Лагранжа.
Получить
систему неравенств в соответствии с
теоремой Куна-Таккера.
Используя
метод искусственных переменных составить
симплекс-таблицу и найти решение
полученной задачи линейного
программирования.
Дать
ответ с учетом условий дополняющей
нежесткости.
|
№ |
b1 |
b2 |
c11 |
c12 |
c22 |
extr |
a11 |
a12 |
a21 |
a22 |
p1 |
p2 |
Знаки огр. 1 2 |
|
|
53 |
6 |
1,5 |
-2 |
-4 |
–1 |
max |
2,5 |
-1 |
3 |
2,5 |
7 |
13 |
|
|
Решение:
Целевая функция:
F=
-2×12-x22-4x1x2+6×1+1,5×2→max
Ограничения g1(x)
и g2(x):
2,5×1-x27
2,5×1-x2–70
3×1+2,5×213 3×1+2,5×2-130
1) определим относительный
максимум функции, для этого определим
стационарную точку (х10, х20):
→
2) Исследуем стационарную точку
на максимум, для чего определяем
выпуклость или вогнутость функции
F11
(х10, х20) = -4 < 0
F12
(х10, х20)=-4
F21
(х10, х20)=-4
F22
(х10, х20)=-2
F11
F12 -4
-4
F21
F22
-4 -2
Т.к. условие выполняется, то
целевая функция является строго выпуклой
в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2×12-x22-4x1x2+6×1+1,5×2+u1
(2,5×1-x2–7)+
u2 (3×1+2,5×2-13).
Получим уравнения седловой
точки, применяя теорему Куна-Таккера:
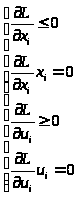
Объединим неравенства в систему
А, а равенства в систему В:
Система А:
Система В:
Перепишем систему А:
6-4×1-4×2+2,5u1+3u2
<0
1,5-4×1-2×2-u1+2,5u2
<0
2,5×1-x2–70
3×1+2,5×2–130
4)Введем новые переменные
V={v1,v2}≥0;
W={w1,w2}≥0
в систему А для того, чтобы
неравенства превратить в равенства:
6-4×1-4×2+2,5u1+3u2
+ v1=0
1,5-4×1-2×2-u1+2,5u2
+ v2=0
2,5×1-x2–7-
w1=0
3×1+2,5×2–13-
w2=0
Тогда
— v1=6-4×1-4×2+2,5u1+3u2
—
v2=1,5-4×1-2×2-u1+2,5u2
w1=2,5×1-x2–7
w2=3×1+2,5×2–13
Следовательно, система В примет
вид:
— это условия дополняющей
нежесткости.
5) Решим систему А с помощью метода
искусственных переменных.
Введем переменные Y={y1;
y2}
в 1 и 2 уравнения системы
6-4×1-4×2+2,5u1+3u2
+ v1 -y1=0
1,5-4×1-2×2-u1+2,5u2
+ v2 -y2=0
2,5×1-x2–7-
w1=0
3×1+2,5×2–13-
w2=0
и создадим псевдоцелевую
функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных
выберем х1, х2, v1,
v2,
u1,
u2;
а в качестве базисных y1,
y2,
w1,
w2.
Приведем систему и целевую
функцию к стандартному виду, для
построения симплекс-таблицы:
y1=6-(4×1+4×2-2,5u1-3u2
—
v1)
y2=1,5-(4×1+2×2+u1-2,5u2
-v2)
w1=-7-(-2,5×1+x2)
w2=-13-(-3×1-2,5×2)
Y’=-Y=-My1-My2=-7,5M-(-8×1-6×2+1,5u1+5,5u2+
v1+v2) M
Решим с помощью симплекс-таблицы.
Найдем опорное решение:
|
|
|
|
|
|
|
|
|
|
|
-7,5M 4,5M |
-8M 12M |
-6M 3M |
1,5M 3M |
5,5M -7,5M |
M 0 |
M -3M |
|
|
6 -3 |
4 -8 |
4 -2 |
-2,5 -2 |
-3 5 |
-1 0 |
0 2 |
|
|
1,5 3/4 |
4 2 |
2 0,5 |
1 0,5 |
-2,5 -5/4 |
0 0 |
-1 -0,5 |
|
|
-7 -3/4 |
-2,5 -2 |
1 -0,5 |
0 -0,5 |
0 5/4 |
0 0 |
0 0,5 |
|
|
-13 15/8 |
-3 5 |
-2,5 5/4 |
0 5/4 |
0 -25/16 |
0 0 |
0 -5/4 |
Меняем
и
|
|
|
|
|
|
|
|
|
|
|
-3M 3M |
4M -4M |
3M -2M |
4,5M -4,5M |
-2M M |
M -M |
-2M 2M |
|
|
3 3/2 |
-4 -2 |
-2 -1 |
-4,5 -9/4 |
2 0,5 |
-1 -0,5 |
2 1 |
|
|
3/4 15/8 |
2 -2,5 |
0,5 -5/4 |
0,5 -45/16 |
-5/4 5/8 |
0 -5/8 |
-0,5 5/4 |
|
|
-31/4 -15/8 |
-4,5 2,5 |
-0,5 5/4 |
-0,5 45/16 |
5/4 -5/8 |
0 5/8 |
0,5 -5/4 |
|
|
-89/8 75/32 |
2 -25/8 |
5/4 -25/16 |
5/4 -225/64 |
-25/16 25/32 |
0 -25/32 |
-5/4 25/16 |
Меняем
и
|
|
|
|
|
|
|
|
|
|
|
0 0 |
0 0 |
M 0 |
0 0 |
M 0 |
0 0 |
0 0 |
|
|
3/2 77/8 |
-2 -1 |
-1 -3/4 |
-9/4 -37/16 |
0,5 5/8 |
-0,5 -5/8 |
1 3/4 |
|
|
21/8 77/32 |
-0,5 -1/4 |
-3/4 -3/16 |
-37/16 -37/64 |
5/8 5/32 |
-5/8 -5/32 |
3/4 -3/16 |
|
|
-77/8 77/16 |
-2 -0,5 |
3/4 -3/8 |
37/16 -37/32 |
-5/8 5/16 |
5/8 -5/16 |
-3/4 3/8 |
|
|
-281/32 693/128 |
-9/8 -9/16 |
-5/16 -27/64 |
-145/64 -333/256 |
25/32 45/128 |
-25/32 -45/128 |
5/16 27/64 |
Меняем
и
|
|
|
|
|
|
|
|
|
|
|
0 0 |
0 0 |
M 0 |
0 0 |
M 0 |
0 0 |
0 0 |
|
|
89/8 431/18 |
-1 -16/9 |
-7/4 |
-73/16 |
9/8 |
-9/8 |
7/4 |
|
|
161/32 431/72 |
-1/4 -4/9 |
-15/16 |
-185/64 |
25/32 |
-25/32 |
9/16 |
|
|
77/16 431/36 |
-0,5 -8/9 |
-3/8 |
-37/32 |
5/16 |
-5/16 |
3/8 |
|
|
-431/32 431/18 |
-9/16 -16/9 |
-47/64 |
-913/256 |
145/128 |
-145/128 |
47/64 |
Меняем
и
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
M |
0 |
M |
0 |
0 |
|
|
2525/72 |
||||||
|
|
3173/288 |
||||||
|
|
2417/144 |
||||||
|
|
431/18 |
Итак,
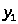
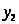
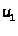
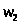
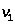
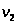
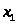
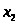
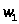
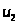
6) Условия дополняющей
нежесткости выполняются
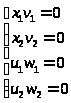
решения исходной задачи квадратичного
программирования существует.
Ответ: существует.
Литература.
1) Курс лекций Плотникова Н.В.
2) Пантелеев А.В., Летова Т.А.
«Методы оптимизации в примерах и
задачах».