Практическая работа в excel по системам счисления

Работа в Excel «Системы счисления»

1. Создайте таблицу степеней (от 1 до 10 степени) в Excel для чисел от 1 до 20 с помощью автоматического заполнения ячеек. Лист с таблицей степеней назовите «СТЕПЕНИ» и выделите голубым цветом.

2. На новом листе создайте таблицу соответствия чисел в различных системах счисления для систем с q= 10,2,8,16 с помощью автоматического заполнения ячеек (применяя формулы =ДЕС.В.ДВ / =ДЕС.В.ВОСЬМ/ =ДЕС.В.ШЕСТН) для чисел от 0 до 100. Лист с таблицей назовите «ТАБЛИЦА» и выделите красным цветом.

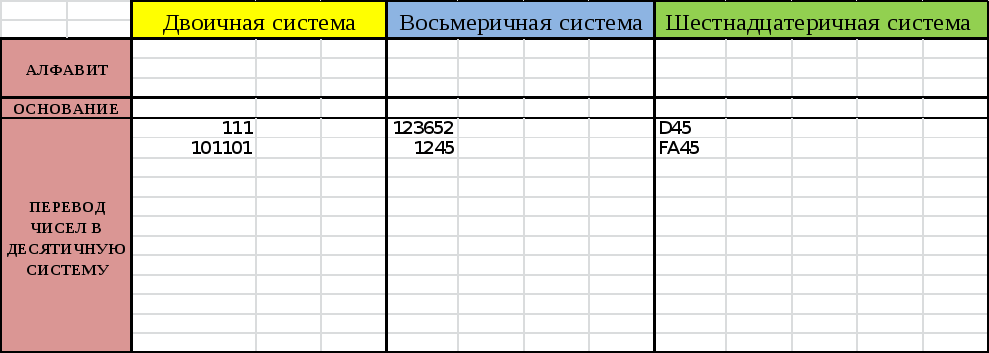
3. На новом листе создайте таблицу с алфавитами и основаниями систем счисления (заполните указанную таблицу):

Ниже на листе переведите указанные числа в десятичную систему счисления с помощью алгоритма. Проверьте себя формулами Excel. Лист с расчетами назовите «РЕШЕНИЕ» и выделите розовым цветом.

4. На новом листе «НОВАЯ ТЕМА» зеленого цвета создайте таблицу и переведите с помощью формул Excel указанные двоичные числа в восьмеричную и шестнадцатеричную системы:

Ниже запишите первое число 100101 по ячейкам (каждая цифра в одной ячейке – итого 6 ячеек). Справа налево разбейте данное число на триады:

Найдите на листе ТАБЛИЦА соответствие двоичных чисел 100 и 101 восьмеричным числам и запишите их в том же порядке. Проверьте, сходится ли результат с расчетом Excel. Переведите таким способом все остальные числа в восьмеричную систему счисления.

5. На этом же листе ниже переведите все двоичные числа в шестнадцатеричную систему счисления используя тот же принцип, только делением на тетрады (тетра — с греч. — группа из четырёх). Проверьте с решением Excel.

6*. Закодируйте шестнадцатеричным кодом изображение:

«Системы счисления» – базовая тема в курсе информатики. Изучение данной темы формирует у учащихся представление о математических основах информатики. Однако, здесь много теории, практическая работа обычно сводится к записям и выполнению упражнений в тетрадях. Это утомляет учащихся, снижает интерес и активность работы, а значит, понижается результативность урока. Применение такого мощного инструмента, каким являются электронные таблицы MS Excel, в среде которых создан Практикум, делает практическую работу более живой, повышает мотивацию к изучению, теоретический материал становится более понятным. Вместе с этим расширяется представление о практическом использовании электронных таблиц, закрепляются навыки работы с формулами в MS Excel. Практикум разработан мною ещё в 2003-2004 уч. году. Пользуюсь им каждый учебный год до настоящего времени.

Теоретическая часть темы в данной статье не рассматривается – считаю, что она хорошо известна во всех деталях всем, кто интересуется этой темой. Практикум представляет собой 6 файлов для демонстрации и практической работы в основных позиционных системах счисления

• Перевод_10_2.xls – перевод из десятичной системы счисления в двоичную;
• Перевод_10_8.xls – перевод из десятичной системы счисления в восьмеричную;
• Перевод_10_16.xls – перевод из десятичной системы счисления в шестнадцатеричную;
• Перевод_2_10.xls – перевод из двоичной системы счисления в десятичную;
• Перевод_8_10.xls – перевод из восьмеричной системы счисления в десятичную;
• Перевод_16_10.xls– перевод из шестнадцатеричной системы счисления в десятичную (см. папки Приложение_1 и Приложение_2).

Все файлы организованы единообразно.

Рассмотрим организацию и технологию использования на примере файла Перевод_10_2.xls (Приложение_1).

Файл включает 4 листа:

1 лист – Тренажёр_10_2, используется для первоначальной тренировки перевода;

2 лист – Копия_ Тренажёр_10_2, – используется для более детального разбора примера с 1 листа, если учащиеся не поняли смысл и содержание технологии перевода на листе 1;

3 лист – собственно практическая работа, содержит 8 упражнений;

4 лист – справочная информация.

1 лист – Тренажёр_10_2

На листе две таблицы – основная и дополнительная. В основной таблице в яч.D6 записано число в десятичной системе счисления, которое следует перевести в двоичную систему. В яч. E6 будет помещён результат перевода. Столбцы A, B, C отведены для выполнения процесса перевода. Принцип перевода классический – последовательное целочисленное деление на 2 с остатками.

В ячейку А5 копируется переводимое число из яч.D6 (или вписывается вручную). В яч. B5 помещен делитель.

<Рисунок_1>

Ячейки А6 и С5 содержат формулы, помечены заливкой, уничтожение формул недопустимо! (при нечаянном уничтожении формул файл необходимо скопировать с исходной версии и работу начать заново). В яч.В5 записан делитель 2.

Перевод основан на свойстве копирования формул в электронных таблицах и осуществляется в последовательности:

1. в яч.А5 вносим число 365;
2. в яч А6 появляется первое частное (общий «бумажный» принцип перевода представлен для сравнения в дополнительной таблице, такие таблицы приводятся практически в любом учебном пособии);
3. при помощи маркера ячейки А6 копируем формулу по столбцу А вниз до появления первого 0, появление первого 0 означает, что все частные получены;
4. яч.В5 с делителем не изменяется;
5. в яч. С5 уже получен первый остаток, при помощи маркера яч. С5 копируем формулу по столбцу С вниз до появления первого 0, появление первого 0 означает, что все остатки получены;
6. перевод произведён,

Результат получается при последовательной записи снизу вверх всех цифр остатков в яч.Е6 (стрелка для подсказки).

Более подробно эта технология представлена на Листе 2 – Копия_ Тренажёр_10_2.

<Рисунок_2>

Переходим на лист «практ_работа_10_2». Перевод всех чисел выполняется аналогично. Удалять и очищать рабочие ячейки нет надобности, т.к. каждый раз при внесении нового числа в яч.А5 происходит автоматический перерасчёт содержимого уже использованных ячеек, а если ячеек недостаточно (а это видно в столбце А при расчете частных и в столбце С при расчёте остатков) необходимо просто докопировать соответствующие формулы до получения первого 0.

По завершении перевода учащиеся могут открыть приложение «Калькулятор» и проверить правильность своей работы.

Аналогично выполняется работа с файлами Перевод_10_8.xls и

Перевод_10_16.xls . Для записи чисел в шестнадцатеричной системе учащиеся должны воспользоваться листом Информация.

Рассмотрим организацию и технологию «обратного» перевода на примере файла Перевод_2_10.xls (Приложение_2)

Файл аналогично содержит 4 листа.

<Рисунок_3>

1 лист – Тренажёр_2_10

Число в двоичной системе счисления для перевода записано в яч.F6. В соответствии с математической записью перевода в столбце B записаны номера разрядов, а в столбце C – веса разрядов, в столбец D будут вноситься разрядные коэффициенты, разрядные слагаемые формируются по формулам в столбце E. Итог – в яч.E19 суммированием ячеек диапазона E6:E18 получается эквивалент двоичного числа – десятичное число.

Технология перевода:

1. копируем число из яч.F6 в яч.A6;
2. в направлении снизу вверх (по стрелке) от яч.D18 выписываем все разрядные коэффициенты двоичного числа, т.е. от младшего разряда к старшему;
3. в столбце E в ячейку E12 вносим формулу =D12*C12 , формулу копируем в ячейки диапазона E13:E18 ;
4. суммируем ячейки диапазона E12:E18;
5. результат записываем в яч.G6

<Рисунок_4>

После освоения тренажёрного варианта переходим на лист практической работы. Замечу, что я преднамеренно не внесла заранее соответствующие формулы в ячейки диапазона E12:E19. Считаю, что на этом этапе надо предоставить возможность учащимся самостоятельно поработать с формулами.

По завершении перевода учащиеся могут открыть приложение «Калькулятор» и проверить правильность своей работы.

Аналогично выполняется работа с файлами Перевод_8_10.xls и

Перевод_16_10.xls . Одно небольшое отличие заключается в том, что при работе с файлом Перевод_16_10.xls вводится дополнительный столбец, в котором учащиеся должны переписать разрядные коэффициенты чисел в шестнадцатеричной системе от A до F в десятичном значении, при этом учащиеся должны воспользоваться листом Информация.

Возможно, такой Практикум покажется громоздким. Однако, мне это помогает проводить уроки более динамично, повышать мотивацию к изучению темы, добиваться понимания материала темы.

Тема:
Перевод и арифметика в позиционных системах счисления с помощью таблиц Excel.

Цель
урока:

• систематизировать
  и обобщить знания учащихся, полученные при изучении темы “Арифметические
  операции в позиционных системах счисления” и пр.“Microsoft Office Excel”;
• показать
  применение компьютера для математических вычислений;
• развивать
  навыки реализации теоретических знаний в практической деятельности;
• расширять
  кругозор и развивать логическое мышление учащихся в области информатики.

Задачи
урока: закрепить умения решать задачи на перевод чисел из одной системы
счисления в другую, производить арифметические операции над числами, работать с
пр. “Microsoft Office Excel”.

К
этому уроку учащиеся знают:

• Что такое
  “электронные таблицы”, их виды, функции; назначение. Интерфейс табличного
  процессора Microsoft Excel.
• Арифметические
  действия в двоичной, восьмеричной, шестнадцатеричной системах счисления.

Основные
умения:

• Умеют
  составлять и заполнять таблицы.
• Умеют
  использовать формулы для арифметических вычислений в Microsoft Excel.
• Умеют
  переводить числа из одной системы счисления в другую.

Тип
урока: урок с применением современных информационных технологий.

Оборудование: Комплексно-методическое
обеспечение: компьютеры, программное обеспечение (Microsoft Office Excel).

Форма: комбинированный
урок.

Методы
обучения: объяснительно-демонстрационные, практические.

Межпредметные
связи: информатика, математика.

Ход
урока:

      
I.           
Орг. момент (3 мин).

    II.           
Сообщение темы, целей и задач урока (2 мин).

 III.           
Практическая работа за компьютером.

IV.           
Подведение итогов и домашнее задание.

Приветствие
учителя и учеников, проверка готовности учащихся к уроку
(подготовка рабочего места).

Потребность в счете у
человека возникла еще в древние времена. Для сохранения результатов подсчетов
сначала люди использовали засечки, зарубки, рисунки. Понадобился не один
десяток веков, пока люди придумали числа для обозначения количества и научились
с ними работать. Сейчас, используя компьютерные технологии, можно намного
облегчить эту работу. И сегодня мы убедимся в этом.

В позиционной системе
счисления любое число представляется в виде последовательности цифр,
количественное значение которых зависит от места (позиции), которое занимает
каждая из них в числе. Алфавит десятичной системы состоит из десяти символов:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемых арабским цифрами. По правилам этой
системы счисления символы располагаются, начиная с нулевой позиции и далее по
возрастающей слева направо. Символ 1 в нулевой позиции – это единица, а в
первой позиции – это уже 10 единиц.

Для человеческого
восприятия числа, записанные в двоичной системе, выглядят однообразными.
Например, 9999₁₀ = 10011100001111_{2 .} Длинные
последовательности нулей и единиц плохо воспринимаются и запоминаются. Чтобы
получить более короткую и удобную запись, используют шестнадцатеричную или
восьмеричную систему. Эти основания тесно связаны с двойкой: 16=2⁴, 8=2³.

Объявление
темы урока: перевод чисел из одних систем счисления в другие и
арифметические действия с помощью пр. Microsoft Office Excel.

Вспомним системы
счисления: двоичную, восьмеричную, шестнадцатеричную, которые изучали в 9-м
классе.

Выполнение
арифметических действий в разных системах счисления

Арифметические действия
над числами, записанными с помощью позиционной системы счисления, производятся
по тем же правилам, что и в десятичной системе. Эти действия основаны на
одинаковых правилах действий над многочленами. Следствием этих правил являются
специфические таблицы сложения и умножения для заданной системы счисления.
Чтобы построить

такие таблицы, можно
воспользоваться таблицами для Десятичной системы, переведя число в каждой
ячейке в нужную систему счисления. Применяя подобные таблицы, можно выполнять
арифметические действия с многозначными числами, используя стандартные приемы
поразрядных действий (“в столбик”). В частности, сохраняются правила “переноса”
значения в следующий разряд и “заимствования” значения из старшего разряда при
сложении и вычитании. Если требуется выполнить арифметические действия с
числами, заданными в разных системах счисления, сначала надо преобразовать
данные числа к одной системе счисления, а затем выполнять действия.

Таблица
соответствия знаков в десятичной и двоичной системах счисления.

Давайте, ребята,
построим таблицы соответствия, воспользовавшись пр. “Microsoft Office Excel”.
Столбцы слева (синие цифры) – в10-ой системе счисления, заполняем,
воспользовавшись автозаполнением. Столбцы справа (черные цифры)– вручную,
вспоминая закономерности числообразования в двоичной системе счисления.

Приложение
1

По этой таблице за
секунды можно перевести число из десятичной системы в двоичную, и наоборот.
Вдобавок таблицу можно легко продолжить.

Арифметические
действия в двоичной системе.

Приложение
2

Простота этих таблиц
благоприятно сказывается на выполнении действий при помощи компьютера. В
частности, умножение сводится к операциям сложения. Посчитать несколько
примеров, результаты сложения и умножения проверить по таблице в Приложении
1.

Таблица
соответствия знаков в десятичной и восьмеричной системах счисления.

Столбцы слева (синие
цифры) – в10-ой системе счисления, заполняем, воспользовавшись автозаполнением.
Столбцы справа (черные цифры) – автозаполнением, вспоминая закономерности
числообразования в восьмеричной системе счисления.

Приложение
3

Арифметические
действия в восьмеричной системе.

Строим таблицы сложения
и умножения в десятичной системе счисления. Присваиваем следующим ячейкам
уникальные имена, чтобы их значения не менялись при автозаполнении: B1=пост0,
C1=пост1, D1=пост2, E1=пост3, F1=пост4, G1=пост5, H1=пост6, I1=пост7. Вводим
формулы в соответствующие ячейки B2=A2+пост0, C2=А2+пост1, D2=A2+пост2,
E2=A2+пост3, F2=A2+пост4, G2=A2+пост5, H2=A2+пост6, I2=A2+пост7. Аналогичные
действия производим в ячейках К2-R2, заменив “+” на “*”. Выделяем полученные
значения и автозаполнением продолжаем до конца таблицы.

Приложение
4

В этой таблице нам
осталось заменить числа от 8 до 49 в десятичной системе на соответствующие им в
восьмеричной системе, воспользовавшись таблицей в Приложении
3.
В результате получаем таблицу в Приложении
5:

По этой таблице за
секунды можно посчитать сумму и произведение любых чисел в восьмеричной системе
счисления.

Таблица
соответствия знаков в десятичной и шестнадцатеричной системах счисления.

Столбцы слева (синие
цифры) – в10-ой системе счисления, заполняем, воспользовавшись автозаполнением.
Столбцы справа (черные цифры) – автозаполнением, вспоминая закономерности
числообразования в шестнадцатеричной системе счисления.

Приложение
6

Перевод
из одной системы счисления в другую.

При переводе чисел из
системы счисления с основанием р в десятичную систему
применяют развернутую форму записи,представляя основание
системы счисления и все цифры в десятичной системе. Полученное выражение
вычисляют по правилам десятичной арифметики. В результате получится запись
заданного числа в десятичной системе счисления. Например:

ЗЕ, С8₁₆ =3₁₆*10₁₆¹+ Е₁₆*10₁₆ ⁰ + С₁₆ *10₁₆ ^-1 + 8₁₆ *10₁₆ ^-2 =
3*16 + 14*1 + 12*16 ^-1 + 8*16 ^-2 = 48
+ 14 + 0,75 + 0,03125 = 62,78125₁₀.

Перевод
из двоичной системы в десятичную систему счисления.

Воспользовавшись
формулой в пр. “Microsoft Office Excel”, можно перевести числа за считанные
секунды, достаточно один раз ввести формулу в ячейке L1:
=A1*2^8+B1*2^7+C1*2^6+D1*2^5+E1*2^4+F1*2^3+G1*2^2+H1*2^1+I1*2^0, остальные
значения можно получить автозаполнением.

Приложение
7

Перевод
из восьмеричной системы в десятичную систему счисления.

Формула в ячейке F1:
=A1*8^2+B1*8^1+C1*8^0.

Приложение
8

Перевод
из шестнадцатеричной системы в десятичную систему счисления.

Формула в ячейке M1:
=G1*16^3+H1*16^2+I1*16^1+J1*16^0.

Приложение
9

Итоги
урока и домашнее задание:

• Сегодня мы
  научились переводить числа из системы счисления с основанием 2, 8, 16 в
  десятичную систему при помощи формул в Excel. Подумайте, какие формулы в
  Excel нужно использовать для перевода из десятичной системы в систему
  счисления с основанием 2, 8, 16?

• Попробуйте
  составить таблицы сложения и умножения для шестнадцатеричной системы
  счисления.

Опорный конспект урока (для учащегося).

Тема урока: «Перевод целых чисел в различных системах счисления с помощью Microsoft Office Excel».

Практическая работа №1: «Создание «Калькулятора» для перевода целых чисел из 10-ной системы счисления в любую другую систему счисления (меньше 10), используя табличный процессор Excel.»

Практическая работа №2: «Создание «Калькулятора» для перевода целых чисел из любой системы счисления в 10-ную систему счисления, используя табличный процессор Excel.»

Цели урока: (сформулировать самостоятельно) ________________________________________ ________________________________________________________________­­­­­­­­­­________________________

________________________________________________________________________________________ ________________________________________________________________________________________

Основные понятия на уроке:

1. Что называется системой счисления?

2. На какие две группы делятся все системы счисления?

3. Приведите примеры систем счисления.

4. Дайте определение табличному процессору.

5. Что называется электронной таблицей?

6. Назовите основные возможности программы MS Excel?

7. С какими данными работает электронная таблица?

8. Что называется ссылкой? Назовите виды ссылок.

9. Чем отличаются друг от друга абсолютная и относительная адресация ячеек?

10. Что называется формулой?

11. Что называется функцией?

12. Способы ввода функции?

13. Алгоритм перевода чисел в различных системах счисления.

Комментарии:

В кодировке латинских символов код букв A, B, C, D, E, F отличается на число 55 от их числовых значений в шестнадцатеричной системе счисления.

Например,

код буквы F равен 70, а числовое значение F равно 15

E 69, E 14

D 68, D 13

C 67, C 12

B 66, B 11

A 65, A 10

Поэтому при вычислениях в эл. таблицах, используем логическую функцию перевода кода в числовое значение «=ЕСЛИ(КОДСИМВ(аргумент)

Аргумент – это адрес ячейки числа

Вспомнить правила Т.Б за компьютером

Выполнение практической работы

Тестирование программы

Итог урока (Сделайте вывод о том, достигли ли вы цели, которую поставили перед собой в начале урока, что вам удалось, на каком этапе и с какими трудностями вы столкнулись.)

Функция ОСНОВАНИЕ выполняет преобразование числового значение в указанную систему счисления (двоичная, восьмеричная, шестнадцатеричная и т. д.) и возвращает соответствующий результат в виде текстовой строки.

Примеры использования функции ОСНОВАНИЕ в Excel

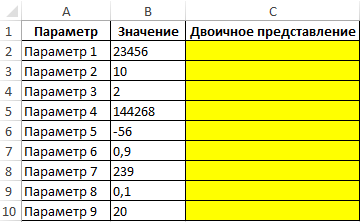
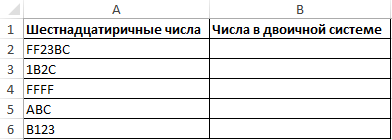
Пример 1. Для хранения чисел в БД удобно использовать их представление в двоичной системе счисления. Выполнить преобразование представленных значений.

Исходная таблица:

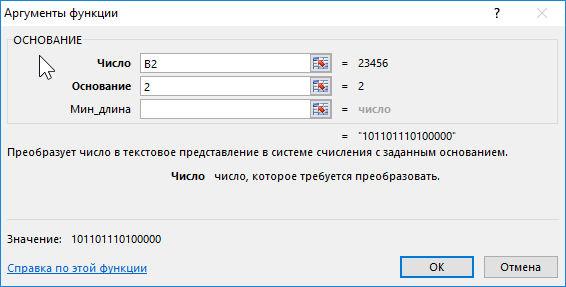
Для преобразования используем формулу:

Описание аргументов:

• B2 – число, которое требуется преобразовать;
• 2 – указатель вида системы счисления.

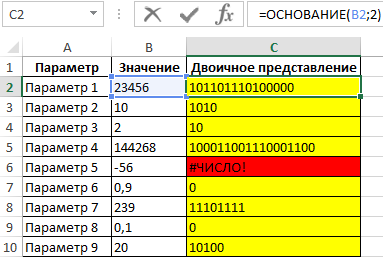
Выполним преобразование для всех чисел. Полученный результат:

Ошибка #ЧИСЛО! Возникла потому, что -56 находится вне диапазона допустимых значений (отрицательное число). Результат вычисления формулы =ОСНОВАНИЕ(0,9;2) эквивалентен результату =ОСНОВАНИЕ(0;2), поскольку рассматриваемая функция усекает дробные значения аргумента число до целых значений.



Перевод числа из одной системы счисления в другую в Excel

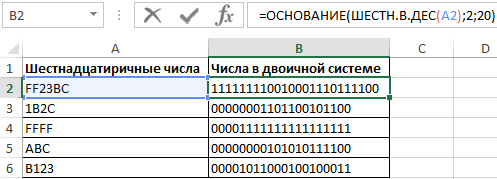
Пример 2. Преобразовать числа, записанные в шестнадцатеричной системе счисления в двоичную систему с длиной полученной строки не менее 20 символов.

Таблица значений:

В Excel предусмотрена формула ШЕСТН.В.ДВ, однако она поддерживает значения из диапазона от FFFFFFFE00 до 1FF. Поэтому выполним промежуточное преобразование в десятичную систему и воспользуемся функцией ОСНОВАНИЕ для перевода в двоичную:

Описание аргументов:

• ШЕСТН.В.ДЕС(A2) – исходное число, преобразованное в десятичную систему счисления;
• 2 – указание на вид системы счисления;
• 20 – минимальное количество символов в возвращаемой строке.

Результаты расчетов:

Сложение чисел в разных системах счисления в Excel

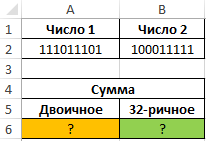
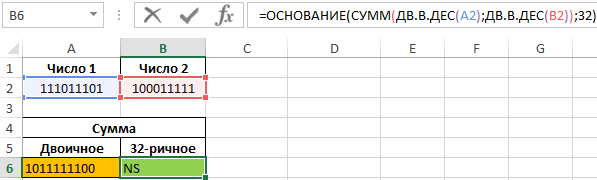
Пример 3. Отобразить результаты сложения двух чисел, записанных в двоичной системе, в виде чисел в десяти- и тридцатидвухричных системах счисления.

Исходная таблица:

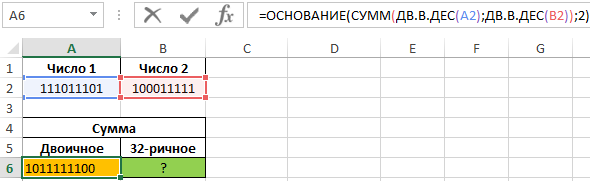
В ячейке A6 запишем следующую формулу:

Функция ДВ.В.ДЕС преобразует числа из двоичной в десятеричную систему.

В ячейке B6 запишем формулу:

В данном способе выполняется преобразование в понятную многим десятичную систему счисления, в которой и выполняется операция сложения чисел (вместо, например, алгоритма сложения в столбик в двоичной системе, где необходимо учитывать правила: 0+0=0, 1+1=10 и т. д.). Функцией ОСНОВАНИЕ выполняется преобразование результата в требуемые системы исчисления. Пример расчета:

Особенности использования функции ОСНОВАНИЕ в Excel

Функция имеет следующую синтаксическую запись:

=ОСНОВАНИЕ(число;основание;[минимальная_длина])

Описание аргументов:

• число – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 0 до 253, которое требуется преобразовать к указанной системе счисления.
• основание – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 2 до 36, которое является основанием требуемой системы исчисления.
• [минимальная_длина] – необязательный аргумент, характеризующий числовое значение из диапазона от 0 до 255, определяющее минимальную длину в символах возвращаемой текстовой строки.

Примечания:

1. Функция возвращает код ошибки #ЧИСЛО!, если любой из ее аргументов является числовым значением, выходящим за пределы допустимых для данного аргумента значений.
2. Если один или несколько аргументов являются текстовой строкой, рассматриваемая функция вернет код ошибки #ЗНАЧ!.
3. Функция доступна только в новых версиях программы (Excel 2013 и более поздних).
4. В отличие, например, от функции ДЕС.В.ДВ, которая выполняет преобразование чисел из диапазона от -512 до 511, функция ОСНОВАНИЕ выполняет преобразование чисел от 0 до 2⁵³.
5. При явном указании аргумента [минимальная_длина] возможны следующие ситуации:

• длина полученного значения меньше, чем регламентируется аргументом [минимальная_длина]. В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины;
• длина рассчитанного значения больше, чем регламентируемая. Функция ОСНОВАНИЕ вернет полученный результат, не урезая его. Например, функция с аргументами (12345;2;20) вернет значение «00000011000000111001», а функция с аргументами (12345;2;2) вернет «11000000111001».