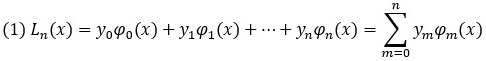
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
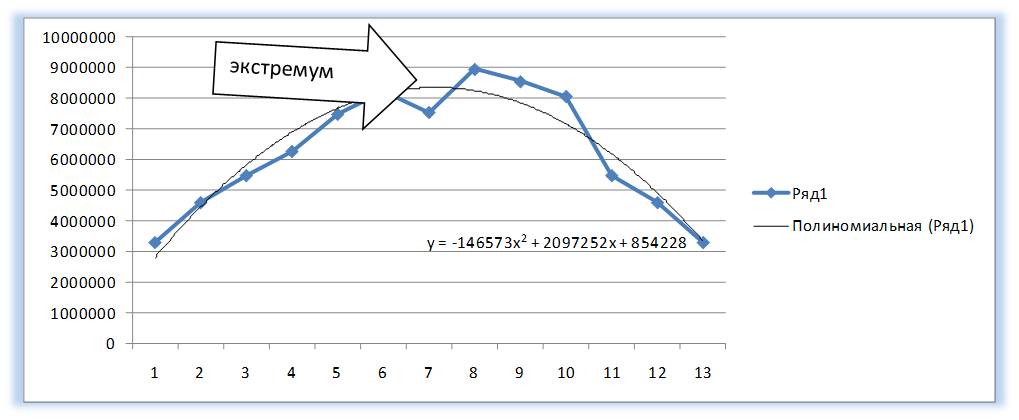
Что такое полином? Полином — это степенная функция y=ax2+bx+c (полином второй степени) и y=ax3+bx2+cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
У полинома второй степени y=ax2+bx+c один экстремум (на графике ниже 1 максимум).
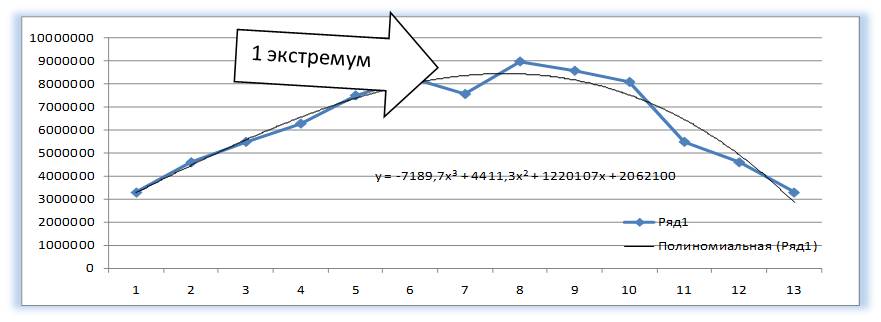
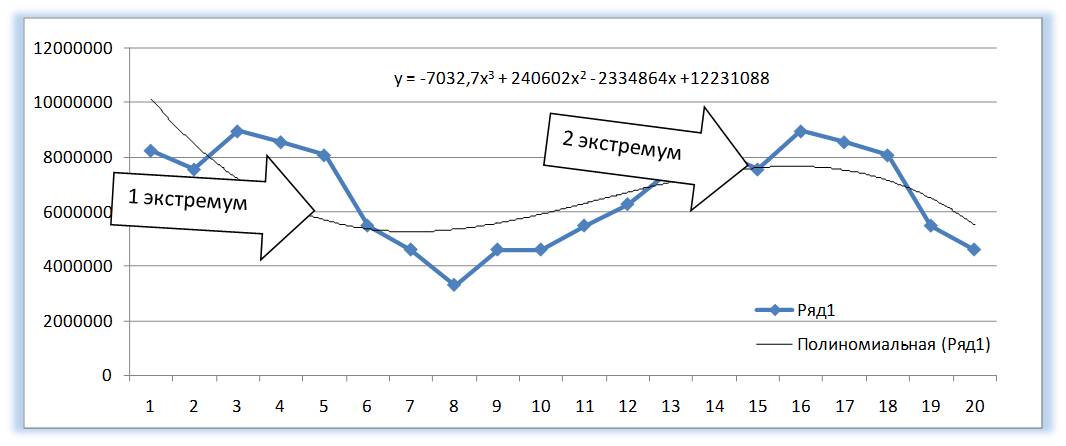
У Полинома третьей степени y=ax3+bx2+cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
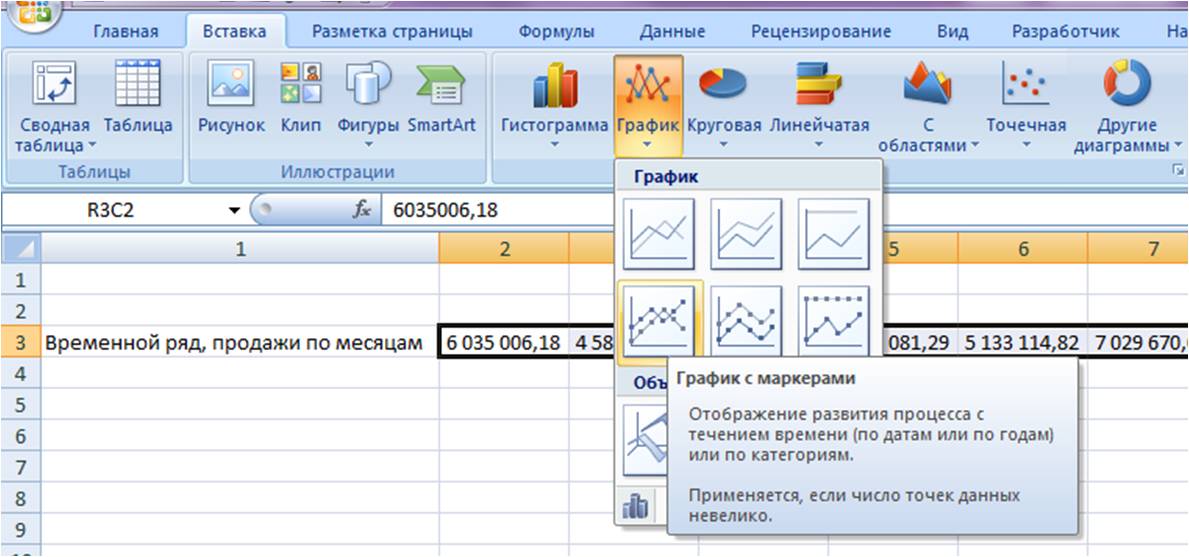
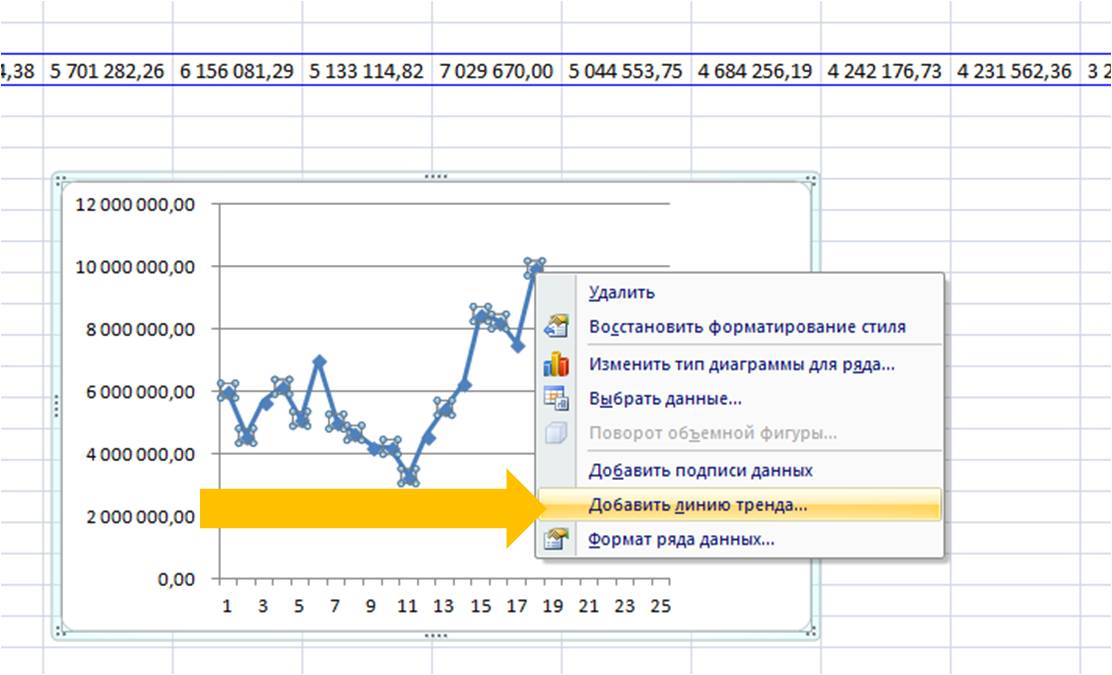
Выделяем ряд со значениями и строим график временного ряда.
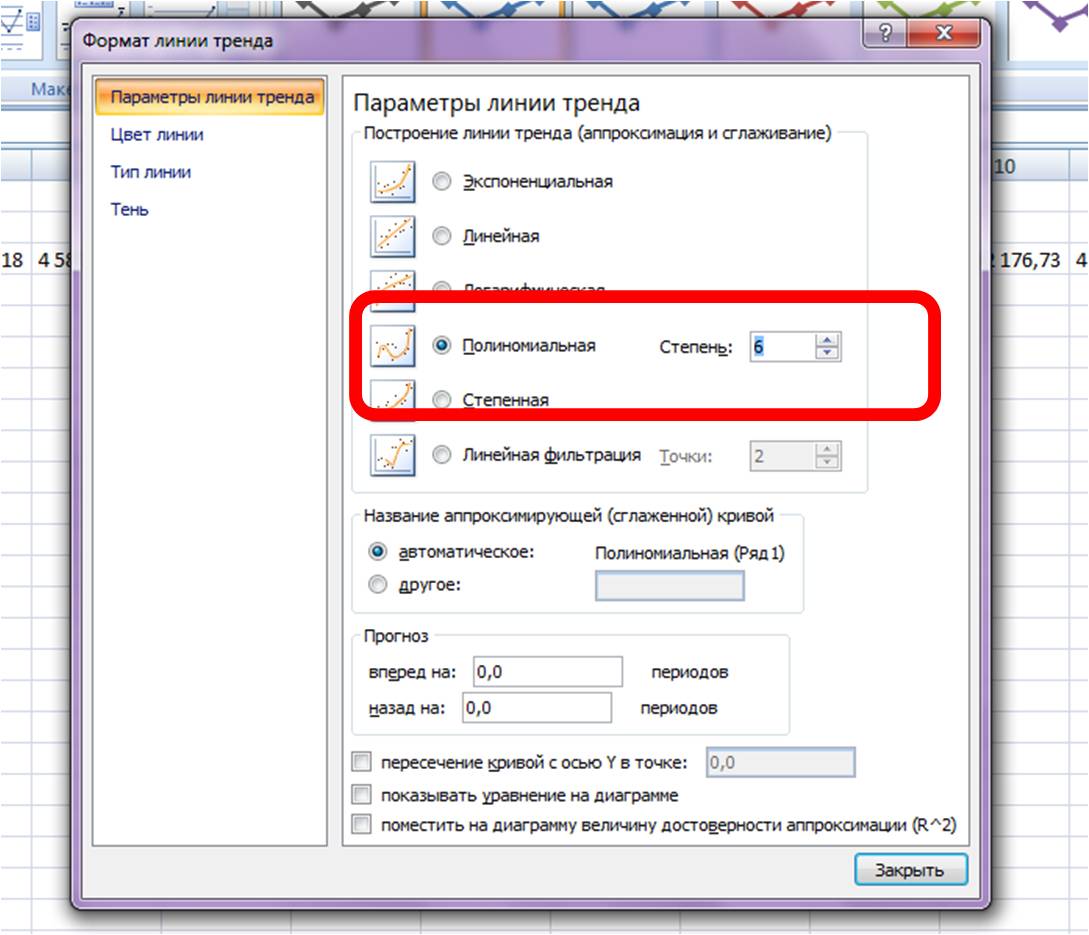
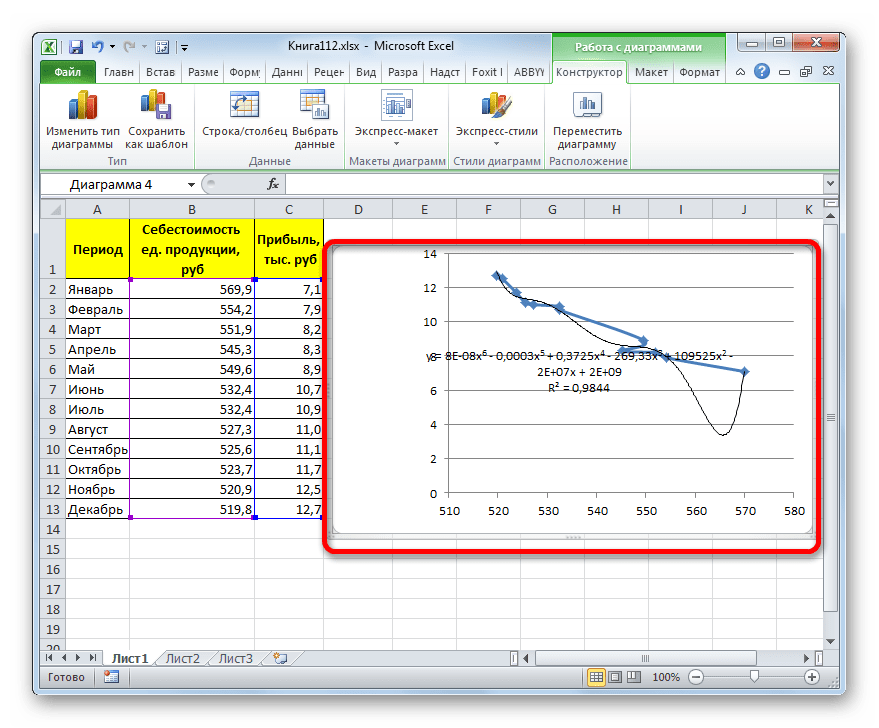
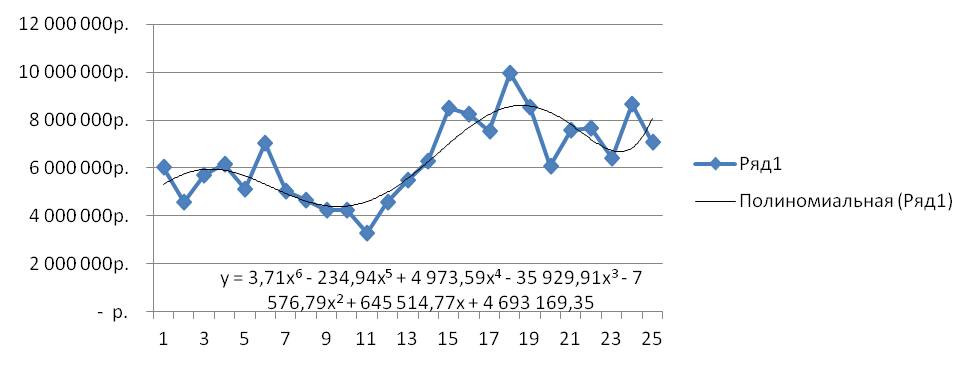
На график добавляем полином 6-й степени.
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
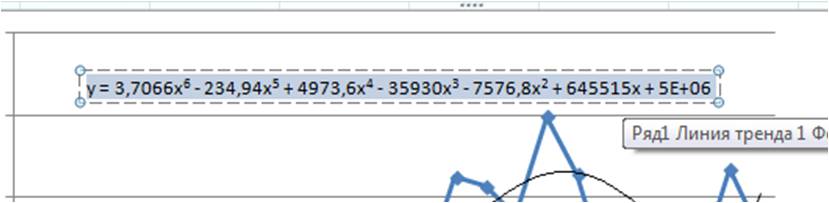
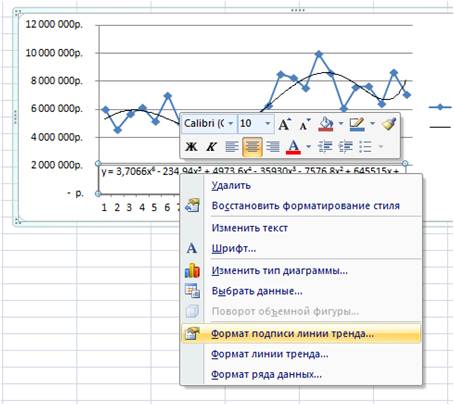
После этого уравнение выводится на график y = 3,7066x6 — 234,94x5 + 4973,6x4 — 35930x3 — 7576,8x2 + 645515x + 5E+06. Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
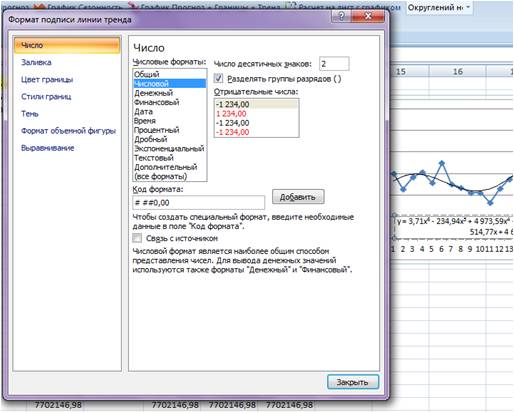
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35
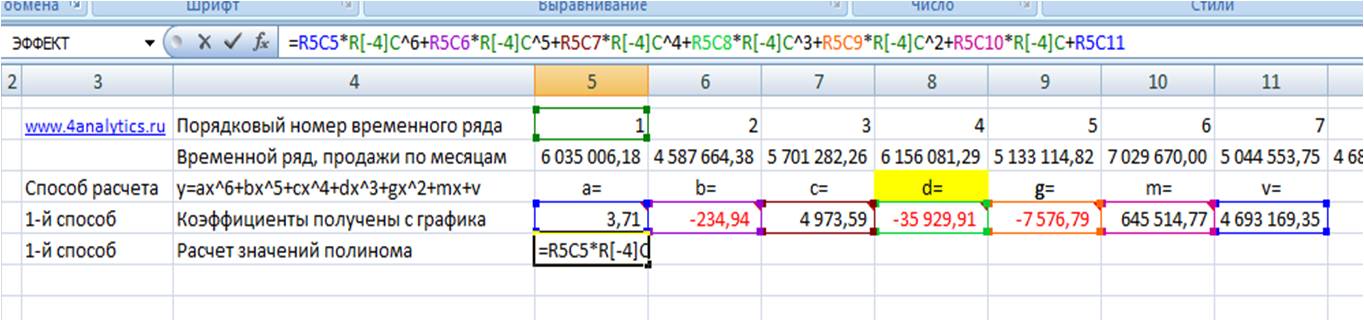
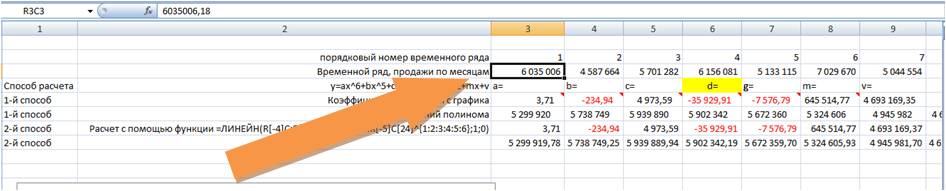
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
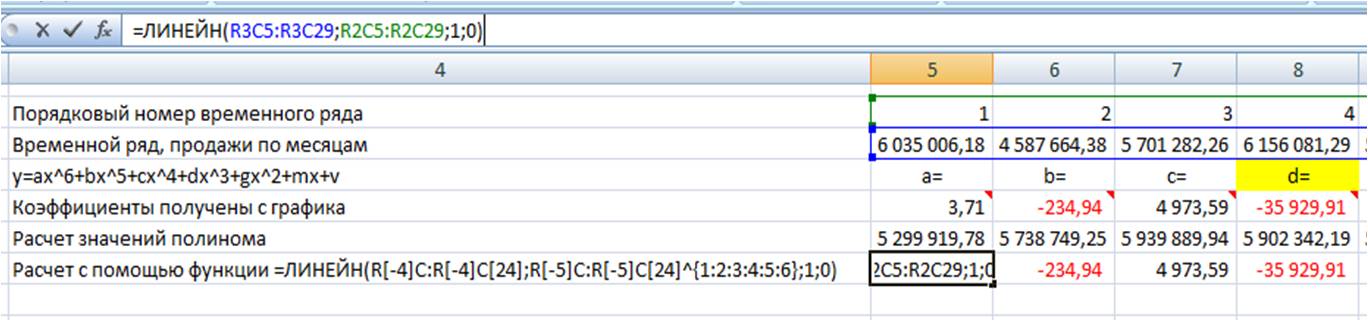
Получаем следующего вида формулу:
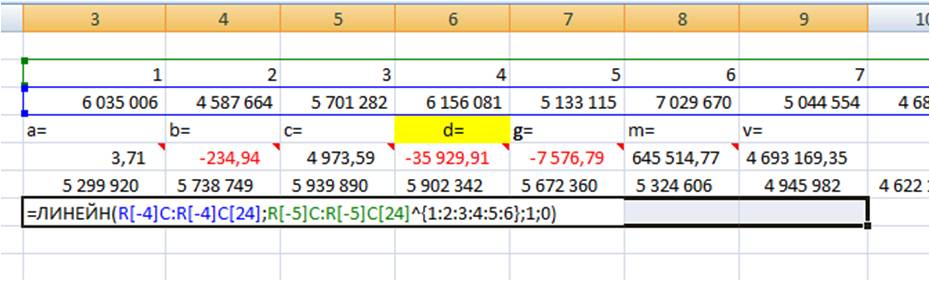
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^{1:2:3:4:5:6} — для расчета коэффициентов полинома 6-й степени
- ^{1:2:3:4:5} — для расчета коэффициентов полинома 5-й степени
- ^{1:2} — для расчета коэффициентов полинома 2-й степени
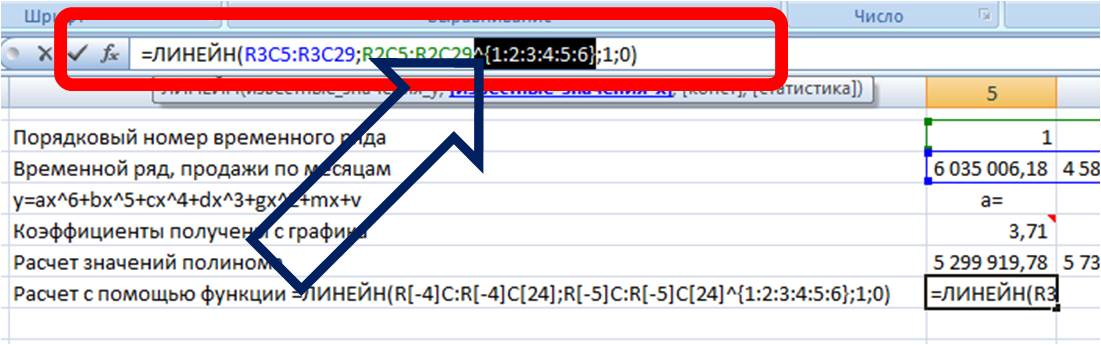
Получаем формулу следующего вида:
=ЛИНЕЙН(R[-4]C:R[-4]C[24]; R[-5]C:R[-5]C[24]^{1:2:3:4:5:6}; 1; 0)
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
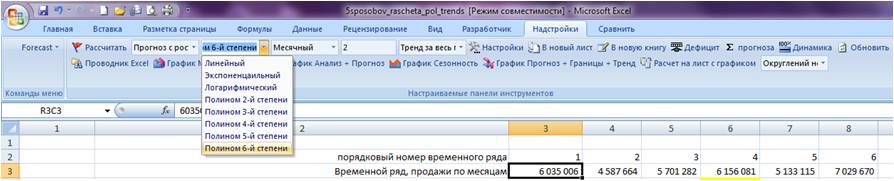
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
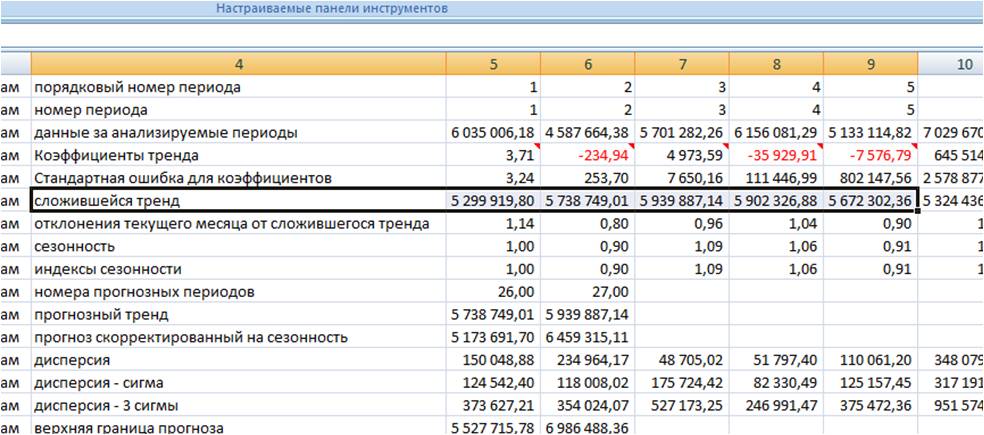
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
Скачать файл с примером расчета значений полинома.
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Содержание
- Как выполнить полиномиальную регрессию в Excel
- Пример: полиномиальная регрессия в Excel
- Excel построить полином по точкам
- Excel: как построить степенной полином функцией ЛИНЕЙН
- МНК: Приближение полиномом в EXCEL
- Как построить полиномиальную кривую в Excel (шаг за шагом)
- Шаг 1: Создайте данные
- Шаг 2: Подберите полиномиальную кривую
- Шаг 3: Интерпретация полиномиальной кривой
- Метод аппроксимации в Microsoft Excel
- Выполнение аппроксимации
- Способ 1: линейное сглаживание
- Способ 2: экспоненциальная аппроксимация
- Способ 3: логарифмическое сглаживание
- Способ 4: полиномиальное сглаживание
- Способ 5: степенное сглаживание
Как выполнить полиномиальную регрессию в Excel
Регрессионный анализ используется для количественной оценки взаимосвязи между одной или несколькими независимыми переменными и переменной отклика .
Наиболее распространенным типом регрессионного анализа является простая линейная регрессия , которая используется, когда независимая переменная и переменная отклика имеют линейную связь.
Однако иногда связь между объясняющей переменной и переменной отклика нелинейна.
В этих случаях имеет смысл использовать полиномиальную регрессию , которая может учитывать нелинейную связь между переменными.
В этом руководстве объясняется, как выполнить полиномиальную регрессию в Excel.
Пример: полиномиальная регрессия в Excel
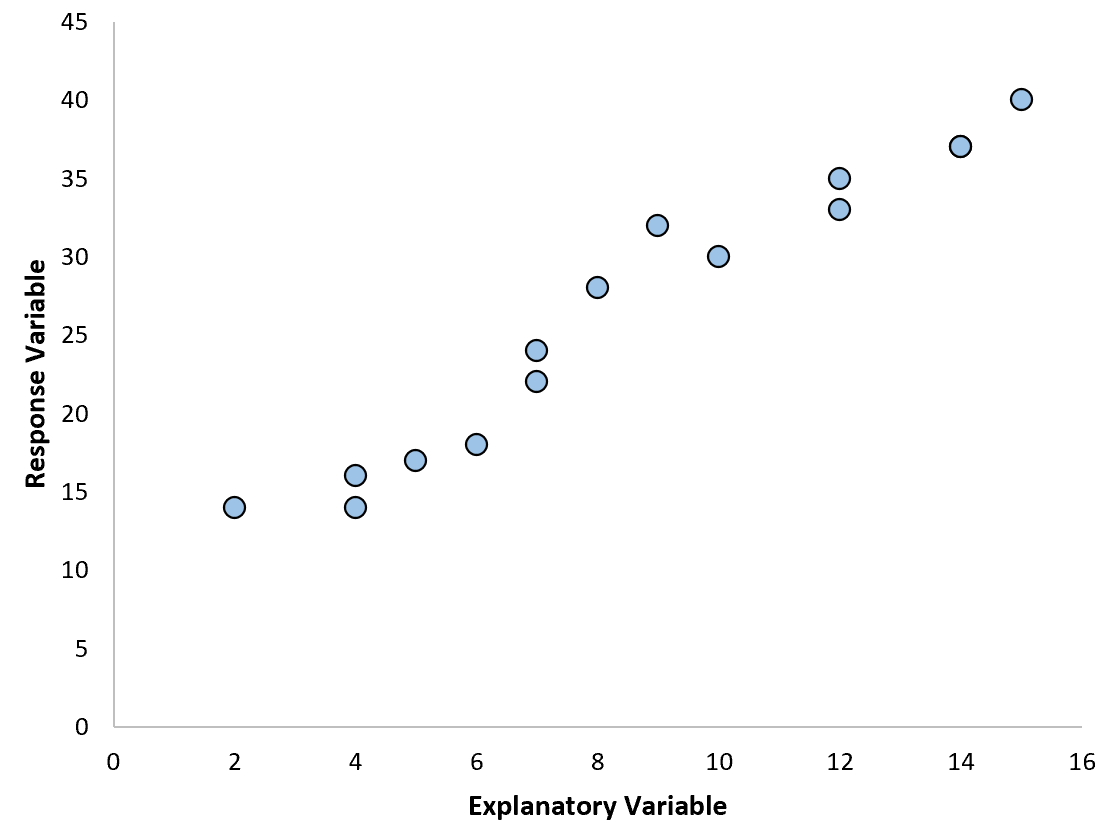
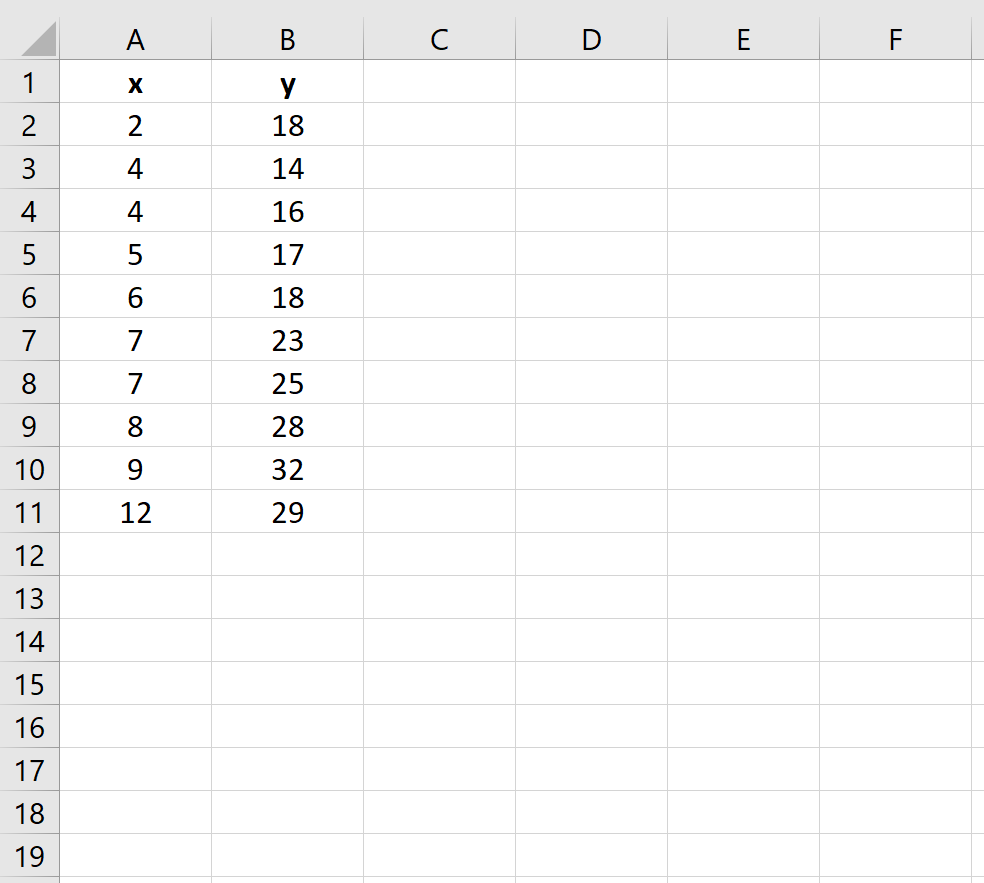
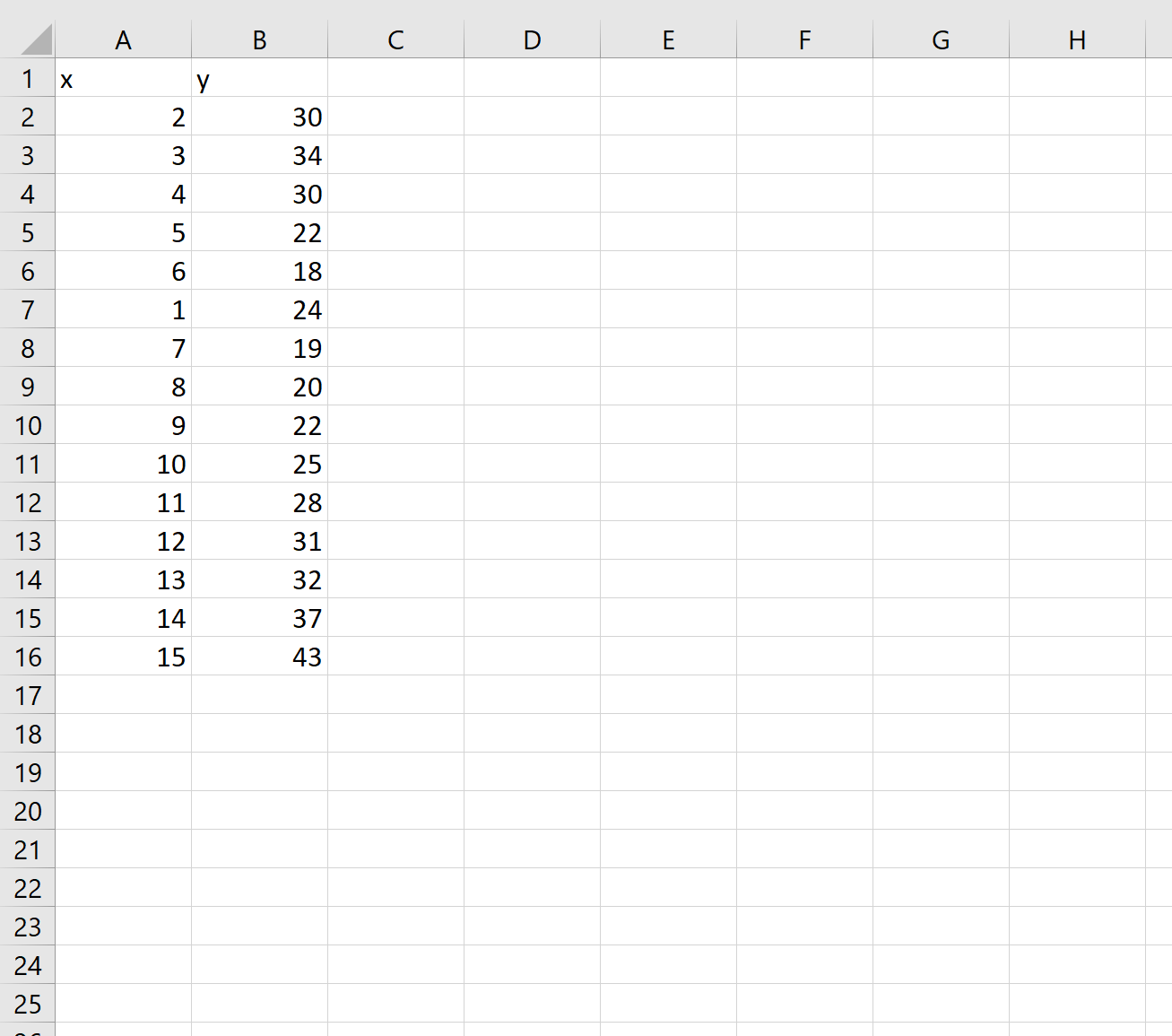
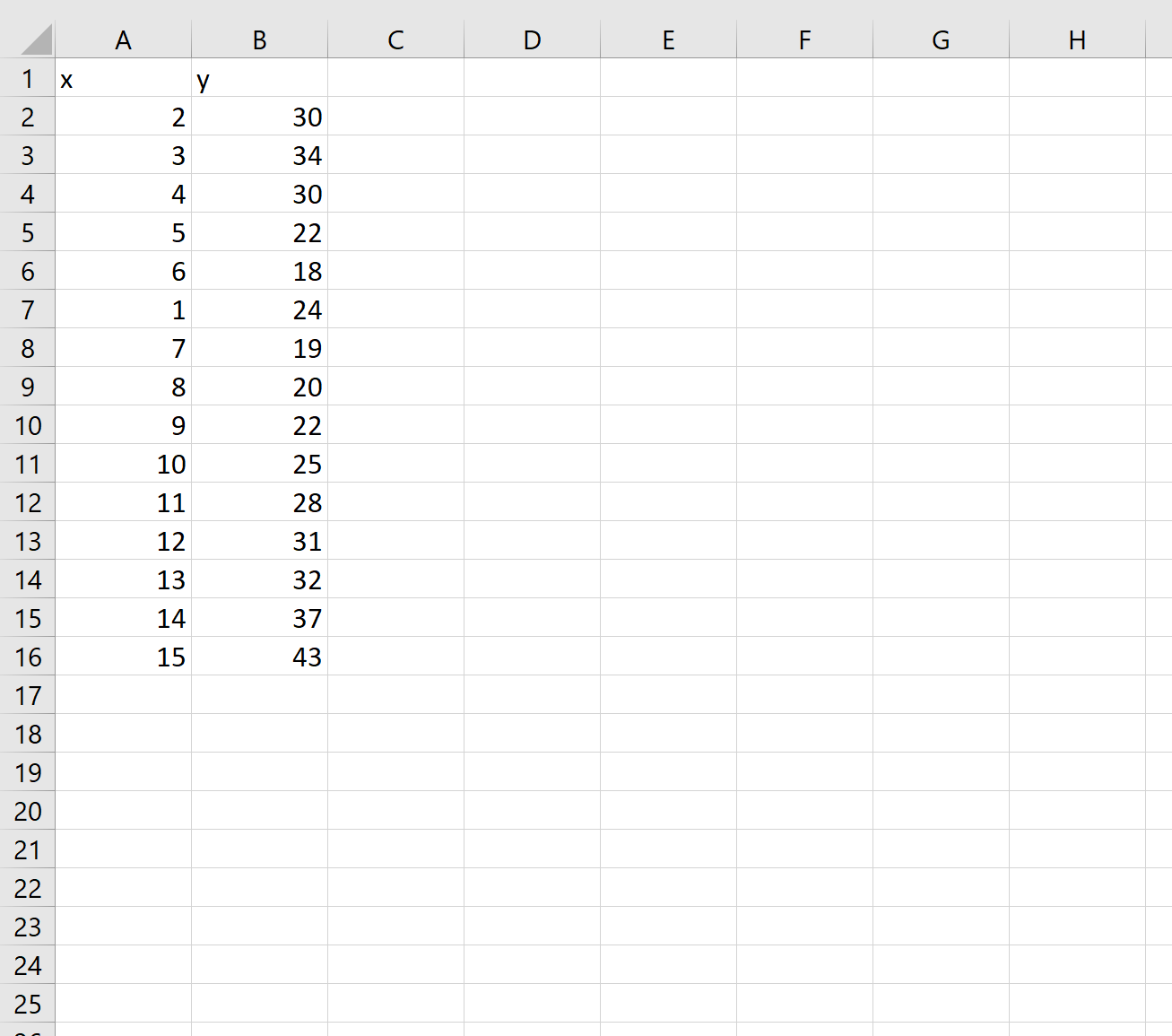
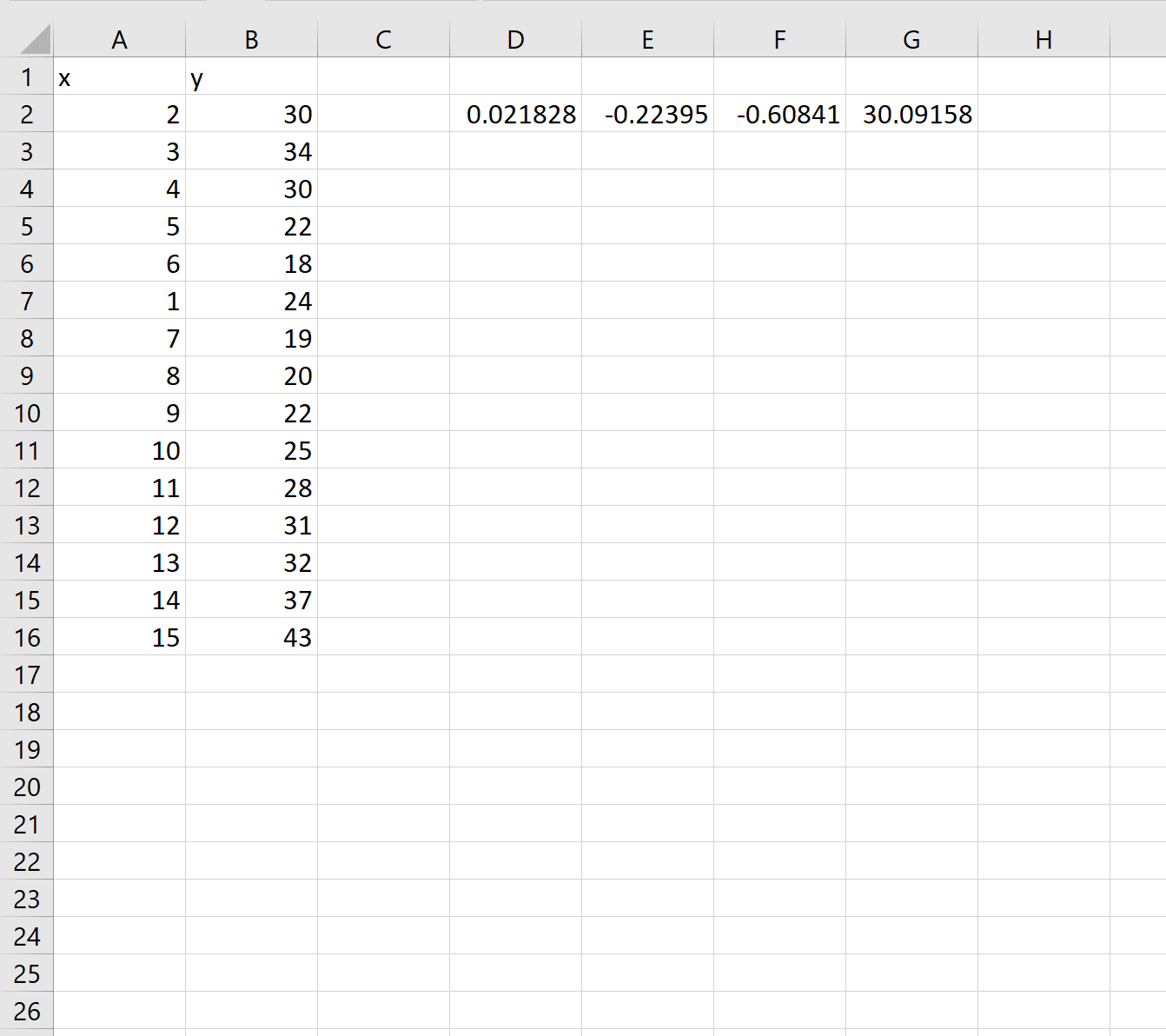
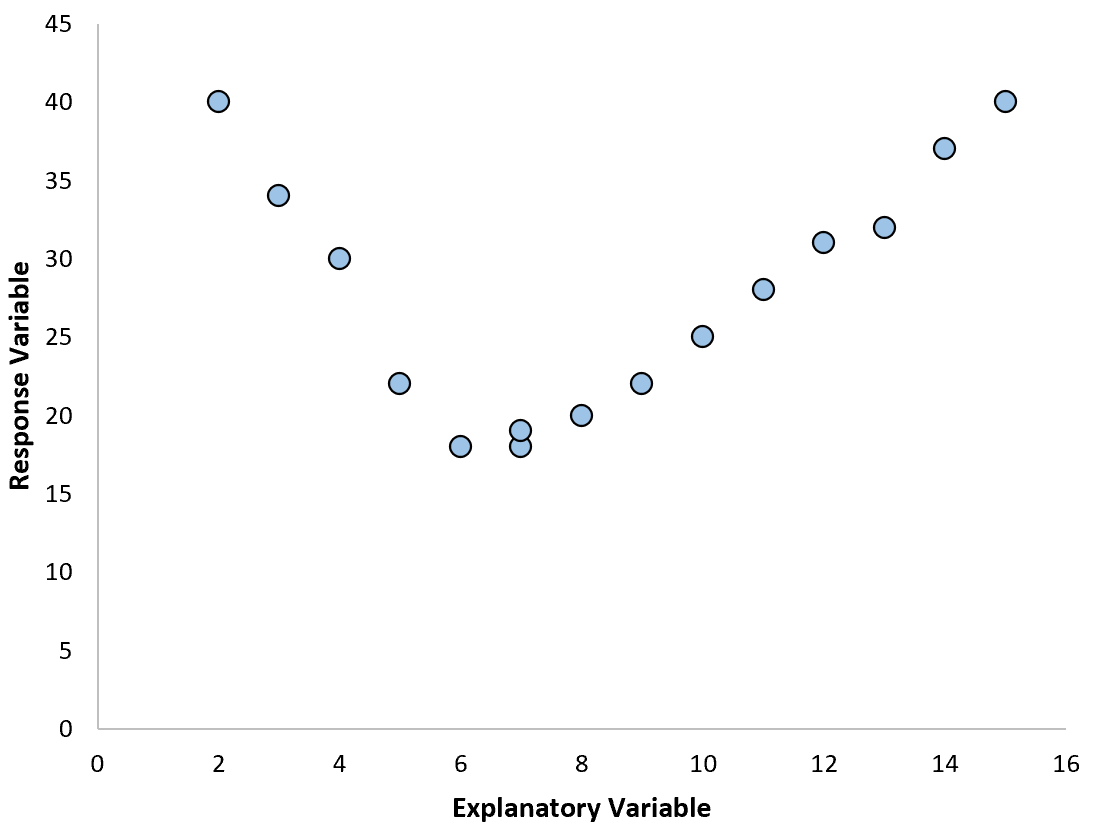
Предположим, у нас есть следующий набор данных в Excel:
Используйте следующие шаги, чтобы подогнать уравнение полиномиальной регрессии к этому набору данных:
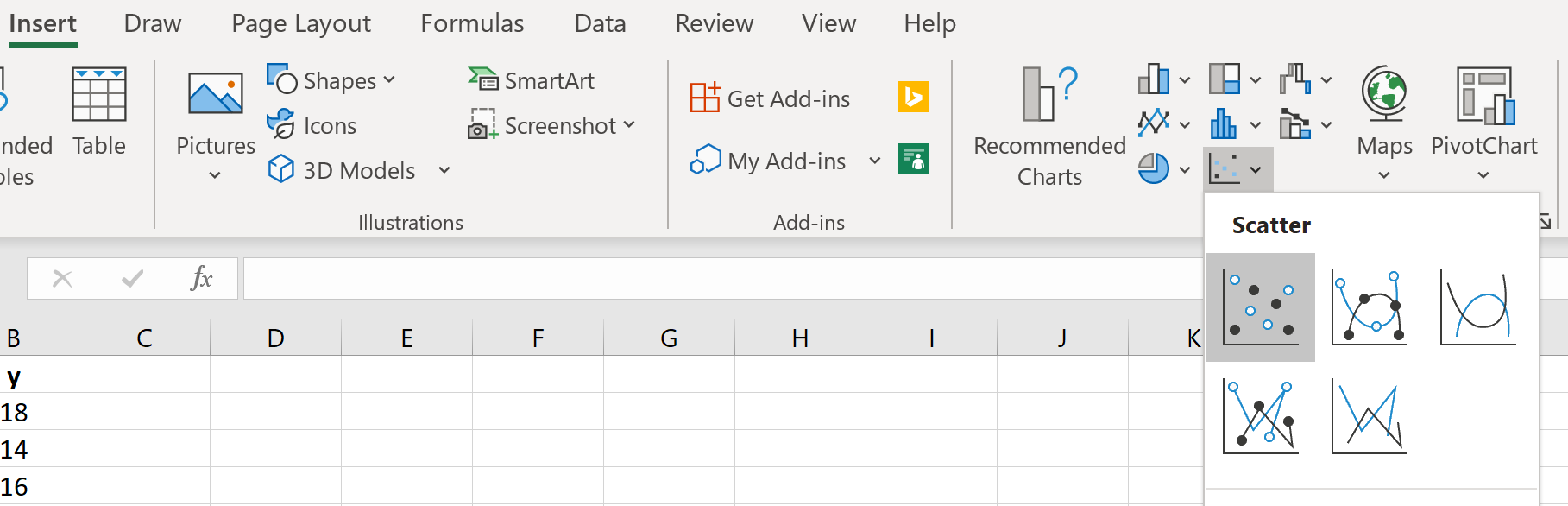
Шаг 1: Создайте диаграмму рассеяния.
Во-первых, нам нужно создать диаграмму рассеяния. Перейдите в группу Charts на вкладке Insert и щелкните первый тип диаграммы в Scatter :
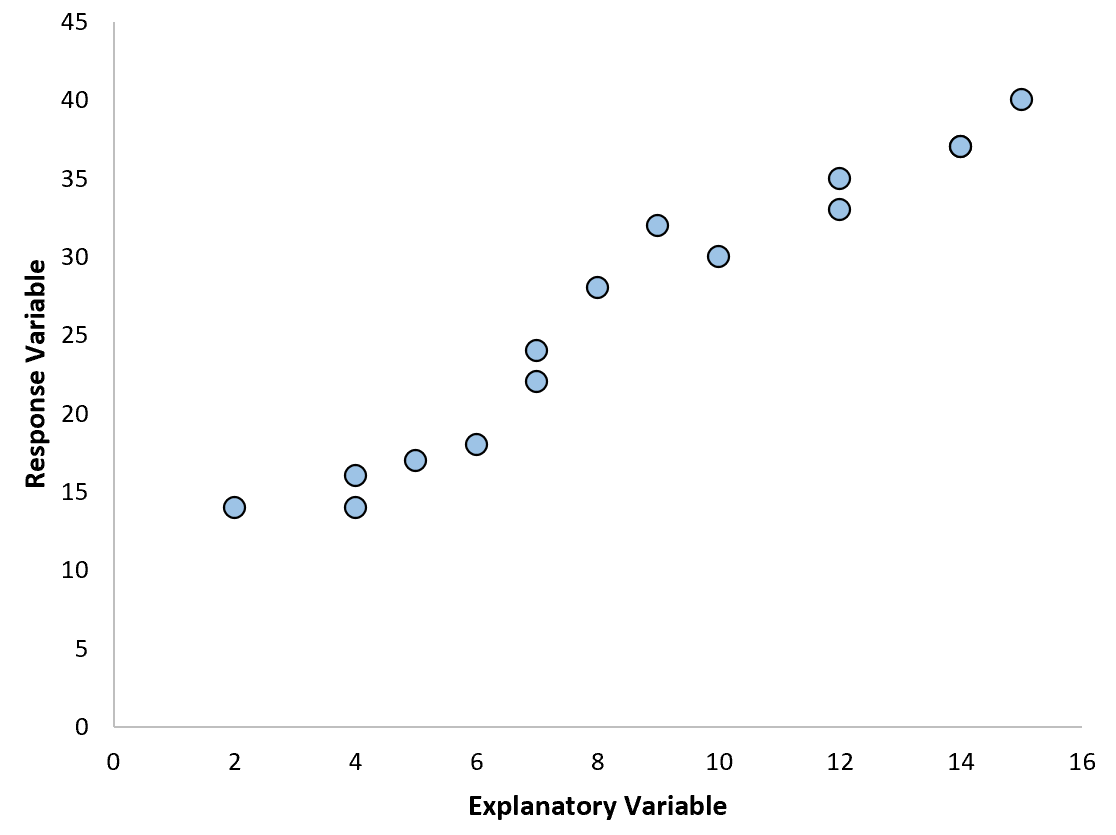
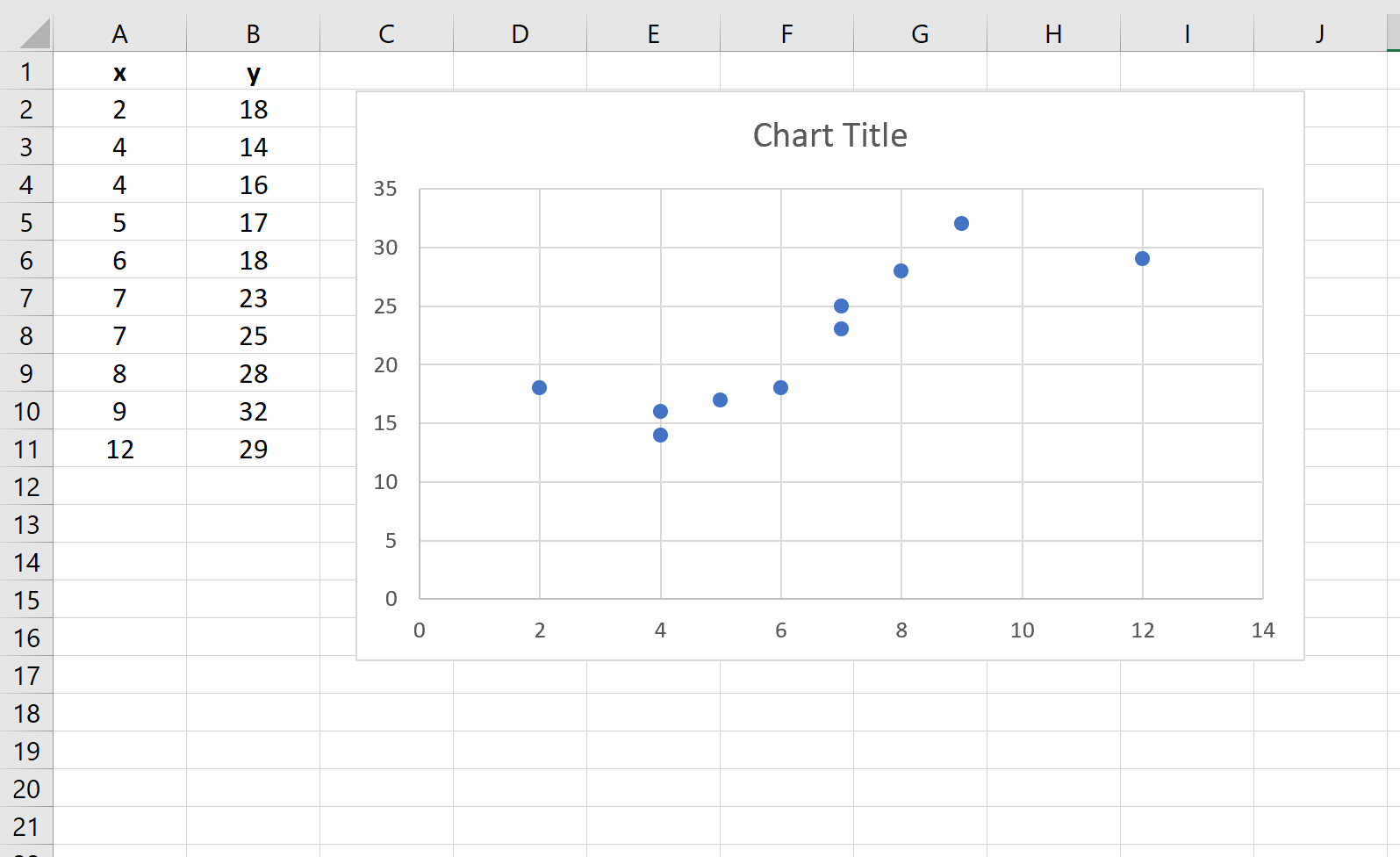
Автоматически появится диаграмма рассеяния:
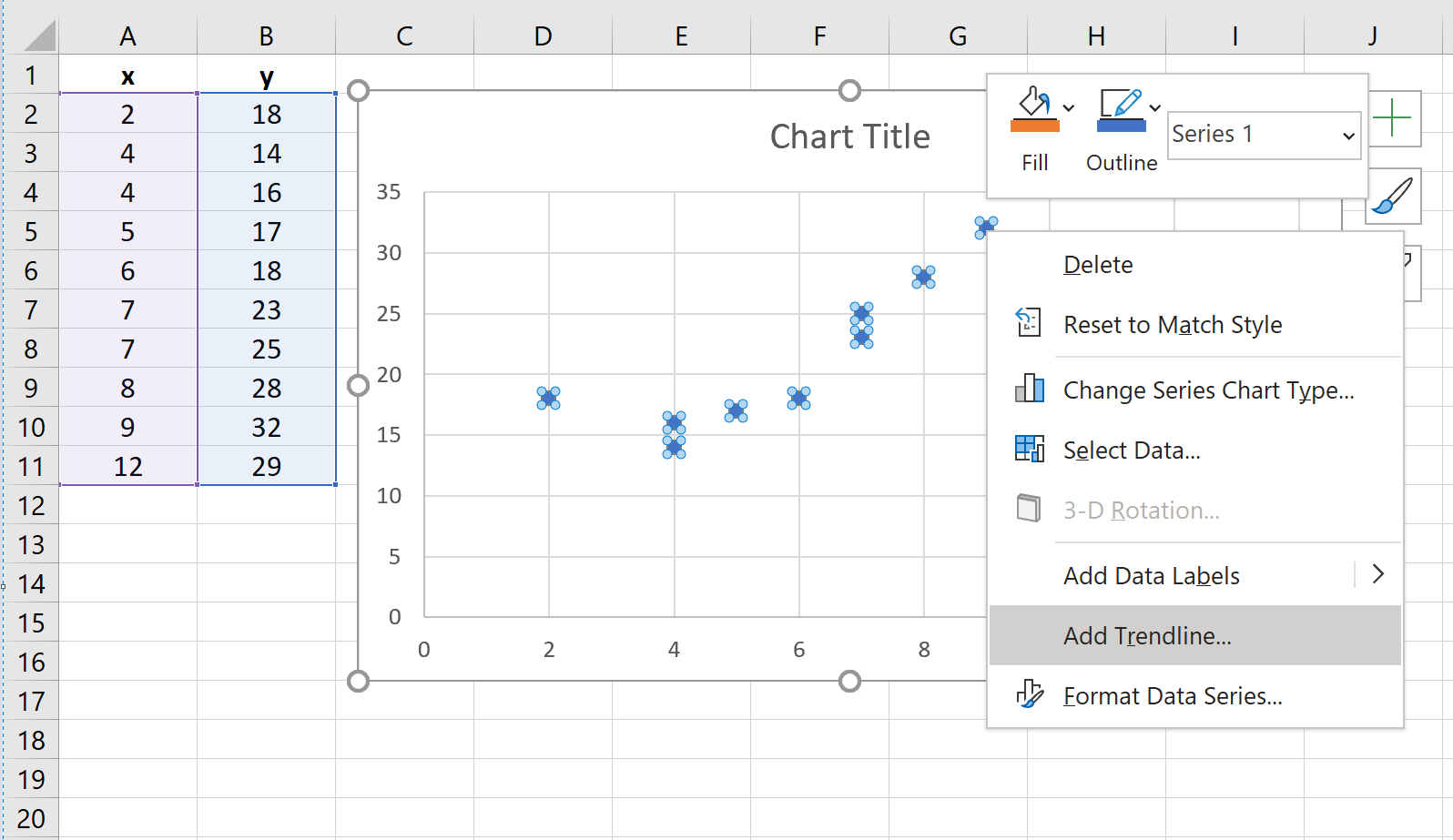
Шаг 2: Добавьте линию тренда.
Далее нам нужно добавить линию тренда на диаграмму рассеяния. Для этого щелкните любую из отдельных точек на диаграмме рассеивания. Затем щелкните правой кнопкой мыши и выберите «Добавить линию тренда…».
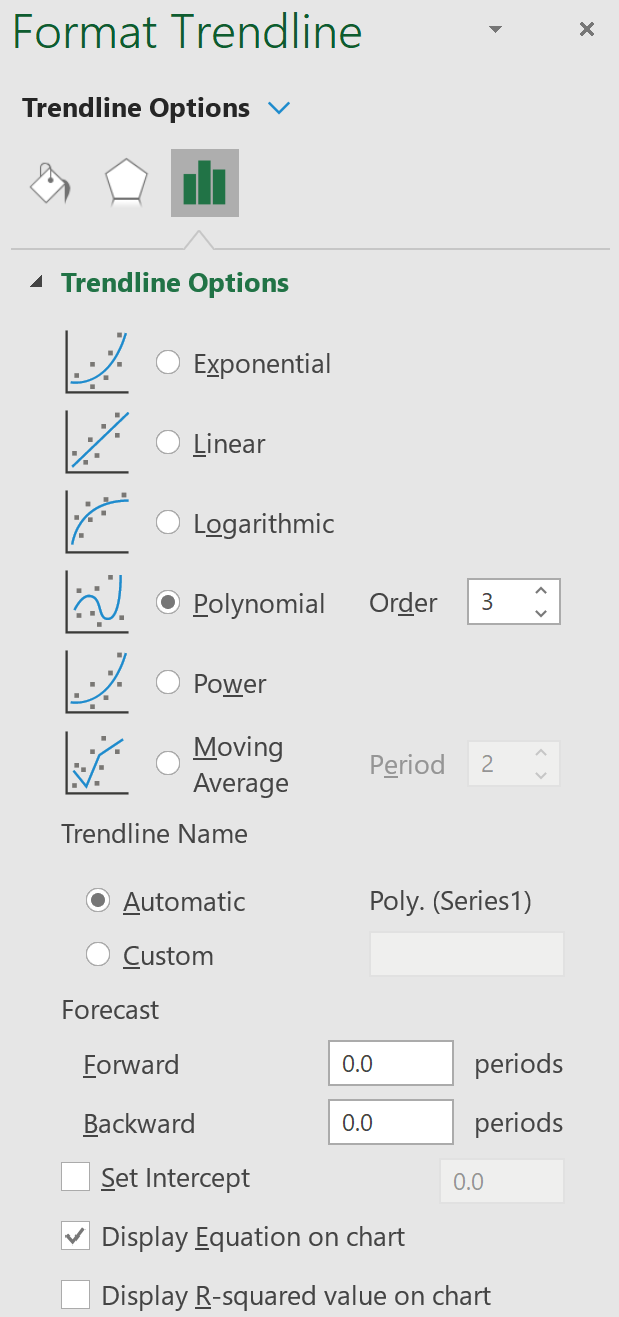
Появится новое окно с возможностью указать линию тренда. Выберите Polynomial и выберите число, которое вы хотите использовать для Order.Мы будем использовать 3. Затем установите флажок рядом с надписью Display Equation on chart внизу.
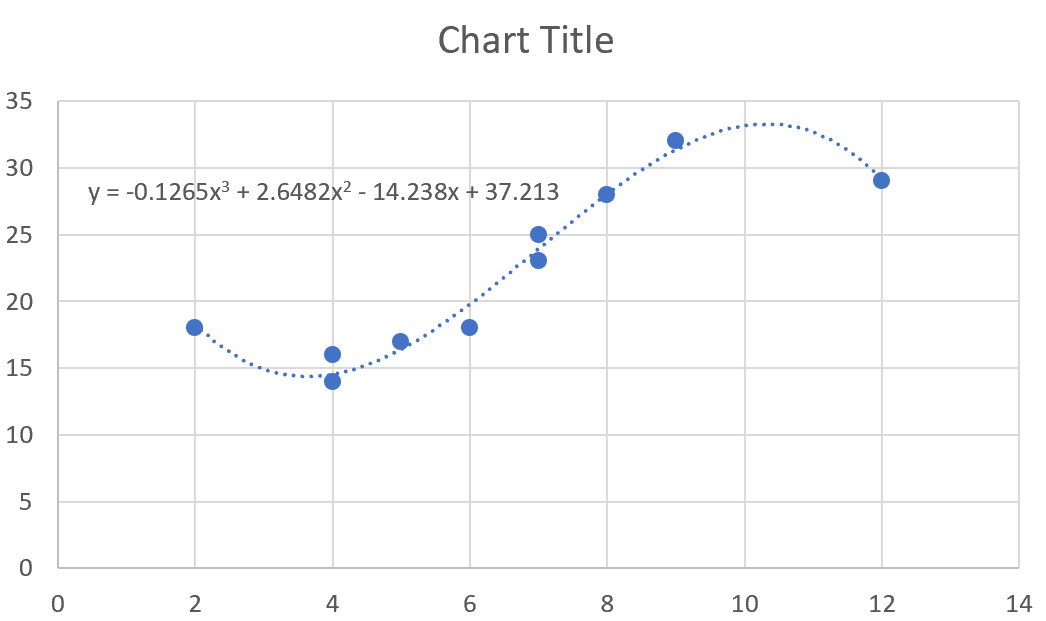
На диаграмме рассеяния автоматически появится линия тренда с уравнением полиномиальной регрессии:
Шаг 3: Интерпретируйте уравнение регрессии.
Для этого конкретного примера наше подобранное уравнение полиномиальной регрессии:
у = -0,1265 х 3 + 2,6482 х 2 – 14,238 х + 37,213
Это уравнение можно использовать для нахождения ожидаемого значения переменной отклика на основе заданного значения объясняющей переменной. Например, предположим, что x = 4. Ожидаемое значение переменной ответа y будет следующим:
у = -0,1265(4) 3 + 2,6482(4) 2 – 14,238(4) + 37,213 = 14,5362 .
Источник
Excel построить полином по точкам
БлогNot. Excel: как построить степенной полином функцией ЛИНЕЙН
Excel: как построить степенной полином функцией ЛИНЕЙН
Сейчас мы хотим, во-первых, построить в Excel интерполирующий полином тоже стандартной функцией, во-вторых, не вдаваясь в детали теории, понять смысл этой простой задачи — как построить кривую, проходящую через несколько известных точек на плоскости.
Итак, по известному набору из N значений функции f(xi)=yi , заданному парой векторов xi, yi=f(xi) , i=1, 2, . N , нужно построить кривую, проходящую через все точки.
Через N различных между собой по оси x точек всегда можно построить кривую, зависящую от x N-1 , её уравнение будет иметь общий вид
В этом уравнении нам неизвестны коэффициенты сi . Из условия, что кривая проходит через все заданные в постановке задачи точки, можно записать систему линейных алгебраических уравнений:
или, в матричном виде
Решив эту систему уравнений, то есть, найдя обратную к матрице Вандермонда матрицу и умножив её на вектор y , найдём коэффициенты сi . Теперь, подставив их в уравнение (1), мы можем аналитически оценить значение функции в произвольной точке x .
Ниже показано «ручное» решение в Excel и решение с помощью стандартной функции ЛИНЕЙН.
Вот пояснения к формулам:
- C2 — формируем матрицу из степеней значений x ; избегаем при этом возведения нуля в нулевую степень, заменяя любое число, возводимое в нулевую степень, единицей; ввести формулу в ячейку C2 ; затем растягиваем формулу на ячейки C2:C5 , отпускаем левую кнопку мыши и, не снимая выделения, растягиваем на столбцы D:F (см. Пояснение 1 ниже);
- G2:G5 — вычисляем коэффициенты полинома ci «вручную», обратив матрицу и умножив её на вектор значений yi ; выделить диапазон G2:G5 ; не снимая выделения, ввести формулу в ячейку G2 ; не снимая выделения, нажать комбинацию клавиш Crl+Shift+Enter (см. Пояснение 2 ниже);
- I2 — вычисляем полином третьей степени в точках, не обязательно совпадающих с исходными; по выделенным жирным шрифтом значениям полинома видно, что он прошёл через исходные точки; ввести формулу в ячейку I2 , растянуть за уголок до I8 ;
- J2:J5 — вычисляем коэффициенты полинома ci с помощью функции ЛИНЕЙН , пример в справке (пример 2), к сожалению, прямо ошибочен, плюс не показывает вычисление нескольких коэффициентов полинома; выделить диапазон J2:J5 ; не снимая выделения, ввести формулу в ячейку G2 ; не снимая выделения, нажать комбинацию клавиш Crl+Shift+Enter ; коэффициенты возвращаются в «перевёрнутом» по отношению к нашему ручному расчёту виде;
- K2 — для единообразия расчёта переворачиваем массив коэффициентов, готовой функции для этого нет, показан образец, как перевернуть диапазон в Excel; ввести формулу в ячейку K2 , растянуть за уголок до K5 ;
- L2 — вычисляем полином третьей степени в тех же точках H2:H8 , в которых вычисляли его значения первым способом; ввести формулу в ячейку L2 , растянуть за уголок до L8 ; видно, что кривая также прошла через исходные точки данных.

Пояснение 1. Как растянуть формулу на матрицу значений
1. Введите требуемую формулу и нажмите Enter , на рисунке показан вид экрана перед нажатием:
2. Подведите курсор мыши к нижнему правому уголку ячейки C2 , уголок превратился в чёрный крестик, зажмите левую кнопку мыши и растяните формулу вниз до ячейки C5 .
3. Отпустите кнопку мыши, снова так же подведите курсор к уголку ячейки C5 (опять чёрный крестик) и при зажатой левой кнопке мыши растяните выделение вправо до столбца F .
Пояснение 2. Как ввести формулу массива
1. Выделить диапазон ячеек, в которые будет помещён результат матричной или векторной операции (мышкой при зажатой левой кнопке за любое место, на котором курсор имеет вид по умолчанию или при зажатой Shift клавишами со стрелками):
Мы сами отвечаем за правильность выделения ячеек диапазона результата, например, Excel не обязан знать, что в результате обращения матрицы размерностью 3×3 получится тоже матрица размерностью 3×3 :
2. Не снимая выделения, ввести формулу массива в первую ячейку выделенного диапазона, это можно сделать «вручную», просто нажав клавишу F2 и начав набирать формулу со знака » = «, или с помощью Мастера Функций (см. п.3 документа по Excel здесь).
3. При зажатых клавишах Ctrl и Shift , нажать клавишу Enter , то есть, ввести комбинацию клавиш Ctrl+Shift+Enter .
Источник
МНК: Приближение полиномом в EXCEL
history 24 ноября 2018 г.
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).
В основной статье про МНК было рассмотрено приближение линейной функцией. В этой статье рассмотрим приближение полиномиальной функцией (с 3-й до 6-й степени) следующего вида: y=b 0 +b 1 x+b 2 x 2 +b 3 x 3 +…+b 6 x 6
Примечание : В инструменте MS EXCEL Линия тренда , который доступен для диаграмм типа Точечная и График , можно построить линию тренда на основе полинома с максимальной степенью 6. В файле примера продемонстрировано полное совпадение линии тренда диаграммы и линии, вычисленной с помощью формул.
Покажем, как вычислить коэффициенты b линии тренда, заданной полиномом.
Как известно, квадратичная зависимость y=b 0 +b 1 x+b 2 x 2 , подробно рассмотренная в статье МНК: Квадратичная зависимость в MS EXCEL , является частным случаем полиномиальной y=b 0 +b 1 x+b 2 x 2 +b 3 x 3 +… зависимости (в этом случае степень полинома равна 2). Соответственно, используя тот же подход (приравнивание к 0 частных производных), можно вычислить коэффициенты любого полинома.
Примечание : Существует еще один метод вычисления коэффициентов – замена переменных, который рассмотрен в конце статьи.
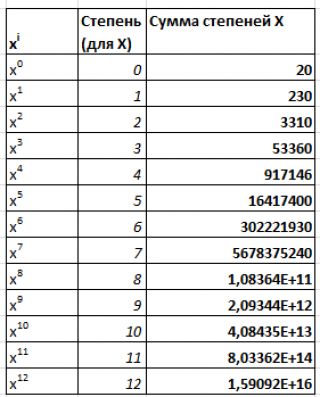
Для нахождения m+1 коэффициента полинома m-й степени составим систему из m+1 уравнения и решим ее методом обратной матрицы . Для квадратного уравнения (m=2) нам потребовалось вычислить сумму значений х с 1-й до 4-й степени, а для полинома m-й степени необходимо вычислить значения х с 1-й до 2*m степени.
Примечание : Для удобства суммы степеней значений х можно вычислить в отдельном диапазоне ( файл примера столбцы К:М).
В файле примера создана универсальная форма для вычисления коэффициентов полиномов.
Выбрав с помощью элемента управления Счетчик нужную степень полинома, автоматически получим аппроксимацию наших данных выбранным полиномом (будет построен соответствующий график).
Примечание: При использовании полиномов высокой степени необходимо следить за тем, чтобы количество пар значений (х i ; y i ) превышало степень полинома хотя бы на несколько значений (для обеспечения точности аппроксимации). Кроме того, график функции полинома степени m имеет m-1 точку перегиба. Понятно, что точек данных должно быть гораздо больше, чем точек перегиба, чтобы такой изменчивый тренд стал очевидным (если утрировать, то бессмысленно строить по двум точкам параболу, логичнее построить прямую).
Как видно из расчетов, в MS EXCEL этот путь является достаточно трудоемким. Гораздо проще в MS EXCEL реализовать другой подход для вычисления коэффициентов полинома — с помощью замены переменных.
С помощью замены переменных x i =x i полиномиальную зависимость y=b 0 +b 1 x+b 2 x 2 +b 3 x 3 +… можно свести к линейной. Теперь переменная y зависит не от одной переменной х в m разных степенях, а от m независимых переменных x i . Поэтому для нахождения коэффициентов полинома мы можем использовать функцию ЛИНЕЙН() . Этот подход также продемонстрирован в файле примера .
Источник
Как построить полиномиальную кривую в Excel (шаг за шагом)
Вы можете использовать функцию ЛИНЕЙН() в Excel, чтобы подобрать полиномиальную кривую с определенной степенью.
Например, вы можете использовать следующий базовый синтаксис, чтобы подогнать полиномиальную кривую со степенью 3:
Функция возвращает массив коэффициентов, описывающих полиномиальную подгонку.
В следующем пошаговом примере показано, как использовать эту функцию для подбора полиномиальной кривой в Excel.
Шаг 1: Создайте данные
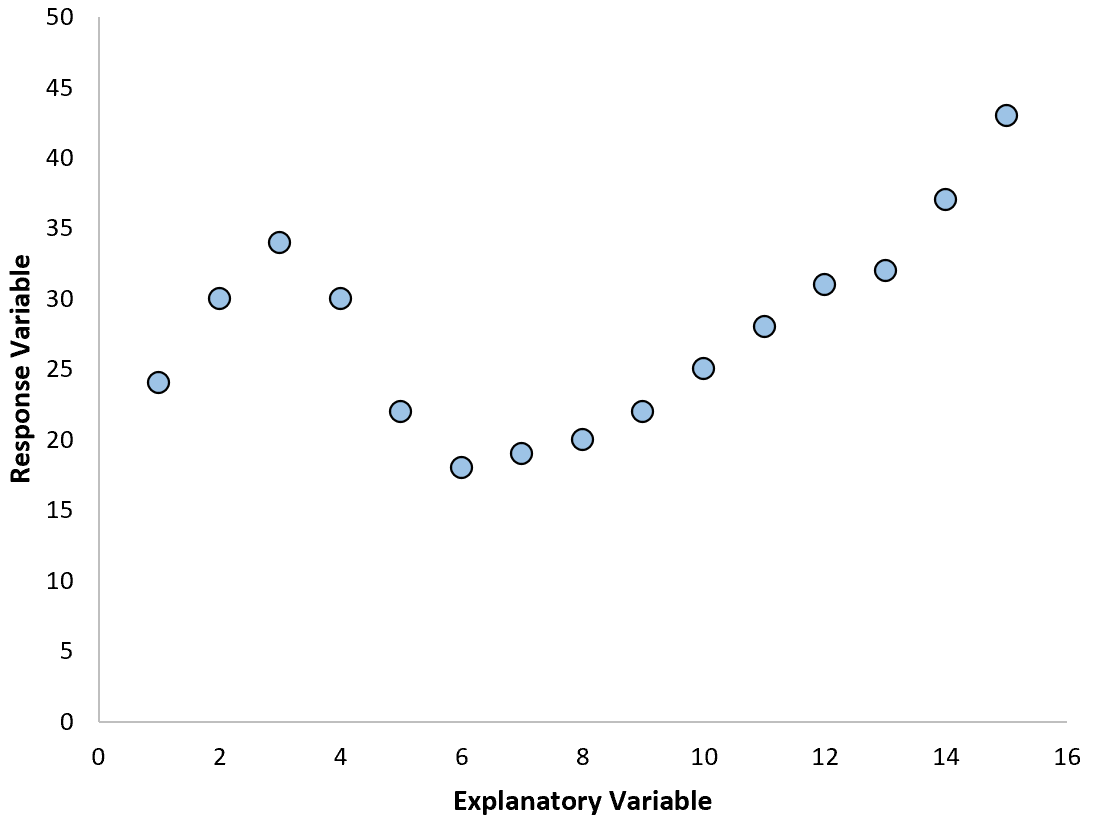
Во-первых, давайте создадим некоторые данные для работы:
Шаг 2: Подберите полиномиальную кривую
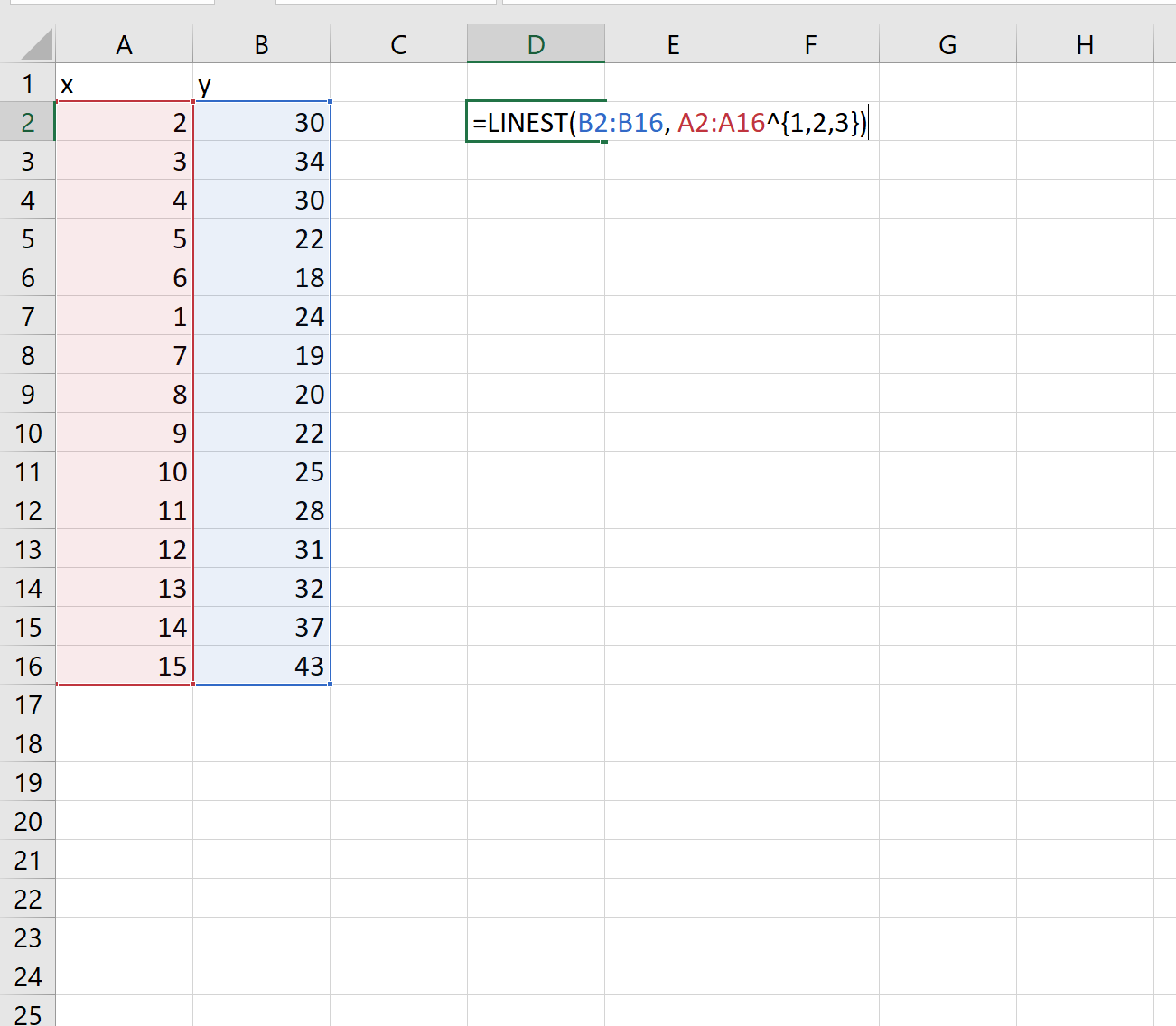
Далее воспользуемся функцией ЛИНЕЙН() , чтобы подобрать полиномиальную кривую степени 3 к набору данных:
Шаг 3: Интерпретация полиномиальной кривой
Как только мы нажмем ENTER , появится массив коэффициентов:
Используя эти коэффициенты, мы можем построить следующее уравнение, описывающее взаимосвязь между x и y:
у = 0,0218x 3 – 0,2239x 2 – 0,6084x + 30,0915
Мы также можем использовать это уравнение для вычисления ожидаемого значения y на основе значения x.
Например, предположим, что x = 4. Ожидаемое значение y будет следующим:
у = 0,0218(4) 3 – 0,2239(4) 2 – 0,6084(4) + 30,0915 = 25,47
Источник
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
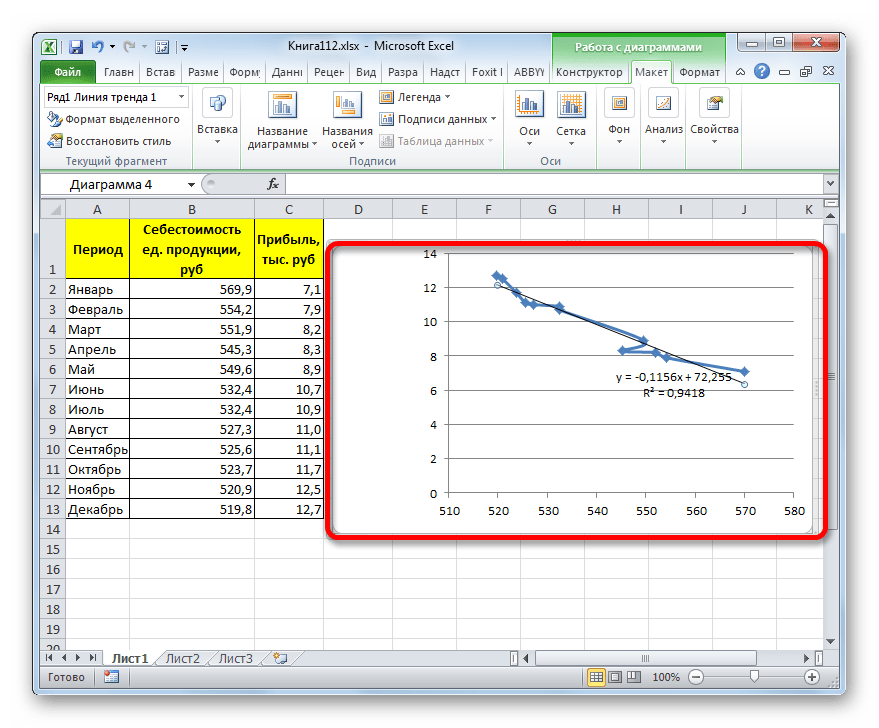
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
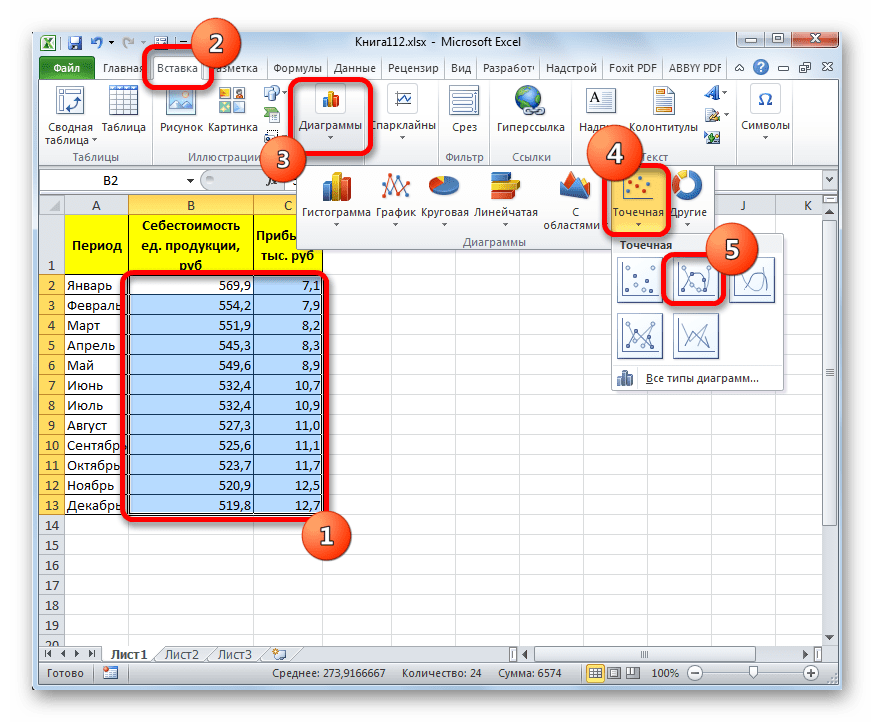
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
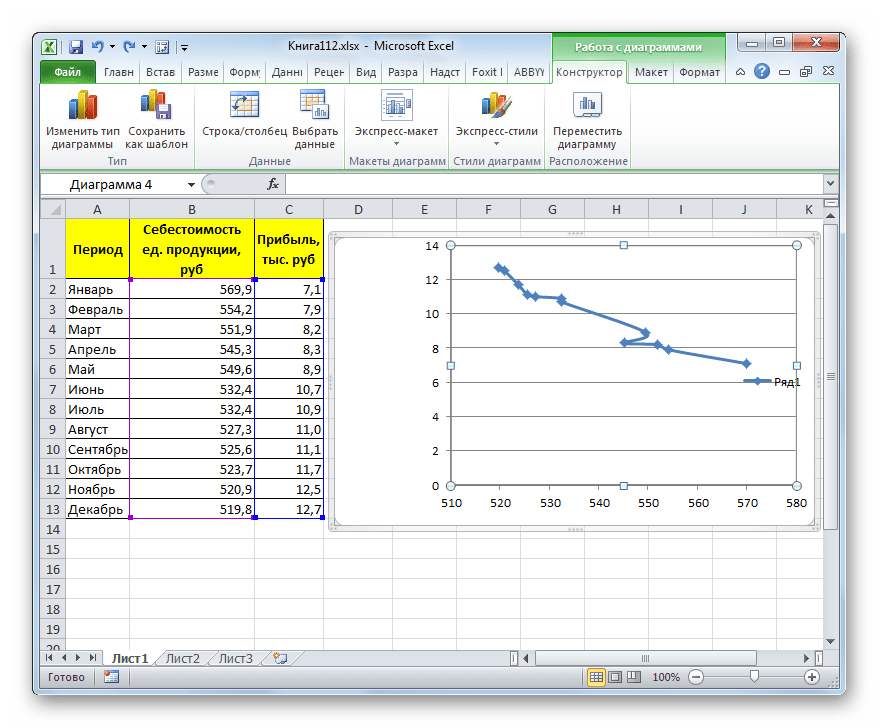
- График построен.
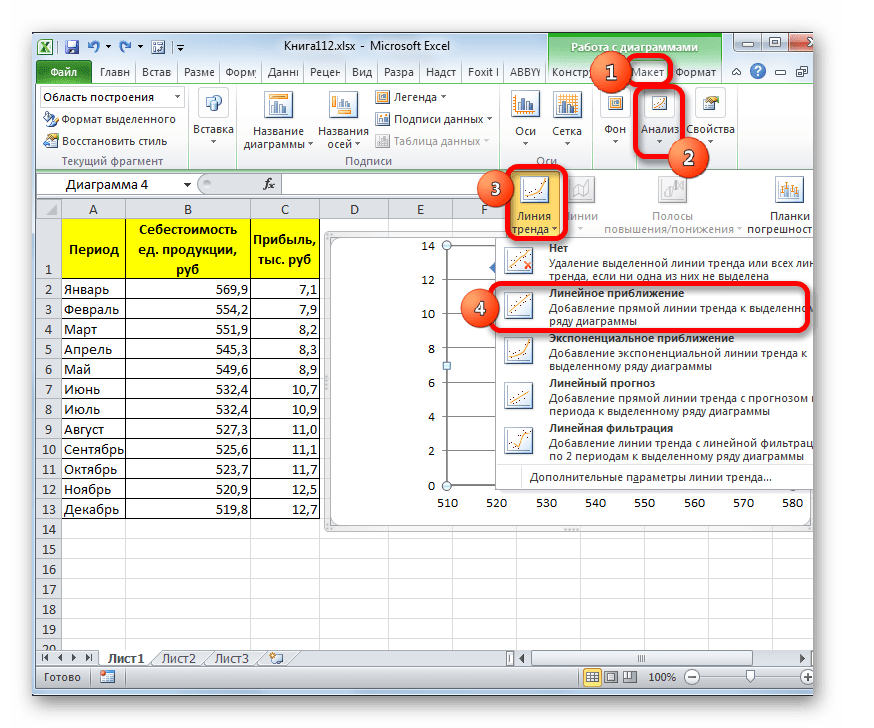
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна. 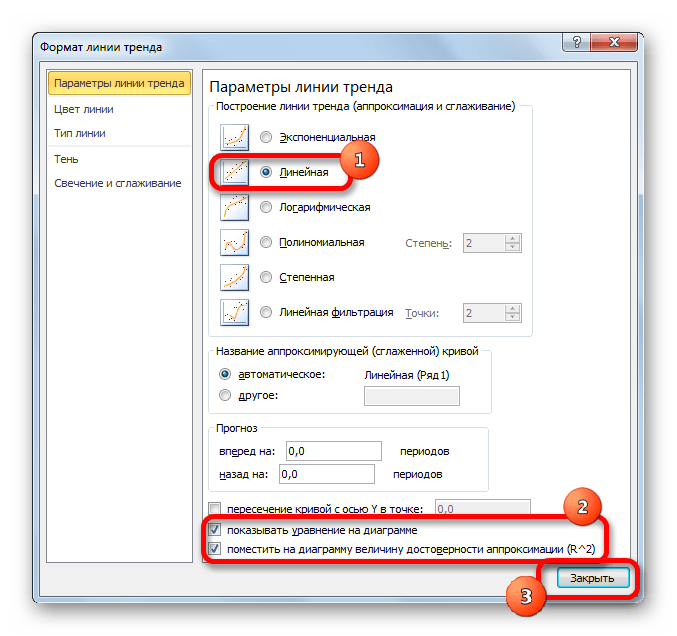
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
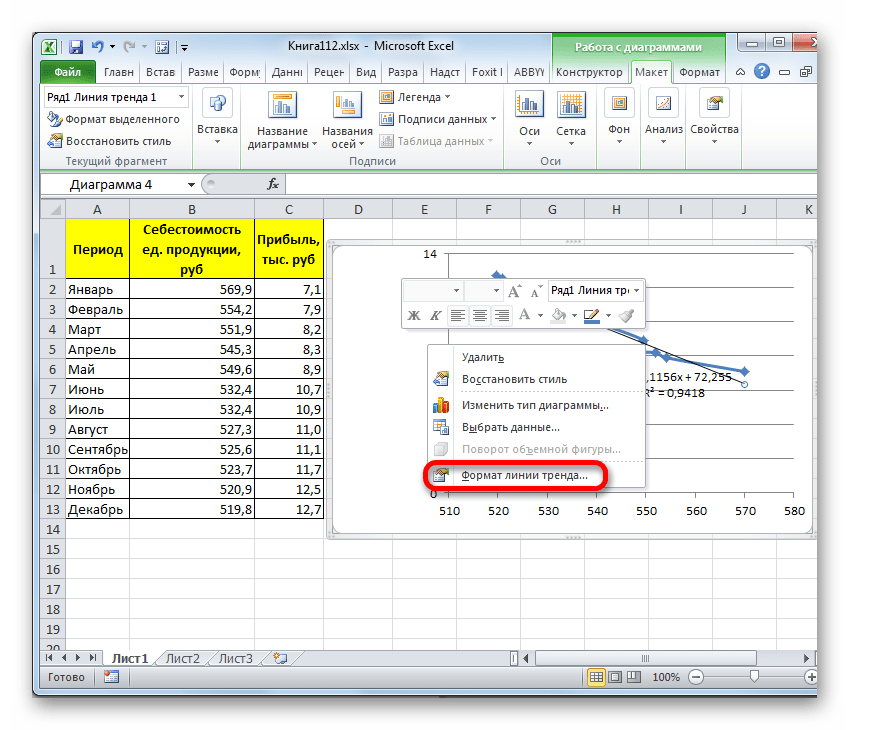
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
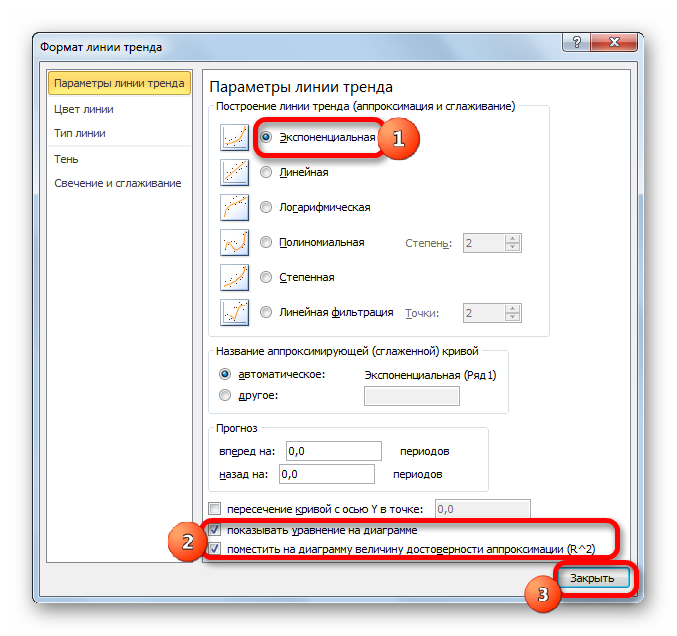
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
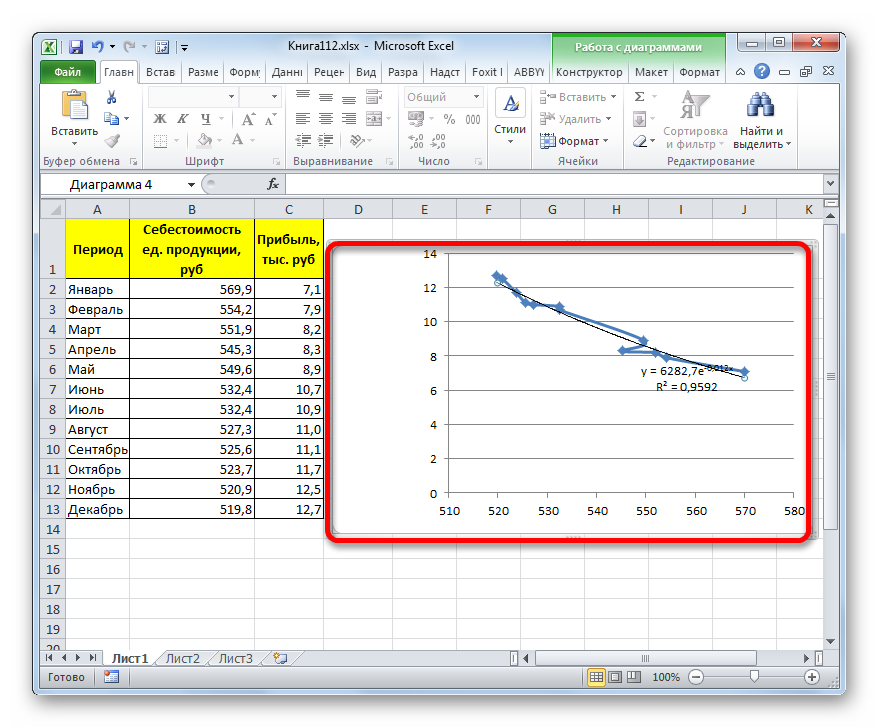
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
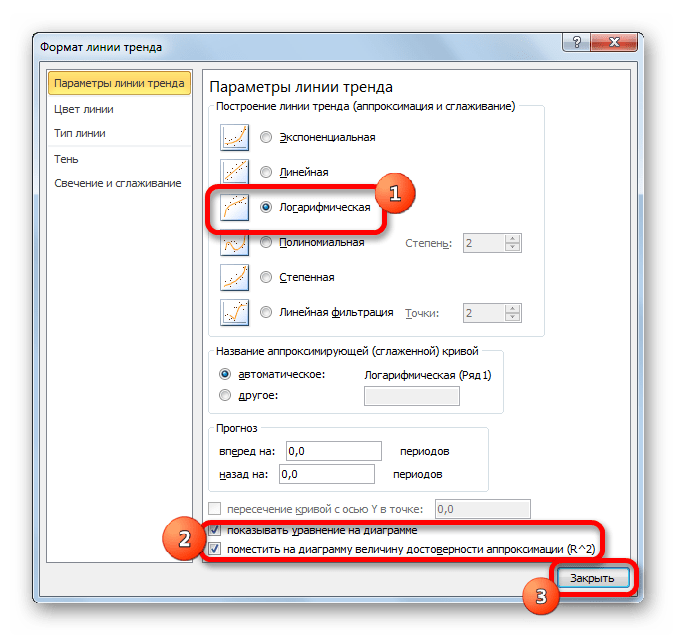
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
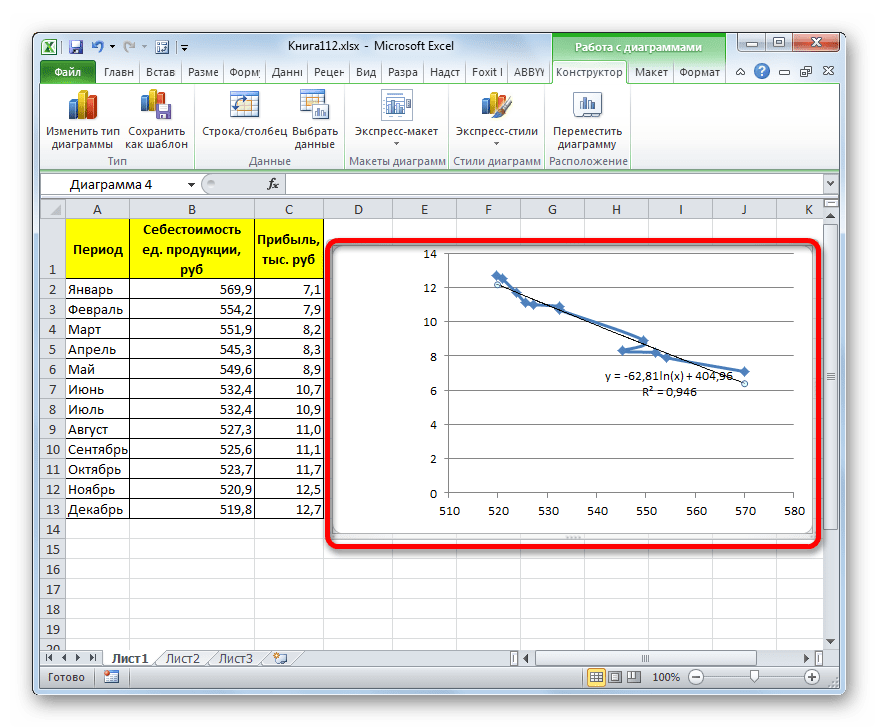
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
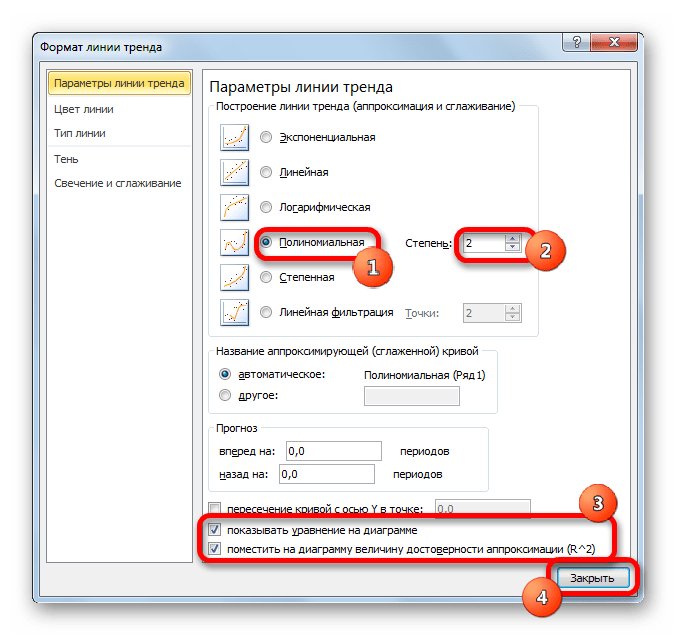
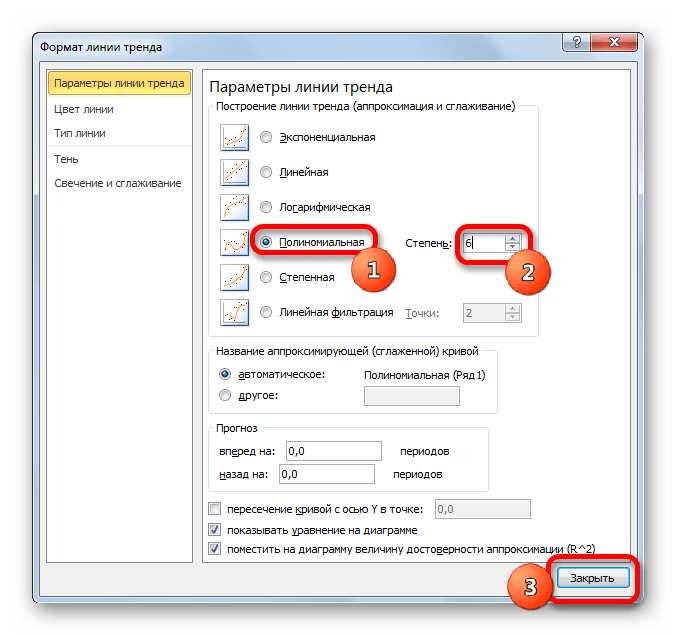
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
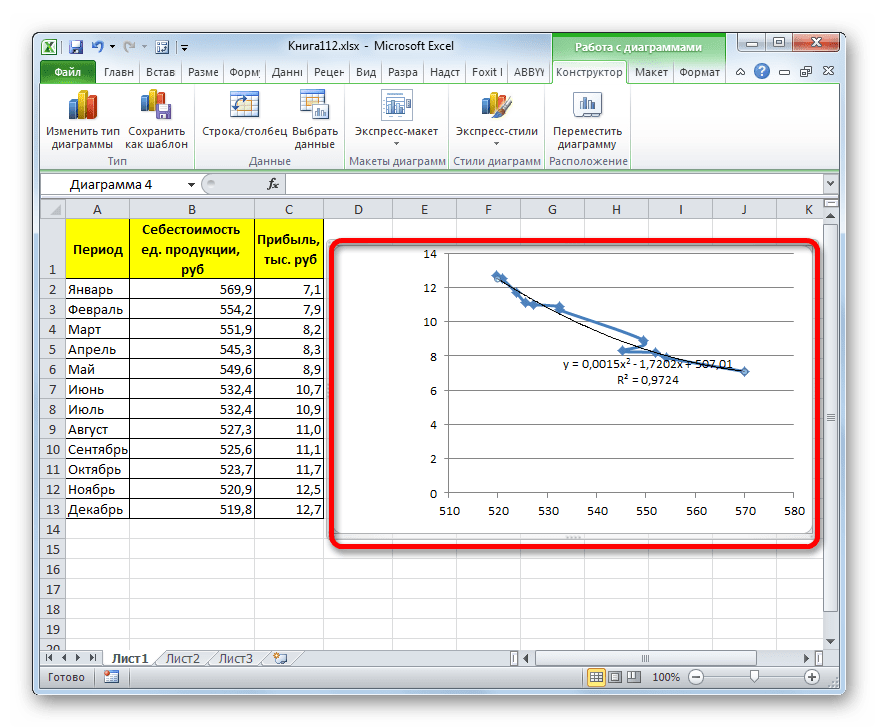
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
В нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
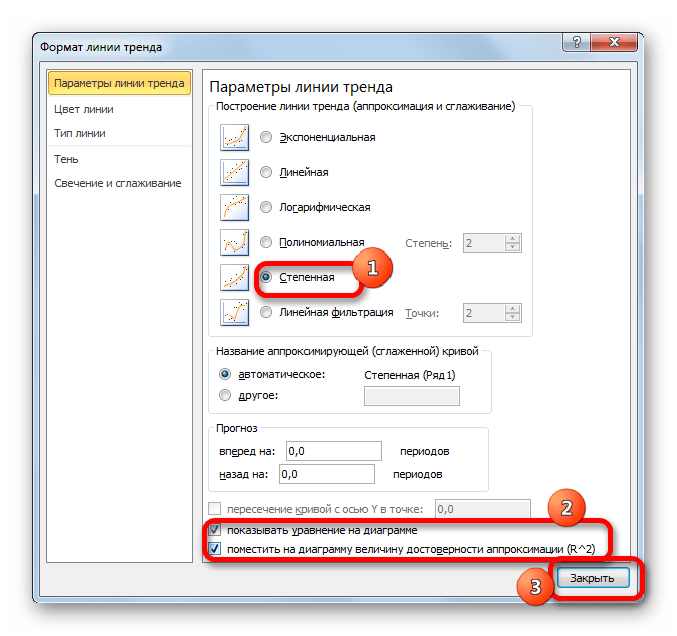
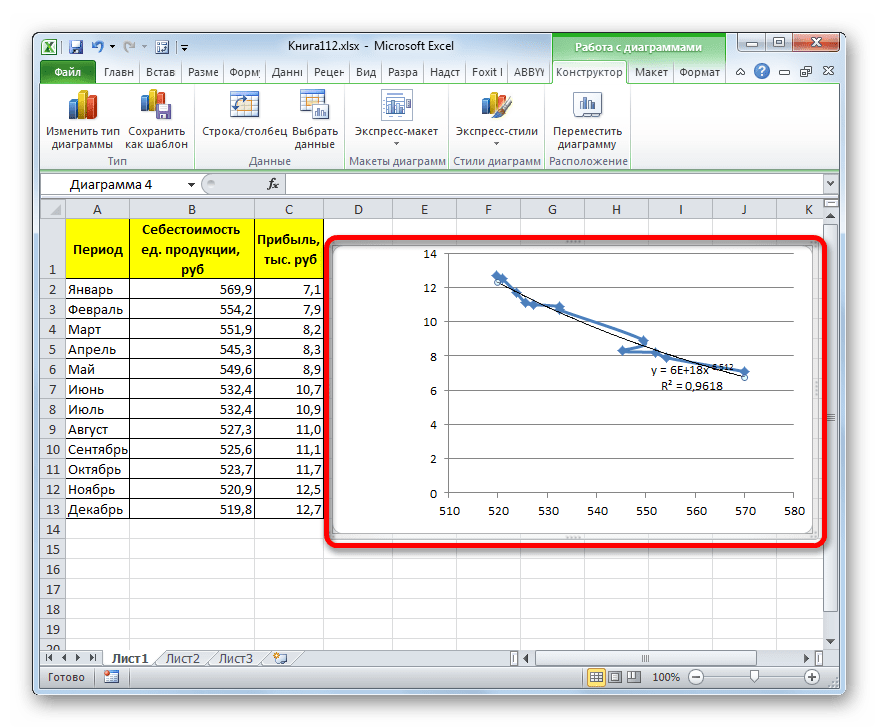
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Источник
17 авг. 2022 г.
читать 1 мин
Вы можете использовать функцию ЛИНЕЙН() в Excel, чтобы подобрать полиномиальную кривую с определенной степенью.
Например, вы можете использовать следующий базовый синтаксис, чтобы подогнать полиномиальную кривую со степенью 3:
=LINEST( known_ys , known_xs ^{1, 2, 3})
Функция возвращает массив коэффициентов, описывающих полиномиальную подгонку.
В следующем пошаговом примере показано, как использовать эту функцию для подбора полиномиальной кривой в Excel.
Шаг 1: Создайте данные
Во-первых, давайте создадим некоторые данные для работы:
Шаг 2: Подберите полиномиальную кривую
Далее воспользуемся функцией ЛИНЕЙН() , чтобы подобрать полиномиальную кривую степени 3 к набору данных:
Шаг 3: Интерпретация полиномиальной кривой
Как только мы нажмем ENTER , появится массив коэффициентов:
Используя эти коэффициенты, мы можем построить следующее уравнение, описывающее взаимосвязь между x и y:
у = 0,0218x 3 – 0,2239x 2 – 0,6084x + 30,0915
Мы также можем использовать это уравнение для вычисления ожидаемого значения y на основе значения x.
Например, предположим, что x = 4. Ожидаемое значение y будет следующим:
у = 0,0218(4) 3 – 0,2239(4) 2 – 0,6084(4) + 30,0915 = 25,47
Дополнительные ресурсы
Как выполнить полиномиальную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как добавить квадратную линию тренда в Excel
В рамках подготовки курса для бакалавров МФТИ я понял, что в моем блоге не так много заметок по использованию Excel в математике и физике. Каково же было мое удивление, когда я обнаружил, что книг по этой теме на русском языке буквально единицы. Ранее я опубликовал Вильям Дж. Орвис. Excel для ученых, инженеров и студентов. В заметке представлены три варианта нахождения интерполяционного полинома Лагранжа: таблица на листе Excel, функция VBA, функция листа Excel на основе REDUCE и LAMBDA. В заметке использованы материалы книги Алексея Васильева Числовые расчеты в Excel. Бумажная и электронная версии книги доступны на сайте издательства.
Рис. 1. Вычисление интерполяционного полинома по методу Лагранжа; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Скачать заметку в формате Word или pdf, примеры в архиве (внутри файл Excel с поддержкой макросов)
Алгоритм
Задача интерполирования обычно решается для того, чтобы «восстановить» по набору дискретных данных аналитическую функциональную зависимость. Нередко в качестве функции, на основе которой строится интерполяционная зависимость, выбирают полиномиальные выражения. Предположим, имеется набор узловых точек х1, х2, …, хn и набор значений y1, y2, …, yn неизвестной функции в этих точках. Задача – построить зависимость f(x) такую, чтобы соответствующая кривая проходила через все точки (xk, yk) (k = 1, 2, …, n), т.е. необходимо, чтобы для всех k выполнялись соотношения f(xk) = yk.
Для однозначного определения коэффициентов интерполяционного полинома его степень должна быть на единицу меньше, чем количество точек, по которым выполняется интерполирование. Технически коэффициенты полинома можно вычислить несколькими методами. Наиболее популярны полином Лагранжа и полином Ньютона.
Схема Лагранжа предполагает, что соответствующее полиномиальное выражение, построенное по точкам (х0, y0), (х1, y1), …, (хn, yn), ищется в виде
Полином имеет степень n, поскольку строится по n + 1 точке: индексация точек (хm, уm) начинается с нуля, а последний индекс равен n. Функции ϕm(х) являются полиномами степени n, причем такими, что в узловых точках xk имеют место соотношения: ϕm(хk) = 0, если k ≠ m, и ϕm(хk) = 1, если k = m. Эти полиномы вычисляются в виде произведений
для всех m = 0, 1, 2, …, n.
Метод Лагранжа в таблице на листе Excel
Реализуем метод Лагранжа в Excel для табулированной по 11 равноудаленным узловым точкам (на интервале значений аргумента от -2π до 2 π) функции
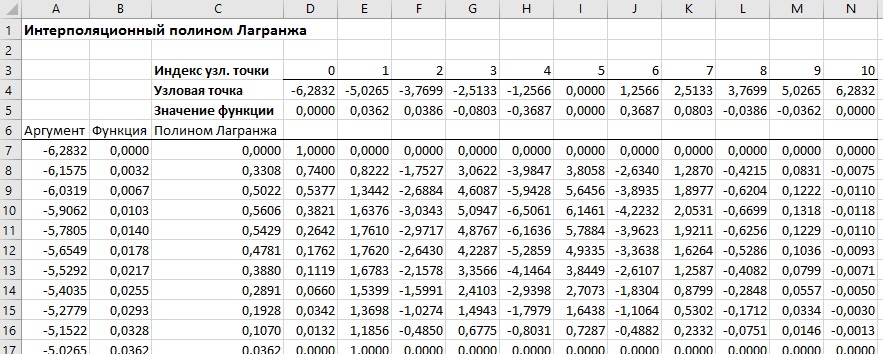
См. рис. 1. В столбце А – аргумент, В – значение функции, С – значения интерполяционного полинома построенного по методу Лагранжа. Количество точек в столбце А зависит от целей интерполяции. Поскольку мы далее хотим построить график, точек выбрано много и они расположены равномерно на интервале интерполяции. Частота этих точек значительно выше, чем частота узловых точек, на основе которых создается полином.
Ячейки D4:N4 содержат значения узловых точек, на основе которых мы создаем интерполяционный полином. Значения полинома в узловых точках отображаются в ячейках D5:N5. В ячейках D3:N3 указаны индексы узловых точек.
Основные вычисления выполняются в ячейках D7:N107 и, как результат, в ячейках С7:С107 вычисляются значения интерполяционного полинома в точках, которые указаны в ячейках А7:А107. В ячейках D7:N107 содержатся значения функций ϕm(х) для разных аргументов интерполяционного полинома х и разных индексов узловых точек m. В каждой строке диапазона D7:N107 находятся значения функций ϕm(х) для одного и того же аргумента х, но разных индексов m. В столбцах диапазона D7:N107 содержатся значения для разных аргументов х, и одного и того же индекса m. В диапазоне D7:N107 три типа формул: для левого D7: D107 и правого N7:N107 краев и остальных столбцов Е7:М107. С формулами можно ознакомиться в приложенном Excel-файле.
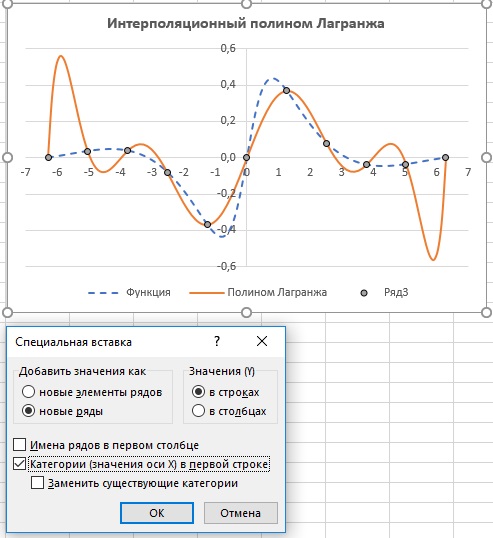
Выделите диапазон А7:С107 и постройте график. Чтобы добавить узловые точки, скопируйте диапазон D4:N5 в буфер обмена, выделите диаграмму, пройдите Главная –> Вставить –> Специальная вставка. Настройте параметры в окне Специальная вставка. Нажмите Ok. Отформатируйте вставленный ряд: отмените линию и добавьте встроенный маркер.
Рис. 2. График функции f(x) = sin(x)/(1 + x2), интерполяционный полином Лагранжа и узловые точки
Видно, что вычисленные нами значения интерполяционного полинома в узловых точках совпадают со значениями функции. В других точках совпадение не столь хорошее. К сожалению, значительные осцилляции на границах интервала интерполирования являются типичными для этого метода.
Функция VBA
Можно упростить вычисления и отказаться от громоздкой промежуточной таблицы с вычислениями, если воспользоваться кодом VBA.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
Function ЛАГРАНЖ(Px As Range, Py As Range, z As Variant) As Double ‘ Переменная для запоминания аргумента полинома Dim x As Double ‘ Значение аргумента полинома x = z ‘ Переменная для запоминания количества узловых точек Dim n As Integer ‘ Вычисляем количество узловых точек n = Px.Count ‘ Целочисленные переменные для операторов цикла Dim i As Integer, j As Integer ‘ Переменная для вычисления значения полинома Dim L As Double ‘ Начальное значение для полиномиальной суммы L = 0 ‘ Переменная для вычисления произведения Dim phi As Double ‘ Внешний цикл For i = 1 To n ‘ Начальное значение для произведения phi = 1 ‘ Первый внутренний цикл For j = 1 To i — 1 ‘ Умножаем на разность аргумента и узловой точки phi = phi * (x — Px.Cells(j).Value) ‘ Делим на разность узловых точек phi = phi / (Px.Cells(i).Value — Px.Cells(j).Value) Next j ‘ Второй внутренний цикл For j = i + 1 To n ‘ Умножаем на разность аргумента и узловой точки phi = phi * (x — Px.Cells(j).Value) ‘ Делим на разность узловых точек phi = phi / (Px.Cells(i).Value — Px.Cells(j).Value) Next j ‘ К полиномиальной сумме добавляем очередное слагаемое L = L + phi * Py.Cells(i).Value Next i ‘ Результат вычислений ЛАГРАНЖ = L End Function |
Пояснение кода
Функция ЛАГРАНЖ() имеет три аргумента: диапазон ячеек со значениями узловых точек (Рх), диапазон ячеек со значениями интерполируемой функции в узловых точках (Ру), а также аргумент, для которого вычисляется значение интерполяционного полинома Лагранжа (z). Функция возвращает числовой результат типа Double.
Поскольку третий аргумент функции может быть как числовым значением, так и ссылкой на ячейку, в теле функции значение этого аргумента записываем в переменную х. Если третий аргумент – число, то процесс «переписывания» ничего не добавляет. Если же третий аргумент – ссылка на ячейку, то присваивание значения ячейки локальной числовой переменной позволяет снять неоднозначность в определении типа третьего аргумента.
Алгоритм использует количество узловых точек. Явно этот параметр в аргументе функции ЛАГРАНЖ() отсутствует. Но он вычисляется, как количество ячеек в диапазоне, переданном первым аргументом функции ЛАГРАНЖ(). Поэтому мы объявляем переменную n = Рх.Count. Свойство Count для диапазона возвращает количество ячеек.
Основные вычисления производятся в блоке из вложенных условных операторов. Для использования в этих операторах объявляются две целочисленные переменные i и j. В переменной L накапливается полиномиальная сумма, а в переменной phi произведение в соответствии с формулой (2).
Перед началом выполнения вложенных операторов цикла переменной L присваивается значение 0. Индексная переменная i во внешнем цикле пробегает значения от 1 до n. В начале каждой итерации переменной phi присваивается значение 1. После этого последовательно запускаются два идентичных цикла. Основное различие между ними – диапазон изменения индексной переменной j. Для первого цикла она изменяется от 1 до i-1, а для второго цикла — от i+1 до n. Таким образом, при фиксированном значении i переменная j пробегает все значения от 1 до n, за исключением значения i. За каждую такую итерацию переменная phi сначала умножается на величину (x-Px.Cells(j).Value), а затем делится на величину (Px.Cells(i).Value-Px.Cells(j).Value). Здесь следует учесть, что Рх.Сеlls(индекс).Value – это значение ячейки с указанным индексом в диапазоне Рх (т.е. это значение узловой точки).
После того как значение переменной phi (для данного значения i) вычислено, командой L = L+phi * Ру.Cells(i).Value к полиномиальной сумме добавляем очередное слагаемое. Здесь Py.Cells(i).Value – ссылка на значение ячейки в диапазоне Ру со значениями табулированной функции. В итоге значение переменной L возвращается как результат функции (команда ЛАГРАНЖ = L).
Работа функции ЛАГРАНЖ()
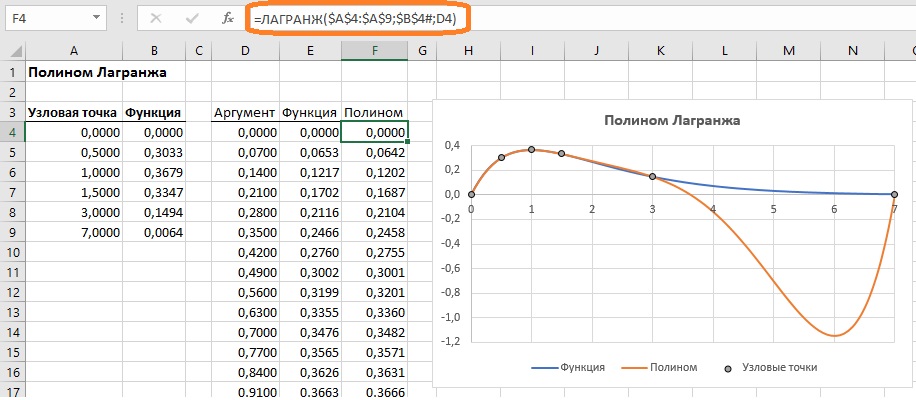
Функцию ЛАГРАНЖ() можно использовать на рабочем листе. Рассмотрим новый пример. Ячейки А4:В9 содержат данные об узловых точках и значениях функции f(x) = x*exp(-x). При этом в ячейках А4:А9 указаны несколько неравномерно распределенных на интервале от 0 до 7 точек.
Рис. 3. Пользовательская функции для вычисления интерполяционного полинома Лагранжа
Как мы отмечали ранее, интерполяционный полином не везде дает хорошее приближение для табулированной функции, даже с учетом того, что последняя достаточно плавная.
Вычисление полинома Лагранжа на основе функций REDUCE и LAMBDA
В декабре 2020 года Microsoft анонсировал функцию LAMBDA, которая позволяет определять пользовательские функции, написанные на языке формул Excel. А в июле 2021 г. объявил о создании новых функций, основанных на LAMBDA. Я недавно описал работу с LAMBDA и новыми функциями Excel. Не могу сказать, что написание сложных конструкций на основе этих функций проще, чем кода VBA, но как учебный пример, это весьма интересно.[1]
Код функции REDUCE
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
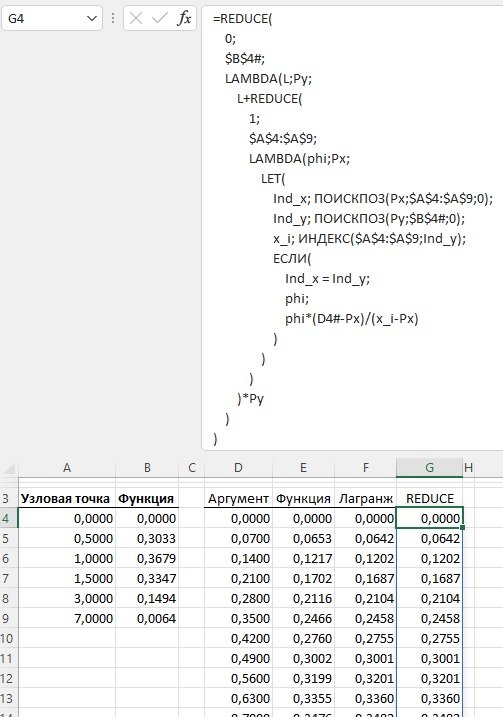
=REDUCE( 0; $B$4#; LAMBDA(L;Py; L+REDUCE( 1; $A$4:$A$9; LAMBDA(phi;Px; LET( Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0); Ind_y; ПОИСКПОЗ(Py;$B$4#;0); x_i; ИНДЕКС($A$4:$A$9;Ind_y); ЕСЛИ( Ind_x = Ind_y; phi; phi*(D4#-Px)/(x_i-Px) ) ) ) )*Py ) ) |
Описание работы функции REDUCE
Функция REDUCE работает, как обычная функция листа. Внутри ее могут располагаться ссылки на ячейки и динамические массивы. В отличие от функции LAMBDA, функция REDUCE не требует предварительного именования. Алгоритм работы функции REDUCE похож на алгоритм кода VBA в функции ЛАГРАНЖ(): один внешний цикл и один внутренний (в коде VBA два внутренних цикла). Внешний цикл перебирает все i значений диапазона В4:В9 (см. рис. 4), умножая на значения phi, определяемые для каждого i во внутреннем цикле. Во внутреннем цикле задается стартовое значение phi = 1. Далее для фиксированного i перебираются все j значений диапазона А4:А9, и для всех i ≠ j значение phi, полученное на предыдущем шаге, умножается на некое значение, а для i = j значение phi не изменяется. (Благодаря такой проверке, вместо двух внутренних циклов в коде VBA, здесь используется один.)
Посмотрим, как этот алгоритм реализован в коде функции REDUCE. Цель функции REDUCE – обработать массив, и вернуть одно число. Функции REDUCE имеет три аргумента. Первые два – начальное значение (0) и обрабатываемый массив ($B$4#).
Третий аргумент – функция обработки элементов массива
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
LAMBDA(L;Py; L+REDUCE( 1; $A$4:$A$9; LAMBDA(phi;Px; LET( Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0); Ind_y; ПОИСКПОЗ(Py;$B$4#;0); x_i; ИНДЕКС($A$4:$A$9;Ind_y); ЕСЛИ( Ind_x = Ind_y; phi; phi*(D4#-Px)/(x_i-Px) ) ) ) )*Py ) |
Рис. 4. Работа функции REDUCE
Функция LAMBDA принимает столько же параметров, сколько передает функция REDUCE:
L – накопитель; Py – массив. L – это то значение, которое вернется функцией после обработки всех элементов массива. Начальное значение L = 0. Это значение определено первым аргументом функции REDUCE. Ру – массив $B$4#. Функция LAMBDA накапливает значения L в элементе формулы L + REDUCE(… Эта запись аналогична более привычной для программистов L = L + REDUCE(…
Функция LAMBDA реализует внешний цикл. Она стартует со значения L = 0 и для всех элементов массива Ру (он же $B$4#) выполняет действие
Здесь реализована сумма произведений элементов Ру и рассчитанных коэффициентов, которые возвращаются внутренним циклом на основе REDUCE(…
Внутренний цикл также основан на REDUCE
|
REDUCE( 1; $A$4:$A$9; LAMBDA(phi;Px; LET( Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0); Ind_y; ПОИСКПОЗ(Py;$B$4#;0); x_i; ИНДЕКС($A$4:$A$9;Ind_y); ЕСЛИ( Ind_x = Ind_y; phi; phi*(D4#-Px)/(x_i-Px) ) ) ) ) |
Результат REDUCE – коэффициент для умножения на элемент массива Ру. Функция REDUCE принимает два аргумента
Начальное значение 1 и массив $A$4:$A$9. Внутри функции массив $A$4:$A$9 понижается до одного значения, путем последовательной обработки всех элементов массива $A$4:$A$9. Обработка выполняется по правилам, описанным внутри LAMBDA:
|
LAMBDA(phi;Px; LET( Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0); Ind_y; ПОИСКПОЗ(Py;$B$4#;0); x_i; ИНДЕКС($A$4:$A$9;Ind_y); ЕСЛИ( Ind_x = Ind_y; phi; phi*(D4#-Px)/(x_i-Px) ) ) ) |
LAMBDA принимает два параметра от REDUCE: начальное значение phi = 1 и массив Рх = $A$4:$A$9. Функция LET не выполняет расчеты, а позволяет упростить восприятие этого фрагмента формулы (подробнее см. здесь). LET определяет три переменные – индекс элемента массива $A$4:$A$9, обрабатываемого на текущем шаге:
|
Ind_x; ПОИСКПОЗ(Px;$A$4:$A$9;0); |
… индекс элемента массива $B$4#, переданного из внешнего цикла:
|
Ind_y; ПОИСКПОЗ(Py;$B$4#;0); |
… и значение элемента массива $A$4:$A$9, соответствующего индексу Ind_y из внешнего цикла:
|
x_i; ИНДЕКС($A$4:$A$9;Ind_y); |
Расчет функции LET происходит внутри оператора ЕСЛИ:
|
ЕСЛИ( Ind_x = Ind_y; phi; phi*(D4#-Px)/(x_i-Px) ) |
Для всех элементов массива, где Ind_x ≠ Ind_y накапливается новое значение phi:
Как обычно, эта запись эквивалента phi = phi*(…)
Если же индексы равны Ind_x = Ind_y, оставляем значение phi без изменения.
Ссылка на ячейку листа (D4#) – это ссылка на динамический массив аргументов, для которых вычисляется полином Лагранжа. На рис. 4 аргументы размещены в столбце D.
Поскольку использование REDUCE и LAMBDA – это всё же не классический цикл, мне не удалось найти вариант, как обращаться к элементу массива по его индексу. Поэтому в переменных Ind_x и Ind_y реализовано обращение по значению элемента: ПОИСКПОЗ(Px;$A$4:$A$9;0). Такой подход накладывает ограничения на аргументы и значения функции в узловых точках: не должно быть повторений. Если хотя бы в двух узловых точках значения функций совпадают, функция ПОИСКПОЗ() отработает не корректно.
[1] Это оригинальный метод. Он не описан в книге Алексея Васильева «Числовые расчеты в Excel».
|
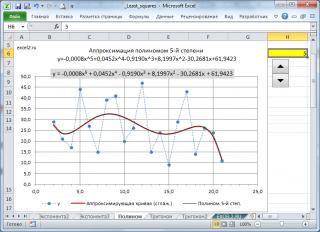
Уважаемые сопланетники! Столкнулся с проблемой, прошу помочь. Для аппроксимации передаточной характеристики измерительных приборов часто используют полином. С точки зрения электроники — это очень удобный способ, требующий от МК относительно мало ресурсов и предоставляющий очень хорошую точность. Для получения коэффициентов однофакторного полинома я традиционно использовал встроенную в Excel функцию ЛИНЕЙН. Однако в имеющейся в данный момент задаче выяснилось, что погрешность аппроксимации этим способом очень высока, — значительно выше, чем при использовании математических пакетов или линии тренда графика в Excel. Предположив, что проблема в некорректном использовании функции ЛИНЕЙН, перешерстил интернет, пробовал сторонние файлы. Оказалось, проблема известная, и связана она с алгоритмом работы этой функции (подробности я не понял, в математике не очень). Я взял одну и ту же выборку и сравнил четыре способа получения коэффициентов:
первый способ (ЛИНЕЙН) даёт примерно в 1,5…2 раза бОльшую погрешность, чем другие . и ЛИНЕЙН , и Agraph дают погрешность в 4 раза больше , чем два последних . Хотелось бы все действия максимально автоматизировать и привязать к Excel. Возможно, можно как-то исхитриться и заставить ЛИНЕЙН работать по другому? p.s. Движок запрещает грузить файлы свыше 100к, поэтому нарезал скринов. |
|
|
МатросНаЗебре Пользователь Сообщений: 5516 |
#2 03.12.2021 14:29:35 Коэффициенты можно найти формулами:
И через VBA.
Изменено: МатросНаЗебре — 03.12.2021 15:02:39 |
||||
|
tutochkin Пользователь Сообщений: 559 |
#3 03.12.2021 14:47:41
Да, есть. тут выкладывал решение
Однако обратите внимание, что далеко не всегда коэфф-ты вытаскиваются верно. Я в практике с таким не сталкивался, но такое имеет место быть Тут выкладывали проблему. Поэтому в своих расчётах применяю кусочную интерполяцию… Изменено: tutochkin — 03.12.2021 15:02:10 |
||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#4 07.12.2021 11:23:02 Благодарю за подсказки, пробую использовать. На VBA не писал очень давно, попал в ступор. Пытаюсь например, так, получаю ошибку:
Чувствую, не учёл какую-то мелочь, а сообразить не могу.. |
||
|
tutochkin Пользователь Сообщений: 559 |
#5 07.12.2021 13:06:23 Алексей Назаров,
Изменено: tutochkin — 07.12.2021 13:07:24 |
||
|
Цель — получить коэффициенты аппроксимирующего полинома 5-6 порядка по исходной выборке, находящейся в книге Excel. Почему именно Excel — в ней я собираю данные с измерительных приборов (с помощью VBA), управляю внешними устройствами (с помощью VBA же), обрабатываю полученные данные и т.п., и любой прыжок в сторону превращается в неудобный костыль… И при экспериментах часто вариантов данных очень много, каждый нужно обработать, проверить и т.п. Изменено: Алексей Назаров — 08.12.2021 10:17:38 |
|
|
tutochkin Пользователь Сообщений: 559 |
#7 07.12.2021 13:54:31 Алексей Назаров, ну вытащить коэфф-ты из того что я выше привёл совсем не сложно — они там уже есть (матрица с). Однако они не будет отличаться от =ИНДЕКС(ЛИНЕЙН(F4:F13;E4:E13^{1;2;3;4;5;6});1;1) , проверено
Понятие точности относительно. Вот на рисунке несколько видов интерполяции через одни и те-же опорные точки…. А какая разница в промежутках
Изменено: tutochkin — 07.12.2021 14:16:00 |
||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#8 07.12.2021 13:58:25 Ага, уже что-то получается! На команду
Получаю результат: 4,7737E-38 * X ^ 6 -5,455E-30 * X ^ 5 + 2,1638E-22 * X ^ 4 -3,0827E-15 * X ^ 3 + 0 * X ^ 2 + 0 * X ^ 1 + 5512600 Осталось «раздербанить» строку на составляющие, но есть одно большое НО: в результате всего 5 значащих цифр….. Кроме того, значения коэффициентов отличаются… Теоретически, как здесь: |
||
|
tutochkin Пользователь Сообщений: 559 |
#9 07.12.2021 15:01:02
Так этот макрос и выводит полную формулу… Там же написано — «‘ Программа формирования текста уравнения по всем точкам»
Так это в макросе и прописано… Format(Application.Index(WorksheetFunction.LinEst(yn, xn, True, True), 1, k), «0.####E+») увеличивайте, или вообще удалите.
=ИНДЕКС(Koef($D$5:$D$12;$E$5:$E$12;6);1;G5) — вывод элементов
Да, это известная проблема при больших Х. Изменено: tutochkin — 07.12.2021 15:17:32 |
||||||||||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#10 08.12.2021 09:48:48
Какой инженер читает инструкции? )))
Да, благодарю, разрядность получил.
Сейчас попробую
К сожалению…. В самом первом сообщении в этой ветке я постарался подробно расписать, почему именно меня не удовлетворяют коэффициенты, полученные функцией ЛИНЕЙН. И цель этой ветки была следующей: Спасибо за помощь, буду пробовать дальше. tutochkin , два последних фрагмента кода — это что? Дают ли они коэффициенты, отличные от ЛИНЕЙН, или то же самое? |
||||||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#11 08.12.2021 09:52:34
Боюсь, большие Х здесь не главная причина.
Вы привели пример интерполяции, у меня — аппроксимация, причём количество точек не просто превышает порядок полинома, оно составляет от нескольких десятков до нескольких тысяч. В измерительных устройствах является стандартом де-факто использование именно полиномиальной аппроксимации. Фактически, этот способ полностью и меня удовлетворяет, остался один нюанс — нужно выработать инструмент для удобного расчёта адекватных коэффициентов. )) P.S. Сейчас попробую разобраться в примерах МатросНаЗебре , может, здесь что получится. |
||||
|
tutochkin Пользователь Сообщений: 559 |
#12 08.12.2021 11:09:11
так я про это и писал:
а куда 4…20мА дели ?
Вот это зря. |
||||||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#13 08.12.2021 12:06:10
4..20 кануло в лету.
Виноват, исправлюсь! ))) Сейчас разбираюсь со свойством .DataLabel.Text, пытаюсь корректно выдернуть из него данные. |
||||
|
tutochkin Пользователь Сообщений: 559 |
#14 08.12.2021 13:03:54
Да вот не правда. 99% КИПиА на новых станциях на нём. Все метраны ДД ДИ (да и Метран-280, Метран-2700) на 4-20 с харт протоколом. Сименс аналогично. А вот потом уже идёт преобразование хоть по среднемедианному хоть по среднеарефметическому. Но это не суть. Для моих работ выковыривание из лэйблов никуда не годится, посему не рассматривалось. |
||
|
Алексей Назаров Пользователь Сообщений: 24 |
#15 08.12.2021 13:20:40
Вот именно, что с HART протоколом, т.е. от 4-20 осталось, фактически, только питание и характеристики физического уровня передачи данных.
Это не преобразование, это усреднение/фильтрация, её делают, в зависимости от конкретного применения.
Для моих годится всё, что НОРМАЛЬНО РАБОТАЕТ. Сейчас разбираюсь с .DataLabel.Text, данные получить удаётся, но либо при пошаговом выполнении кода, либо, если в тексте есть ошибка, вызывающая остановку компилятора. После пропуска ошибки данные и появляются. (((
|
||||||||
|
tutochkin Пользователь Сообщений: 559 |
#16 08.12.2021 13:26:21
Ну во первых вы так и не показали как считаете погрешность. Во вторых — интерполируйте кусочным способом и получите в узлах 0-ю погрешность. |
||
|
Алексей Назаров Пользователь Сообщений: 24 |
#17 08.12.2021 14:29:14
Под погрешностью аппроксимации я имею в виду максимальную разницу между любой точкой экспериментальных данных и соответствующей точкой, вычисленной по полиному, построенному по этим данным. В том числе и между узлами. Например, для проверки качества полинома можем сделать 1000 измерений, по 100 точкам (каждой 10-й) построить полином, а погрешность проверить по всем 1000 точкам. И между узлами погрешность не менее важна, чем в узлах! Кусочно-линейную пробовали, но при разумном количестве точек (не более нескольких десятков) погрешность аппроксимации наших данных превышает 0,03%, а нужно не более 0,01%. |
||
|
tutochkin Пользователь Сообщений: 559 |
#18 08.12.2021 14:45:35
При кусочной интерполяции в узловых точках погрешность нулевая. Точно так же как и при интерполяцией сплайном. Между узлов зависит от типа функции интерполяции и граничных условий. Рисунки приводил выше.
Т.е. вы с помощью аппроксимации фильтруете точки и говорите о погрешности аппроксимации? Серьёзно? Не пробовали в начале хотя бы по медианному фильтру откинуть шумы? |
||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#19 08.12.2021 15:46:31
Мне не важна погрешность в узловых точках, важна В ЛЮБОЙ точке в заданном интервале. И этого КЛ не обеспечивает.
Не фильтрую, Вы не так поняли (или я неясно объяснил), но при исследовании иногда это использую.
Тут согласен, полноценные (даже сильно урезанные) файлы в лимит не влазят, а кидать на файлообменники не с руки было. |
||||||
|
tutochkin Пользователь Сообщений: 559 |
#20 08.12.2021 17:09:14
А Вы?
Чушь. Говорю как человек почти 20 лет занимающийся экспериментами на энергетическом оборудовании. Включая проведение гарантийных испытаний турбин Siemens и GE. Хорошим является только верный метод. А остальное называется подгон под условия. |
||||
|
Алексей Назаров Пользователь Сообщений: 24 |
#21 09.12.2021 08:48:06
Вы читаете через строчку. аппроксимации (а не о полной погрешности измерений), и везде старался это подчёркивать. Во-вторых, даже если говорить о полной погрешности, то параметры определяются на готовом изделии по эталонному прибору. На любой промежуточной точке , включая рекомендованные ГОСТами для данных СИ.
На первом графике числа по оси Y обрезаны, извините, недоглядел. Шум +-2…3 емзр от полного значения 30000…150000 это примерно 0,01…0,0015% от измеренного значения. т.е. не более 0,002%FS, это немного ниже, чем 50%? Кстати, и ошибка аппроксимации (по коэффициентам Октавы и линии тренда) в данном случае максимальная около 1,9ЕМЗР, т.е. находится на уровне шумов эталонного прибора. Думаю, при использовании более высокоточного СИ и погрешность аппроксимации будет ниже.
Вот именно, Вы занимаетесь метрологией, а я нормативными актами и МИ не особо ограничен, я больше исследователь-разработчик. В любом случае спасибо Вам за помощь, что помогли разобраться. Хоть этот метод нам и не подошёл, но отрицательный результат — тоже результат! P.S. Добавил файлы с выборками. Прикрепленные файлы
Изменено: Алексей Назаров — 09.12.2021 08:57:15 |
||||||
|
О, вроде получилось загрузить файл на 260 кБ, а ранее выше 100 не получалось. |
|
|
МатросНаЗебре Пользователь Сообщений: 5516 |
#23 09.12.2021 10:21:46 Вариант, возвращающий коэффициенты полинома.
|
||
|
tutochkin Пользователь Сообщений: 559 |
#24 09.12.2021 10:34:37
Я так и не увидел как Вы её считаете. Судя по приложенному файлу — контроль отклонений в заданных точках.
Это Вы про меня? Серьёзно?
Я не занимаюсь метрологией. Но моя работа требует знаний по средствам измерений, как раз из-за того что некоторые делают на глаз, а потом баланс расходов не сходится. |
||||||
|
alenco Пользователь Сообщений: 24 |
#25 09.12.2021 10:57:53 МатросНаЗебре, большое спасибо за (почти) правильно работающий код! У меня вылезает ошибка 9 (Subscript out of range) на строке
После замены формата числа на экспоненциальный
ошибка пропала, но и признаки работы ограничились перерисовкой экрана… Попробовал тормознуть код перед
И… вуаля! Осталась мелочь — обойтись без остановки кода. Такая проблема обсуждалась, например, здесь , здесь , попадалось и на других форумах, но панацеи никто не знает. Изменено: alenco — 09.12.2021 11:00:48 |
||||||
|
tutochkin Пользователь Сообщений: 559 |
#26 09.12.2021 11:13:56
И Вас ничего не смущает? |
||
|
alenco Пользователь Сообщений: 24 |
#27 09.12.2021 11:23:50
Судя по скрину, всё увидели и даже для своего варианта посчитали?
Не знаю, с функцией kus_interp я не знаком. Я когда-то пробовал КЛ на своих выборках, при небольшом количестве опорных точек (по моему, 10 или 20, уже не помню) она дала приличную погрешность. Дальше не заморачивался, остановился полностью на полиномах, по образцу предприятий, с кем мы работаем. Изменено: alenco — 09.12.2021 11:24:26 |
||||
|
alenco Пользователь Сообщений: 24 |
#28 09.12.2021 11:27:14
Кроме малого количества значащих цифр на вашем скрине — ничего. Если Вы про необходимость остановки кода — я верю, что эта проблема будет решена. Изменено: alenco — 09.12.2021 11:31:18 |
||
|
tutochkin Пользователь Сообщений: 559 |
#29 09.12.2021 12:01:05
Читайте не через строчку — давал вариант. Урезанный правда, только с линейным вариантом, но давал.
У как всё запущено… А ещё на глаз погрешности определяете. А зачем сменили Имя-фамилию на ник? |
||||
|
МатросНаЗебре Пользователь Сообщений: 5516 |
#30 09.12.2021 13:20:31 Вариант, вычисляющий коэффициенты через решение системы линейных уравнений. Точность хуже, чем у метода, через уравнение из линии тренда. Вероятно, точность теряется при работе с длинными числами.
Изменено: МатросНаЗебре — 09.12.2021 14:35:22 |
||