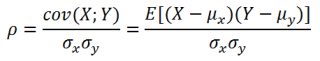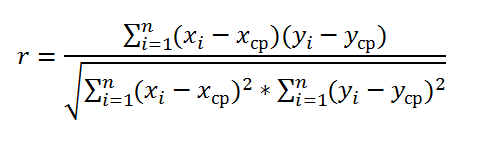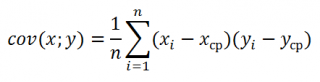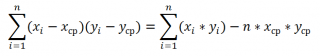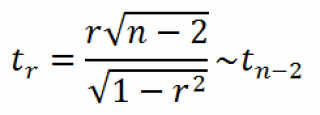Глава 4. Корреляция и регрессия
Большинство
изучаемых величин и характеристик как
в естествознании, так и социальных
науках, являются зависимыми. Совокупность
изучаемых величин подвержена, как
правило, воздействию случайных факторов.
В связи с этим возникают, помимо привычной
строгой функциональной зависимости
переменных величин, так называемая
статистическая зависимость и ее частный
случай – корреляционная. Изучение и
анализ корреляционных связей позволяют
сделать важные выводы, необходимые в
практических целях.
§4.1. Статистическая и корреляционная зависимости. Коэффициент корреляции. Корреляционный момент
Виды
зависимостей переменных величин.
Функциональной
называется зависимость между двумя
переменными величинами, при которой
значению одной переменной величины
соответствует одно определенное значение
другой.
Статистической
называется зависимость случайных
величин, при которой каждому значению
одной их них соответствует закон
распределения другой, то есть изменение
одной из величин влечет изменение
распределения другой.
Корреляционной
называется статистическая зависимость
случайных величин, при которой изменение
одной из величин влечет изменение
среднего значения другой.
Условные
средние. Линии регрессии.
Условным
средним
называется среднее арифметическое
наблюдаемых значений величины Y,
вычисленное при условии, что величина
Х
приняла конкретное фиксированное
значение х.
Условным
средним
называется среднее арифметическое
наблюдаемых значений величины
Х, вычисленное
при условии, что величина Y
приняла конкретное фиксированное
значение у.
Уравнение,
связывающее наблюдаемые значения
величины Х
и условную среднюю
величины Y,
называется уравнением
регрессии
Y
на Х:
.
Уравнение,
связывающее наблюдаемые значения
величины Y
и условную среднюю
величины Х,
называется уравнением
регрессии
Х на
Y:
.
Линии
на координатной плоскости, соответствующие
уравнениям регрессии называются линиями
регрессии.
Корреляционные
зависимости могут выражаться уравнениями
регрессии различных видов: линейной,
параболической, гиперболической,
показательной и т.д.
Корреляционный
момент и коэффициент корреляции.
Мерой
корреляционной зависимости двух
случайных величин Х
и Y
служит корреляционный
момент (или
ковариация),
который вычисляется по формуле:
, (4.1)
где
средние значения (здесь и в дальнейшем
предполагается, что каждая пара значений
(хi,yi)
наблюдалась по одному разу):
,
,
. (4.2)
Если
случайные величины Х
и Y
независимы, то для них mxy=0.
Из
определения корреляционного момента
следует, что его размерность равна
произведению размерностей изучаемых
величин, Это означает, что значение
корреляционного момента двух величин
зависит от выбора единиц измерения этих
величин. Поэтому для оценки связи величин
вводится другая величина, независящая
от размерности измеряемых величин и
называемая коэффициентом корреляции.
Коэффициентом
корреляции
двух измеряемых величин Х
и Y
называется величина:
, (4.3)
где
sх
и sу
– стандартные отклонения соответственно
величин Х
и Y.
Поскольку
размерность корреляционного момента
равна произведению размерностей величин
Х и Y,
а стандартные отклонения имеют размерности
этих величин, то коэффициент корреляции
является безразмерной величиной, и
поэтому он не зависит от выбора единиц
измерения изучаемых величин.
Свойства
коэффициента корреляции:
1)
Если две случайные величины Х
и Y
независимы, то их коэффициент корреляции
равен нулю, т.е. r=0.
2)
Модуль коэффициента корреляции не
превышает единицы, т.е. |r|£1,
что эквивалентно двойному неравенству:
-1£r£1.
Коэффициент
корреляции, вычисленный по данным
выборки, называется выборочным
и обозначается rв.
Вычисление
в Excel
корреляционных характеристик.
Ковариация
(корреляционный момент) (4.1) вычисляется
в Excel
с помощью стандартной статистической
функции КОВАР. Аргументом этой функции
являются диапазоны ячеек, содержащие
значения наблюдаемых величин
и
.
Например, если значения
содержатся в интервале А1:А10, а значения
содержатся в интервале В1:В10, то ковариация
этих величин вычисляется по формуле:
=КОВАР(А1:А10; В1:В10).
Коэффициент
корреляции (4.3) вычисляется в Excel
одной из двух функций: КОРРЕЛ или ПИРСОН.
Эти функции выдают одинаковый результат,
если значения наблюдаемых величин
записаны в виде чисел. Аргументы у этих
функций точно такие же, как и у функции
КОВАР, т.е. КОРРЕЛ(А1:А10;В1:В10) или
ПИРСОН(А1:А10;В1:В10).
Иногда
необходимо вычислять квадрат коэффициента
корреляции, для этого имеется функция
КВПИРСОН, выдающая значение r2.
Аргументы у этой функции такие же, как
и у трех предыдущих.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
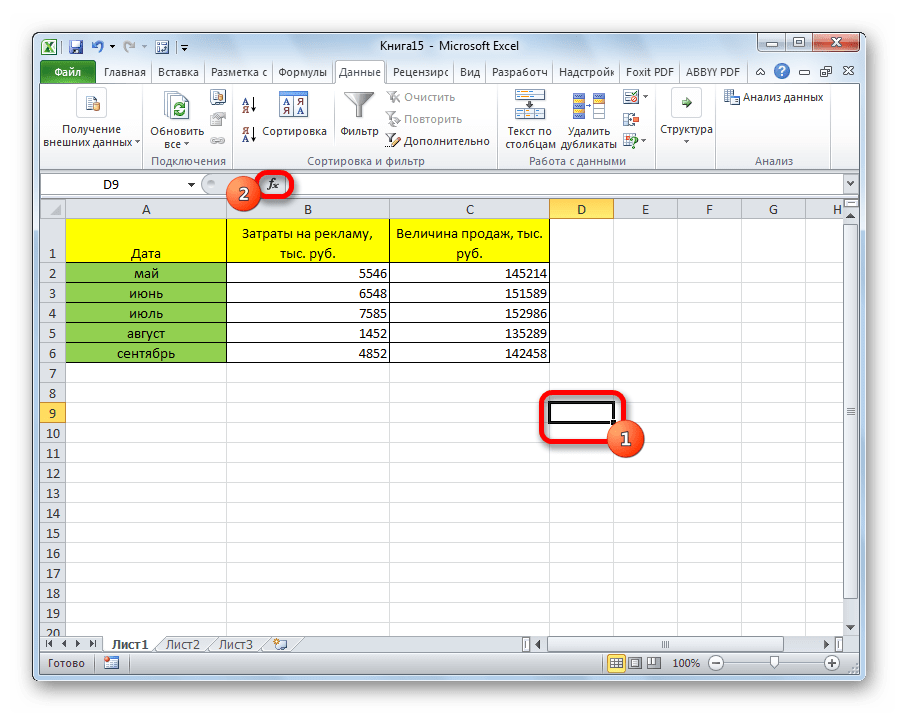
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
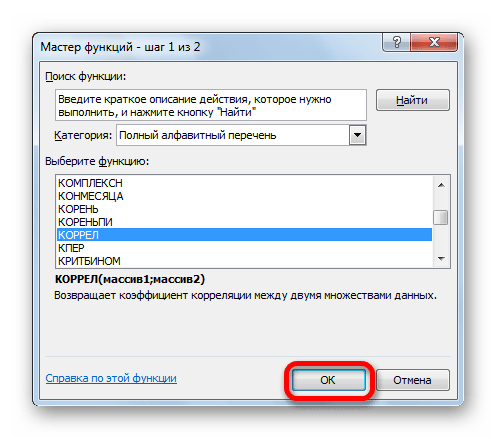
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
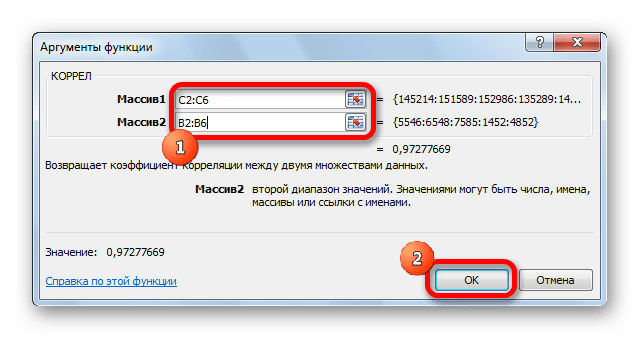
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
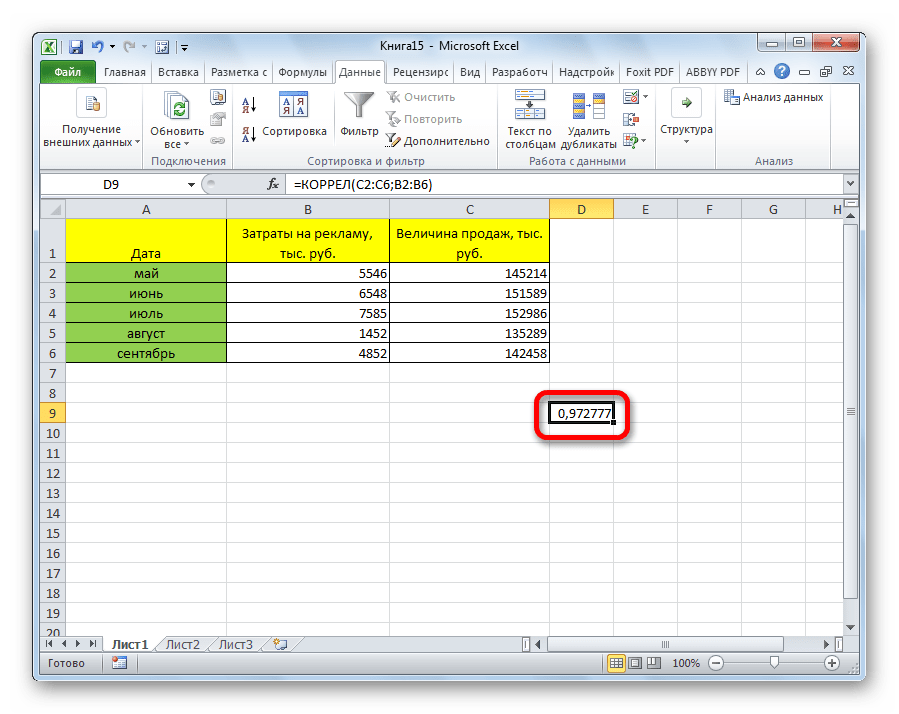
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
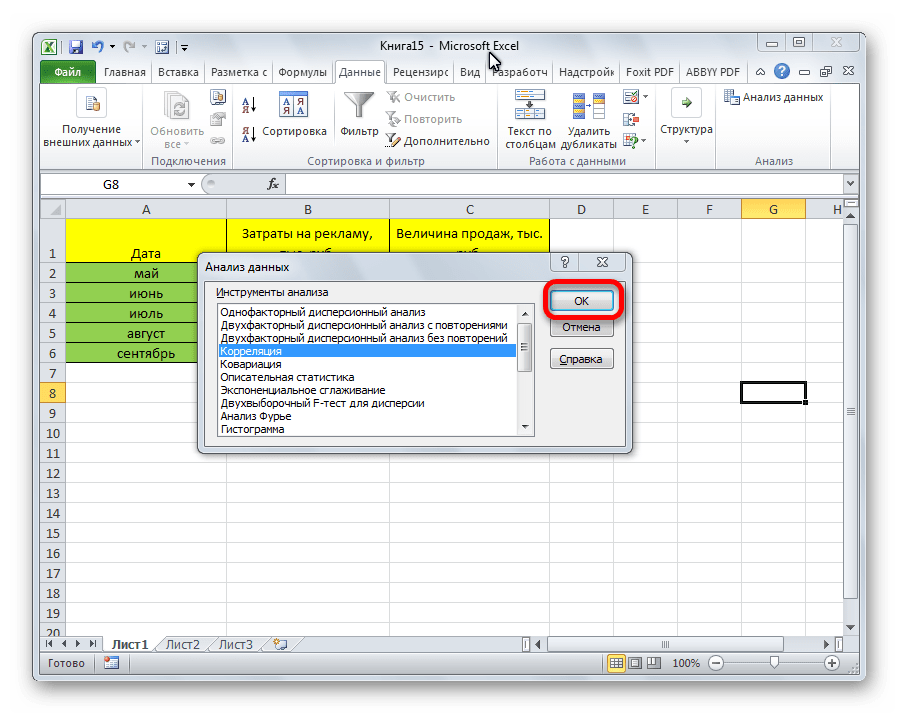
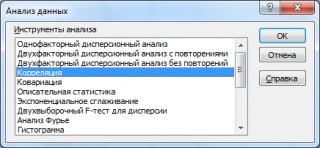
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
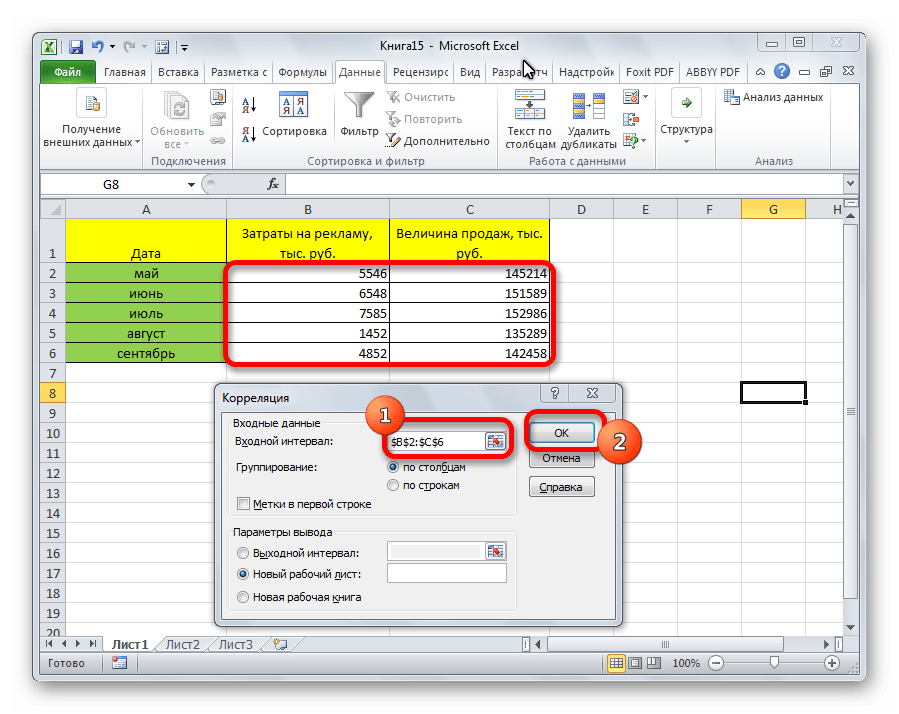
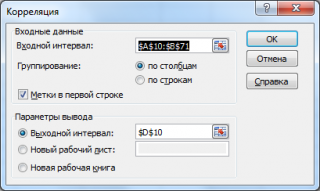
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
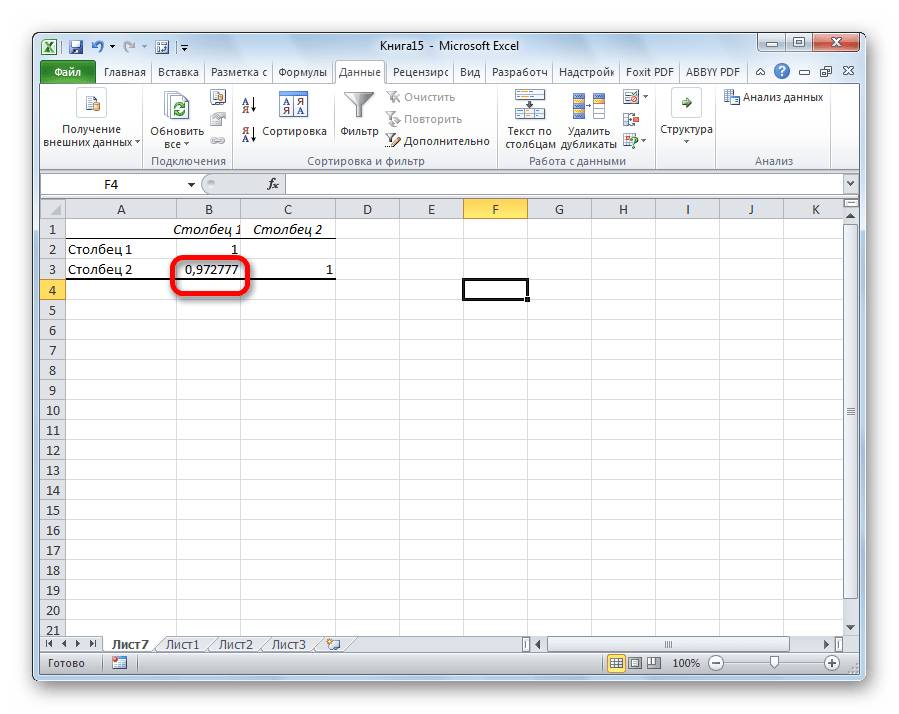
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции
(
критерий корреляции
Пирсона, англ. Pearson Product Moment correlation coefficient)
определяет степень
линейной
взаимосвязи между случайными величинами.
где Е[…] – оператор
математического ожидания
, μ и σ –
среднее
случайной величины и ее
стандартное отклонение
.
Как следует из определения, для вычисления
коэффициента корреляции
требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки
коэффициента корреляции
используется
выборочный коэффициент корреляции
r
(
еще он обозначается как
R
xy
или
r
xy
)
:
Как видно из формулы для расчета
корреляции
, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что
корреляция
оказывается безразмерным числом от -1 до 1.
Корреляция
и
ковариация
предоставляют одну и туже информацию, но
корреляцией
удобнее пользоваться, т.к. она является безразмерной величиной.
Рассчитать
коэффициент корреляции
и
ковариацию выборки
в MS EXCEL не представляет труда, так как для этого имеются специальные функции
КОРРЕЛ()
и
КОВАР()
. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.
Теоретическое отступление
Напомним, что
корреляционной связью
называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные
средние
значения другой (с изменением значения Х
среднее значение
Y изменяется закономерным образом). Предполагается, что
обе
переменные Х и Y являются
случайными
величинами и имеют некий случайный разброс относительно их
среднего значения
.
Примечание
. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о
корреляции
температуры и года наблюдения и, соответственно, применять показатели
корреляции
с соответствующей их интерпретацией.
Корреляционная связь
между переменными может возникнуть несколькими путями:
-
Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как
независимая переменная (фактор)
, вторая —
зависимая переменная (результат)
. Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот. - Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
- Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.
Таким образом,
показатель корреляции
показывает, насколько сильна
линейная взаимосвязь
между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Корреляция
, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если
диаграмма рассеяния
показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то
корреляция
замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение
коэффициента корреляции
может ввести в заблуждение (см.
файл примера
).
Корреляция
близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная
корреляция
означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
- количество переменных должно быть равно двум;
-
переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление
среднего значения
, которое требуется для нахождения
корреляции
, некорректно, а значит некорректно и вычисление самой
корреляции
; -
переменные должны быть случайными величинами и иметь
нормальное распределение
.
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
-
Для данных с нелинейной связью
корреляцию
нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования). -
С помощью
диаграммы рассеяния
у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования. - У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
- Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.
Использование MS EXCEL для расчета корреляции
В качестве примера возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х
i
; Y
i
). Для наглядности построим
диаграмму рассеяния
.
Примечание
: Подробнее о построении диаграмм см. статью
Основы построения диаграмм
. В
файле примера
для построения
диаграммы рассеяния
использована
диаграмма График
, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).
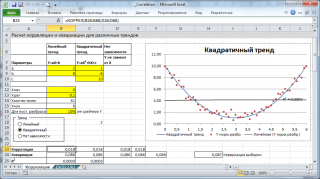
Расчеты
корреляции
проведем для различных случаев взаимосвязи между переменными:
линейной, квадратичной
и при
отсутствии связи
.
Примечание
: В
файле примера
можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
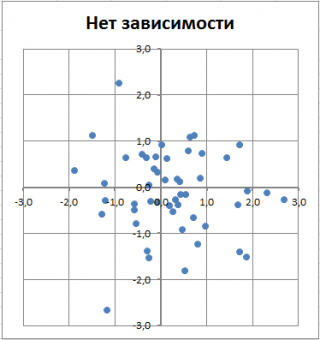
В
файле примера
для построения
диаграммы рассеяния
в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание
: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Как было сказано выше, для расчета
коэффициента корреляции
в MS EXCEL существует функций
КОРРЕЛ()
. Также можно воспользоваться аналогичной функцией
PEARSON()
, которая возвращает тот же результат.
Для того, чтобы удостовериться, что вычисления
корреляции
производятся функцией
КОРРЕЛ()
по вышеуказанным формулам, в
файле примера
приведено вычисление
корреляции
с помощью более подробных формул:
=
КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)
=
КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)
Примечание
: Квадрат
коэффициента корреляции
r равен
коэффициенту детерминации
R2, который вычисляется при построении линии регрессии с помощью функции
КВПИРСОН()
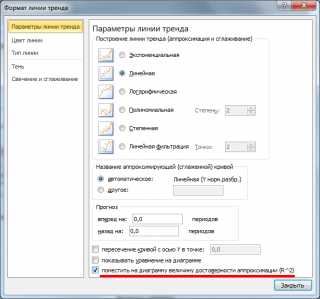
. Значение R2 также можно вывести на
диаграмме рассеяния
, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку
Макет
, затем в группе
Анализ
нажмите кнопку
Линия тренда
и выберите
Линейное приближение
). Подробнее о построении линии тренда см., например, в
статье о методе наименьших квадратов
.
Использование MS EXCEL для расчета ковариации
Ковариация
близка по смыслу с
дисперсией
(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а
дисперсия
— для одной. Поэтому, cov(x;x)=VAR(x).
Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
. В первом случае формула для вычисления аналогична вышеуказанной (окончание
.Г
обозначает
Генеральная совокупность
), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание
.В
обозначает
Выборка
.
Примечание
: Функция
КОВАР()
, которая присутствует в MS EXCEL более ранних версий, аналогична функции
КОВАРИАЦИЯ.Г()
.
Примечание
: Функции
КОРРЕЛ()
и
КОВАР()
в английской версии представлены как CORREL и COVAR. Функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета
ковариации
:
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)
Эти формулы используют свойство
ковариации
:
Если переменные
x
и
y
независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А
дисперсия
их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
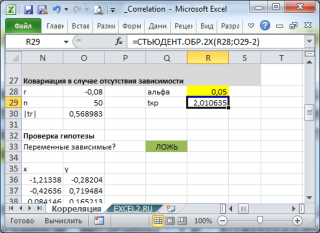
Оценка статистической значимости коэффициента корреляции
При проверке значимости
коэффициента корреляции
нулевая гипотеза состоит в том, что
коэффициент корреляции
равен нулю, альтернативная — не равен нулю (про
проверку гипотез
см. статью
Проверка гипотез
).
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.
коэффициента корреляции
r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t
r
:
которая имеет
распределение Стьюдента
с n-2 степенями свободы.
Если вычисленное значение случайной величины |t
r
| больше, чем критическое значение t
α,n-2
(α- заданный
уровень значимости
), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
Надстройка Пакет анализа
В
надстройке Пакет анализа
для вычисления ковариации и корреляции
имеются одноименные инструменты
анализа
.
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Входной интервал
: нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
Группирование
: как правило, исходные данные вводятся в 2 столбца
Метки в первой строке
: если установлена галочка, то
Входной интервал
должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
Выходной интервал
: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
-
Назначение корреляционного анализа
-
Выполняем корреляционный анализ
- Метод 1: применяем функцию КОРРЕЛ
- Метод 2: используем “Пакет анализа”
- Заключение
Назначение корреляционного анализа
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
- если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
КОРРЕЛ(массив1;массив2).
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
- Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
Correlation is a concept that hails from the statistics background. In statistical terms, correlation can be defined as the linear association between two entities. Simply, it can be understood as the change in one entity leads to how much proportion changes in another entity. Many times correlation is often confused with another popular term in statistics Causation. To differentiate and clarify, one must understand, correlation does not cause a change in values of the second entity when values of the first entity change and vice-versa.
Let’s understand this difference with help of an example. It has been often observed that during the summer season crimes rates usually increase in a city and also during the summer season there is an increase in the sale of ice cream. We can easily understand that due to the increase in temperature people tend to prefer cooler food items for relaxation from heat thus it causes an increase in ice-cream sales. Thus, this is a common cause of Causation, whereas when we compare the increase in the sale of ice cream to increase in crime rate during summer, both are correlated but one is not the cause of another.
Now, there can be either a positive correlation or a negative correlation between two entities. The degree of correlation is often given using a correlation coefficient named as Pearson Correlation coefficient which is named after Karl Pearson who gave the concept of Correlation. The statistical formula for Pearson’s coefficient is given as:
Where x and y are two separate entities, Cov(x,y) is the covariance between two entities x and y, σx and σy is the standard deviation of x and y respectively. To know more about the mathematical equation and how it is used you can refer to https://www.geeksforgeeks.org
Correlation in Excel
The value of the correlation coefficient ranges from -1 to +1. The closer the value is to -1 or +1, the strongly both entities are related to one another. If the correlation coefficient comes out to be 0, we say that there is no linear relationship between both entities. Let’s understand this with the help of an example in which we will calculate the Pearson correlation coefficient using Excel. Suppose, we have records of height and weight of 10 students of a class which is given as:
| Height (in cm) | Weight (in Kg) |
|---|---|
|
155 |
66 |
|
178 |
82 |
|
148 |
62 |
|
162 |
70 |
|
165 |
71 |
|
172 |
74 |
|
158 |
64 |
|
152 |
65 |
|
176 |
80 |
|
185 |
93 |
We can calculate correlation in Excel using two methods:
Method 1: Using CORREL() function
Excel has a built-in CORREL() function that can be used for calculating the Pearson correlation coefficient. The basic syntax for CORREL() is given as:
=CORREL(array1, array2)
Where array1 and array2 are the arrays of records of the first entity and second entity respectively.
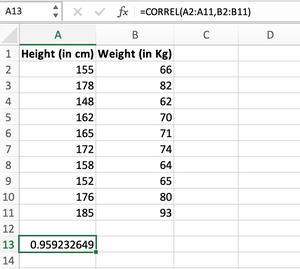
Step 1: We can calculate the Correlation coefficient between both the attributes using the formula applied in the A13 cell, i.e.,
=CORREL(A2:A11, B2:B11)
We pass the first array, Height (in cm) from A2:A11 as the first parameter, and the second array, Weight (in kg) from B2:B11 as the second parameter inside the CORREL() formula.
Using the CORREL() function to calculate Pearson’s correlation coefficient
The value obtained after calculating the correlation coefficient comes out to be 0.959232649 which is very close to +1, hence we can derive a conclusion that the height and weight of the student are highly positively correlated to each other. We can likely say if a student is taller then there are higher chances that the student will be having higher weight as well.
A video is also given below demonstrating all the usage of the CORREL() function to calculate the correlation value.
Method 2: Using the data analysis tool
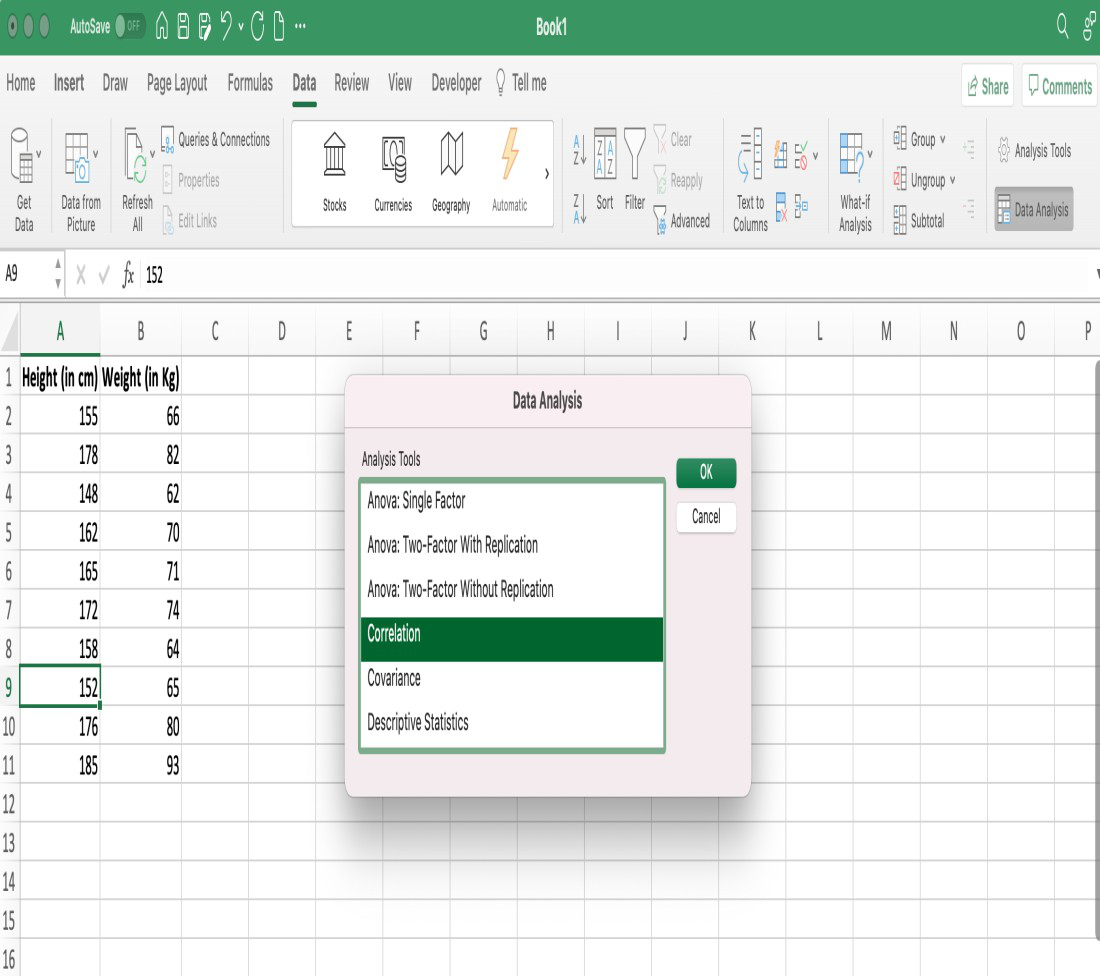
Step 1: In the menu bar, select the Data tab.
Step 2: From the data tab, select the Data Analysis option.
Step 3: A data analysis tools dialog box will appear, in the dialog box select the Correlation option.
Data Analysis dialog box
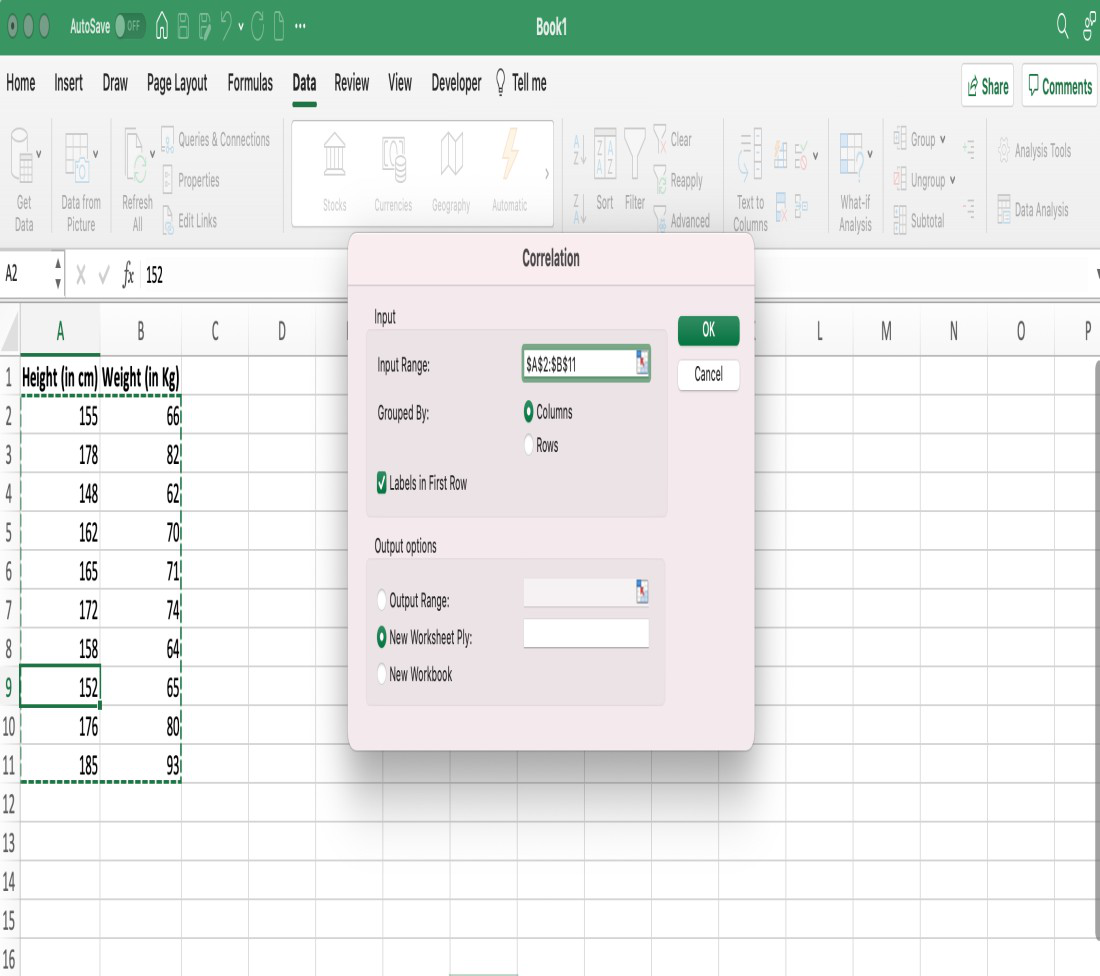
Step 4: An additional dialog box for correlation will appear, in the dialog box first we have to give the input range, so select the entire table. Since our data is grouped by Columns we will select the Columns option. Also, our data have labels in the first row, therefore we will click the checkbox saying Labels in the first row. We can get output as per our requirement in the current sheet or a new worksheet or a new workbook. We can select the new worksheet option and click the OK button.
Filling all the values inside the correlation dialog box
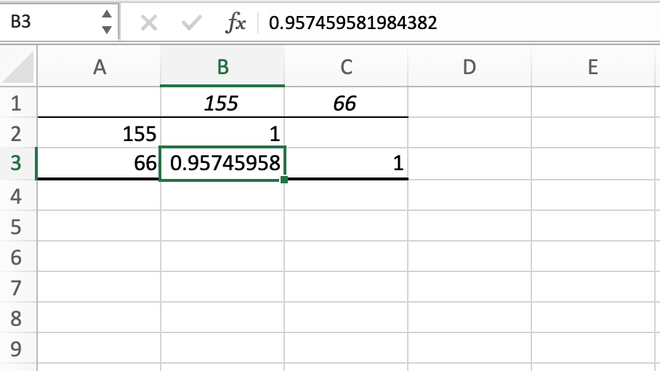
Step 5: The output will get automatically generated in the new worksheet.
Correlation table generated using the Data Analysis tool
A video is also given below demonstrating all the above steps given above to calculate the correlation value.
From the new worksheet, we can notice a correlation table will get generated in which we can see our correlation value between height and weight comes out to be 0.959232649, which we also got in using the first method.