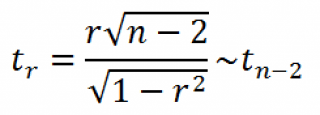Практическая
работа
Откройте на
рабочем столе файл под названием «Работники».
В данной таблице
представлен список работников с указанием стажа работы до приёма на эту работу
и после приёма, а также указана заработная плата.
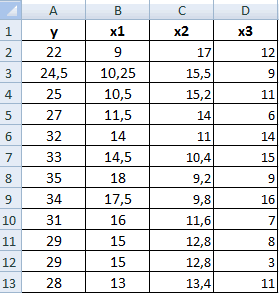
Задание 1. Заполнить
столбец Общий стаж работы. Для этого в ячейку F2 необходимо
ввести формулу =D2+E2, затем
скопировать формулу методом протаскивания сверху вниз, для того чтобы
просчитать общий стаж по всем ячейкам данного столбца. В итоге для каждого сотрудника
должен быть рассчитан общий стаж.
Задание 2.
Рассчитать
максимальную зарплату. В ячейку G11 ввести
формулу = МАКС(G2:G10). В
результате в ячейке должна быть отражена максимальная зарплата.
Задание 3.
Рассчитать
минимальную зарплату. В ячейку G12 ввести
формулу = МИН(G2:G10). В
результате в ячейке должна быть отражена минимальная зарплата.
Задание 4.
Рассчитать
среднее количество лет стажа работников по трём столбца: D, E, F. Для
этого в ячейку D13 введите
формулу =СРЗНАЧ(D2:D9), методом
протаскивания слева направо скопируйте формулу в ячейки E13, F13.
Задание 5.
Рассчитать
максимальное количество лет по трём столбца: D, E, F. Для
этого в ячейку D14 введите
формулу =МАКС(D2:D9), методом
протаскивания слева направо скопируйте формулу в ячейки E14, F14.
Задание 6.
Рассчитать
минимальное количество лет по трём столбца: D, E, F. Для
этого в ячейку D15 введите
формулу =МИН(D2:D9), методом
протаскивания слева направо скопируйте формулу в ячейки E15, F15.
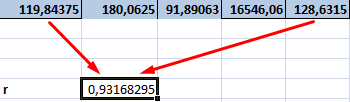
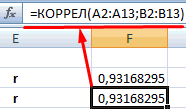
Задание 7.
Рассчитать
корреляционную зависимость. Зависимость заработной платы от общего стажа
работников.
Для этого в ячейку
C16 введите
формулу = КОРРЕЛ(F2:F9;G2:G9).
Задание 8.
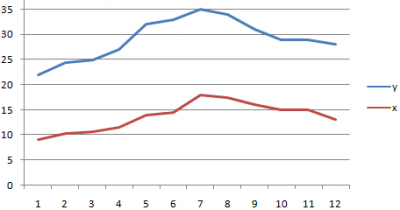
Постройте
точечную диаграмму.
Выделите
количественные данные в столбцах F и G нажмите вставка-
диаграмма- точечная. Добавьте названия осей
Задание 9.
Добавьте
линейную линию тренда. Диаграмма – добавить линию тренда – тип — линейная
Задание
10. Добавьте
ещё 3 столбца по образцу
Посчитайте
сколько сотрудников должно быть и вставьте количество по столбцам
Посчитаёте сколько
процентов приходится для каждого критерия
Для этого в ячейку
H3 введите
формулу =H2/9. Методом
протаскивания скопируйте её в ячейки I3, J3.
Выделите
полученные три числа и поменяйте тип данных на процентный.
Должно получиться
так
Задание
11. Постройте диаграмму для последнего результата.
Выделите
полученный диапазон ячеек. Нажмите вставка – диаграмма – круговая – объёмная –
добавить
4
ЛАБОРАТОРНАЯ РАБОТА
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В EXCEL
1.1 Корреляционный анализ в MS Excel
Корреляционный анализ состоит в
определении степени связи между двумя
случайными величинами X и Y. В качестве
меры такой связи используется коэффициент
корреляции. Коэффициент корреляции
оценивается по выборке объема п связанных
пар наблюдений (xi, yi) из
совместной генеральной совокупности
X и Y. Для оценки степени взаимосвязи
величин X и Y, измеренных в количественных
шкалах, используется коэффициент
линейной корреляции (коэффициент
Пирсона), предполагающий, что выборки
X и Y распределены по нормальному закону.
Коэффициент корреляции изменяется от
-1 (строгая обратная линейная зависимость)
до 1 (строгая прямая пропорциональная
зависимость). При значении 0 линейной
зависимости между двумя выборками
нет.
Общая классификация корреляционных
связей (по Ивантер Э.В., Коросову А.В.,
1992):
-
сильная,
или тесная
при коэффициенте корреляции r0,70;
-
средняя при
0,50r
0,69;
-
умеренная при
0,30r
0,49;
-
слабая при
0,20r
0,29;
-
очень слабая при r
0,19.
Существует несколько типов
коэффициентов корреляции, что зависит
от переменных Х и Y,
которые могут быть измерены в разных
шкалах. Именно этот факт и определяет
выбор соответствующего коэффициента
корреляции (см. табл. 13):
В MS Excel для вычисления парных коэффициентов
линейной корреляции используется
специальная функция КОРРЕЛ (массив1;
массив2),
|
№ испытуемых |
X |
Y |
|
1 |
19 |
17 |
|
2 |
32 |
7 |
|
3 |
33 |
17 |
|
4 |
44 |
28 |
|
5 |
28 |
27 |
|
6 |
35 |
31 |
|
7 |
39 |
20 |
|
8 |
39 |
17 |
|
9 |
44 |
35 |
|
10 |
44 |
43 |
где массив1 – ссылка на диапазон
ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек
второй выборки (Y).
Пример 1: 10 школьникам были даны
тесты на наглядно-образное и вербальное
мышление. Измерялось среднее время
решения заданий теста в секундах.
Исследователя интересует вопрос:
существует ли взаимосвязь между
временем решения этих задач? Переменная
X — обозначает среднее время решения
наглядно-образных, а переменная Y—
среднее время решения вербальных
заданий тестов.
Р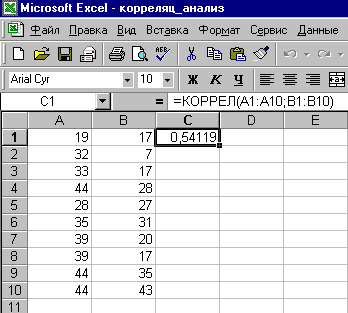
Для выявления степени взаимосвязи,
прежде всего, необходимо ввести данные
в таблицу MS Excel (см. табл., рис. 1). Затем
вычисляется значение коэффициента
корреляции. Для этого курсор установите
в ячейку C1. На панели инструментов
нажмите кнопку Вставка функции (fx).
В появившемся диалоговом окне Мастер
функций выберите категорию
Статистические и функцию КОРРЕЛ,
после чего нажмите кнопку ОК. Указателем
мыши введите диапазон данных выборки
Х в поле массив1 (А1:А10). В поле массив2
введите диапазон данных выборки У
(В1:В10). Нажмите кнопку ОК. В ячейке С1
появится значение коэффициента
корреляции — 0,54119. Далее необходимо
посмотреть на абсолютное число
коэффициента корреляции и определить
тип связи (тесная, слабая, средняя и
т.д.)
Рис. 1. Результаты вычисления коэффициента
корреляции
Таким образом, связь между
временем решения наглядно-образных и
вербальных заданий теста не доказана.
Задание 1. Имеются данные по 20
сельскохозяйственным хозяйствам. Найти
коэффициент корреляции между
величинами урожайности зерновых культур
и качеством земли и оценить его значимость.
Данные приведены в таблице.
Таблица 2. Зависимость урожайности
зерновых культур от качества земли
|
Номер |
Качество |
Урожайность, |
|
1 |
32 |
19,5 |
|
2 |
33 |
19 |
|
3 |
35 |
20,5 |
|
4 |
37 |
21 |
|
5 |
38 |
20,8 |
|
6 |
39 |
21,4 |
|
7 |
40 |
23 |
|
8 |
41 |
23,3 |
|
9 |
42 |
24 |
|
10 |
44 |
24,5 |
|
11 |
45 |
24,2 |
|
12 |
46 |
25 |
|
13 |
47 |
27 |
|
14 |
49 |
26,8 |
|
15 |
50 |
27,2 |
|
16 |
52 |
28 |
|
17 |
54 |
30 |
|
18 |
55 |
30,2 |
|
19 |
58 |
32 |
|
20 |
60 |
33 |
Задание 2. Определите,
имеется ли связь между временем работы
спортивного тренажера для фитнеса (тыс.
часов) и стоимость его ремонта (тыс.
руб.):
-
Время
работа тренажера (тыс. часов)Стоимость
ремонта (тыс. руб.)0,50
7,50
0,60
7,75
0,70
7,25
0,80
7,40
0,90
7,90
1,00
8,00
1,10
8,50
1,20
8,40
1,30
8,35
1,40
8,55
1,50
8,70
1,60
9,05
1,70
8,80
1,80
9,10
1,90
9,30
2,00
9,25
2,10
9,45
1.2
Множественная корреляция в MS Excel
При большом числе наблюдений,
когда коэффициенты корреляции необходимо
последовательно вычислять для нескольких
выборок, для удобства получаемые
коэффициенты сводят в таблицы, называемые
корреляционными
матрицами.
Корреляционная матрица — это
квадратная таблица, в которой на
пересечении соответствующих строк и
столбцов находятся коэффициент корреляции
между соответствующими параметрами.
В MS Excel для вычисления
корреляционных матриц используется
процедура Корреляция
из пакета Анализ
данных. Процедура
позволяет получить корреляционную
матрицу, содержащую коэффициенты
корреляции между различными параметрами.
Для реализации процедуры необходимо:
1. выполнить команду Сервис
— Анализ
данных;
2. в появившемся списке
Инструменты анализа
выбрать строку Корреляция
и нажать кнопку ОК;
3. в появившемся диалоговом
окне указать Входной
интервал, то есть
ввести ссылку на ячейки, содержащие
анализируемые данные. Входной интервал
должен содержать не менее двух столбцов.
4. в разделе Группировка
переключатель установить в соответствии
с введенными данными (по столбцам или
по строкам);
5. указать выходной
интервал,
то есть ввести ссылку на ячейку, начиная
с которой будут показаны результаты
анализа. Размер выходного диапазона
будет определен автоматически, и на
экран будет выведено сообщение в случае
возможного наложения выходного диапазона
на исходные данные. Нажать кнопку ОК.
В
выходной диапазон будет выведена
корреляционная матрица, в которой
на пересечении каждых строки и столбца
находится коэффициент корреляции
между соответствующими параметрами.
Ячейки выходного диапазона, имеющие
совпадающие координаты строк и столбцов,
содержат значение 1, так как каждый
столбец во входном диапазоне полностью
коррелирует сам с собой
Пример 2.
Имеются ежемесячные данные наблюдений
за состоянием погоды и посещаемостью
музеев и парков (см. табл. 3). Необходимо
определить, существует ли взаимосвязь
между состоянием погоды и посещаемостью
музеев и парков.
Таблица 3. Результаты наблюдений
-
Число
ясных днейКоличество
посетителей музеяКоличество
посетителей парка8
495
132
14
503
348
20
380
643
25
305
865
20
348
743
15
465
541
Решение.
Для выполнения корреляционного анализа
введите в диапазон A1:G3 исходные данные
(рис. 2). Затем в меню Сервис
выберите пункт Анализ
данных
и далее укажите строку Корреляция.
В появившемся диалоговом окне укажите
Входной интервал
(А2:С7). Укажите, что данные рассматриваются
по столбцам. Укажите выходной диапазон
(Е1) и нажмите кнопку ОК.
На рис. 33 видно, что корреляция
между состоянием погоды и посещаемостью
музея равна -0,92, а между состоянием
погоды и посещаемостью парка — 0,97,
между посещаемостью парка и музея —
0,92.
Таким образом, в результате
анализа выявлены зависимости: сильная
степень обратной линейной взаимосвязи
между посещаемостью музея и количеством
солнечных дней и практически линейная
(очень сильная прямая) связь между
посещаемостью парка и состоянием погоды.
Между посещаемостью музея и парка
имеется сильная обратная взаимосвязь.
Рис. 2. Результаты вычисления
корреляционной матрицы из примера 2
Задание 3. 10 менеджеров
оценивались по методике экспертных
оценок психологических характеристик
личности руководителя. 15 экспертов
производили оценку каждой психологической
характеристики по пятибальной системе
(см. табл. 4). Психолога интересует вопрос,
в какой взаимосвязи находятся эти
характеристики руководителя между
собой.
Таблица 4. Результаты исследования
|
Испытуемые п/п |
тактичность |
требовательность |
критичность |
|
1 |
70 |
18 |
36 |
|
2 |
60 |
17 |
29 |
|
3 |
70 |
22 |
40 |
|
4 |
46 |
10 |
12 |
|
5 |
58 |
16 |
31 |
|
6 |
69 |
18 |
32 |
|
7 |
32 |
9 |
13 |
|
8 |
62 |
18 |
35 |
|
9 |
46 |
15 |
30 |
|
10 |
62 |
22 |
36 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Практическая работа №17
«Расчет корреляционных зависимостей в Microsoft Excel»
Тип урока: практическая работа
Цели:
Получение представления о корреляционной зависимости величин;
Освоение способа вычисления коэффициента корреляции с помощью функции КОРРЕЛ;
Формирование навыка по работе в MS Excel;
Развитие системного мышления, позволяющего выделять в окружающей действительности системы, элементы систем, адекватные поставленной задаче;
Формирование профессиональных навыков работы.
Оборудование:
ПК;
Интерактивная доска;
MS Excel
Ход урока:
I. Организационный момент (5 мин.)
Приветствие. Сообщение темы.
II. Актуализация знаний (5 мин.)
Проверка домашнего задания.
III. Практическая работа (30 мин.)
Практическая работа №17
Задание 1
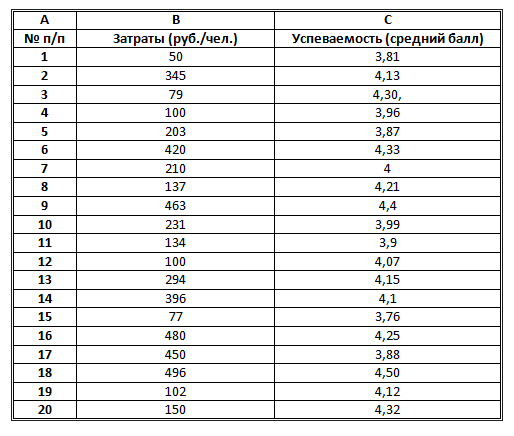
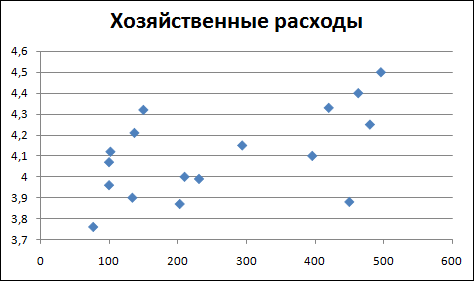
Требуется выполнить расчеты корреляционной зависимости успеваемости учащихся от хозяйственных расходов школы, описанные в § 38 учебника.
1. Заполнить электронную таблицу следующими данными:
|
А |
В |
С |
|
№ п/п |
Затраты (руб./чел.) |
Успеваемость (средний балл) |
|
1 |
50 |
3,81 |
|
2 |
345 |
4,13 |
|
3 |
79 |
4,30 |
|
4 |
100 |
3,96 |
|
5 |
203 |
3,87 |
|
6 |
420 |
4,33 |
|
7 |
210 |
4 |
|
8 |
137 |
4,21 |
|
9 |
463 |
4,4 |
|
10 |
231 |
3,99 |
|
11 |
134 |
3,9 |
|
12 |
100 |
4,07 |
|
18 |
294 |
4,15 |
|
14 |
396 |
4,1 |
|
15 |
77 |
3,76 |
|
16 |
480 |
4,25 |
|
17 |
450 |
3,88 |
|
18 |
496 |
4,50 |
|
19 |
102 |
4,12 |
|
20 |
150 |
4,32 |
2. Построить точечную диаграмму зависимости величин (ее вид показан в учебнике на рис. 6.7).
3. Выполнить статистическую функцию КОРРЕЛ, указав в диалоговом окне диапазоны значений: В2:В21 и С2:С21.
4. Выписать значение коэффициента корреляции.
Задание 2
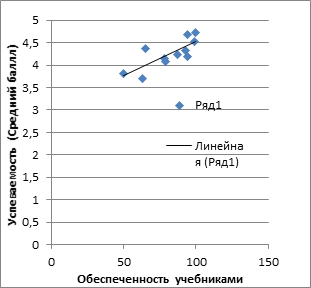
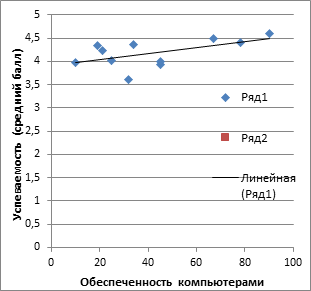
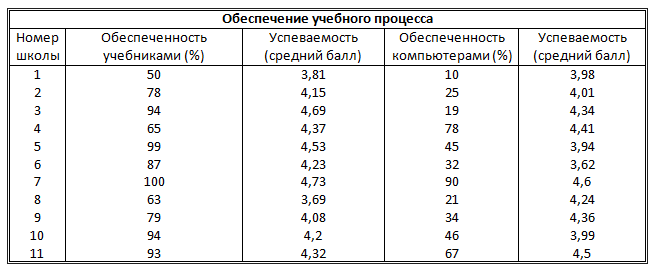
Выполнить расчеты корреляционных зависимостей успеваемости учащихся от обеспеченности учебниками и от обеспеченности компьютерами, представленными в следующей таблице.
|
Обеспечение учебного процесса |
||||
|
Номер школы |
Обеспеченность учебниками (%) |
Успеваемость (средний балл) |
Обеспеченность компьютерами (%) |
Успеваемость (средний балл) |
|
1 |
50 |
3,81 |
10 |
3,98 |
|
2 |
78 |
4,15 |
25 |
4,01 |
|
3 |
94 |
4,69 |
19 |
4,34 |
|
4 |
65 |
4,37 |
78 |
4,41 |
|
5 |
99 |
4,53 |
45 |
3,94 |
|
6 |
87 |
4,23 |
32 |
3,62 |
|
7 |
100 |
4,73 |
90 |
4,6 |
|
8 |
63 |
3,69 |
21 |
4,24 |
|
9 |
79 |
4,08 |
34 |
4,36 |
|
10 |
94 |
4,2 |
45 |
3,99 |
|
11 |
93 |
4,32 |
67 |
4,5 |
Полученные значения коэффициентов корреляции сопоставить с приведенными в § 38 учебника.
Задание для самостоятельного выполнения по теме
«Корреляционные зависимости»
Придумать таблицу парных измерений значений некоторых величин, между которыми существует гипотетическая корреляционная зависимость. Провести анализ этой зависимости на наличие линейной корреляции.
Примерами соответствующих связанных величин могут служить:
уровень образования (измеренный, например, в годах обучения в целом) и уровень месячного дохода;
уровень образования и уровень занимаемой должности (для последней придумайте условную шкалу);
количество компьютеров в школе, приходящихся на одного учащегося, и средняя оценка при тестировании на уровень владения стандартными технологиями обработки информации;
количество часов, затрачиваемых старшеклассниками на выполнение домашних заданий, и средняя оценка;
количество удобрений, вносимых в почву, и урожайность той или иной сельскохозяйственной культуры.
При этом вы можете идти двумя путями. Первый, более серьезный и практически полезный: вы не просто придумываете гипотетическую корреляционную зависимость, но и находите в литературе действительные данные о ней. Второй путь, более легкий: вы рассматриваете это как игру, необходимую для понимания того, что такое корреляционная зависимость, и выработки технических навыков ее анализа, и придумываете соответствующие данные, стараясь делать это наиболее правдоподобным образом.
IV. Итог урока (2 мин.) Объявляются оценки.
V. Домашнее задание (3 мин.) Повторить § 38
Тема: Практическая работа
«Расчет корреляционных зависимостей в Microsoft Excel»
Выполнить расчеты корреляционных зависимостей успеваемости
учащихся от обеспеченности учебниками и от обеспеченности
компьютерами, представленными в следующей таблице.
1.
Заполнить электронную таблицу следующими данными:
|
Номер |
Обеспеченность |
Успеваемость |
Обеспеченность |
Успеваемость |
|
1 |
50 |
3,81 |
10 |
3,98 |
|
2 |
78 |
4,15 |
25 |
4,01 |
|
3 |
94 |
4,69 |
19 |
4,34 |
|
4 |
65 |
4,37 |
78 |
4,41 |
|
5 |
99 |
4,53 |
45 |
3,94 |
|
6 |
87 |
4,23 |
32 |
3,62 |
|
7 |
100 |
4,73 |
90 |
4,60 |
|
8 |
63 |
3,69 |
21 |
4,24 |
|
9 |
79 |
4,08 |
34 |
4,36 |
|
10 |
94 |
4,2 |
45 |
3,99 |
|
11 |
93 |
4,32 |
67 |
4,50 |
|
Корреляция |
=КОРРЕЛ(B2:B12;C2:C12) |
Корреляция |
=КОРРЕЛ(D2:D12;E2:E12) |
2.
Построить точечную диаграмму зависимости величин.
3.
Добавить названия осей
по наименованию столбцов, используя команду Макет меню Главная
.
4.
Выполнить статистическую функцию КОРРЕЛ, указав в диалоговом окне
диапазоны значений:
— Обеспеченность учебниками (%),Успеваемость
(средний балл) — Корреляция -учебники;
— Обеспеченность
компьютерами (%),Успеваемость (средний балл) — Корреляция –компьютеры.
5. Выписать
и пояснить значения коэффициентов корреляции.
Подборка по базе: дипломная работа.docx, практ работа +++.doc, Практическая работа №1.docx, Курсовая работа похищение человека.docx, Практическая работа №1.docx, Самостоятельная работа по теме 1.2.docx, Контрольная Работа.. (пп).docx, Практическая работа по Теории организации Марчук ЮП.docx, практическая работа №6 ответ.docx, Лабораторная работа по биологии_ Определение по спилу возраста п
ЛАБОРАТОРНАЯ РАБОТА
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В EXCEL
1.1 Корреляционный анализ в MS Excel
Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (xi, yi) из совместной генеральной совокупности X и Y. Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону.
Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет.
Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):
Существует несколько типов коэффициентов корреляции, что зависит от переменных Х и Y, которые могут быть измерены в разных шкалах. Именно этот факт и определяет выбор соответствующего коэффициента корреляции (см. табл. 13):
В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ (массив1; массив2),
| № испытуемых | X | Y |
| 1 | 19 | 17 |
| 2 | 32 | 7 |
| 3 | 33 | 17 |
| 4 | 44 | 28 |
| 5 | 28 | 27 |
| 6 | 35 | 31 |
| 7 | 39 | 20 |
| 8 | 39 | 17 |
| 9 | 44 | 35 |
| 10 | 44 | 43 |
где массив1 – ссылка на диапазон ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек второй выборки (Y).
Пример 1: 10 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов.
Р
В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Указателем мыши введите диапазон данных выборки Х в поле массив1 (А1:А10). В поле массив2 введите диапазон данных выборки У (В1:В10). Нажмите кнопку ОК. В ячейке С1 появится значение коэффициента корреляции — 0,54119. Далее необходимо посмотреть на абсолютное число коэффициента корреляции и определить тип связи (тесная, слабая, средняя и т.д.)
Рис. 1. Результаты вычисления коэффициента корреляции
Таким образом, связь между временем решения наглядно-образных и вербальных заданий теста не доказана.
Задание 1. Имеются данные по 20 сельскохозяйственным хозяйствам. Найти коэффициент корреляции между величинами урожайности зерновых культур и качеством земли и оценить его значимость. Данные приведены в таблице.
Таблица 2. Зависимость урожайности зерновых культур от качества земли
| Номер хозяйства | Качество земли, балл | Урожайность, ц/га |
| 1 | 32 | 19,5 |
| 2 | 33 | 19 |
| 3 | 35 | 20,5 |
| 4 | 37 | 21 |
| 5 | 38 | 20,8 |
| 6 | 39 | 21,4 |
| 7 | 40 | 23 |
| 8 | 41 | 23,3 |
| 9 | 42 | 24 |
| 10 | 44 | 24,5 |
| 11 | 45 | 24,2 |
| 12 | 46 | 25 |
| 13 | 47 | 27 |
| 14 | 49 | 26,8 |
| 15 | 50 | 27,2 |
| 16 | 52 | 28 |
| 17 | 54 | 30 |
| 18 | 55 | 30,2 |
| 19 | 58 | 32 |
| 20 | 60 | 33 |
Задание 2. Определите, имеется ли связь между временем работы спортивного тренажера для фитнеса (тыс. часов) и стоимость его ремонта (тыс. руб.):
-
Время работа тренажера (тыс. часов) Стоимость ремонта (тыс. руб.) 0,50 7,50 0,60 7,75 0,70 7,25 0,80 7,40 0,90 7,90 1,00 8,00 1,10 8,50 1,20 8,40 1,30 8,35 1,40 8,55 1,50 8,70 1,60 9,05 1,70 8,80 1,80 9,10 1,90 9,30 2,00 9,25 2,10 9,45
1.2 Множественная корреляция в MS Excel
При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.
Корреляционная матрица — это квадратная таблица, в которой на пересечении соответствующих строк и столбцов находятся коэффициент корреляции между соответствующими параметрами.
В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.
Для реализации процедуры необходимо:
1. выполнить команду Сервис_-_Анализ_данных_;2._в_появившемся_списке_Инструменты_анализа’>Сервис — Анализ данных;
2. в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК;
3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов.
4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам);
5. указать выходной интервал, то есть ввести ссылку на ячейку, начиная с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.
В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой
Пример 2. Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков (см. табл. 3). Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.
Таблица 3. Результаты наблюдений
-
Число ясных дней Количество посетителей музея Количество посетителей парка 8 495 132 14 503 348 20 380 643 25 305 865 20 348 743 15 465 541
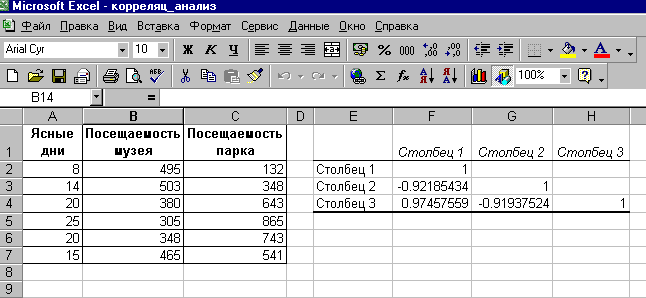
Решение. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные (рис. 2). Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.
На рис. 33 видно, что корреляция между состоянием погоды и посещаемостью музея равна -0,92, а между состоянием погоды и посещаемостью парка — 0,97, между посещаемостью парка и музея — 0,92.
Таким образом, в результате анализа выявлены зависимости: сильная степень обратной линейной взаимосвязи между посещаемостью музея и количеством солнечных дней и практически линейная (очень сильная прямая) связь между посещаемостью парка и состоянием погоды. Между посещаемостью музея и парка имеется сильная обратная взаимосвязь.
Рис. 2. Результаты вычисления корреляционной матрицы из примера 2
Задание 3. 10 менеджеров оценивались по методике экспертных оценок психологических характеристик личности руководителя. 15 экспертов производили оценку каждой психологической характеристики по пятибальной системе (см. табл. 4). Психолога интересует вопрос, в какой взаимосвязи находятся эти характеристики руководителя между собой.
Таблица 4. Результаты исследования
| Испытуемые п/п | тактичность | требовательность | критичность |
| 1 | 70 | 18 | 36 |
| 2 | 60 | 17 | 29 |
| 3 | 70 | 22 | 40 |
| 4 | 46 | 10 | 12 |
| 5 | 58 | 16 | 31 |
| 6 | 69 | 18 | 32 |
| 7 | 32 | 9 | 13 |
| 8 | 62 | 18 | 35 |
| 9 | 46 | 15 | 30 |
| 10 | 62 | 22 | 36 |
Практическая работа 3.18-ИКТ-11кл-Семакин.И.Г. (2017-02-21 )
№ 3.18 РАСЧЕТ КОРРЕЛЯЦИОННЫХ ЗАВИСИМОСТЕЙ В MS EXCEL
Цель работы: получение представления о корреляционной зависимости величин; освоение способа вычисления коэффициента корреляции с помощью функции KOPPEЛ.
Используемое программное обеспечение: табличный процессор Microsoft Office Excel.
Задание 1
Требуется выполнить расчеты корреляционной зависимости успеваемости учащихся от хозяйственных расходов школы, описанные в § 38 учебника.
1. Заполнить электронную таблицу следующими данными:
2. Построить точечную диаграмму зависимости величин.
3. Выполнить статистическую функцию KOPPEЛ, указав в диалоговом окне диапазоны значений: В2:В21 и С2:С21.
4. Выписать значение коэффициента корреляции.
Задание 2
Выполнить расчеты корреляционных зависимостей успеваемости учащихся от обеспеченности учебниками и от обеспеченности компьютерами, представленными в следующей таблице.
Задание для самостоятельного выполнения по теме «Корреляционные зависимости»
Придумать таблицу парных измерений значений некоторых величин, между которыми существует гипотетическая корреляционная зависимость. Провести анализ этой зависимости на наличие линейной корреляции.
- Примерами соответствующих связанных величин могут служить:
- • уровень образования (измеренный, например, в годах обучения в целом) и уровень месячного дохода;
- • уровень образования и уровень занимаемой должности (для последней придумайте условную шкалу);
- • количество компьютеров в школе, приходящихся на одного учащегося, и средняя оценка при тестировании па уровень владения стандартными технологиями обработки информации;
- • количество часов, затрачиваемых старшеклассниками на выполнение домашних заданий, и средняя оценка;
- • количество удобрений, вносимых в почву, и урожайность той или иной сельскохозяйственной культуры.
При этом вы можете идти двумя путями. Первый, более серьезный и практически полезный: вы не просто придумываете гипотетическую корреляционную зависимость, но и находите в литературе действительные данные о ней. Второй путь, более легкий: вы рассматриваете это как игру, необходимую для понимания того, что такое корреляционная зависимость, и выработки технических навыков ее анализа, и придумываете соответствующие данные, стараясь делать это наиболее правдоподобным образом.
Коррелляционное моделирование. Практическая работа
27.01.2020 21:04
Практическая работа по теме: «Моделирование корреляционных зависимостей» (11 класс).
Архив содержит: Файл Word с практической работой и Файл Excel с данными и результатами практической работы
Просмотр содержимого документа
«ПР Моделирование корреляционной зависимости»
Практическая работа
Тема: «Моделирование корреляционных зависимостей» (11 класс)
Цель: с помощью электронных таблиц Excel научиться:
-
строить график регрессионной модели;
-
определять наиболее удачную регрессионную модель, используя коэффициент детерминированности,
Ход работы:
-
Соберите данные о средней дневной температуре вашего села (см. Дневник погоды для школьников на https://www.gismeteo.ru/diary/182588/2017/3/).
-
Постройте таблицу данных в ЭТ Excel.
-
Постройте точечную диаграмму температур.
-
Проверьте настройки горизонтальной оси (рис. 1)
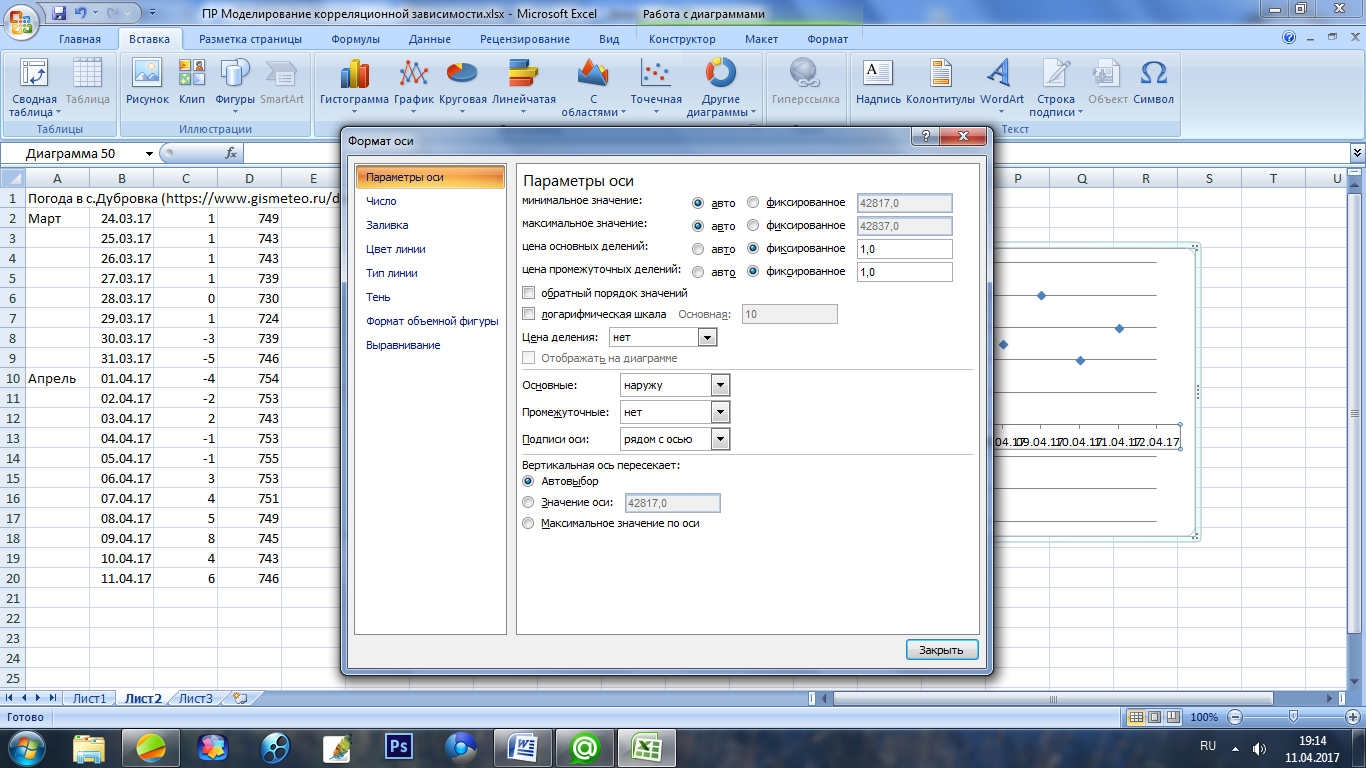

Рис.1. Формат оси (горизонтальной)
-
Аналогично установите настройки вертикальной оси: цена основных и промежуточных делений – 1.
-
Добавьте основные линии сетки, если их нет.
-
Анализируя коэффициент детерминированности, подберите наиболее удачную регрессионную модель (линию тренда).
-
Попробуйте путем графической экстраполяции предсказать температуру через 2-5 дней.
Данные для работы:
|
Месяц |
Дата |
Температура |
|
Март |
24.03.17 |
1 |
|
25.03.17 |
1 |
|
|
26.03.17 |
1 |
|
|
27.03.17 |
1 |
|
|
28.03.17 |
0 |
|
|
29.03.17 |
1 |
|
|
30.03.17 |
-3 |
|
|
31.03.17 |
-5 |
|
|
Апрель |
01.04.17 |
-4 |
|
02.04.17 |
-2 |
|
|
03.04.17 |
2 |
|
|
04.04.17 |
-1 |
|
|
05.04.17 |
-1 |
|
|
06.04.17 |
3 |
|
|
07.04.17 |
4 |
|
|
08.04.17 |
5 |
|
|
09.04.17 |
8 |
|
|
10.04.17 |
4 |
|
|
11.04.17 |
6 |
Оглавление:
- 1 Корреляционный анализ в Excel. Пример выполнения корреляционного анализа — Разбираем подробно
- 2 Суть корреляционного анализа
- 3 Назначение корреляционного анализа
- 4 Расчет коэффициента корреляции
- 4.1 Способ 1: определение корреляции через Мастер функций
- 4.2 Способ 2: вычисление корреляции с помощью Пакета анализа
- 5 Определение и вычисление множественного коэффициента корреляции в MS Excel
- 6 Коэффициент парной корреляции в Excel
- 6.1 Расчет коэффициента парной корреляции в Excel
- 6.2 Матрица парных коэффициентов корреляции в Excel
- 7 Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- 7.1 Примеры использования функции КОРРЕЛ в Excel
- 7.2 Определение коэффициента корреляции влияния действий на результат
- 7.3 Анализ популярности контента по корреляции просмотров и репостов видео
- 7.4 Особенности использования функции КОРРЕЛ в Excel
- 8 Оценка статистической значимости коэффициента корреляции
- 9 Заключение
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
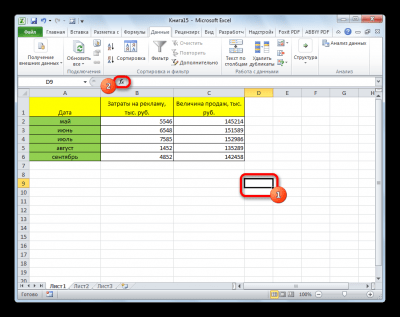
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
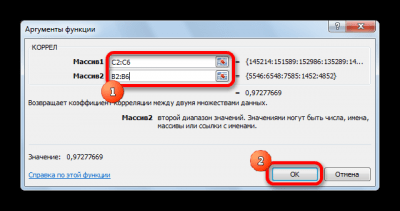
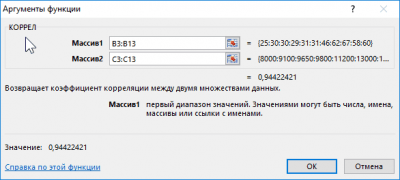
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид – КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
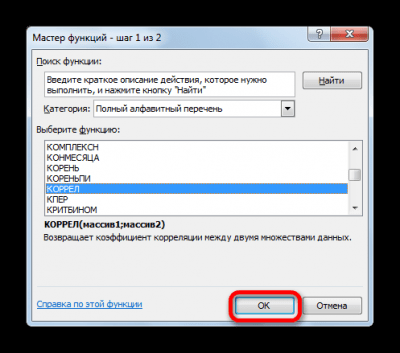
1
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
2
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
3
- После введения всех диапазонов кликаем на кнопку «ОК».
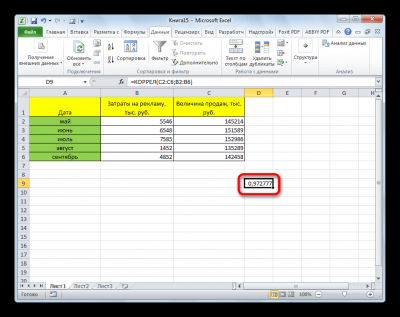
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
4
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
5
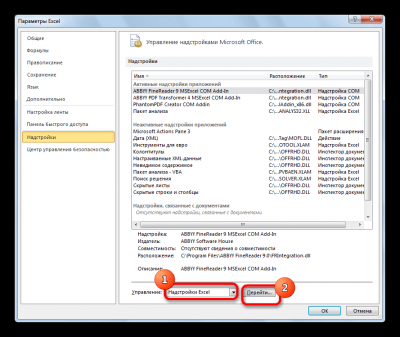
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
6
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
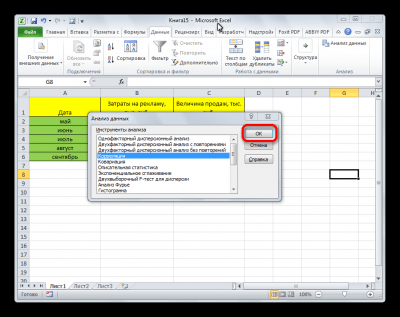
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
7
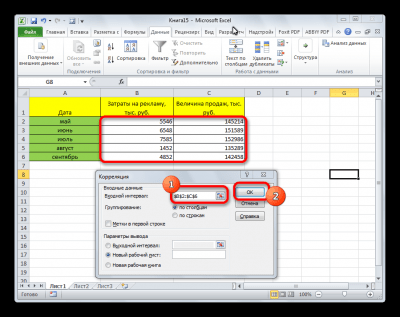
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
8
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
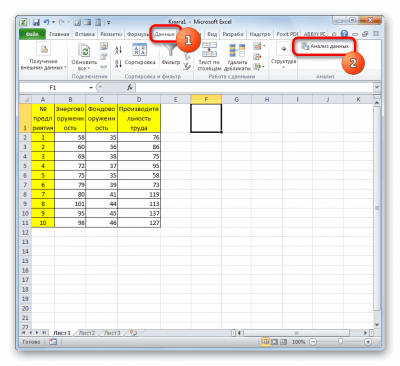
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
9
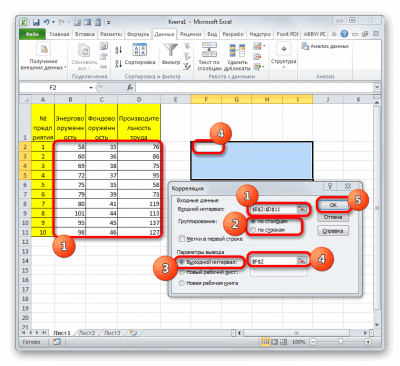
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
10
- Готово! Построилась матрица корреляции.
11
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
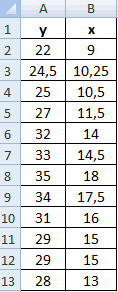
К примеру, у вас есть значения величин х и у.
12
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
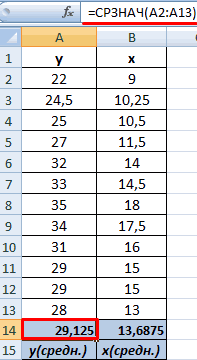
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
13
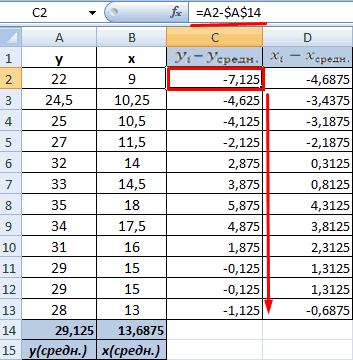
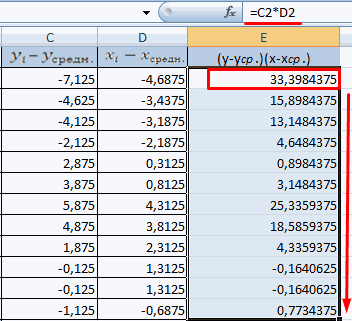
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
14
- Производим перемножение вычисленных разностей.
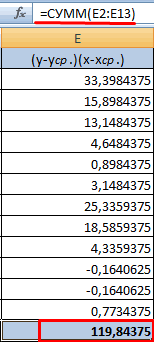
15
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
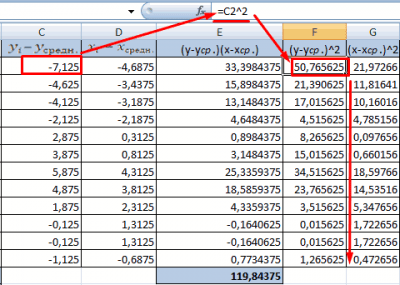
16
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
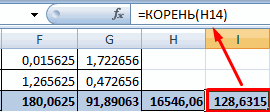
17
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
18
- Производим подсчет частного, используя значения знаменателя и числителя.
19
20
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
21
Матрица парных коэффициентов корреляции в Excel
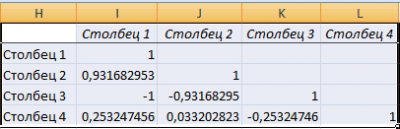
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
22
Пошаговая инструкция:
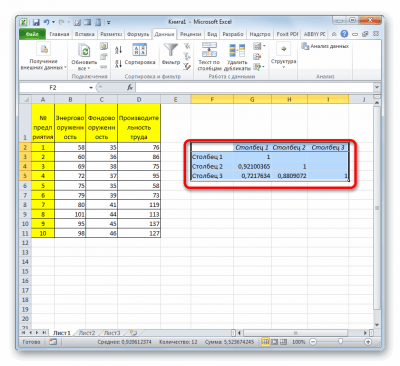
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
23
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
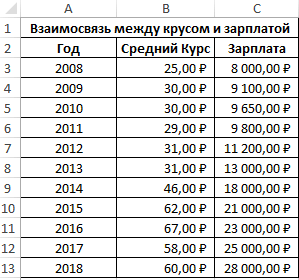
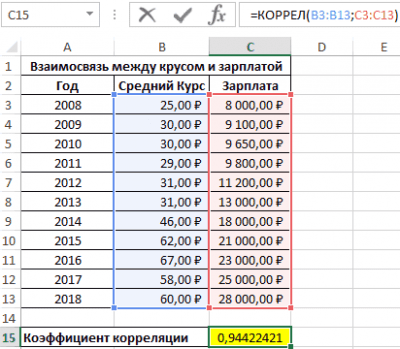
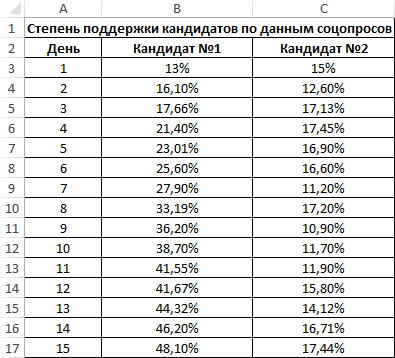
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
24
Алгоритм расчёта выглядит следующим образом:
25
Отображенный показатель близок к 1. Результат:
26
Определение коэффициента корреляции влияния действий на результат
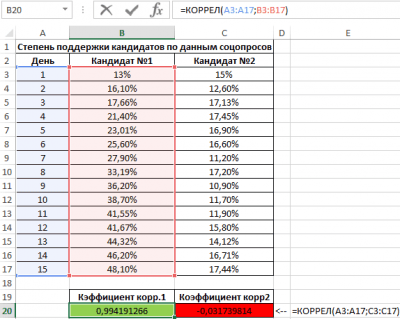
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
27
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
Результаты:
28
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
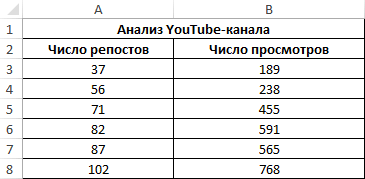
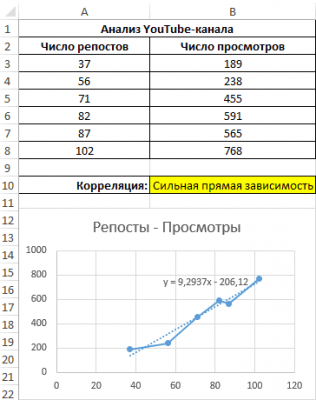
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
29
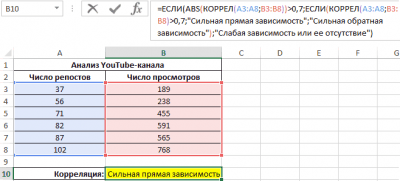
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
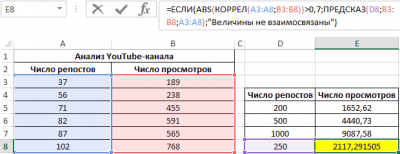
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;”Сильная прямая зависимость”;”Сильная обратная зависимость”);”Слабая зависимость или ее отсутствие”)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
30
Теперь производим построение графика:
31
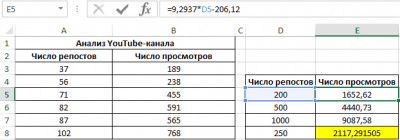
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
32
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);”Величины не взаимосвязаны”)’ class=’formula’>. Получаем следующие результаты:
33
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «–» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
34
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Did you find apk for android? You can find new Free Android Games and apps.