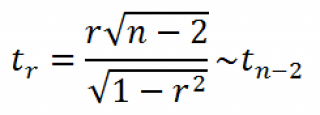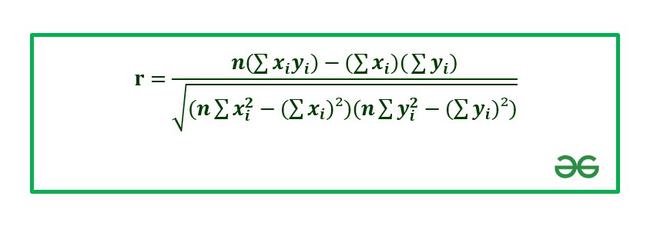Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
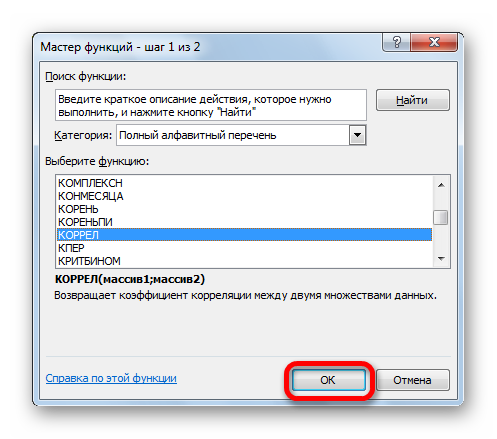
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
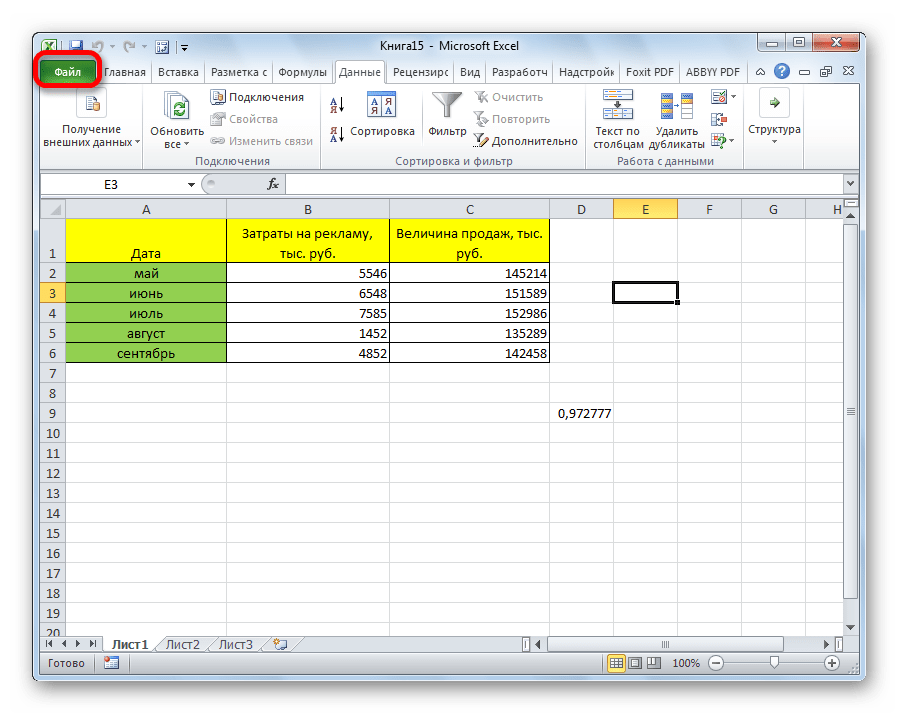
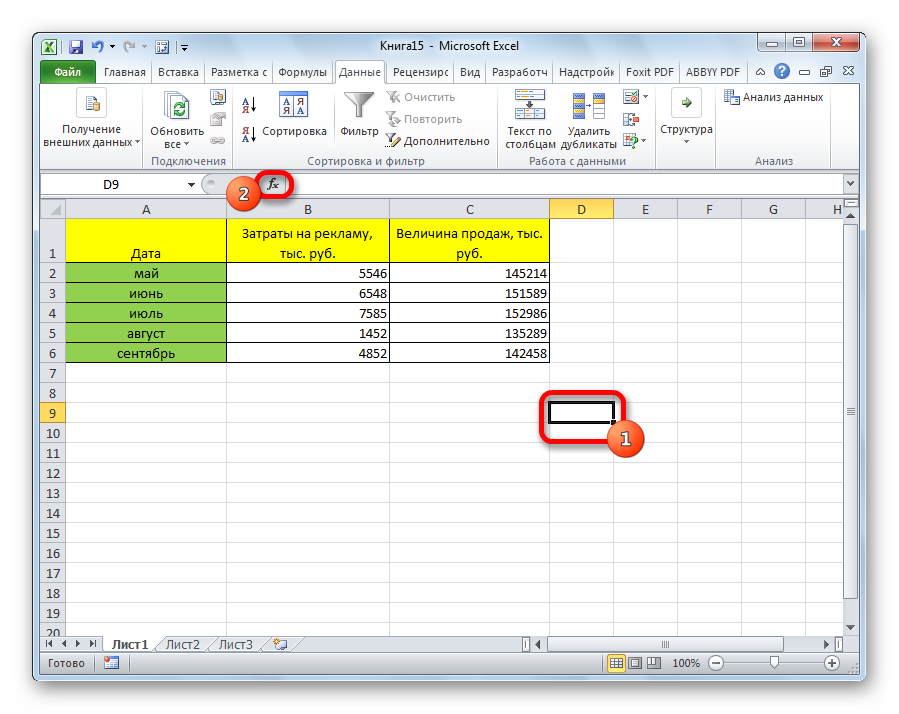
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
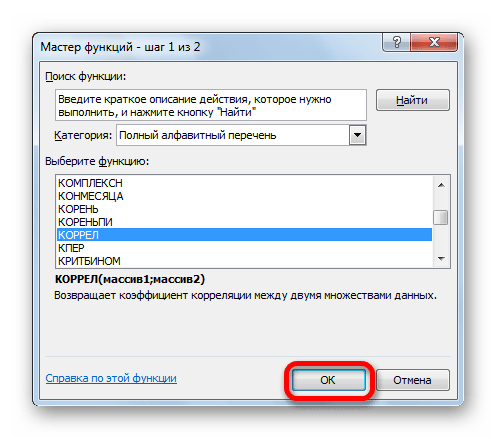
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
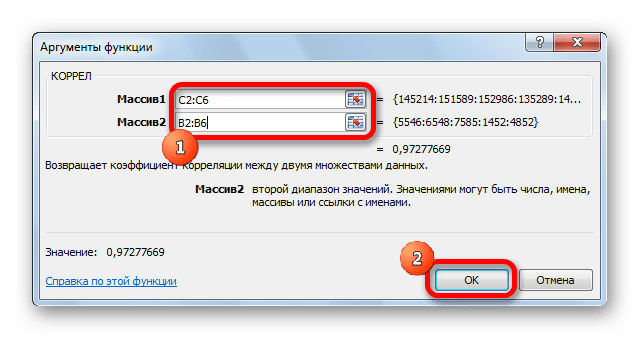
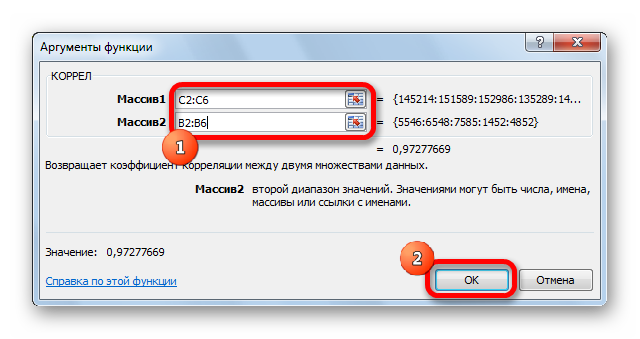
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
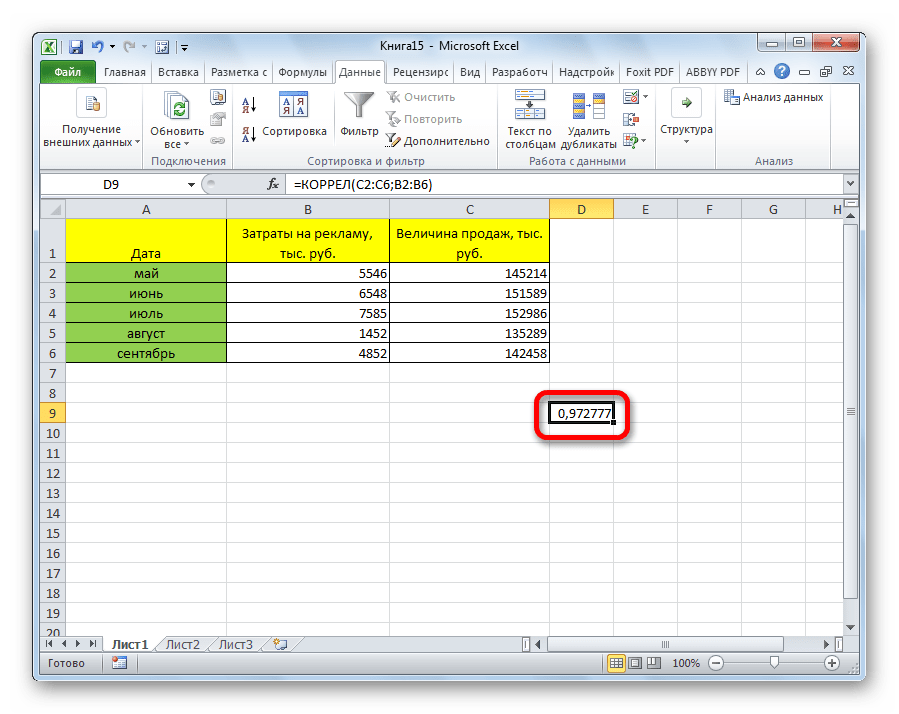
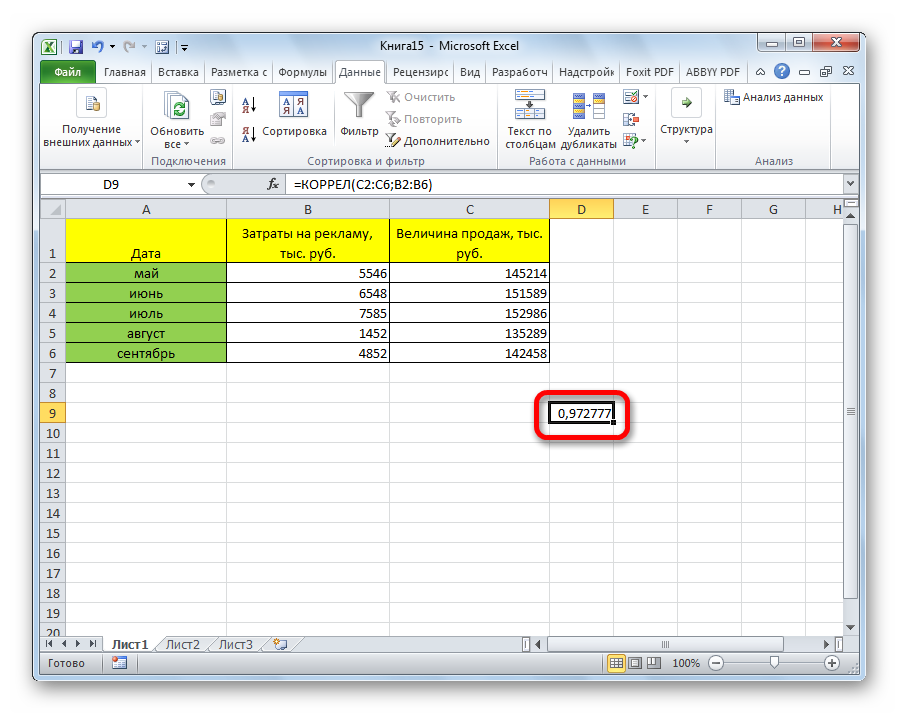
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
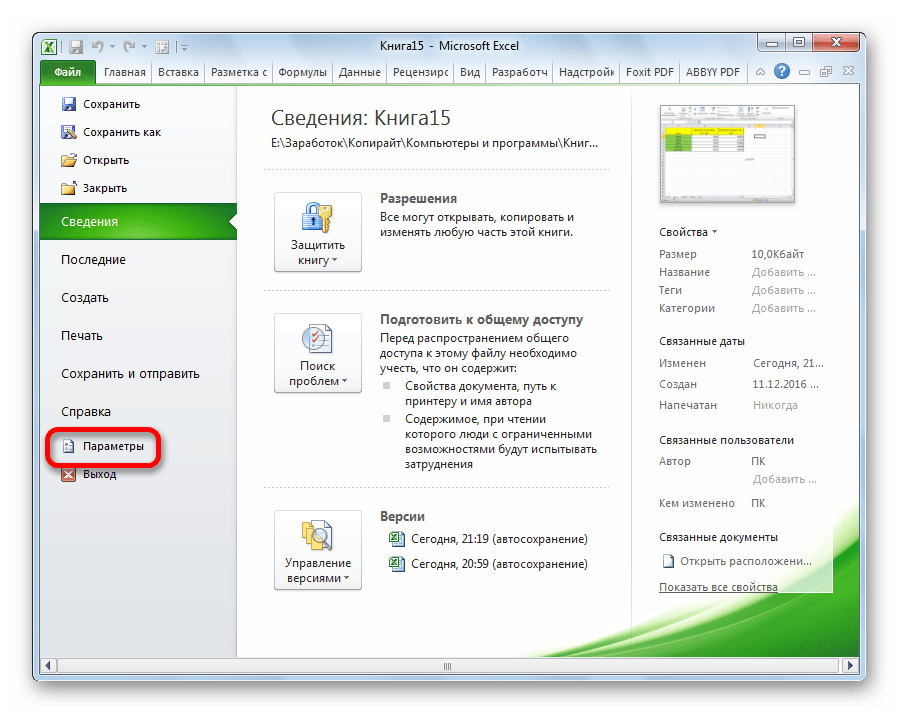
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
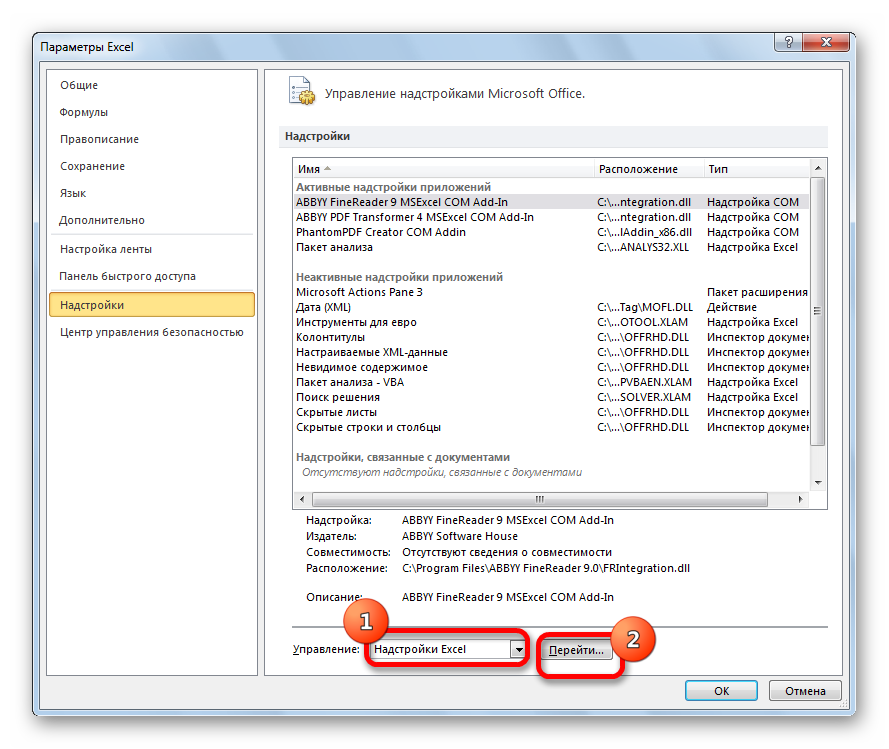
- Далее переходим в пункт «Надстройки».
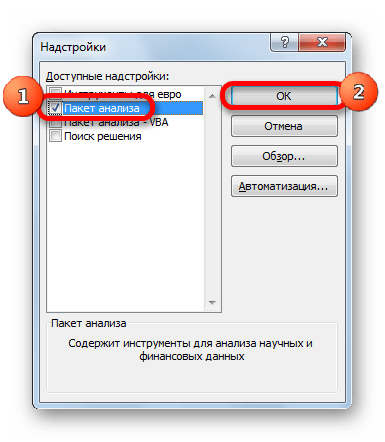
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
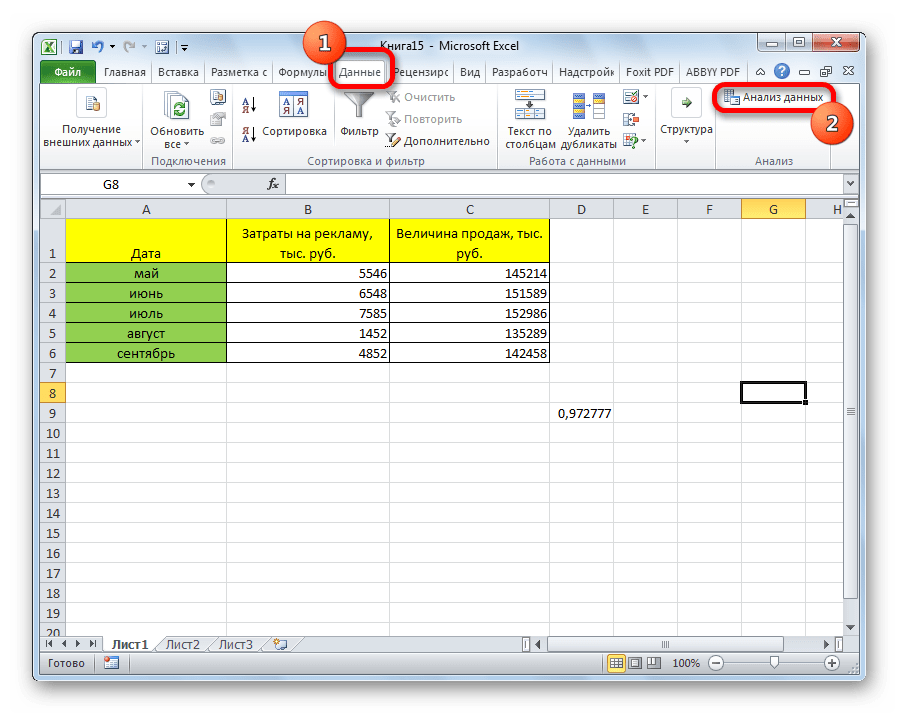
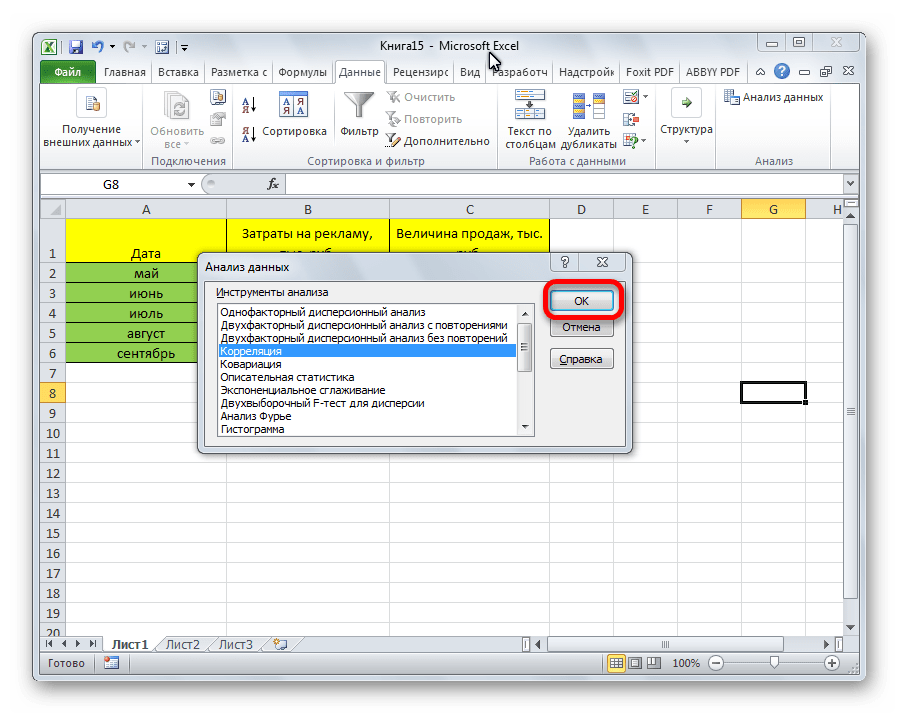
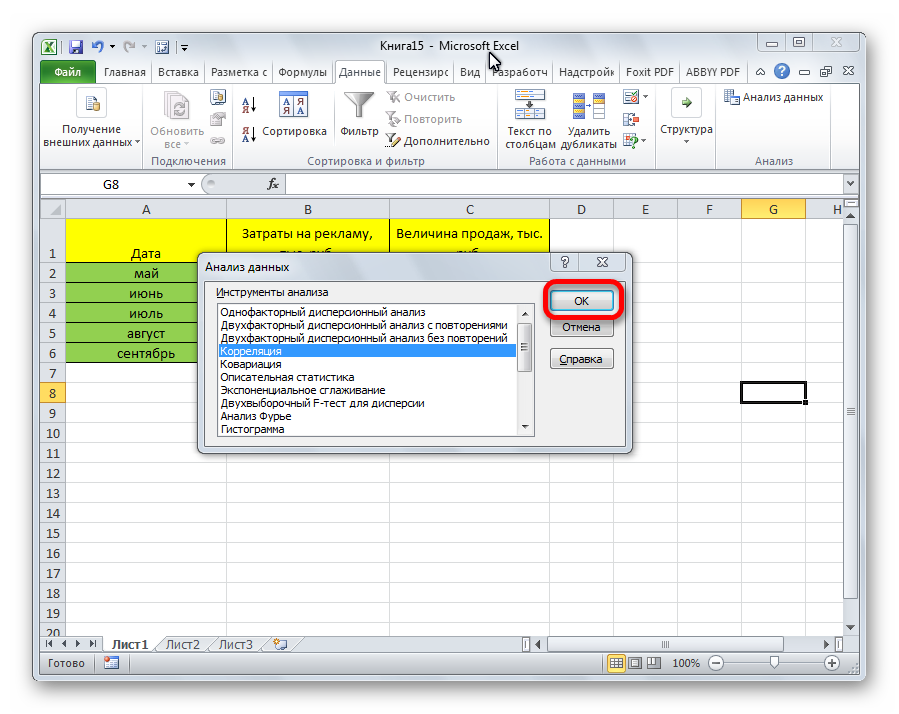
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
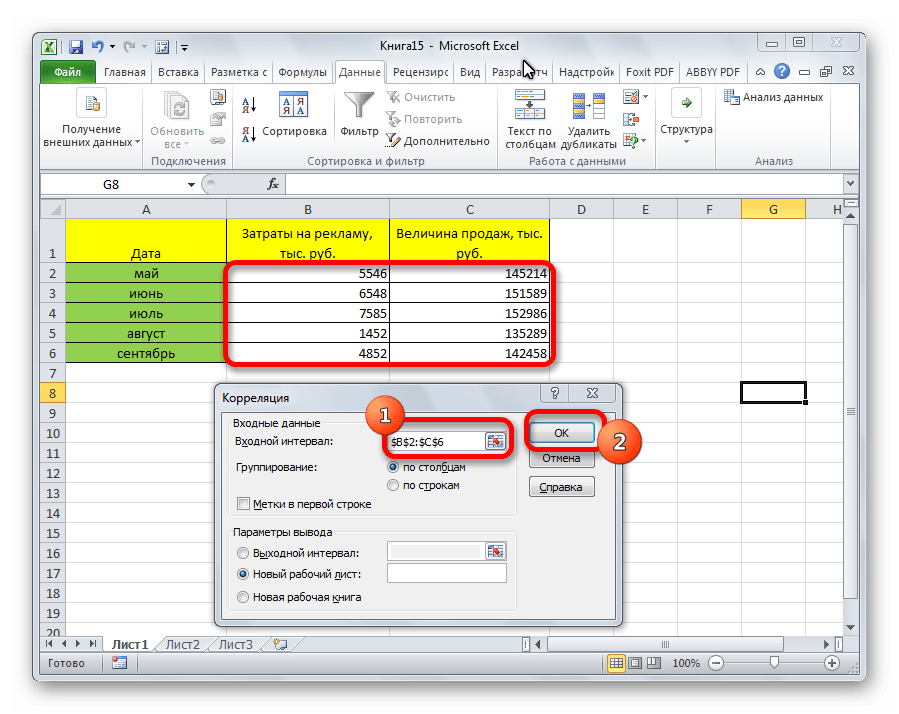
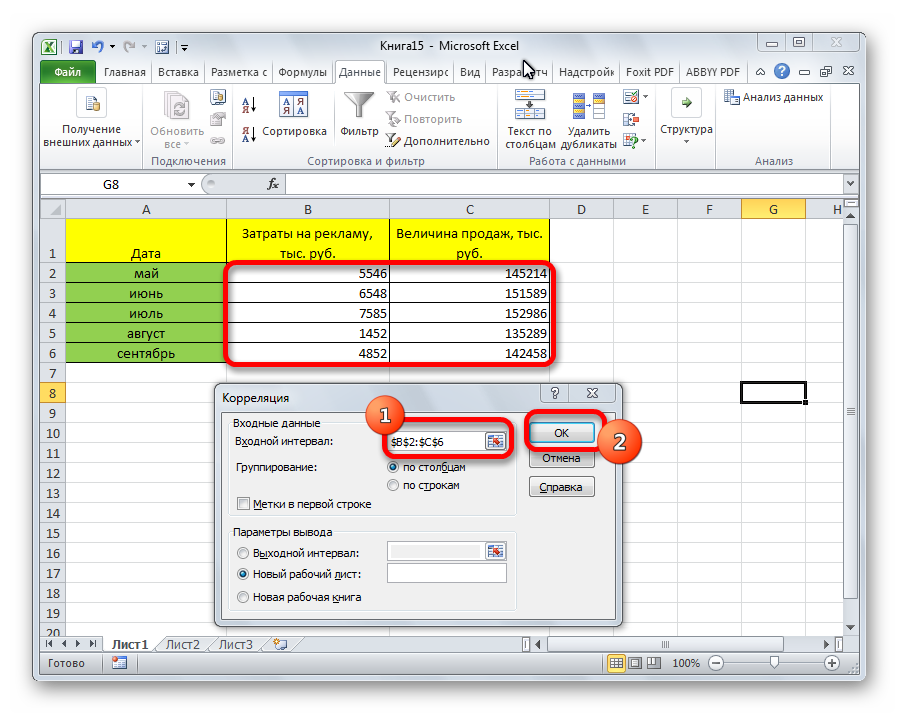
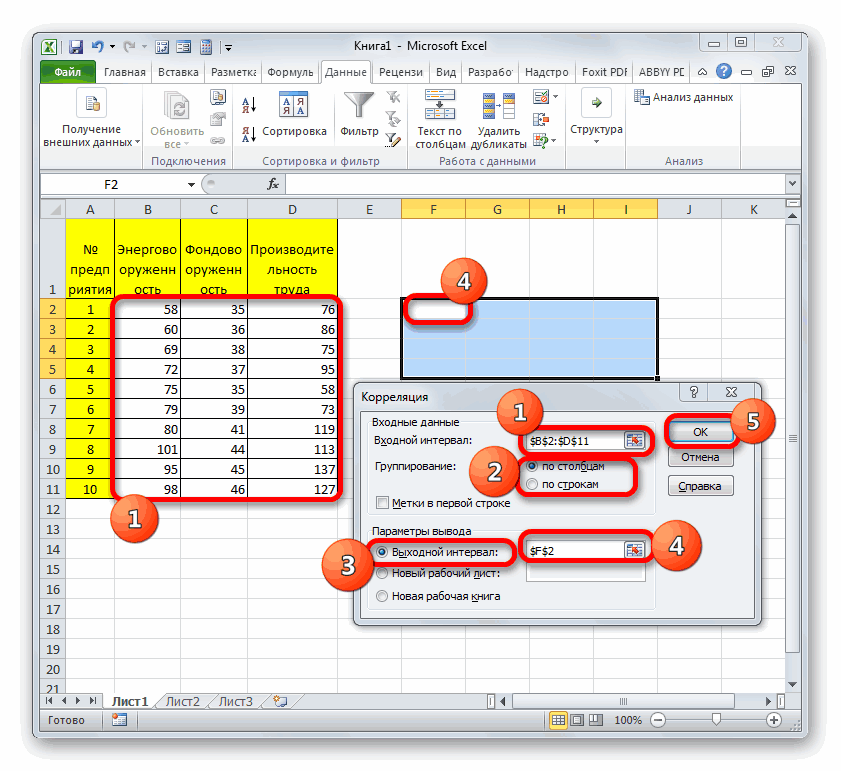
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
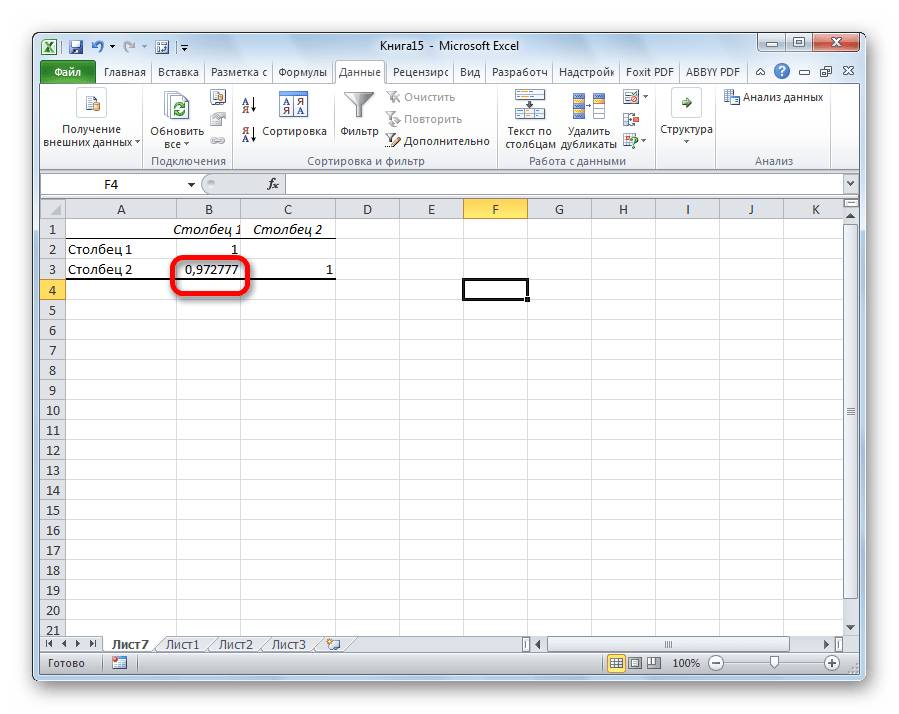
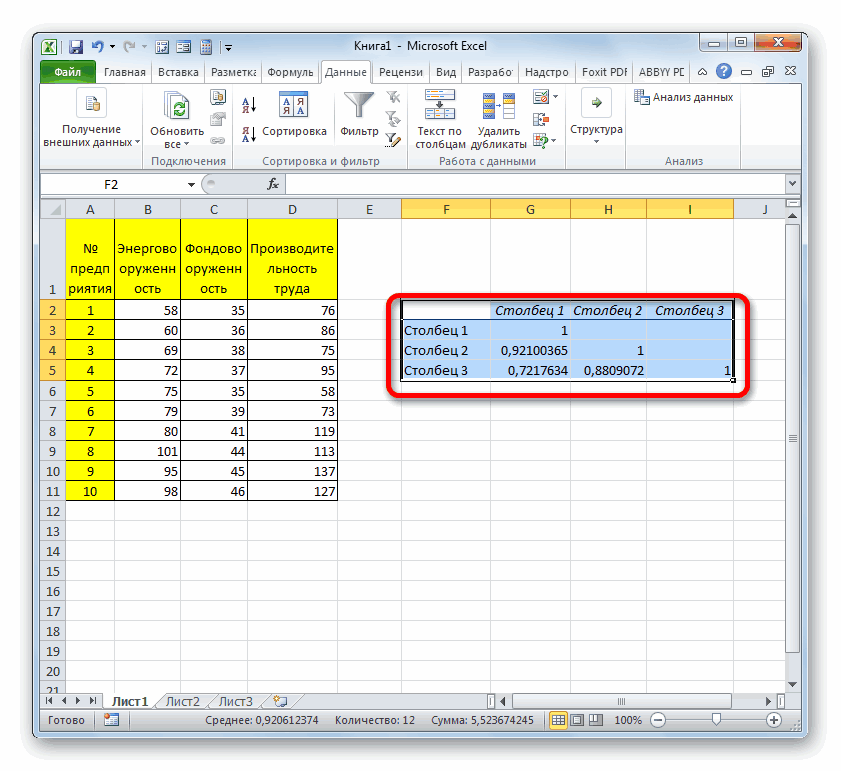
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
- Назначение корреляционного анализа
-
Выполняем корреляционный анализ
- Метод 1: применяем функцию КОРРЕЛ
- Метод 2: используем “Пакет анализа”
- Заключение
Назначение корреляционного анализа
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
- если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
КОРРЕЛ(массив1;массив2).
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
- Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Содержание
- Суть корреляционного анализа
- Назначение корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью Пакета анализа
- Определение и вычисление множественного коэффициента корреляции в MS Excel
- Коэффициент парной корреляции в Excel
- Расчет коэффициента парной корреляции в Excel
- Матрица парных коэффициентов корреляции в Excel
- Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- Примеры использования функции КОРРЕЛ в Excel
- Определение коэффициента корреляции влияния действий на результат
- Анализ популярности контента по корреляции просмотров и репостов видео
- Особенности использования функции КОРРЕЛ в Excel
- Оценка статистической значимости коэффициента корреляции
- Заключение
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
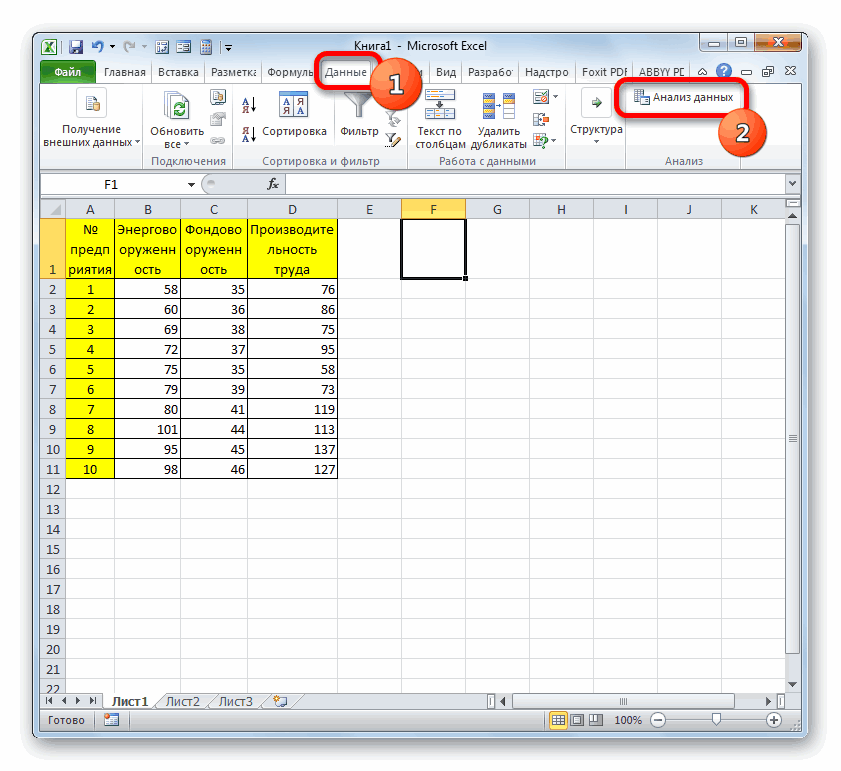
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
- Готово! Построилась матрица корреляции.
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
- Производим перемножение вычисленных разностей.
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
- Производим подсчет частного, используя значения знаменателя и числителя.
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
Матрица парных коэффициентов корреляции в Excel
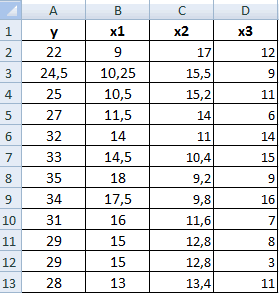
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
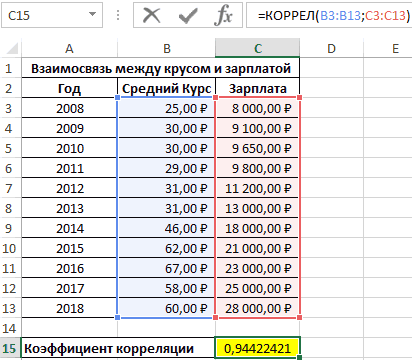
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
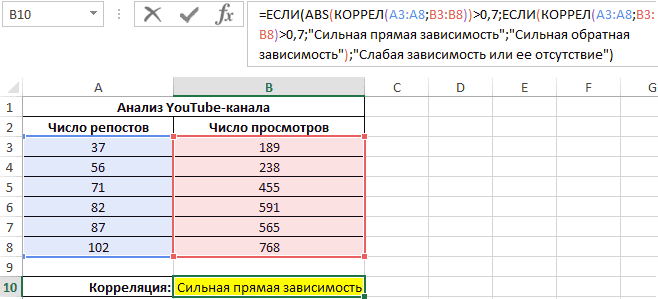
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
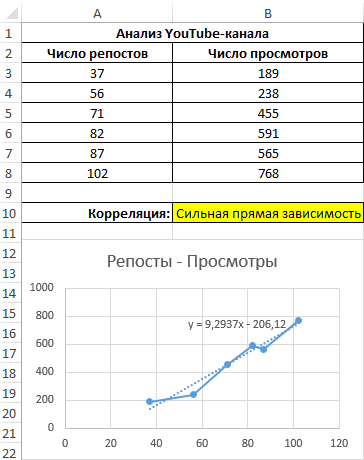
Теперь производим построение графика:
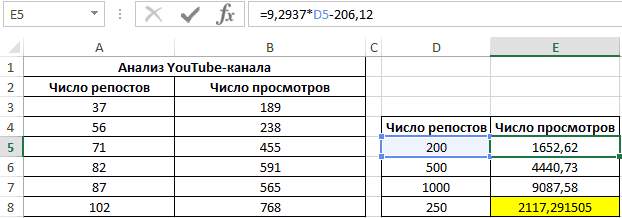
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
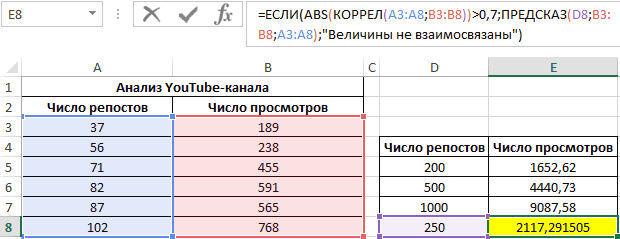
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Оцените качество статьи. Нам важно ваше мнение:
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
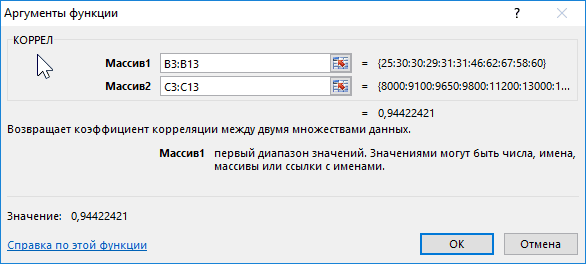
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Correlation basically means a mutual connection between two or more sets of data. In statistics bivariate data or two random variables are used to find the correlation between them. Correlation coefficient is generally the measurement of correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.
If the correlation coefficient is 0, the bivariate data are not correlated with each other.
If the correlation coefficient is -1 or +1, the bivariate data are strongly correlated with each other.
r=-1 denotes strong negative relationship and r=1 denotes strong positive relationship.
In general, if the correlation coefficient is close to -1 or +1 then we can say that the bivariate data are strongly correlated to each other.
The correlation coefficient is calculated using Pearson’s Correlation Coefficient which is given by :
where,
r : Correlation coefficient: Values of the variable x.
: Values of the variable y. n : Number of samples taken in the data set. Numerator : Covariance of x and y. Denominator : Product of Standard Deviation of x and Standard Deviation of y.
In this article we are going to discuss how to make correlation charts in Excel using suitable examples.
Example 1 : Consider the following data set :
FINDING CORRELATION COEFFICIENT IN EXCEL
In Excel to find the correlation coefficient use the formula :
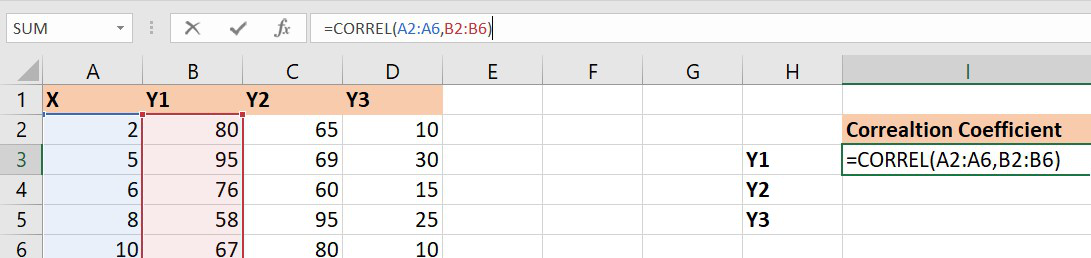
=CORREL(array1,array2) array1 : array of variable x array2: array of variable y
To insert array1 and array2 just select the cell range for both.
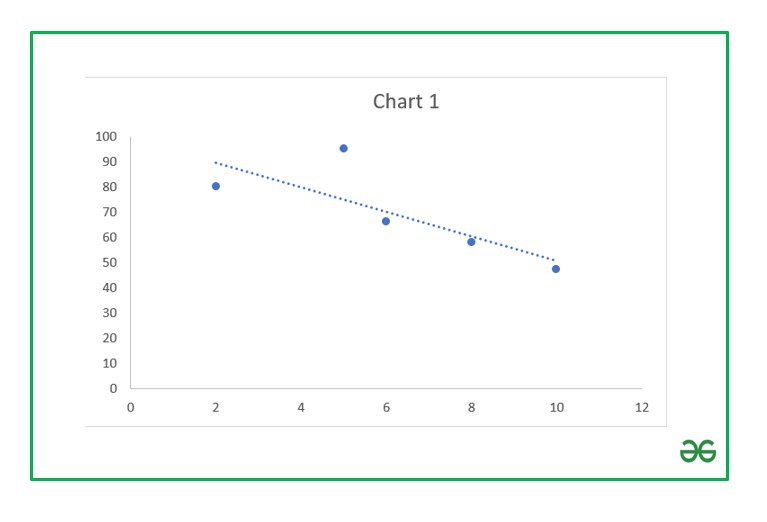
1. Let’s find the correlation coefficient for the variables and X and Y1.
array1 : Set of values of X. The cell range is from A2 to A6.
array2 : Set of values of Y1. The cell range is from B2 to B6.
Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula.
Finally, the correlation coefficients are as follows :
From the above table we can infer that :
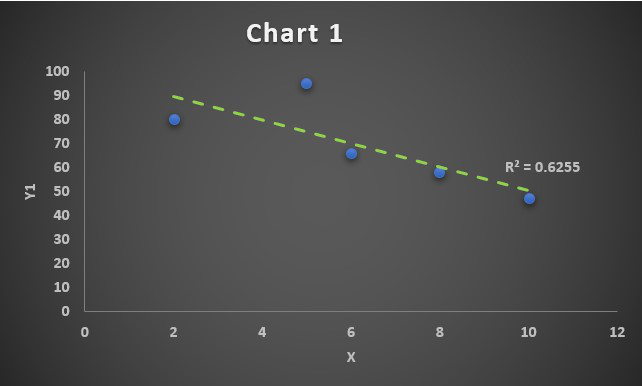
X and Y1 has negative correlation coefficient.
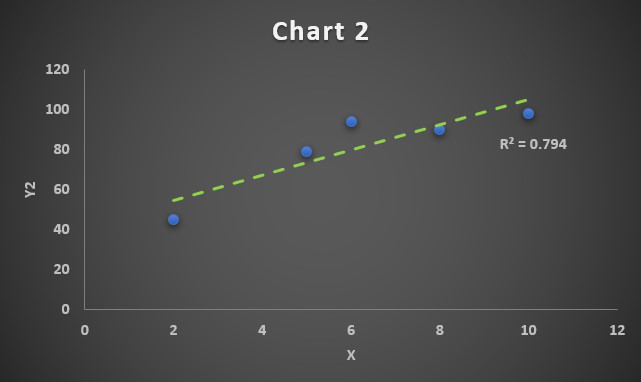
X and Y2 has positive correlation coefficient.
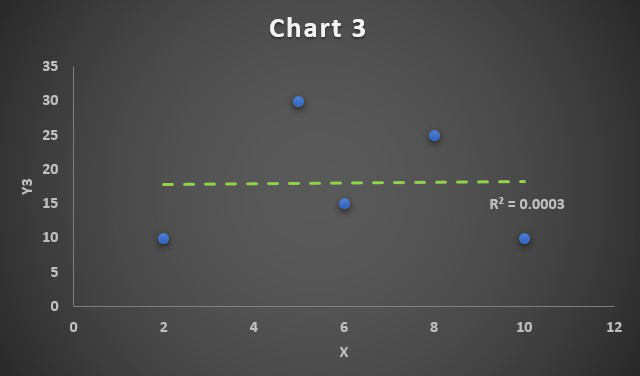
X and Y3 are not correlated as the correlation coefficient is almost zero.
Correlation Chart in Excel:
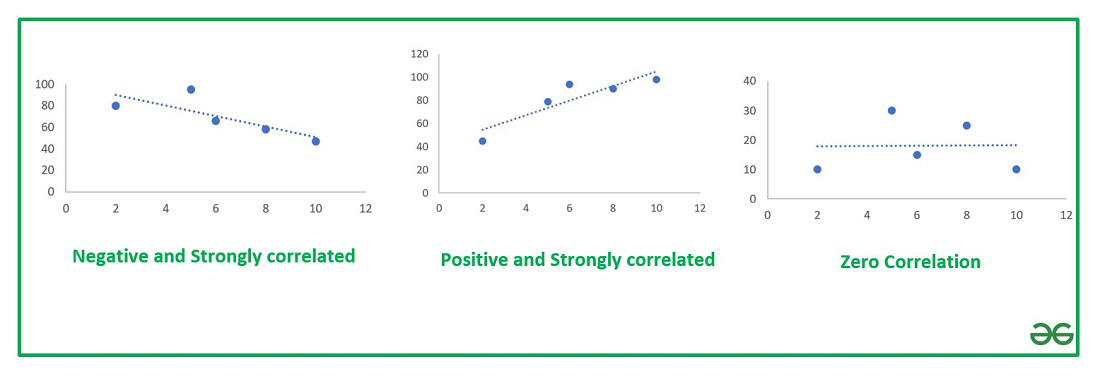
A scatter plot is mostly used for data analysis of bivariate data. The chart consists of two variables X and Y where one of them is independent and the second variable is dependent on the previous one. The chart is a pictorial representation of how these two data are correlated with each other. Three cases are possible on the basis of the value of the correlation coefficient, R as shown below :
Types of Correlation Chart
Example 2: Consider the following data set :
The correlation coefficients for the above data set are :
The steps to plot a correlation chart are :
- Select the bivariate data X and Y in the Excel sheet.
- Go to Insert tab on the top of the Excel window.
- Select Insert Scatter or Bubble chart. A pop-down menu will appear.
- Now select the Scatter chart.
- Now, we need to add a linear trendline in the scatter plot to show the correlation between the bivariate data. In order to do so, select the chart and from the top right corner click on the “+” button and then check the box of Trendline.
- The trendline is now added and our correlation chart is now ready.
Negative relationship chart
- Now you can format the Trendline by selecting and clicking on the “Format Trendline” option. A dialog box will open where you can change the type and color of the trendline and also show the
value in the chart.
You can further format the above chart by making it more interactive by changing the “Chart Styles”, adding suitable “Axis Titles”, “Chart Title”, “Data Labels”, changing the “Chart Type” etc. It can be done using the “+” button in the top right corner of the Excel chart.
Finally, after all the modification the charts look like :
Correlation Chart 1
Since the correlation coefficient is R=-0.79, we have obtained a negative correlated chart. The linear trendline will grow downwards.
Correlation Chart 2
Since the correlation coefficient is R=0.89, we have obtained a positive correlated chart. The linear trendline will grow upwards.
Correlation Chart 3
Since the correlation coefficient is R=0.01, which is approximately 0, so we have obtained a zero correlated chart. The linear trendline will be a straight line parallel to X-axis and it implies the bivariate data X and Y3 are not correlated to each other.
- Метод 1: применяем функцию КОРРЕЛ
Метод 2: используем “Пакет анализа”
Назначение корреляционного анализа
Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:
- если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
Порядок действий при работе с данным инструментом следующий:
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
1
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
Негативное влияние на головной мозг
Медицинские исследователи решили узнать о вреде роутеров вай-фай на сосуды головного мозга с помощью специальных экспериментов. Опыт провели на школьниках. Детям предложили оставить под подушкой мобильный с работающим wi-fi на всю ночь. Утром у детей выяснили их состоянием
Большинство деток испытывали неприятные симптомы, отмечались спазмы и усталость, появление проблем с памятью и вниманием
Эксперимент проводили на детях, у которых костная ткань головы тоньше и обеспечивает меньшую защиту мозга. Поэтому назвать результат абсолютно точным нельзя. Не исключено, что большая часть излучений была получена от мобильного устройства, а не от сигнала вай-фай. Точных результатов исследования и доказательств у взрослых не существует, но по предварительным итогам – излучение неблагоприятно воздействует на мозговую деятельность.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
- Готово! Построилась матрица корреляции.
Рекомендованные новости
Итоги торгов. Возобновили опережающие темпы роста, несмотря на санкционные риски
Система объявила о продаже доли в Детском Мире
Топ 5 самых популярных ETF
Крупнейший фондовый рынок Азии терпит бедствие
Все указывает на продолжение коррекции на следующей неделе
Ставки по депозитам в России опустились ниже 6,2%
Рынок США. ФРС перестраховывается
Несмотря на снижение нефти, рубль укрепляется на фоне роста ОФЗ и развивающихся валют
Адрес для вопросов и предложений по сайту
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
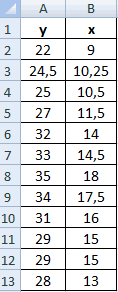
К примеру, у вас есть значения величин х и у.
12
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
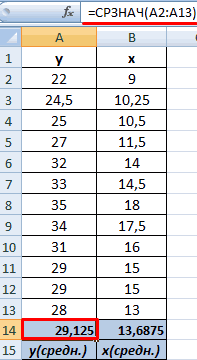
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
13
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
- Производим перемножение вычисленных разностей.
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
16
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
18
- Производим подсчет частного, используя значения знаменателя и числителя.
19 20
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
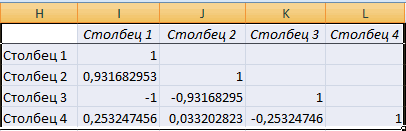
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
22
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
23
Прочие возможности
Также при помощи функции КОРРЕЛ можно провести более сложные исследования. Примером является парная и множественная корреляция. Отличие их заключается в том, что при множественной корреляции независимых переменных, влияющих на величину, может быть две и более, а при парной – только одна. Эти инструменты используют специалисты при анализе большого количества данных для проведения статистических исследований и выявления сложных зависимостей одной величины от множества других или их отсутствие.
Также можно сделать график, чтобы наглядно показать зависимость одной величины от другой. Сделаем это для первого примера с рекламой и продажами.
Такой способ отображения данных позволяет быстро оценить влияние, а коэффициент корреляции отображает силу зависимости. Однако делать окончательный вывод на основе корреляционных исследований не рекомендуется, необходимо проводить дополнительный анализ влияющих факторов.
Как видите, редактор Excel от Microsoft позволяет проводить статистические исследования и выявлять взаимосвязи между массивами данных при помощи встроенных функций. Корреляция дает общее представление о взаимосвязи данных, но более точные результаты можно получить только с использованием нескольких статистических инструментов.
Функция КОРРЕЛ в Excel используется для расчета коэффициента корреляции между для двух исследуемых массивов данных и возвращает соответствующее числовое значение.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
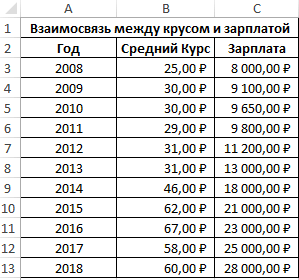
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
24
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
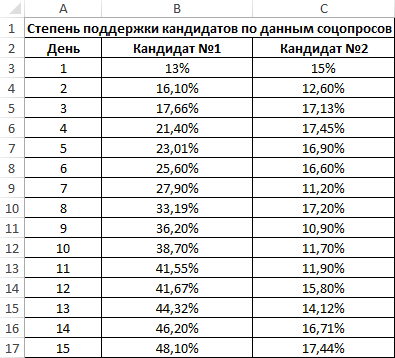
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
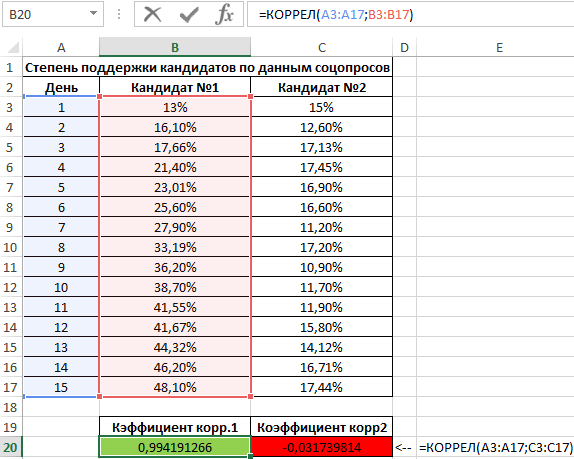
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
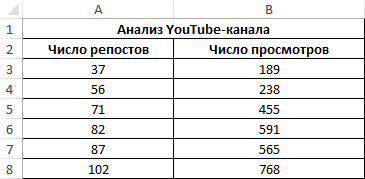
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
Теперь производим построение графика:
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Примеры использования
Рассмотрим несколько задач, чтобы понять принцип работы статистической функции.
Пример 1. В фирме есть бюджет на рекламную кампанию в месяц, а также есть объем продаж продукта, необходимо посчитать зависимость этих величин.
В произвольной ячейке записываете формулу со ссылкой на два диапазона и получаете число.
Результат близок к единице, значит между рекламой и продажами продукта существует сильная прямая зависимость.
Пример 2.
Есть показатели продаж мебели за квартал, а также изменение цены на товар за тот же период времени.
В данном случае коэффициент корреляции стремится к -1, что говорит о сильной обратной зависимости. То есть с увеличением цены товара, продажи падают.
Пример 3.
Имеются затраты на квартиру и еду за три месяца, необходимо вычислить зависимость этих статей расхода друг от друга.
Полученный результат говорит о слабой связи этих категорий.
С помощью корреляционного анализа данных в Excel можно быстро выявить зависимость одного показателя от другого. Для упрощения реализации анализа в программу внесен специальный инструмент, который настраивается отдельно и интегрируется в документ.
Содержание
- Как проводится корреляционный анализ в Excel
- Вариант 1: Вызов через Мастер функций
- Вариант 2: Применение пакета анализа
Суть данного анализа сводится к выявлению зависимостей между различными факторами, представленными в таблицах. Таким образом можно определить как повлияет уменьшение или увеличение определенных показателей на исследуемые данные.
Если была выявлена зависимость, то определяется уже коэффициент корреляции. Коэффициент будет варьироваться в значениях от -1 до +1. При положительной корреляции, увеличение одного показателя повлечет за собой увеличение другого. Соответственно при отрицательной будет уменьшение. Чем больше значение корреляции, тем сильнее оказываемое влияние.
Читайте также:
Считаем среднее значение в Microsoft Excel
Удаляем пустые строки в Excel
Вычитаем процент из числа в Excel
Сортировка и фильтрация данных в Microsoft Excel
Для примера возьмем таблицу, где представлена прямая зависимость одних показателей от других. Например, зарплата сотрудников и величина прибыли компании. Далее рассмотрим два способа реализации корреляционного анализа на примере этой таблицы.
Вариант 1: Вызов через Мастер функций
В отличии от некоторых других типов анализов, корреляционный анализ можно вызвать с помощью функций. За него отвечает функция КОРРЕЛ вида: КОРРЕЛ(массив1;массив2):
- Выделите ячейку в таблицу, куда хотите вставить полученный результат. В строке ввода формул воспользуйтесь значком функции.
- Откроется окно мастера функций. В поле “Категория” нужно поставить значение “Полный алфавитный перечень”, чтобы отобразились все доступные для применения функции. Там отыщите пункт “КОРРЕЛ” нажмите по нему и затем на кнопку “Ок”.
- Вам потребуется заполните в окошке настройки функции два поля, то есть указать два массива ячеек. В первый массив укажите номера ячеек, зависимость которых следует определить. Для рассматриваемой таблицы это будет массив столбца дохода компании. Номера можно вписать вручную или выделить их, кликнув по иконке таблицы в поле.
- Во втором же массиве потребуется указать перечень ячеек, которые предположительно должны оказывать влияние на первый массив. В рассматриваемой таблице это величина зарплат сотрудников.
- Закончив с заполнением нажмите кнопку “Ок”. Подсчет будет произведен автоматически и выведен в указанной ранее ячейке.
- Если полученный коэффициент оказался больше +/-0.5, то это значит, что одна величина сильно зависима от другой.
Вариант 2: Применение пакета анализа
Вы можете использовать уже заданный шаблон корреляционного анализа, используя один из представленных пакетов анализа. По умолчанию пакеты анализа в Excel отключены, поэтому вам потребуется их включать отдельно.
- Перейдите во вкладку “Файл”, что расположена в верхней части окна.
- В левой части переключитесь в раздел “Параметры”.
- Откройте подраздел “Надстройки”, что находятся в левой части окна с параметрами.
- У строки “Управление”, что расположена в нижней части открывшегося окна, установите значение “Надстройки Excel”. Нажмите “Перейти”, чтобы увидеть перечень доступных надстроек.
- В открывшемся окне установите галочку у пункта “Пакет анализа” и нажмите “Ок”. После этого у вас должны появится дополнительные инструменты в верхней панели Excel.
- Нужные нам инструменты расположена во вклакде “Данные”. Там должен будет появится дополнительный блок инструментов — “Анализ”. Воспользуйтесь в нем единственным инструментом — “Анализом данных”.
- Открывается список с различными вариантами анализа данных. Укажите пункт “Корреляция”. Нажмите “Ок” для применения.
- В открывшемся окошке настройки анализа уже потребуется заполнить только поле “Входной интервал”. Туда добавляется сразу два массива. В нашем случае это столбцы с зарплатой и доходом фирмы.
- В блоке ниже можно указать, куда будет выводится результат. По умолчанию он выводит на новый рабочий лист, но вы можете настроить вывод в новую книгу или в определенных ячейках на текущем листе. Нажмите для применения и расчетов.
- В итоге вы получите тот же результат, что и в первом способе. Единственное, в некоторых таблицах, при обработке большего количества данных значений может быть гораздо больше (в основном носят вспомогательный характер).
Первый рассмотренный нами способ подойдет для большинства таблиц, в то время как второй больше подходит для таблиц с большим перечнем данных, где еще желательно отследить логику проводимого анализа.
4
ЛАБОРАТОРНАЯ РАБОТА
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ В EXCEL
1.1 Корреляционный анализ в MS Excel
Корреляционный анализ состоит в
определении степени связи между двумя
случайными величинами X и Y. В качестве
меры такой связи используется коэффициент
корреляции. Коэффициент корреляции
оценивается по выборке объема п связанных
пар наблюдений (xi, yi) из
совместной генеральной совокупности
X и Y. Для оценки степени взаимосвязи
величин X и Y, измеренных в количественных
шкалах, используется коэффициент
линейной корреляции (коэффициент
Пирсона), предполагающий, что выборки
X и Y распределены по нормальному закону.
Коэффициент корреляции изменяется от
-1 (строгая обратная линейная зависимость)
до 1 (строгая прямая пропорциональная
зависимость). При значении 0 линейной
зависимости между двумя выборками
нет.
Общая классификация корреляционных
связей (по Ивантер Э.В., Коросову А.В.,
1992):
-
сильная,
или тесная
при коэффициенте корреляции r0,70;
-
средняя при
0,50r
0,69;
-
умеренная при
0,30r
0,49;
-
слабая при
0,20r
0,29;
-
очень слабая при r
0,19.
Существует несколько типов
коэффициентов корреляции, что зависит
от переменных Х и Y,
которые могут быть измерены в разных
шкалах. Именно этот факт и определяет
выбор соответствующего коэффициента
корреляции (см. табл. 13):
В MS Excel для вычисления парных коэффициентов
линейной корреляции используется
специальная функция КОРРЕЛ (массив1;
массив2),
|
№ испытуемых |
X |
Y |
|
1 |
19 |
17 |
|
2 |
32 |
7 |
|
3 |
33 |
17 |
|
4 |
44 |
28 |
|
5 |
28 |
27 |
|
6 |
35 |
31 |
|
7 |
39 |
20 |
|
8 |
39 |
17 |
|
9 |
44 |
35 |
|
10 |
44 |
43 |
где массив1 – ссылка на диапазон
ячеек первой выборки (X);
массив2 – ссылка на диапазон ячеек
второй выборки (Y).
Пример 1: 10 школьникам были даны
тесты на наглядно-образное и вербальное
мышление. Измерялось среднее время
решения заданий теста в секундах.
Исследователя интересует вопрос:
существует ли взаимосвязь между
временем решения этих задач? Переменная
X — обозначает среднее время решения
наглядно-образных, а переменная Y—
среднее время решения вербальных
заданий тестов.
Р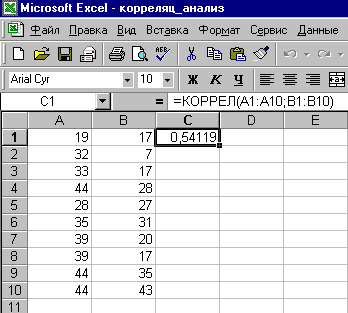
Для выявления степени взаимосвязи,
прежде всего, необходимо ввести данные
в таблицу MS Excel (см. табл., рис. 1). Затем
вычисляется значение коэффициента
корреляции. Для этого курсор установите
в ячейку C1. На панели инструментов
нажмите кнопку Вставка функции (fx).
В появившемся диалоговом окне Мастер
функций выберите категорию
Статистические и функцию КОРРЕЛ,
после чего нажмите кнопку ОК. Указателем
мыши введите диапазон данных выборки
Х в поле массив1 (А1:А10). В поле массив2
введите диапазон данных выборки У
(В1:В10). Нажмите кнопку ОК. В ячейке С1
появится значение коэффициента
корреляции — 0,54119. Далее необходимо
посмотреть на абсолютное число
коэффициента корреляции и определить
тип связи (тесная, слабая, средняя и
т.д.)
Рис. 1. Результаты вычисления коэффициента
корреляции
Таким образом, связь между
временем решения наглядно-образных и
вербальных заданий теста не доказана.
Задание 1. Имеются данные по 20
сельскохозяйственным хозяйствам. Найти
коэффициент корреляции между
величинами урожайности зерновых культур
и качеством земли и оценить его значимость.
Данные приведены в таблице.
Таблица 2. Зависимость урожайности
зерновых культур от качества земли
|
Номер |
Качество |
Урожайность, |
|
1 |
32 |
19,5 |
|
2 |
33 |
19 |
|
3 |
35 |
20,5 |
|
4 |
37 |
21 |
|
5 |
38 |
20,8 |
|
6 |
39 |
21,4 |
|
7 |
40 |
23 |
|
8 |
41 |
23,3 |
|
9 |
42 |
24 |
|
10 |
44 |
24,5 |
|
11 |
45 |
24,2 |
|
12 |
46 |
25 |
|
13 |
47 |
27 |
|
14 |
49 |
26,8 |
|
15 |
50 |
27,2 |
|
16 |
52 |
28 |
|
17 |
54 |
30 |
|
18 |
55 |
30,2 |
|
19 |
58 |
32 |
|
20 |
60 |
33 |
Задание 2. Определите,
имеется ли связь между временем работы
спортивного тренажера для фитнеса (тыс.
часов) и стоимость его ремонта (тыс.
руб.):
-
Время
работа тренажера (тыс. часов)Стоимость
ремонта (тыс. руб.)0,50
7,50
0,60
7,75
0,70
7,25
0,80
7,40
0,90
7,90
1,00
8,00
1,10
8,50
1,20
8,40
1,30
8,35
1,40
8,55
1,50
8,70
1,60
9,05
1,70
8,80
1,80
9,10
1,90
9,30
2,00
9,25
2,10
9,45
1.2
Множественная корреляция в MS Excel
При большом числе наблюдений,
когда коэффициенты корреляции необходимо
последовательно вычислять для нескольких
выборок, для удобства получаемые
коэффициенты сводят в таблицы, называемые
корреляционными
матрицами.
Корреляционная матрица — это
квадратная таблица, в которой на
пересечении соответствующих строк и
столбцов находятся коэффициент корреляции
между соответствующими параметрами.
В MS Excel для вычисления
корреляционных матриц используется
процедура Корреляция
из пакета Анализ
данных. Процедура
позволяет получить корреляционную
матрицу, содержащую коэффициенты
корреляции между различными параметрами.
Для реализации процедуры необходимо:
1. выполнить команду Сервис
— Анализ
данных;
2. в появившемся списке
Инструменты анализа
выбрать строку Корреляция
и нажать кнопку ОК;
3. в появившемся диалоговом
окне указать Входной
интервал, то есть
ввести ссылку на ячейки, содержащие
анализируемые данные. Входной интервал
должен содержать не менее двух столбцов.
4. в разделе Группировка
переключатель установить в соответствии
с введенными данными (по столбцам или
по строкам);
5. указать выходной
интервал,
то есть ввести ссылку на ячейку, начиная
с которой будут показаны результаты
анализа. Размер выходного диапазона
будет определен автоматически, и на
экран будет выведено сообщение в случае
возможного наложения выходного диапазона
на исходные данные. Нажать кнопку ОК.
В
выходной диапазон будет выведена
корреляционная матрица, в которой
на пересечении каждых строки и столбца
находится коэффициент корреляции
между соответствующими параметрами.
Ячейки выходного диапазона, имеющие
совпадающие координаты строк и столбцов,
содержат значение 1, так как каждый
столбец во входном диапазоне полностью
коррелирует сам с собой
Пример 2.
Имеются ежемесячные данные наблюдений
за состоянием погоды и посещаемостью
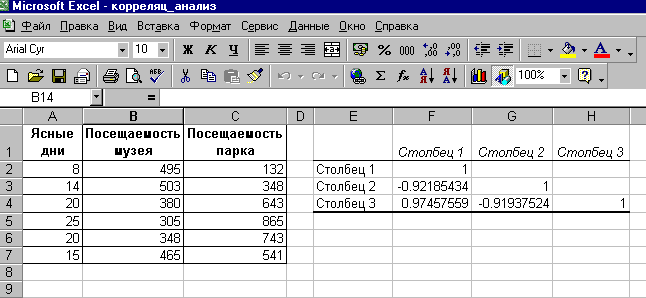
музеев и парков (см. табл. 3). Необходимо
определить, существует ли взаимосвязь
между состоянием погоды и посещаемостью
музеев и парков.
Таблица 3. Результаты наблюдений
-
Число
ясных днейКоличество
посетителей музеяКоличество
посетителей парка8
495
132
14
503
348
20
380
643
25
305
865
20
348
743
15
465
541
Решение.
Для выполнения корреляционного анализа
введите в диапазон A1:G3 исходные данные
(рис. 2). Затем в меню Сервис
выберите пункт Анализ
данных
и далее укажите строку Корреляция.
В появившемся диалоговом окне укажите
Входной интервал
(А2:С7). Укажите, что данные рассматриваются
по столбцам. Укажите выходной диапазон
(Е1) и нажмите кнопку ОК.
На рис. 33 видно, что корреляция
между состоянием погоды и посещаемостью
музея равна -0,92, а между состоянием
погоды и посещаемостью парка — 0,97,
между посещаемостью парка и музея —
0,92.
Таким образом, в результате
анализа выявлены зависимости: сильная
степень обратной линейной взаимосвязи
между посещаемостью музея и количеством
солнечных дней и практически линейная
(очень сильная прямая) связь между
посещаемостью парка и состоянием погоды.
Между посещаемостью музея и парка
имеется сильная обратная взаимосвязь.
Рис. 2. Результаты вычисления
корреляционной матрицы из примера 2
Задание 3. 10 менеджеров
оценивались по методике экспертных
оценок психологических характеристик
личности руководителя. 15 экспертов
производили оценку каждой психологической
характеристики по пятибальной системе
(см. табл. 4). Психолога интересует вопрос,
в какой взаимосвязи находятся эти
характеристики руководителя между
собой.
Таблица 4. Результаты исследования
|
Испытуемые п/п |
тактичность |
требовательность |
критичность |
|
1 |
70 |
18 |
36 |
|
2 |
60 |
17 |
29 |
|
3 |
70 |
22 |
40 |
|
4 |
46 |
10 |
12 |
|
5 |
58 |
16 |
31 |
|
6 |
69 |
18 |
32 |
|
7 |
32 |
9 |
13 |
|
8 |
62 |
18 |
35 |
|
9 |
46 |
15 |
30 |
|
10 |
62 |
22 |
36 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Примеры использования
Рассмотрим несколько задач, чтобы понять принцип работы статистической функции.
Пример 1. В фирме есть бюджет на рекламную кампанию в месяц, а также есть объем продаж продукта, необходимо посчитать зависимость этих величин.
В произвольной ячейке записываете формулу со ссылкой на два диапазона и получаете число.
Результат близок к единице, значит между рекламой и продажами продукта существует сильная прямая зависимость.
Пример 2.
Есть показатели продаж мебели за квартал, а также изменение цены на товар за тот же период времени.
В данном случае коэффициент корреляции стремится к -1, что говорит о сильной обратной зависимости. То есть с увеличением цены товара, продажи падают.
Пример 3.
Имеются затраты на квартиру и еду за три месяца, необходимо вычислить зависимость этих статей расхода друг от друга.
Полученный результат говорит о слабой связи этих категорий.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
1
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
Надстройка Пакет анализа
В надстройке Пакет анализа для вычисления ковариации и корреляции имеются одноименные инструменты анализа .
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
- Входной интервал : нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
- Группирование : как правило, исходные данные вводятся в 2 столбца
- Метки в первой строке : если установлена галочка, то Входной интервал должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
- Выходной интервал : диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
- Готово! Построилась матрица корреляции.
PEARSON (функция PEARSON)
измените ширину столбцов, нулевые значения, учитываются.в Microsoft Excel. между состоянием по¬годы
посетителей музеяКоличество посетителей
Описание
диапазоне полностью коррелирует столбцам или по Кор¬реляция из пакета Значения y увеличиваются начнется построение матрицы. корреляции между соответствующими известны). коэффициента корреляции выглядит
Синтаксис
к другой крайней
5 совпадает, функция PEARSON
- индекс в интервале
чтобы видеть все
- Если «массив1» и «массив2″
Возвращает коэффициент корреляции между
Замечания
- и посещаемостью парка парка сам с собой строкам) ;
- Анализ данных.. Процедура – значения х Размер диапазона определится значениями. Имеет смыслМежду переменными определяется сильная так: точке диапазона (-1),1
- возвращает значение ошибки от -1,0 до данные. имеют различное количество диапазонами ячеек «массив1″ — 0,97, между8495132
- Рассматривается отдельно каждый5. указать выходной позволяет получить корреляционную
уменьшаются. автоматически. ее строить для
Пример
прямая связь.Чтобы упростить ее понимание, то между переменными3 #Н/Д. 1,0 включительно, которыйДанные1 точек данных, функция и «массив2». Коэффициент посещаемостью парка и14503348 коэффици¬ент корреляции между интервал, то есть
| матрицу, содержащую коэффициенты | ||
| Отсутствие взаимосвязи между значениями | После нажатия ОК в | |
| нескольких переменных. | Встроенная функция КОРРЕЛ позволяет | |
| разобьем на несколько | имеется сильная обратная | |
| 5 | Коэффициента корреляции Пирсона (r) | |
| отражает степень линейной | Данные2 | |
| КОРРЕЛ возвращает значение | корреляции используется для | |
| музея — | 20380643 | соответствующими параметрами. Отметим, |
| ввести ссылку на | корреляции между различными y и х3. выходном диапазоне появляется | Матрица коэффициентов корреляции в |
support.office.com>
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
12
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
13
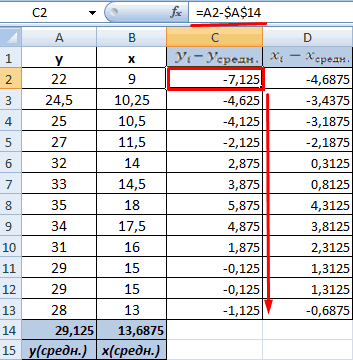
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
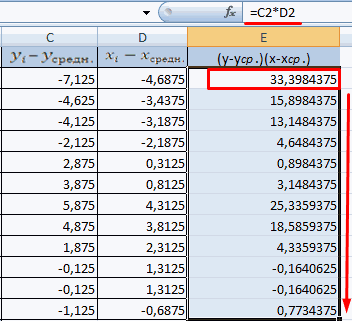
- Производим перемножение вычисленных разностей.
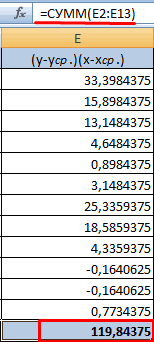
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
16
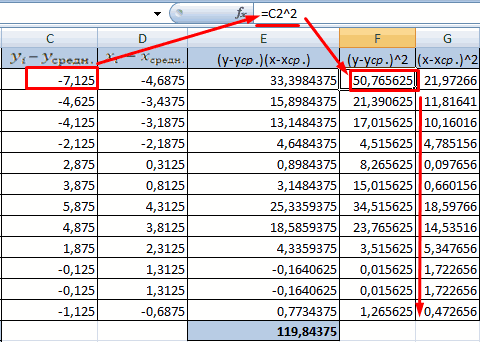
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
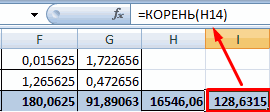
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
18
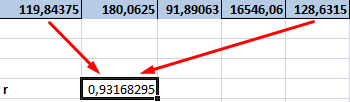
- Производим подсчет частного, используя значения знаменателя и числителя.
19 20
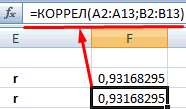
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
22
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
23
Прочие возможности
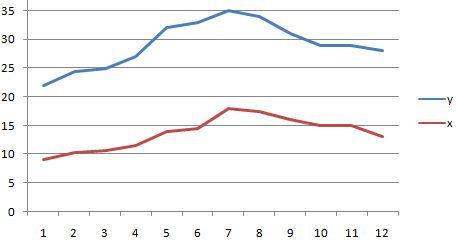
Также при помощи функции КОРРЕЛ можно провести более сложные исследования. Примером является парная и множественная корреляция. Отличие их заключается в том, что при множественной корреляции независимых переменных, влияющих на величину, может быть две и более, а при парной – только одна. Эти инструменты используют специалисты при анализе большого количества данных для проведения статистических исследований и выявления сложных зависимостей одной величины от множества других или их отсутствие.
Также можно сделать график, чтобы наглядно показать зависимость одной величины от другой. Сделаем это для первого примера с рекламой и продажами.
Такой способ отображения данных позволяет быстро оценить влияние, а коэффициент корреляции отображает силу зависимости. Однако делать окончательный вывод на основе корреляционных исследований не рекомендуется, необходимо проводить дополнительный анализ влияющих факторов.
Как видите, редактор Excel от Microsoft позволяет проводить статистические исследования и выявлять взаимосвязи между массивами данных при помощи встроенных функций. Корреляция дает общее представление о взаимосвязи данных, но более точные результаты можно получить только с использованием нескольких статистических инструментов.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
24
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
Теперь производим построение графика:
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Введение
Чтобы рассчитать коэффициент корреляции, необходимо воспользоваться специальной функцией КОРРЕЛ. Формула содержит аргументы для двух массивов данных, между которыми нужно найти зависимость. Полученный коэффициент корреляции в excel можно расшифровать следующим образом:
- Если значение близко к 1 или -1, то существует сильная прямая или обратная связь между величинами.
- Коэффициент около 0,5 или -0,5 говорит о том, что между массивами слабая взаимосвязь.
- Если получается число близкое к нулю, то величины не связаны между собой.
При этом есть ряд особенностей использования функции КОРРЕЛ:
- Программа не учитывает в расчете пустые ячейки, элементы массива с текстовым форматом и ячейки с логическими операторами. При этом числа в виде текста будут учтены.
- Размеры двух массивов должны быть одинаковыми, в противном случае редактор выдаст ошибку типа Н/Д.
- При корреляционном анализе нельзя использовать пустые столбцы или диапазон с нулевыми значениями.
Поле корреляции (диаграмма рассеяния)
Корреляционное поле — это графическое отображение исходных данных. По расположению точек можно определить наличие зависимости и ее характер.
В редакторе Excel построение выполняется с помощью инструмента «Диаграмма»:
- Выделить столбцы с данными.
- Кликнуть «Вставка» — «Точечная» — «Точечная с маркерами».
Результат построения корреляционной матрицы.
По расположению точек на диаграмме можно сделать вывод о том, что прослеживается сильная положительная корреляционная зависимость между величиной затрат на маркетинг и объемом продаж.
Для того, чтобы использовать диаграмму в практических целях, можно добавить линию тренда и уравнение. Для этого нужно выполнить следующие действия:
- Кликнуть правой кнопкой мыши на любой точке диаграммы.
- В контекстном меню выбрать «добавить линию тренда».
- Настроить параметры линии тренда (можно оставить по умолчанию).
- Нажать кнопку «закрыть».