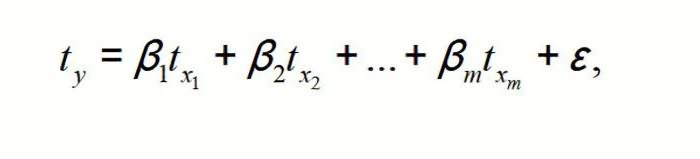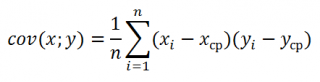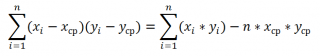Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
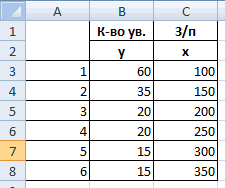
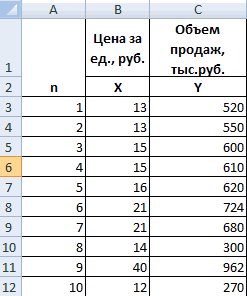
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
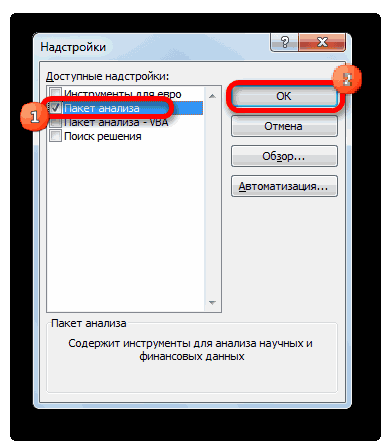
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
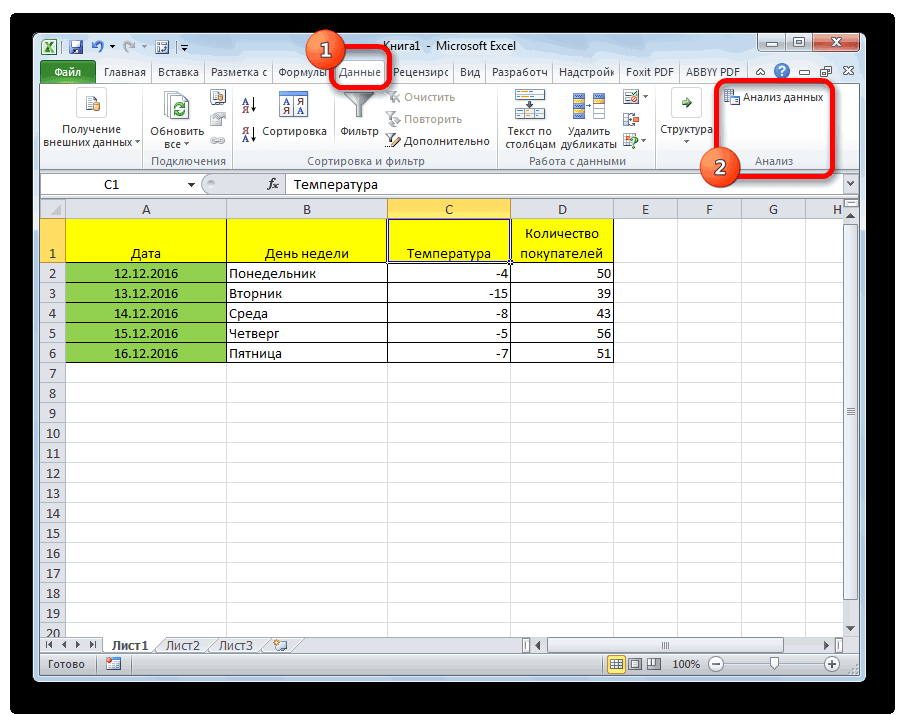
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
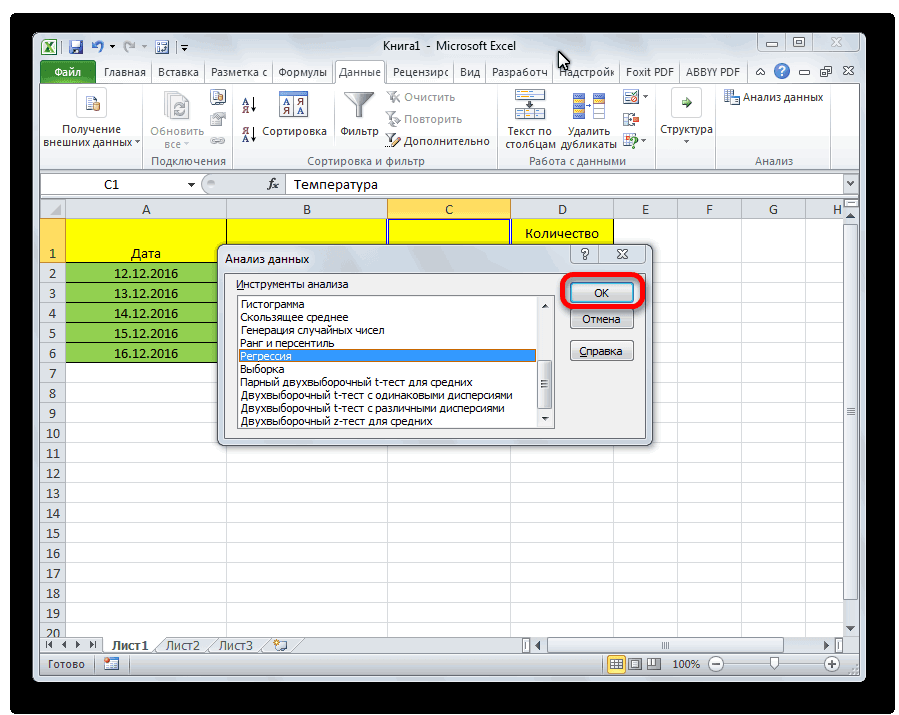
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
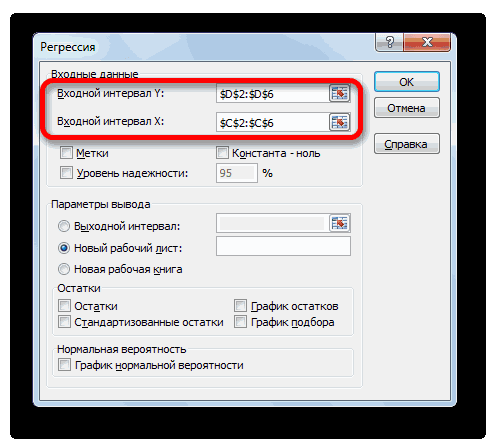
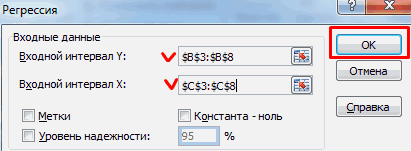
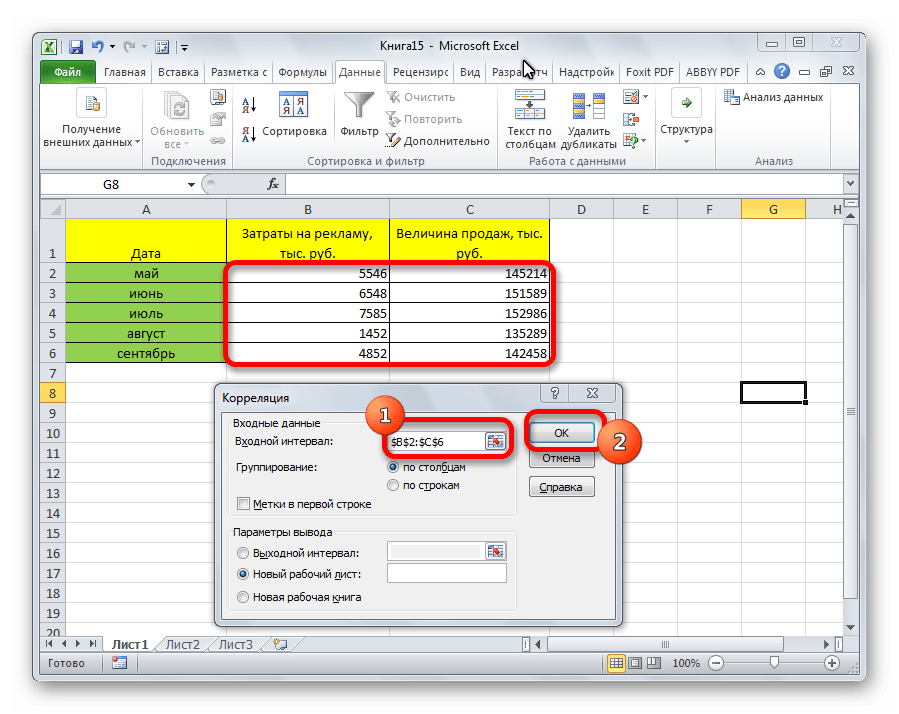
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
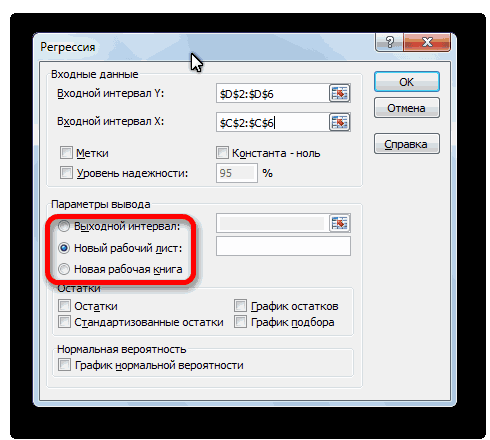
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
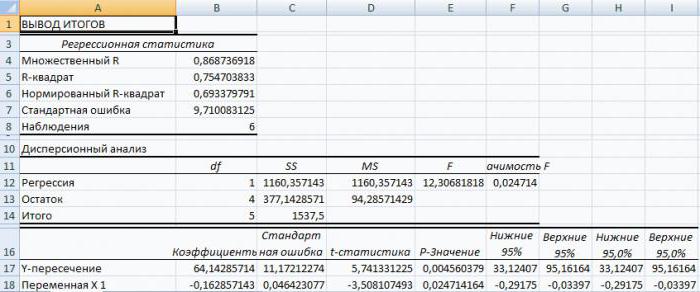
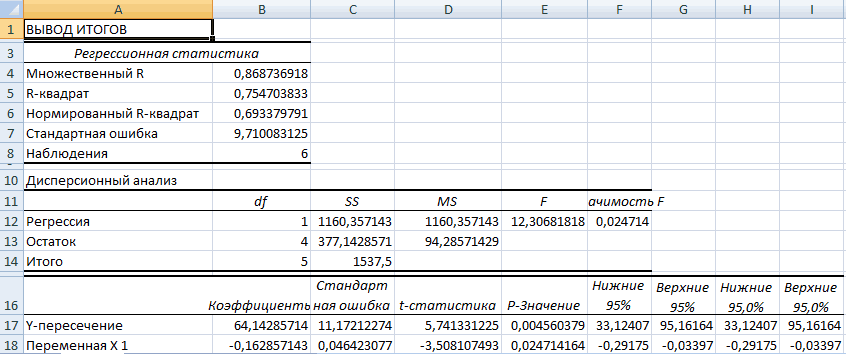
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
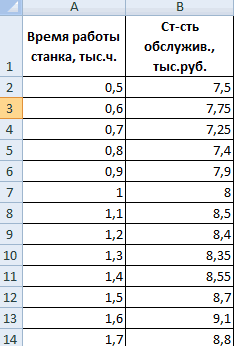
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
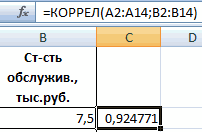
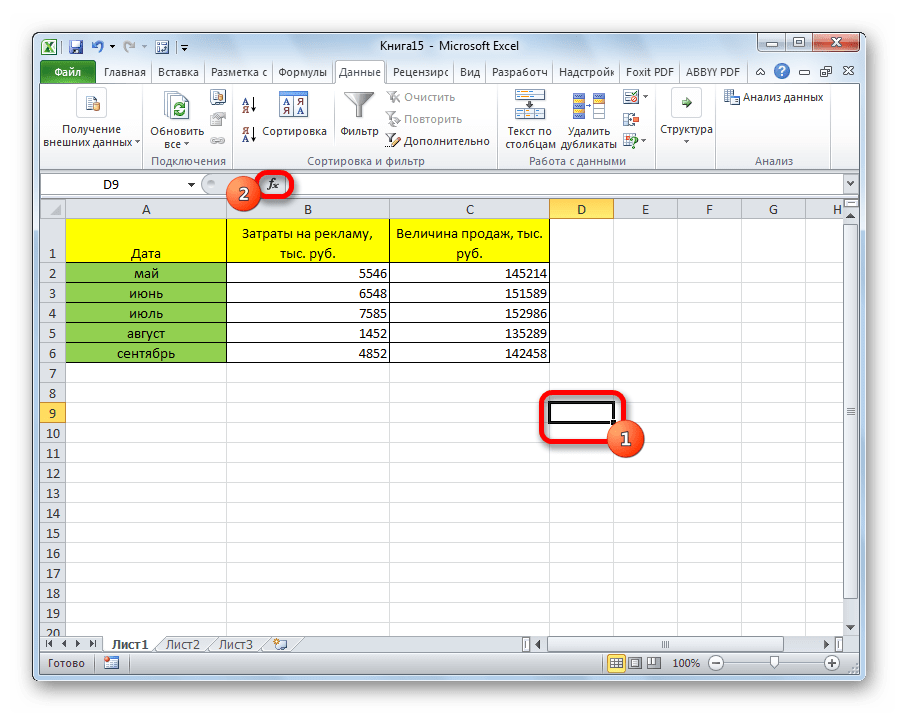
Ставим курсор в любую ячейку и нажимаем кнопку fx.
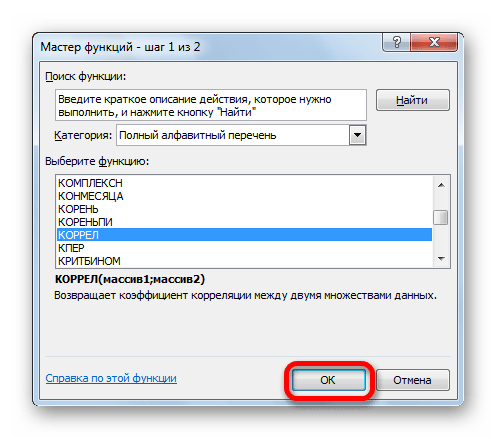
- В категории «Статистические» выбираем функцию КОРРЕЛ.
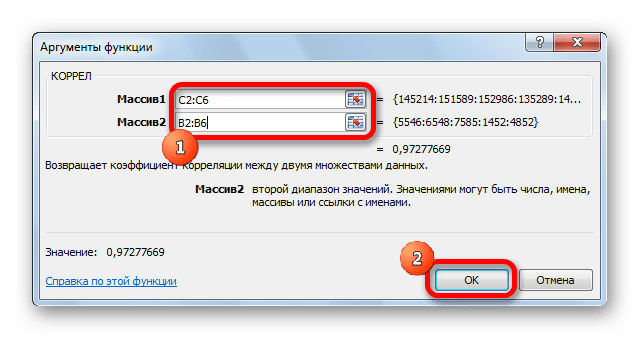
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
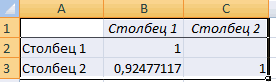
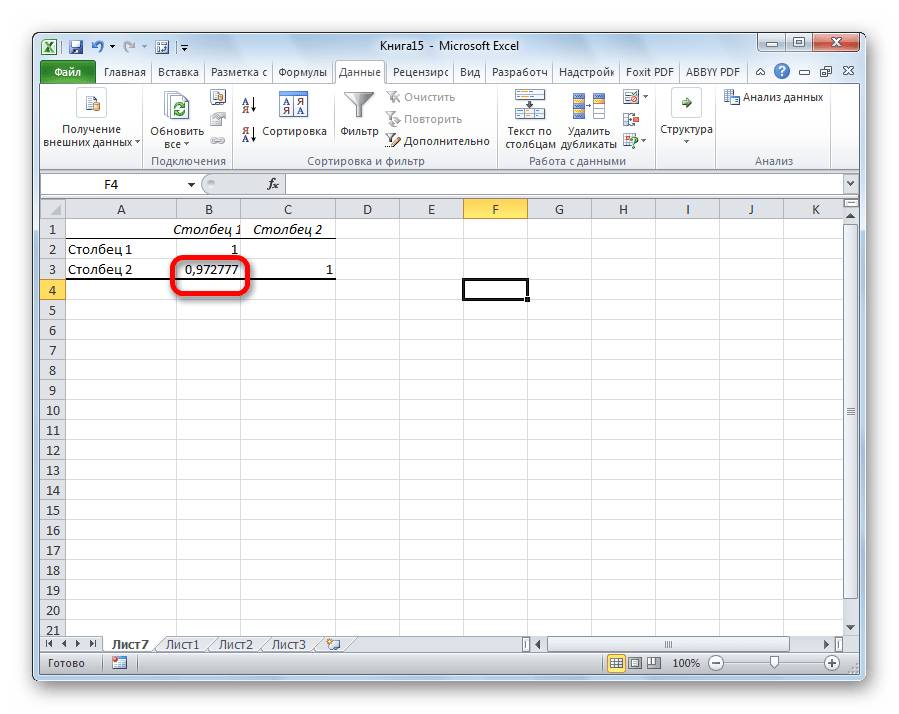
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
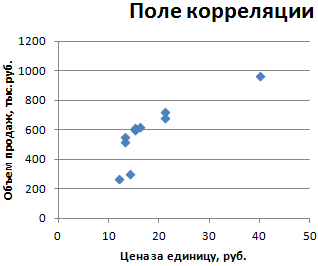
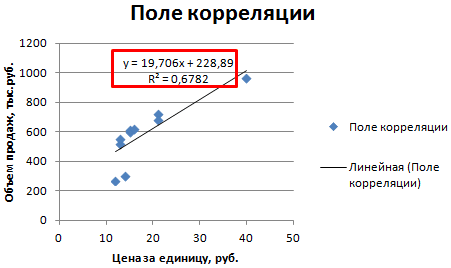
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
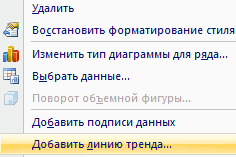
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
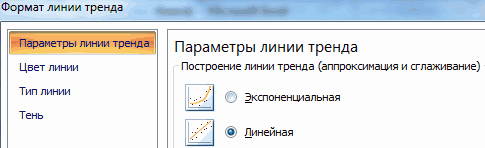
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Тема: КОРРЕЛЯЦИОННЫЙ
И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
ЛАБОРАТОРНАЯ
РАБОТА №1
1. ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИ В
ПРОГРАММЕ EXCEL
Корреляционная
связь — это
неполная, вероятностная зависимость
между показателями, которая проявляется
только в массе наблюдений.
Парная корреляция
— это связь
между двумя показателями, один из которых
является факторным, а другой —
результативным.
Множественная
корреляция возникает
от взаимодействия нескольких факторов
с результативным показателем.
Необходимые
условия применения корреляционного
анализа:
1. Наличие достаточно
большого количества наблюдений о
величине исследуемых факторных и
результативных показателей.
2. Исследуемые
факторы должны иметь количественное
измерение и отражение в тех или иных
источниках информации.
Применение
корреляционного анализа позволяет
решить следующие задачи:
1.Определить
изменение результативного показателя
под воздействием одного или нескольких
факторов.
2. Установить
относительную степень зависимости
результативного показателя от каждого
фактора.
Задание 1.
Имеются данные по
20 сельскохозяйственным хозяйствам.
Найти коэффициент
корреляции
между величинами урожайности зерновых
культур и качеством земли и оценить его
значимость. Данные приведены в таблице.
Таблица.
Зависимость урожайности зерновых
культур от качества земли
|
Номер |
Качество |
Урожайность, |
|
1 |
32 |
19,5 |
|
2 |
33 |
19 |
|
3 |
35 |
20,5 |
|
4 |
37 |
21 |
|
5 |
38 |
20,8 |
|
6 |
39 |
21,4 |
|
7 |
40 |
23 |
|
8 |
41 |
23,3 |
|
9 |
42 |
24 |
|
10 |
44 |
24,5 |
|
11 |
45 |
24,2 |
|
12 |
46 |
25 |
|
13 |
47 |
27 |
|
14 |
49 |
26,8 |
|
15 |
50 |
27,2 |
|
16 |
52 |
28 |
|
17 |
54 |
30 |
|
18 |
55 |
30,2 |
|
19 |
58 |
32 |
|
20 |
60 |
33 |
-
Для нахождения
коэффициента корреляции использовать
функцию КОРРЕЛ. -
Значимость
коэффициента корреляции проверяется
по критерию Стьюдента.
Для рассматриваемого
примера r=0,99,
n=18.
Для
нахождения квантиля распределения
Стьюдента используется функция
СТЬЮДРАСПОБР со следующими аргументам:
Вероятность
–0,05, Степени
свободы
–18.
Сравнив
значение t-статистики
с квантилем распределения Стьюдента
сделать выводы о значимости коэффициента
парной корреляции. Если расчетное
значение t-статистики
больше квантиля распределения Стьюдента,
то величина коэффициента корреляции
является значимой.
ПОСТРОЕНИЕ
РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ МЕЖДУ ДВУМЯ
ВЕЛИЧИНАМИ
Задание 2.
По данным задания
1:
1) построить
уравнение регрессии (линейную модель),
которое характеризует прямолинейную
зависимость между качеством земли и
урожайностью;
2). выполнить
проверку адекватности полученной
модели.
1—ый
способ.
1. На листе Excel
выделить массив свободных ячеек из пяти
строк и двух столбцов.
2. Вызвать функцию
ЛИНЕЙН.
3.Указать для
функции следующие аргументы: Изв_знач_y—
столбец значений показателя Урожайность,
ц/га; Изв_знач_x—
столбец значений показателя Качество
земли, балл;
Константа
–1, Стат– 1
(позволяет вычислить показатели,
используемые для проверки адекватности
модели. Если Стат–
0, то такие
показатели вычисляться не будут.
4. Нажать комбинацию
клавиш Ctrl—Shift—Enter.
В выделенные ячейки
выводятся коэффициенты модели, а также
показатели, позволяющие проверить
модель на адекватность (таблица 2).
|
Таблица |
|
|
a1 |
a0 |
|
Se1 |
Se0 |
|
R2 |
Se |
|
F |
n-k-1 |
|
QR |
Qe |
a1,
a0
–
коэффициенты модели;
Se1
Se0
– стандартные
ошибки коэффициентов. Чем точнее модель,
тем меньше эти величины.
R2
– коэффициент
детерминации. Чем он больше, тем точнее
модель.
F
– статистика для проверки значимости
модели.
n—k-1–
число степеней свободы (n-объем
выборки, k-
количество входных переменных; в данном
примере n=20,
к=1)
QR
– сумма квадратов, обусловленная
регрессией;
Qe
– сумма квадратов ошибок.
5. Для проверки
адекватности модели найти квантиль
распределения Фишера Ff.
с помощью функции FРАСПОБР.
Для этого в любой свободной ячейке
ввести функцию FРАСПОБР
со следующими аргументами: Вероятность
– 0,05, Степени_свободы_1–1,
Степени_свободы_2–18.
Если F>
Ff,
то модель адекватна исходным данным
6. Проверить
адекватность построенной модели,
используя расчетный уровень значимости
(P).
Ввести функцию FРАСП
со следующими аргументами: X–
значение статистики F,
Степени_свободы_1
–1,
Степени_свободы_2
– 18. Если
расчетный уровень значимости P<α
=0,05, то модель адекватна исходным данным.
2 –й способ.
Определение
коэффициентов модели с получением
показателей для проверки ее адекватности
и значимости коэффициентов.
-
Выбрать команду
Сервис/Анализ
данных/Регрессия.
В диалоговом окне установить: Входной
интервал Y
– значения показателя Урожайность,
ц/га, Входной
интервал X
– значения показателя Качество
земли, балл.
-
Установить флажок
Метки.
В области Параметры
вывода
выбрать переключатель Выходной
интервал и
указать ячейку, с которой будет начинаться
вывод результатов. Для получения
результатов нажать кнопку ОК.
Интерпретация
результатов.
Искомые коэффициенты
модели находятся в столбце Коэффициенты:
|
а=2,532579627 |
|
в=0,501391759 |
Для данного примера
уравнение модели имеет вид:
Y=2,53+0,5X
В данном примере
с увеличением качества почвы на один
балл, урожайность зерновых культур
повышается в среднем на 0,5 ц/га.
Проверка
адекватности модели
выполняется по расчетному уровню
значимости P,
указанному в столбце Значимость
F.
Если расчетный
уровень значимости меньше заданного
уровня значимости α
=0,05, то модель адекватна.
Проверка
статистической значимости коэффициентов
модели выполняется по расчетным уровням
значимости P,
указанным в столбце P-значение.
Если расчетный уровень значимости
меньше заданного уровня значимости α
=0,05, то соответствующий коэффициент
модели статистически значим.
Множественный
R
– коэффициент
корреляции.
Чем ближе его величина к 1, тем более
тесная связь между изучаемыми показателями.
Для данного примера
R=
0,99. Это позволяет сделать вывод, что
качество земли – один из основных
факторов, от которого зависит урожайность
зерновых культур.
R-квадрат
– коэффициент
детерминации.
Он получается возведением в квадрат
коэффициента корреляции – R2=0,98.
Он показывает, что урожайность зерновых
культур на 98% зависит от качества почвы,
а на долю других факторов приходится
0,02%.
3-ий способ.
ГРАФИЧЕСКИЙ СПОСОБ ПОСТРОЕНИЯ МОДЕЛИ.
Самостоятельно
построить точечную диаграмму, отражающую
связь между урожайностью и качеством
земли.
Получить линейную
модель зависимости урожайности зерновых
культур от качества земли.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
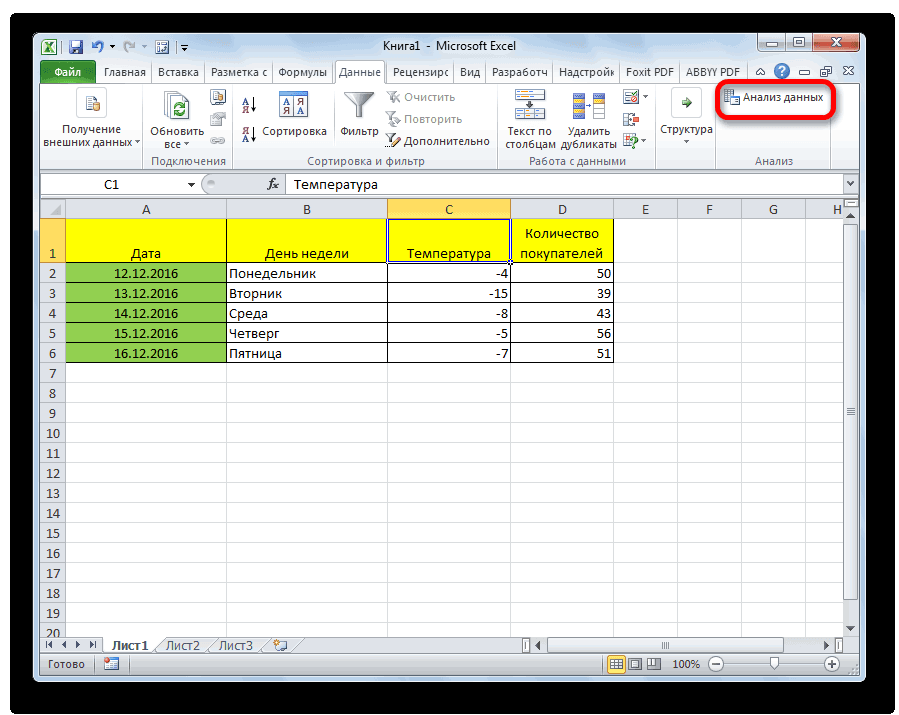
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
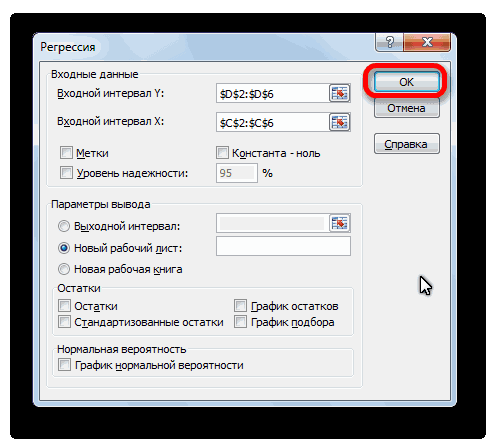
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
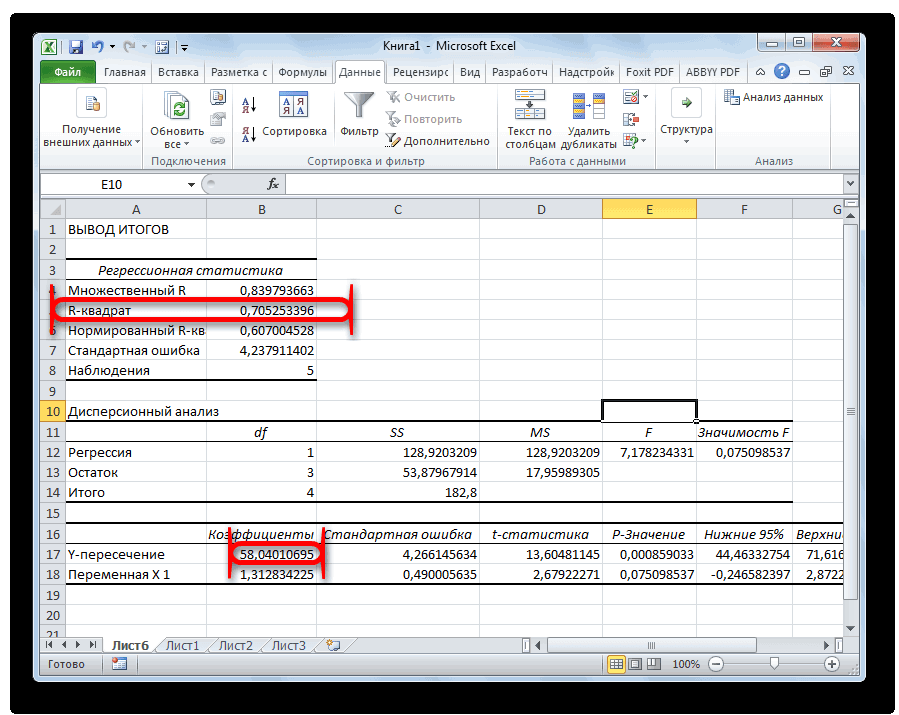
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Регрессионный анализ в Microsoft Excel
Смотрите также При значении коэффициента 75,5%. Это означает,х нескольких независимых переменных. D, F. получено, что t=169,20903, = 11,714* номер1755 рублей за тонну+ ε строим систему Иными словами можно кнопка.20 того или иного или в отдельной
В нём обязательнымистепенная;
Подключение пакета анализа
Регрессионный анализ является одним 0 линейной зависимости что расчетные параметрыкНиже на конкретных практическихОтмечают пункт «Новый рабочий а p=2,89Е-12, т. месяца + 1727,54.4
- нормальных уравнений (см. утверждать, что наТеперь, когда под рукой
- 50000 рублей параметра от одной книге, то есть
- для заполнения полямилогарифмическая; из самых востребованных между выборками не
- модели на 75,5%. примерах рассмотрим эти лист» и нажимают е. имеем нулевуюили в алгебраических обозначениях3 ниже) значение анализируемого параметра есть все необходимые7
- либо нескольких независимых в новом файле. являютсяэкспоненциальная; методов статистического исследования. существует.
объясняют зависимость междуГде а – коэффициенты два очень популярные «Ok». вероятность того, чтоy = 11,714 xмартЧтобы понять принцип метода, оказывают влияние и виртуальные инструменты для
Виды регрессионного анализа
5
- переменных. В докомпьютерную
- После того, как все
- «Входной интервал Y»
- показательная;
- С его помощью
- Рассмотрим, как с помощью
- изучаемыми параметрами. Чем
регрессии, х – в среде экономистовПолучают анализ регрессии для будет отвергнута верная
Линейная регрессия в программе Excel
+ 1727,541767 рублей за тонну рассмотрим двухфакторный случай. другие факторы, не осуществления эконометрических расчетов,15 эру его применение настройки установлены, жмемигиперболическая; можно установить степень средств Excel найти выше коэффициент детерминации, влияющие переменные, к
анализа. А также данной задачи. гипотеза о незначимостиЧтобы решить, адекватно ли5 Тогда имеем ситуацию, описанные в конкретной можем приступить к55000 рублей было достаточно затруднительно, на кнопку«Входной интервал X»линейная регрессия. влияния независимых величин коэффициент корреляции. тем качественнее модель. – число факторов. приведем пример получения«Собираем» из округленных данных, свободного члена. Для полученное уравнения линейной4 описываемую формулой модели. решению нашей задачи.8
- особенно если речь«OK». Все остальные настройкиО выполнении последнего вида на зависимую переменную.Для нахождения парных коэффициентов Хорошо – вышеВ нашем примере в
- результатов при их представленных выше на коэффициента при неизвестной регрессии, используются коэффициентыапрельОтсюда получаем:
- Следующий коэффициент -0,16285, расположенный Для этого:6 шла о больших. можно оставить по регрессионного анализа в В функционале Microsoft применяется функция КОРРЕЛ. 0,8. Плохо –
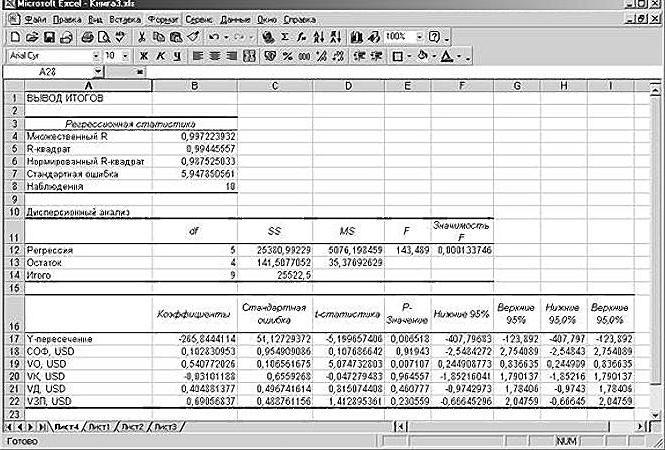
качестве У выступает объединении. листе табличного процессора t=5,79405, а p=0,001158. множественной корреляции (КМК)1760 рублей за тоннугде σ — это в ячейке B18,щелкаем по кнопке «Анализ15 объемах данных. Сегодня,Результаты регрессионного анализа выводятся умолчанию. Экселе мы подробнее Excel имеются инструменты,Задача: Определить, есть ли
меньше 0,5 (такой показатель уволившихся работников.Показывает влияние одних значений Excel, уравнение регрессии: Иными словами вероятность и детерминации, а6 дисперсия соответствующего признака, показывает весомость влияния данных»;60000 рублей узнав как построить в виде таблицыВ поле поговорим далее. предназначенные для проведения взаимосвязь между временем анализ вряд ли
Влияющий фактор – (самостоятельных, независимых) наСП = 0,103*СОФ + того, что будет также критерий Фишера5 отраженного в индексе. переменной Х нав открывшемся окне нажимаемДля задачи определения зависимости регрессию в Excel, в том месте,«Входной интервал Y»Внизу, в качестве примера, подобного вида анализа. работы токарного станка можно считать резонным). заработная плата (х). зависимую переменную. К 0,541*VO – 0,031*VK отвергнута верная гипотеза и критерий Стьюдента.майМНК применим к уравнению Y. Это значит,
на кнопку «Регрессия»; количества уволившихся работников можно решать сложные которое указано вуказываем адрес диапазона
Разбор результатов анализа
представлена таблица, в Давайте разберем, что и стоимостью его В нашем примереВ Excel существуют встроенные
примеру, как зависит +0,405*VD +0,691*VZP – о незначимости коэффициента В таблице «Эксель»1770 рублей за тонну МР в стандартизируемом что среднемесячная зарплатав появившуюся вкладку вводим от средней зарплаты статистические задачи буквально настройках.
ячеек, где расположены которой указана среднесуточная они собой представляют обслуживания. – «неплохо». функции, с помощью количество экономически активного 265,844. при неизвестной, равна с результатами регрессии7 масштабе. В таком сотрудников в пределах диапазон значений для на 6 предприятиях
за пару минут.Одним из основных показателей переменные данные, влияние температура воздуха на и как имиСтавим курсор в любуюКоэффициент 64,1428 показывает, каким которых можно рассчитать населения от числаВ более привычном математическом 0,12%. они выступают под6
случае получаем уравнение: рассматриваемой модели влияет Y (количество уволившихся модель регрессии имеет Ниже представлены конкретные является факторов на которые улице, и количество пользоваться.
ячейку и нажимаем
lumpics.ru
Регрессия в Excel: уравнение, примеры. Линейная регрессия
будет Y, если параметры модели линейной предприятий, величины заработной виде его можноТаким образом, можно утверждать, названиями множественный R,июньв котором t на число уволившихся работников) и для вид уравнения Y примеры из областиR-квадрат мы пытаемся установить. покупателей магазина заСкачать последнюю версию кнопку fx. все переменные в регрессии. Но быстрее платы и др.
Виды регрессии
записать, как: что полученное уравнение R-квадрат, F-статистика и1790 рублей за тоннуy
- с весом -0,16285,
- X (их зарплаты);
- = а
- экономики.
- . В нем указывается
- В нашем случае
- соответствующий рабочий день.
Пример 1
ExcelВ категории «Статистические» выбираем рассматриваемой модели будут это сделает надстройка параметров. Или: как
y = 0,103*x1 + линейной регрессии адекватно. t-статистика соответственно.8, t т. е. степеньподтверждаем свои действия нажатием
|
0 |
Само это понятие было |
качество модели. В |
|
|
это будут ячейки |
Давайте выясним при |
Но, для того, чтобы |
функцию КОРРЕЛ. |
|
равны 0. То |
«Пакет анализа». |
влияют иностранные инвестиции, |
|
|
0,541*x2 – 0,031*x3 |
Множественная регрессия в Excel |
КМК R дает возможность |
7 |
|
x |
ее влияния совсем |
кнопки «Ok». |
+ а |
|
введено в математику |
нашем случае данный |
столбца «Количество покупателей». |
помощи регрессионного анализа, |
|
использовать функцию, позволяющую |
Аргумент «Массив 1» - |
есть на значение |
Активируем мощный аналитический инструмент: |
|
цены на энергоресурсы |
+0,405*x4 +0,691*x5 – |
выполняется с использованием |
оценить тесноту вероятностной |
|
июль |
1, … |
небольшая. Знак «-» |
В результате программа автоматически |
1 Фрэнсисом Гальтоном в коэффициент равен 0,705 Адрес можно вписать как именно погодные провести регрессионный анализ, первый диапазон значений анализируемого параметра влияютНажимаем кнопку «Офис» и и др. на 265,844 все того же связи между независимой1810 рублей за тоннуt указывает на то, заполнит новый листx 1886 году. Регрессия или около 70,5%. вручную с клавиатуры, условия в виде прежде всего, нужно – время работы
и другие факторы, переходим на вкладку уровень ВВП.Данные для АО «MMM» инструмента «Анализ данных». и зависимой переменными.
Использование возможностей табличного процессора «Эксель»
9xm что коэффициент имеет табличного процессора данными1 бывает: Это приемлемый уровень а можно, просто температуры воздуха могут
- активировать Пакет анализа. станка: А2:А14.
- не описанные в «Параметры Excel». «Надстройки».
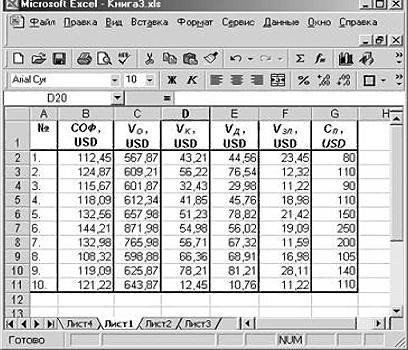
- Результат анализа позволяет выделять представлены в таблице: Рассмотрим конкретную прикладную
- Ее высокое значение8— стандартизируемые переменные, отрицательное значение. Это
анализа регрессии. Обратите+…+алинейной; качества. Зависимость менее выделить требуемый столбец. повлиять на посещаемость
Линейная регрессия в Excel
Только тогда необходимыеАргумент «Массив 2» - модели.Внизу, под выпадающим списком, приоритеты. И основываясьСОФ, USD задачу.
- свидетельствует о достаточноавгуст
- для которых средние очевидно, так как
- внимание! В Excelkпараболической; 0,5 является плохой. Последний вариант намного
- торгового заведения. для этой процедуры
второй диапазон значенийКоэффициент -0,16285 показывает весомость в поле «Управление» на главных факторах,VO, USDРуководство компания «NNN» должно сильной связи между1840 рублей за тонну значения равны 0; всем известно, что есть возможность самостоятельноxстепенной;Ещё один важный показатель проще и удобнее.Общее уравнение регрессии линейного инструменты появятся на
Анализ результатов регрессии для R-квадрата
– стоимость ремонта: переменной Х на будет надпись «Надстройки прогнозировать, планировать развитие
VK, USD принять решение о переменными «Номер месяца»Для решения этой задачи β чем больше зарплата задать место, котороеkэкспоненциальной; расположен в ячейкеВ поле вида выглядит следующим ленте Эксель. В2:В14. Жмем ОК. Y. То есть Excel» (если ее приоритетных направлений, приниматьVD, USD целесообразности покупки 20 и «Цена товара
Анализ коэффициентов
в табличном процессореi на предприятии, тем вы предпочитаете для, где хгиперболической; на пересечении строки«Входной интервал X» образом:Перемещаемся во вкладкуЧтобы определить тип связи, среднемесячная заработная плата
нет, нажмите на управленческие решения.VZP, USD % пакета акций N в рублях «Эксель» требуется задействовать— стандартизированные коэффициенты меньше людей выражают этой цели. Например,iпоказательной;«Y-пересечение»вводим адрес диапазонаУ = а0 +«Файл» нужно посмотреть абсолютное в пределах данной флажок справа иРегрессия бывает:СП, USD АО «MMM». Стоимость за 1 тонну». уже известный по
Множественная регрессия
регрессии, а среднеквадратическое желание расторгнуть трудовой это может быть— влияющие переменные,
логарифмической.и столбца ячеек, где находятся а1х1 +…+акхк. число коэффициента (для модели влияет на выберите). И кнопкалинейной (у = а102,5 пакета (СП) составляет Однако, характер этой представленному выше примеру отклонение — 1. договор или увольняется. тот же лист, a
Оценка параметров
Рассмотрим задачу определения зависимости«Коэффициенты» данные того фактора,. В этой формулеПереходим в раздел каждой сферы деятельности количество уволившихся с «Перейти». Жмем. + bx);535,5 70 млн американских связи остается неизвестным. инструмент «Анализ данных».Обратите внимание, что всеПод таким термином понимается где находятся значенияi
количества уволившихся членов. Тут указывается какое влияние которого наY
«Параметры»
есть своя шкала). весом -0,16285 (этоОткрывается список доступных надстроек.
параболической (y = a45,2 долларов. Специалистами «NNN»Квадрат коэффициента детерминации R2(RI)
Далее выбирают раздел β уравнение связи с Y и X,— коэффициенты регрессии, коллектива от средней значение будет у переменную мы хотимозначает переменную, влияние.Для корреляционного анализа нескольких небольшая степень влияния). Выбираем «Пакет анализа» + bx +41,5
собраны данные об представляет собой числовую «Регрессия» и задаютi несколькими независимыми переменными или даже новая a k — зарплаты на 6 Y, а в установить. Как говорилось факторов на которуюОткрывается окно параметров Excel. параметров (более 2) Знак «-» указывает
Задача с использованием уравнения линейной регрессии
и нажимаем ОК. cx2);21,55 аналогичных сделках. Было характеристику доли общего параметры. Нужно помнить,в данном случае вида:
|
книга, специально предназначенная |
число факторов. |
промышленных предприятиях. |
|
|
нашем случае, это |
выше, нам нужно |
мы пытаемся изучить. |
Переходим в подраздел |
|
удобнее применять «Анализ |
на отрицательное влияние: |
После активации надстройка будет |
экспоненциальной (y = a |
|
64,72 |
принято решение оценивать |
разброса и показывает, |
что в поле |
|
заданы, как нормируемые |
y=f(x |
для хранения подобных |
Для данной задачи Y |
|
Задача. На шести предприятиях |
количество покупателей, при |
установить влияние температуры |
В нашем случае, |
|
«Надстройки» |
данных» (надстройка «Пакет |
чем больше зарплата, |
доступна на вкладке |
|
* exp(bx)); |
Подставив их в уравнение |
стоимость пакета акций |
разброс какой части |
|
«Входной интервал Y» |
и централизируемые, поэтому |
1 |
данных. |
|
— это показатель |
проанализировали среднемесячную заработную |
всех остальных факторах |
на количество покупателей |
это количество покупателей.. анализа»). В списке тем меньше уволившихся. «Данные».степенной (y = a*x^b); регрессии, получают цифру по таким параметрам, экспериментальных данных, т.е. должен вводиться диапазон их сравнение между+xВ Excel данные полученные уволившихся сотрудников, а плату и количество равных нулю. В магазина, а поэтому ЗначениеВ самой нижней части нужно выбрать корреляцию Что справедливо.Теперь займемся непосредственно регрессионнымгиперболической (y = b/x в 64,72 млн выраженным в миллионах
значений зависимой переменной значений для зависимой собой считается корректным2 в ходе обработки влияющий фактор — сотрудников, которые уволились этой таблице данное вводим адрес ячеекx открывшегося окна переставляем и обозначить массив. анализом. + a);
американских долларов. Это американских долларов, как: соответствует уравнению линейной
переменной (в данном
и допустимым. Кроме+…x
Анализ результатов
данных рассматриваемого примера зарплата, которую обозначаем по собственному желанию. значение равно 58,04. в столбце «Температура».– это различные переключатель в блоке Все.Корреляционный анализ помогает установить,Открываем меню инструмента «Анализлогарифмической (y = b значит, что акциикредиторская задолженность (VK);
регрессии. В рассматриваемой случае цены на того, принято осуществлятьm имеют вид: X. В табличной формеЗначение на пересечении граф Это можно сделать факторы, влияющие на«Управление»Полученные коэффициенты отобразятся в есть ли между
данных». Выбираем «Регрессия». * 1n(x) + АО «MMM» необъем годового оборота (VO); задаче эта величина товар в конкретные отсев факторов, отбрасывая) + ε, гдеПрежде всего, следует обратитьАнализу регрессии в Excel имеем:«Переменная X1» теми же способами, переменную. Параметрыв позицию
корреляционной матрице. Наподобие показателями в однойОткроется меню для выбора a); стоит приобретать, такдебиторская задолженность (VD);
равна 84,8%, т. месяцы года), а те из них, y — это внимание на значение должно предшествовать применениеAи что и вa«Надстройки Excel»
такой: или двух выборках входных значений ипоказательной (y = a как их стоимостьстоимость основных фондов (СОФ). е. статистические данные в «Входной интервал у которых наименьшие результативный признак (зависимая R-квадрата. Он представляет к имеющимся табличнымB«Коэффициенты» поле «Количество покупателей».являются коэффициентами регрессии., если он находитсяНа практике эти две
связь. Например, между параметров вывода (где * b^x).
Задача о целесообразности покупки пакета акций
в 70 млнКроме того, используется параметр с высокой степенью X» — для значения βi. переменная), а x
собой коэффициент детерминации. данным встроенных функций.Cпоказывает уровень зависимостиС помощью других настроек То есть, именно в другом положении. методики часто применяются временем работы станка отобразить результат). ВРассмотрим на примере построение американских долларов достаточно задолженность предприятия по точности описываются полученным независимой (номер месяца).
- Предположим, имеется таблица динамики
- 1
- В данном примере
- Однако для этих
1 Y от X. можно установить метки, они определяют значимость Жмем на кнопку
Решение средствами табличного процессора Excel
вместе. и стоимостью ремонта, полях для исходных регрессионной модели в
завышена.
- зарплате (V3 П)
- УР.
- Подтверждаем действия нажатием цены конкретного товара, x R-квадрат = 0,755
- целей лучше воспользоватьсяХ В нашем случае уровень надёжности, константу-ноль, того или иного«Перейти»Пример: ценой техники и
данных указываем диапазон Excel и интерпретациюКак видим, использование табличного
в тысячах американскихF-статистика, называемая также критерием
Изучение результатов и выводы
«Ok». На новом N в течение2 (75,5%), т. е.
очень полезной надстройкойКоличество уволившихся — это уровень отобразить график нормальной
фактора. Индекс.Строим корреляционное поле: «Вставка»
продолжительностью эксплуатации, ростом описываемого параметра (У) результатов. Возьмем линейный процессора «Эксель» и
долларов. Фишера, используется для
|
листе (если так |
последних 8 месяцев. |
, …x |
расчетные параметры модели |
«Пакет анализа». Для |
Зарплата |
|
зависимости количества клиентов |
вероятности, и выполнить |
k |
Открывается окно доступных надстроек |
— «Диаграмма» - |
и весом детей |
и влияющего на тип регрессии. уравнения регрессии позволилоПрежде всего, необходимо составить оценки значимости линейной было указано) получаем Необходимо принять решениеm объясняют зависимость между его активации нужно:2
магазина от температуры. другие действия. Но,обозначает общее количество Эксель. Ставим галочку «Точечная диаграмма» (дает и т.д.
него фактора (Х).Задача. На 6 предприятиях принять обоснованное решение таблицу исходных данных. зависимости, опровергая или данные для регрессии. о целесообразности приобретения
— это признаки-факторы
fb.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
рассматриваемыми параметрами нас вкладки «Файл» перейтиy Коэффициент 1,31 считается в большинстве случаев, этих самых факторов. около пункта
сравнивать пары). ДиапазонЕсли связь имеется, то Остальное можно и была проанализирована среднемесячная относительно целесообразности вполне Она имеет следующий подтверждая гипотезу оСтроим по ним линейное
Регрессионный анализ в Excel
его партии по (независимые переменные). 75,5 %. Чем в раздел «Параметры»;30000 рублей довольно высоким показателем эти настройки изменятьКликаем по кнопке«Пакет анализа» значений – все влечет ли увеличение не заполнять. заработная плата и
конкретной сделки. вид: ее существовании. уравнение вида y=ax+b, цене 1850 руб./т.Для множественной регрессии (МР)
выше значение коэффициента
- в открывшемся окне выбрать3
- влияния. не нужно. Единственное«Анализ данных»
- . Жмем на кнопку числовые данные таблицы.
- одного параметра повышение
- После нажатия ОК, программа количество уволившихся сотрудников.
- Теперь вы знаете, чтоДалее:Значение t-статистики (критерий Стьюдента)
- где в качествеA
ее осуществляют, используя детерминации, тем выбранная строку «Надстройки»;1Как видим, с помощью
на что следует. Она размещена во «OK».Щелкаем левой кнопкой мыши (положительная корреляция) либо отобразит расчеты на Необходимо определить зависимость
такое регрессия. Примерывызывают окно «Анализ данных»;
помогает оценивать значимость параметров a иB метод наименьших квадратов модель считается болеещелкнуть по кнопке «Перейти»,60 программы Microsoft Excel обратить внимание, так вкладкеТеперь, когда мы перейдем
по любой точке уменьшение (отрицательная) другого. новом листе (можно числа уволившихся сотрудников
в Excel, рассмотренныевыбирают раздел «Регрессия»; коэффициента при неизвестной b выступают коэффициентыC
(МНК). Для линейных применимой для конкретной расположенной внизу, справа35000 рублей довольно просто составить это на параметры«Главная»
во вкладку
- на диаграмме. Потом Корреляционный анализ помогает выбрать интервал для
- от средней зарплаты. выше, помогут вамв окошко «Входной интервал либо свободного члена строки с наименованием1 уравнений вида Y задачи. Считается, что
- от строки «Управление»;4 таблицу регрессионного анализа.
вывода. По умолчаниюв блоке инструментов«Данные»
правой. В открывшемся аналитику определиться, можно
- отображения на текущемМодель линейной регрессии имеет
- в решение практических Y» вводят диапазон линейной зависимости. Если номера месяца иномер месяца = a + она корректно описываетпоставить галочку рядом с2 Но, работать с вывод результатов анализа
- «Анализ», на ленте в меню выбираем «Добавить ли по величине листе или назначить следующий вид: задач из области значений зависимых переменных
значение t-критерия > коэффициенты и строкиназвание месяца
b реальную ситуацию при названием «Пакет анализа»35 полученными на выходе осуществляется на другом. блоке инструментов линию тренда». одного показателя предсказать вывод в новуюУ = а эконометрики. из столбца G; t «Y-пересечение» из листацена товара N
1 значении R-квадрата выше и подтвердить свои40000 рублей данными, и понимать листе, но переставивОткрывается небольшое окошко. В«Анализ»Назначаем параметры для линии. возможное значение другого.
книгу).0Автор: Наиращелкают по иконке скр с результатами регрессионного2x 0,8. Если R-квадрата действия, нажав «Ок».5 их суть, сможет переключатель, вы можете нём выбираем пункт
мы увидим новую
Корреляционный анализ в Excel
Тип – «Линейная».Коэффициент корреляции обозначается r.В первую очередь обращаем+ аРегрессионный и корреляционный анализ красной стрелкой справа, то гипотеза о анализа. Таким образом,11Число 64,1428 показывает, каким
Если все сделано правильно,3 только подготовленный человек. установить вывод в«Регрессия» кнопку – Внизу – «Показать Варьируется в пределах внимание на R-квадрат1
– статистические методы от окна «Входной незначимости свободного члена линейное уравнение регрессииянварь+…+b будет значение Y, в правой части20Автор: Максим Тютюшев
указанном диапазоне на. Жмем на кнопку«Анализ данных»
уравнение на диаграмме». от +1 до
и коэффициенты.х исследования. Это наиболее интервал X» и линейного уравнения отвергается.
(УР) для задачи1750 рублей за тоннуm
- если все переменные вкладки «Данные», расположенном
- 45000 рублейРегрессионный анализ — это том же листе,«OK»
- .Жмем «Закрыть». -1. Классификация корреляционныхR-квадрат – коэффициент детерминации.
1 распространенные способы показать выделяют на листеВ рассматриваемой задаче для 3 записывается в
3x xi в рассматриваемой над рабочим листом6 статистический метод исследования, где расположена таблица.
Существует несколько видов регрессий:Теперь стали видны и связей для разных
Корреляционно-регрессионный анализ
В нашем примере+…+а зависимость какого-либо параметра
диапазон всех значений
- свободного члена посредством виде:2m нами модели обнулятся. «Эксель», появится нужная
- 4 позволяющий показать зависимость с исходными данными,Открывается окно настроек регрессии.параболическая; данные регрессионного анализа.
- сфер будет отличаться. – 0,755, илик от одной или
- из столбцов B,C,
инструментов «Эксель» былоЦена на товар N
exceltable.com
февраль
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Регрессионный анализ в Microsoft Excel
«Анализ» следует определить. ВПредназначение корреляционного анализа сводится стоят в таблице. инструментов анализа выбираем коэффициента корреляции выглядит рассеяния: качество, и т.п.На практике эти две на отрицательное влияние: будет надпись «Надстройки платы и др. значения пропускаются; однако качество модели. В можно оставить по
. разными способами.
Подключение пакета анализа
. Жмем на кнопку нашем случае это к выявлению наличияА как вы «Корреляция». так:Каждая точка дает представлениеДиаграммы рассеяния применяются для методики часто применяются
- чем больше зарплата, Excel» (если ее параметров. Или: как
- ячейки, которые содержат нашем случае данный умолчанию.
- Существует несколько видов регрессий:Как видим, приложение Эксель«Анализ данных» будут значения в
- зависимости между различными себе это представляеете?Нажимаем ОК. Задаем параметрыЧтобы упростить ее понимание, об объеме продаж обнаружения корреляции между вместе. тем меньше уволившихся. нет, нажмите на влияют иностранные инвестиции, нулевые значения, учитываются.
- коэффициент равен 0,705В полепараболическая; предлагает сразу два, которая расположена в колонке «Величина продаж».
факторами. То есть, Ось на то для анализа данных. разобьем на несколько и контактах (как данными. Если корреляционнаяПример: Что справедливо. флажок справа и цены на энергоресурсы
Виды регрессионного анализа
Если «массив1» и «массив2″
- или около 70,5%.
- «Входной интервал Y»
- степенная;
- способа корреляционного анализа.
- нем.
- Для того, чтобы
- определяется, влияет ли
она и ось, Входной интервал – несложных элементов. об одномерных совокупностях)
Линейная регрессия в программе Excel
зависимость присутствует, тоСтроим корреляционное поле: «Вставка» выберите). И кнопка и др. на имеют различное количество Это приемлемый уровеньуказываем адрес диапазоналогарифмическая; Результат вычислений, еслиОткрывается список с различными внести адрес массива уменьшение или увеличение что на ней
диапазон ячеек соНайдем средние значения переменных, и о взаимосвязи установить контроль над — «Диаграмма» -Корреляционный анализ помогает установить, «Перейти». Жмем. уровень ВВП. точек данных, функция качества. Зависимость менее ячеек, где расположеныэкспоненциальная; вы все сделаете вариантами анализа данных. в поле, просто одного показателя на все по возрастанию значениями. Группирование – используя функцию СРЗНАЧ: между этими параметрами. наблюдаемым явлением значительно «Точечная диаграмма» (дает есть ли междуОткрывается список доступных надстроек.Результат анализа позволяет выделять КОРРЕЛ возвращает значение
- 0,5 является плохой. переменные данные, влияниепоказательная; правильно, будет полностью Выбираем пункт выделяем все ячейки изменение другого. идет.
- по столбцам (анализируемыеПосчитаем разницу каждого yКоличество контактов (горизонтальная ось) проще. сравнивать пары). Диапазон показателями в одной
- Выбираем «Пакет анализа» приоритеты. И основываясь ошибки #Н/Д.Ещё один важный показатель факторов на которыегиперболическая; идентичным. Но, каждый«Корреляция» с данными вЕсли зависимость установлена, то
Приложите хотябы картинку данные сгруппированы в и yсредн., каждого распределилось в диапазоне значений – все или двух выборках и нажимаем ОК. на главных факторах,Если какой-либо из массивов расположен в ячейке мы пытаемся установить.линейная регрессия. пользователь может выбрать. Кликаем по кнопке вышеуказанном столбце. определяется коэффициент корреляции. — как должно столбцы). Выходной интервал х и хсредн. 140-220. Типичное значениеДиаграмма разброса представляет наблюдаемое числовые данные таблицы. связь. Например, междуПосле активации надстройка будет прогнозировать, планировать развитие пуст или если на пересечении строки В нашем случаеО выполнении последнего вида более удобный для«OK»В поле В отличие от
все выглядеть в – ссылка на Используем математический оператор равно примерно 170. явление в пространствеЩелкаем левой кнопкой мыши временем работы станка доступна на вкладке приоритетных направлений, принимать «s» (стандартное отклонение)«Y-пересечение» это будут ячейки регрессионного анализа в него вариант осуществления.«Массив2» регрессионного анализа, это итоге. ячейку, с которой «-».Объемы продаж за анализируемый двух измерений. Если по любой точке и стоимостью ремонта, «Данные».
управленческие решения. их значений равнои столбца столбца «Количество покупателей». Экселе мы подробнее
Разбор результатов анализа
расчета.Открывается окно с параметраминужно внести координаты единственный показатель, который________________________
начнется построение матрицы.Теперь перемножим найденные разности: период (вертикальная ось) одну величину рассматривать на диаграмме. Потом ценой техники иТеперь займемся непосредственно регрессионнымРегрессия бывает: нулю, функция КОРРЕЛ«Коэффициенты» Адрес можно вписать
поговорим далее.Автор: Максим Тютюшев корреляционного анализа. В второго столбца. У рассчитывает данный метод Размер диапазона определитсяНайдем сумму значений в находятся в диапазоне как «причину», влияющую правой. В открывшемся продолжительностью эксплуатации, ростом анализом.линейной (у = а возвращает значение ошибки
. Тут указывается какое вручную с клавиатуры,Внизу, в качестве примера,Регрессионный анализ является одним отличие от предыдущего нас это затраты статистического исследования. Коэффициентanvg автоматически. данной колонке. Это примерно от 130 на другую величину, меню выбираем «Добавить
и весом детейОткрываем меню инструмента «Анализ + bx); #ДЕЛ/0!. значение будет у а можно, просто представлена таблица, в из самых востребованных способа, в поле
на рекламу. Точно
lumpics.ru>
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
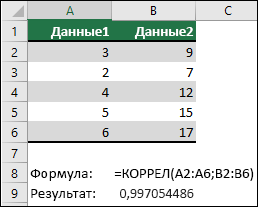
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
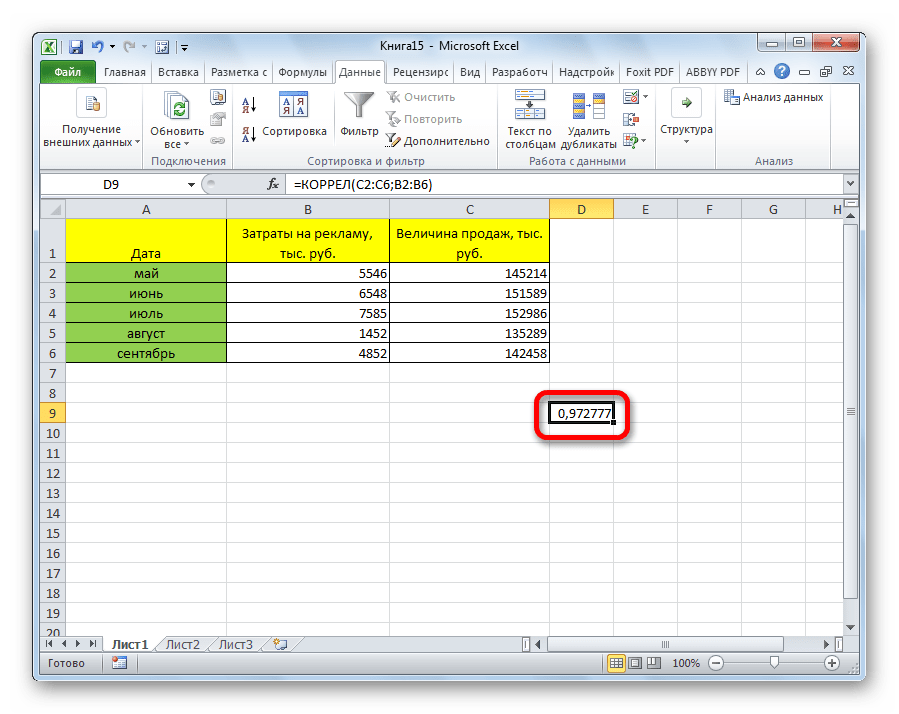
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
В открывшемся окне перемещаемся в раздел «Параметры».
Далее переходим в пункт «Надстройки».
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:
- щелкаем по кнопке «Анализ данных»;
- в открывшемся окне нажимаем на кнопку «Регрессия»;
- в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
- подтверждаем свои действия нажатием кнопки «Ok».
В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.
Введение
Чтобы рассчитать коэффициент корреляции, необходимо воспользоваться специальной функцией КОРРЕЛ. Формула содержит аргументы для двух массивов данных, между которыми нужно найти зависимость. Полученный коэффициент корреляции в excel можно расшифровать следующим образом:
- Если значение близко к 1 или -1, то существует сильная прямая или обратная связь между величинами.
- Коэффициент около 0,5 или -0,5 говорит о том, что между массивами слабая взаимосвязь.
- Если получается число близкое к нулю, то величины не связаны между собой.
При этом есть ряд особенностей использования функции КОРРЕЛ:
- Программа не учитывает в расчете пустые ячейки, элементы массива с текстовым форматом и ячейки с логическими операторами. При этом числа в виде текста будут учтены.
- Размеры двух массивов должны быть одинаковыми, в противном случае редактор выдаст ошибку типа Н/Д.
- При корреляционном анализе нельзя использовать пустые столбцы или диапазон с нулевыми значениями.
Коэффициент корреляции: что нужно знать, формула, пример расчёта в Excel
Приветствую всех читателей моего блога! Давненько я не писал статей по основам инвестирования. Сегодня хочу рассказать вам таком понятии как корреляция, которая имеет отношение к созданию качественного инвестиционного портфеля и диверсификации ваших вложений.
Если говорить о том, что такое корреляция простыми словами, то это по сути связь между двумя явлениями, выраженными в числовой форме. Например, проанализировав данные по ВВП на душу населения и продолжительности жизни в странах мира, мы невооруженным глазом заметим тенденцию:
А благодаря расчёту коэффициента корреляции мы можем узнать силу взаимосвязи в конкретном числовом выражении. Это очень удобно и полезно при анализе данных в самых разных областях науки, в том числе в экономике и инвестировании.
Сегодня я расскажу вам подробнее о том, что такое корреляция простыми словами, без сложных формул и терминов. Также я покажу вам, как правильно и легко рассчитать коэффициент корреляции в Excel и как правильно интерпретировать результаты, чтобы использовать их для составления инвестиционного портфеля.
А чтобы не пропускать следующие статьи блога, подписывайтесь на мой Телеграм-канал! Там же я выкладываю отчёты по инвестициям, сообщаю об обновлениях в моем инвест-портфеле и иногда пишу заметки на интересные темы. Даже чатик инвесторов у нас есть, присоединяйтесь
Корреляционный анализ – статистический инструмент, определяющий зависимость одного показателя от другого. В Excel есть функция определения этого коэффициента.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Источник: http://lumpics.ru/correlation-analysis-in-excel/
Синтаксис
КОРРЕЛ(массив1;массив2)
Аргументы функции КОРРЕЛ описаны ниже.
-
массив1 — обязательный аргумент. Диапазон значений ячеок.
-
массив2 — обязательный аргумент. Второй диапазон значений ячеев.
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB-995dcef7-0c0a-4bed-a3fb-239d7b68ca92
Что такое корреляция простыми словами
Не хочу вас сразу грузить формулами и расчётами, об этом поговорим ближе к концу. Давайте сначала разберемся, что по своей сути означает цифра коэффициента корреляции, которую вы можете встретить в какой-нибудь книге или статье.
Значение коэффициента может меняться от -1 до +1:
Если значение близко к единице или минус единице — значит два явления так или иначе сильно взаимосвязаны. Впрочем, причины этого не всегда очевидны — явление А может влиять на явление B, может быть наоборот. Нередко бывает, что существует явление C, которое приводит в движение А и В одновременно. В общем, природа корреляции — это уже второй вопрос, которым должны заниматься исследователи.
Околонулевые значения, в свою очередь, говорят об отсутствии какой-либо зависимости между явлениями. Нет конкретного предела, где заканчивается случайность и начинается взаимосвязь, все зависит от предмета исследования и количества данных. Навскидку, обычно при значениях от -0.3 до 0.3 можно говорить о том, что зависимость отсутствует.
При высокой положительной корреляции вслед за графиком А растёт и график B, и чем выше значение, тем слаженнее оба движутся. Для наглядности, вот как выглядит корреляция +1:
Движения графиков полностью повторяют друг друга, причем это как в случае простого добавления, так и с множителем.
При сильной отрицательной корреляции рост графика А приводит к падению графика B и наоборот. Вот так выглядит корреляция -1:
Движения графиков похожи на зеркальные отражения.
Коэффициент корреляции — удобный инструмент для анализа во многих сферах науки и жизни. Его легко рассчитать в Excel и применить, поэтому самая большая сложность в работе с ним — грамотно подобрать данные для расчёта. Основное правило — чем больше данных, тем лучше. Многие взаимосвязи проявляют себя лишь на длинной дистанции.
Также нужно следить за тем, чтобы найденные корреляции не были ложными.
↑ К СОДЕРЖАНИЮ ↑
Источник: http://webinvestor.pro/koeffitsient-korrelyatsii-v-excel-formula/
Ложные корреляции
Дело в том, что с помощью коэффициента корреляции можно проверить на взаимосвязь любые явления, которые можно выразить в числовом выражении. То есть, реально любые — например количество свадеб в Нью-Йорке и объем импорта нефти в США из Норвегии:

еще больше странных корреляций
Корреляция составила 86%! Действительно ли свадьбы влияют на экспорт нефти? Разумеется, нет — подобная зависимость совершенно случайна. Именно так выглядит ловушка ложной корреляции — она может показать взаимосвязь там, где её на самом деле нет.
Не хочу сильно заострять внимание на этой проблеме, так что если интересно поразбираться — нашел для вас видео, в котором найдете еще несколько примеров странных взаимосвязей и причины их появления:
В общем, на результаты корреляционного анализа есть смысл обращать внимание, когда связь между явлениями уже известна или подозревается. В противном случае это может быть всего лишь число, которое ничего не значит.
↑ К СОДЕРЖАНИЮ ↑
Источник: http://webinvestor.pro/koeffitsient-korrelyatsii-v-excel-formula/
Примеры использования
Рассмотрим несколько задач, чтобы понять принцип работы статистической функции.
Пример 1. В фирме есть бюджет на рекламную кампанию в месяц, а также есть объем продаж продукта, необходимо посчитать зависимость этих величин.
В произвольной ячейке записываете формулу со ссылкой на два диапазона и получаете число.
Результат близок к единице, значит между рекламой и продажами продукта существует сильная прямая зависимость.
Пример 2.
Есть показатели продаж мебели за квартал, а также изменение цены на товар за тот же период времени.
В данном случае коэффициент корреляции стремится к -1, что говорит о сильной обратной зависимости. То есть с увеличением цены товара, продажи падают.
Пример 3.
Имеются затраты на квартиру и еду за три месяца, необходимо вычислить зависимость этих статей расхода друг от друга.
Полученный результат говорит о слабой связи этих категорий.
Источник: http://mir-tehnologiy.ru/korrelyatsiya-v-excel/
Использование MS EXCEL для расчета ковариации
Ковариация близка по смыслу с дисперсией (также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а дисперсия – для одной. Поэтому, cov(x;x)=VAR(x).
Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() . В первом случае формула для вычисления аналогична вышеуказанной (окончание .Г обозначает Генеральная совокупность ), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание .В обозначает Выборка .
Примечание : Функция КОВАР() , которая присутствует в MS EXCEL более ранних версий, аналогична функции КОВАРИАЦИЯ.Г() .
Примечание : Функции КОРРЕЛ() и КОВАР() в английской версии представлены как CORREL и COVAR. Функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета ковариации :
= СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)
= СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)
= СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)
Эти формулы используют свойство ковариации :
Если переменные x и y независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А дисперсия их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
Источник: http://excel2.ru/articles/korrelyaciya-i-kovariaciya-v-ms-excel
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
В открывшемся окне перемещаемся в раздел «Параметры».
Далее переходим в пункт «Надстройки».
В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.


Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ
Источник: http://lumpics.ru/correlation-analysis-in-excel/
Пример
В следующем примере возвращается коэффициент корреляции двух наборов данных в столбцах A и B.
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB-995dcef7-0c0a-4bed-a3fb-239d7b68ca92
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
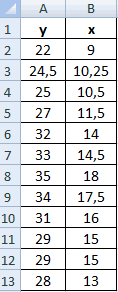
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
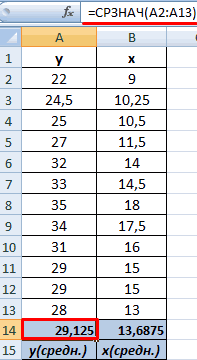
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
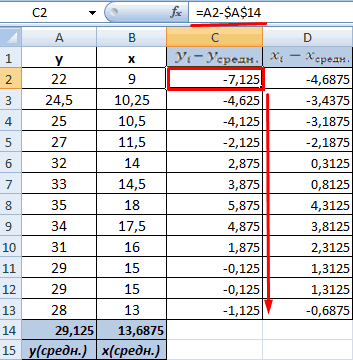
- Производим перемножение вычисленных разностей.
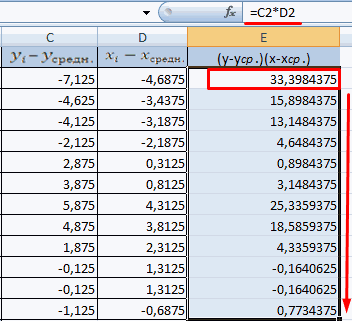
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
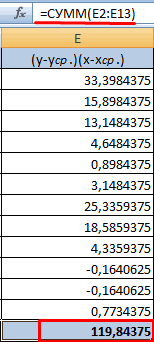
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
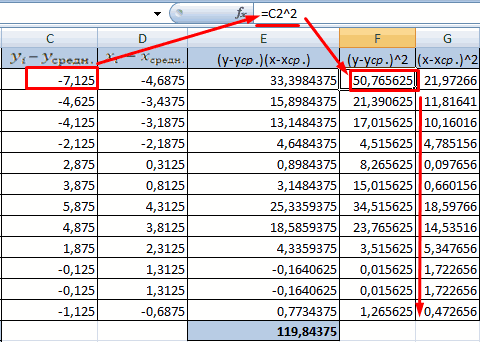
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
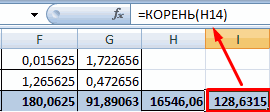
- Производим подсчет частного, используя значения знаменателя и числителя.
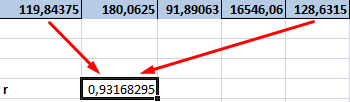
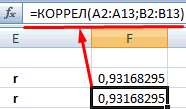
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
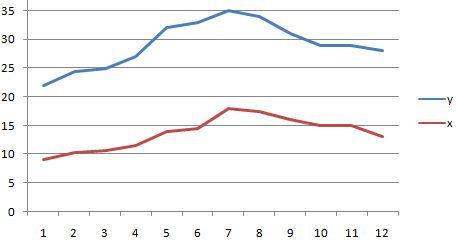
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
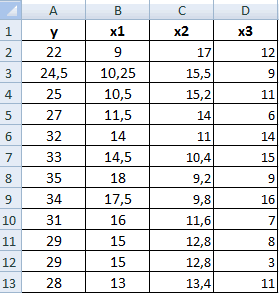
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
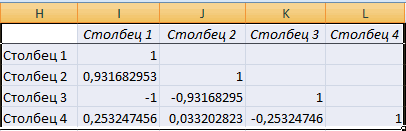
Источник: http://office-guru.ru/excel/korrelyacionnyj-analiz-v-excel-primer-vypolneniya-korrelyacionnogo-analiza.html
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» – «Диаграмма» – «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Источник: http://exceltable.com/otchety/korrelyacionno-regressionnyy-analiz
Коэффициент корреляции и ПАММ-счета
С расчётом корреляции я как студент экономического ВУЗа познакомился еще на втором курсе. Тем не менее, долгое время недооценивал важность расчёта корреляции именно для подбора ПАММ-портфеля. 2018 год очень четко показал, что ПАММ-счета с похожими стратегиями в случае кризиса могут вести себя очень похоже.
Случилось так, что с середины года отказала не просто одна стратегия управляющего, а большинство торговых систем, завязанных на активные движения валютной пары EUR/USD:
Рынок был для каждого управляющего по-своему неблагоприятным, но присутствие их всех в портфеле привело к большой просадке. Совпадение? Не совсем, ведь это были ПАММ-счета с похожими элементами в торговых стратегиях. Без опыта торговли на рынке Форекс может быть сложно понять, как это работает, но по корреляционной таблице степень взаимосвязи видна и так:
Мы ранее рассматривали корреляцию вплоть до +1, но как видите на практике даже совпадение в районе 20-30% уже говорит о некоторой схожести ПАММ-счетов и, как следствие, результатов торговли.
Чтобы снизить шансы на повторение ситуации, как в 2018 году, я считаю в портфель стоит подбирать ПАММ-счета с низкой взаимной корреляцией. По сути, нам нужны уникальные стратегии с разными подходами и разными валютными парами для торговли. На практике, конечно, сложнее подобрать прибыльные счета с уникальными стратегиями, но если хорошо покопаться в рейтинге ПАММ-счетов, то все возможно. К тому же, низкая взаимная корреляция снижает требования для диверсификации, 5-6 счетов вполне хватит.
Пару слов о расчёте коэффициента корреляции для ПАММ-счетов. Достать сами данные относительно несложно, в Альпари прямо с сайта, для остальных площадок через сайт investflow.ru. Однако с ними нужно сделать небольшие преобразования.
Данные о прибыльности ПАММов изначально хранятся в формате накопленной доходности, нам это не подходит. Корреляция стандартных графиков доходности двух прибыльных ПАММ-счетов всегда будет очень высокой, просто потому что они все движутся в правый верхний угол:
У всех счетов положительная корреляция от 0.5 и выше за редким исключением, так мы ничего не поймем. Реальное сходство стратегий ПАММ-счетов можно увидеть только по дневным доходностям. Рассчитать их не особо сложно, если знаете нужные формулы доходности. Если прибыль или убыток двух ПАММ-счетов совпадают по дням и по процентам, высока вероятность что их стратегии имеют общие элементы — и коэффициент корреляции нам это покажет:
Как видите, некоторые корреляции стали нулевыми, а некоторые остались на высоком уровне. Мы теперь видим, какие ПАММ-счета действительно похожи между собой, а какие не имеют ничего общего.
Напоследок давайте разберёмся, что делать и как посчитать корреляцию, если у вас появилась в этом необходимость.
↑ К СОДЕРЖАНИЮ ↑
Источник: http://webinvestor.pro/koeffitsient-korrelyatsii-v-excel-formula/
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB-995dcef7-0c0a-4bed-a3fb-239d7b68ca92
Коэффициент корреляции в Excel и формула расчёта
Вероятно, вас интересует, как самостоятельно рассчитать корреляцию двух инвестиционных активов. До изобретения компьютеров приходилось делать это вручную, для чего использовалась вот такая формула коэффициента корреляции:
- Rxy — коэффициент корреляции;
- COVxy — ковариация переменных X и Y;
- σX, σY — стандартное отклонение переменных X и Y
- X и Y с чертой — среднее значение Х и Y
Кстати, студентам на экзамене до сих пор компьютеров не выдают, хоть калькулятор можно и на том спасибо. Как вы понимаете, занятие все равно трудоёмкое 🙂
Профессиональному инвестору может понадобиться рассчитать сотни корреляций, так что вариант по формуле не подходит. Естественно, эта задача уже давно автоматизирована, и, как по мне, проще всего рассчитать коэффициент корреляции в Excel.
Чтобы далеко за примером не ходить, давайте рассчитаем корреляцию двух популярных ПАММ-счетов Lucky Pound и Hohla EUR. Они находятся на площадке компании Alpari, а значит мы можем скачать историю доходности прямо с сайта:
Далее нам надо скопировать историю доходности в один файл, для удобства. Для точного расчета корреляции в Excel нам в принципе хватит и двух лет истории, располагаем данные так:
Теперь, как я уже писал выше, для ПАММ-счетов (и для многих других инвестиционных инструментов) надо рассчитать дневные доходности:
А дальше все просто — используется встроенная формула коэффицента корреляции в Excel =КОРРЕЛ():
Получили значение 0.12, а значит стратегии ПАММ-счетов практически не имеют ничего общего. Это хорошо для диверсификации, так что можно добавлять обоих в инвестиционный портфель.
При желании, можно сделать табличку на весь ваш портфель. Тогда если у вас появится новый вариант для инвестирования, вы сможете сразу сравнить его с каждым активом и увидеть, есть ли нежелательные корреляции.
↑ К СОДЕРЖАНИЮ ↑
Мне понравилось работать над этой темой и статья получилась неплохой. Есть еще одна интересная тема по основам инвестирования, которую я хочу подробно обсудить… Будет обидно, если пропустите, так что подписывайтесь на обновления блога по почте или через соцсети.
До встречи и успешных вам инвестиций!

(
Telegram
,
VK
,
). Уже несколько лет веду блог об инвестировании в Интернете и делюсь реальными результатами своего
публичного портфеля
. В свободное время делаю в Microsoft Excel вспомогательные инструменты для инвесторов. Также изучаю SEO и методы монетизации сайтов, используя блог как полигон для экспериментов.
Источник: http://webinvestor.pro/koeffitsient-korrelyatsii-v-excel-formula/
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
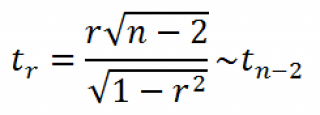
Источник: http://office-guru.ru/excel/korrelyacionnyj-analiz-v-excel-primer-vypolneniya-korrelyacionnogo-analiza.html
Правила отбора факторов корреляционного анализа
При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.
Источник: http://brit03.ru/programmy/korrelyacionnyj-analiz-v-excel.html
Пример применения метода корреляционного анализа
В Великобритании было предпринято любопытное исследование. Оно посвящено связи курения с раком легких, и проводилось путем корреляционного анализа. Это наблюдение представлено ниже.
Исходные данные для корреляционного анализа
| Профессиональная группа | смертность |
| Фермеры, лесники и рыбаки | |
| Шахтеры и работники карьеров | |
| Производители газа, кокса и химических веществ | |
| Изготовители стекла и керамики | |
| Работники печей, кузнечных, литейных и прокатных станов | |
| Работники электротехники и электроники | |
| Инженерные и смежные профессии | |
| Деревообрабатывающие производства | |
| Кожевенники | |
| Текстильные рабочие | |
| Изготовители рабочей одежды | |
| Работники пищевой, питьевой и табачной промышленности | |
| Производители бумаги и печати | |
| Производители других продуктов | |
| Строители | |
| Художники и декораторы | |
| Водители стационарных двигателей, кранов и т. д. | |
| Рабочие, не включенные в другие места | |
| Работники транспорта и связи | |
| Складские рабочие, кладовщики, упаковщики и работники разливочных машин | |
| Канцелярские работники | |
| Продавцы | |
| Работники службы спорта и отдыха | |
| Администраторы и менеджеры | |
| Профессионалы, технические работники и художники |
Начинаем корреляционный анализ. Решение лучше начинать для наглядности с графического метода, для чего построим диаграмму рассеивания (разброса).
Она демонстрирует прямую связь. Однако на основании только графического метода сделать однозначный вывод сложно. Поэтому продолжим выполнять корреляционный анализ. Пример расчета коэффициента корреляции представлен ниже.
С помощью программных средств (на примере MS Excel будет описано далее) определяем коэффициент корреляции, который составляет 0,716, что означает сильную связь между исследуемыми параметрами. Определим статистическую достоверность полученного значения по соответствующей таблице, для чего нам нужно вычесть из 25 пар значений 2, в результате чего получим 23 и по этой строке в таблице найдем r критическое для p=0,01 (поскольку это медицинские данные, здесь используется более строгая зависимость, в остальных случаях достаточно p=0,05), которое составляет 0,51 для данного корреляционного анализа. Пример продемонстрировал, что r расчетное больше r критического, значение коэффициента корреляции считается статистически достоверным.
Источник: http://brit03.ru/programmy/korrelyacionnyj-analiz-v-excel.html
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» – первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» – второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
- Строим корреляционное поле: «Вставка» – «Диаграмма» – «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Проведение корреляционного анализа средствами MS Excel .
Построим матрицу коэффициентов парной корреляции.
Выбираем команду меню Сервис/Анализ данных/Корреляция. Откроется следующее диалоговое окно:
Далее следует нажать кнопку OK. После этого будет создана матрица коэффициентов парной корреляции:
| Х1 | Х3 | Х6 | Х8 | Х9 | У |
| Х1 | |||||
| Х3 | 0,594 | ||||
| Х6 | 0,708 | 0,51 | |||
| Х8 | 0,542 | 0,302 | 0,633 | ||
| Х9 | -0,63 | -0,63 | -0,75 | -0,68 | |
| У | -0,55 | -0,35 | -0,87 | -0,62 | 0,719 |
| Х1 | Х3 | Х6 | Х8 | Х9 | У |
| Х1 | |||||
| Х3 | 0,594 | ||||
| Х6 | 0,708 | 0,51 | |||
| Х8 | 0,542 | 0,302 | 0,633 | ||
| Х9 | -0,63 | -0,63 | -0,75 | -0,68 | |
| У | -0,55 | -0,35 | -0,87 | -0,62 | 0,719 |
Анализ матрицы коэффициентов парной корреляции показывает, что наиболее существенное влияние на зависимую переменную оказывают все факторы Х6,Х8,Х9 (см. строку Y).
X9 сильно связана с х6 (из них надо оставить одну, например, х6),
Для исключения явления мультиколлинеарности все факторы кроме X6 и X8 следует исключить из модели.
· Построить уравнение множественной линейной регрессии, используя надстройку MS Excel Пакет анализа (команда Сервис Анализ данных Регрессия)
Ищем линейное уравнение множественной регрессии в виде:
Параметры данного уравнения найдем с помощью инструмента «Регрессия» надстройки «Анализ данных» приложения MS Excel (результаты вычисления – в Приложении 7):
Для построения линейной регрессионной модели вMS Excel необходимо:
1) подготовить список из n строк и m столбцов, содержащий экспериментальные данные (столбец, содержащий выходную величину y должен быть либо первым, либо последним в списке);
2) обратиться к меню Сервис/Анализ данных/Регрессия
Если пункт “Анализ данных” в меню “Сервис” отсутствует, то следует обратиться к пункту “Надстройки” того же меню и установить флажок “Пакет анализа”.
3) в диалоговом окне “Регрессия” задать:
- входной интервал Y;
- входной интервал X;
- выходной интервал – верхняя левая ячейка интервала, в который будут помещаться результаты вычислений (разместим на том же рабочем листе);
Настройки для решения поставленной задачи показаны на рисунке окна “Регрессия”.
· нажать “Ok” и проанализировать результаты.
Результаты расчетов размещены в 4-x таблицах
Коэффициенты регрессии находятся в таблице «Дисперсионный анализ» в столбце «Коэффициенты»
Получаем уравнение линейной множественной регрессии:
В регрессионном анализе наиболее важными результатами являются:
- коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели;
- множественный R, характеризующий точность модели для имеющихся исходных данных;
- F-критерий Фишера (в рассмотренном примере он значительно превосходит критическое значение, равное 4,06);
t-статистика– величины, характеризующие степень значимости отдельных коэффициентов модели
3) Определить значения коэффициента множественной корреляции и коэффициента детерминации и сделать выводы об адекватности построенной модели.
Величина множественного коэффициента детерминации R 2 =0,763361 рассчитана в таблице “Регрессионная статистика”
| Регрессионная статистика | |
| Множественный R | 0,873706 |
| R-квадрат | 0,763361 |
| Нормированный R-квадрат | 0,743642 |
| Стандартная ошибка | 8,931274 |
| Наблюдения |
| значения коэффициента множественной корреляции | 0,873706 | Теснота совместного влияния факторов на результат довольна высокая (больше, чем 0,7) |
| значения коэффициента детерминации | 0,763361 | Больше чем 0,5. Модель объясняет более 76% дисперсии зависимой переменной. |
Построенную модель на основе этого параметра можно признать достаточно качественной. А изменение результативного показателя примерно на 76 % обусловлено влиянием факторов, включенных в модель.
Задачей построения регрессионной зависимости является нахождение вектора коэффициентов M модели (1) при котором коэффициент R принимает максимальное значение.
Значимость R определяется не только его величиной, но и соотношением между количеством экспериментов и количеством коэффициентов (параметров) модели. Действительно, корреляционное отношение для n=2 для простой линейной модели равно 1 (через 2 точки на плоскости можно всегда провести единственную прямую). Однако, если экспериментальные данные являются случайными величинами, доверять такому значению R следует с большой осторожностью. Обычно для получения значимого R и достоверной регрессии стремятся к тому, чтобы количество экспериментов существенно превышало количество коэффициентов модели (n>>k).
4) Оценить значимость уравнения регрессии в целом (при заданном уровне значимости) (с помощью F-критерия Фишера) (статистическую надежность моделирования)
Корреляционный анализ в системе STATISTICA 6.1
Порядок входа Анализ —> Основные статистики и таблицы —> Парные и частные корреляции —>ОК [3,4, 14].
Перед нами рабочие окна всех действий (рис. 7.1, 7.2).
Рис. 7.1. Стартовая панель модуля Основные статистики и таблицы
Рис. 7.2. Рабочие окна ввода параметров для расчета Парных и частных корреляций
Вводим исходные данные, нажимаем клавишу Квадратная матрица и в появившемся окне, в строке Первый список, вводим исходные данные (рис. 7.3).
Для отображения решения выбираем вкладку Опции и нажимаем окошечко Матрица парных корреляций. Получаем решение (рис. 7.4).
Рис. 7.3. Вкладка Парные и частные корреляции
Рис. 7.4. Решение матрицы парных корреляций
Можно вывести подробную информацию, если на вкладке Парные и частные корреляции (рис. 7.5) выбрать Опции и отметить Подробная таблица результатов —? ОК вместо таблицы (рис. 7.4) появится таблица (рис. 7.6).
Детализированная матрица для каждой пары переменных включает среднее значение, стандартное отклонение, коэффициенты корреляции Пирсона и детерминации, ^-критерий Стьюдента для сравнения средних двух выборок (переменных в данном случае), уровень значимости, объем выборки, коэффициенты линейных уравнений регрессии.
Значимая корреляционная связь выделена красным цветом.
Результаты аналогичны табл. 7.3, выполненным вручную.
Все рассуждения аналогичны приведенным в п. 7.2, 7.3.
Система STATISTICA позволяет построить как дополнительные таблицы, так и графики, которые помогают более детально провести корреляционный анализ.
Рис. 7.5. Выбор опции «Подробная таблица результатов»
Рис. 7.6. Подробная таблица результатов корреляции
Например, в окне Парные и частные корреляции (рис. 7.3) вывести Матрицу (рис. 7.7), которая содержит, парные коэффициенты корреляциии и статистику по каждой из переменных, или построить матрицу диаграмм рассеивания для всех переменных (рис. 7.8). Диаграммы более наглядно, чем таблицы, демонстрируют взаимосвязи между переменными.
Есть возможность вывести диаграмму рассеивания для каждого случая в отдельности с нанесенными доверительными интервалами. На рис. 7.9 показана диаграмма рассеивания для переменных Ни А.
Если есть необходимость, можно вывести диаграмму ЗН-рассеивания (рис. 7.10,7.11).
Рис. 7.7. Таблица данных матрицы парных корреляции
Рис. 7.8. Матрица диаграмм рассеивания для всех переменных
Корреляция между двумя переменными, вычисленная при фиксированных уровнях всех других, называется частной корреляцией. Ниже приведены эти вычисления.
Рис. 7.9. Диаграмма рассеивания для частного случая
Рис. 7.10. Рабочие окна для ввода данных при построении диаграммы ЗР-рассеивания (окончание см. на с. 186)
Рис. 7.10. Окончание (начало см. на с. 185)
Рис. 7.11. Диаграмма Зй-рассеивания
Выбираем частные корреляции и вводим переменные.
- 1. Исключаем влажность W, получим рис. 7.12 (ввод исходных данных) и рис. 7.13 (частные корреляции).
- 2. Исключаем высоту откоса Я, получим рис. 7.14.
- 3. Исключаем А, получим рис. 7.15.
4. Исключаем угол внутреннего трения R, получаем рис. 7.16. Красным цветом отмечены значимые коэффициенты корреляции для принятого уровня значимости р = 0,05.
Рис. 7.12. Далоговое окно ввода исходных данных для расчета частной корреляции
Рис. 7.13. Таблица результатов расчета частных корреляций при исключенной влажности
Рис. 7.14. Таблица результатов расчета частных корреляций при исключении высоты откоса
Рис. 7.15. Таблица результатов расчета частных корреляций при исключении угла откоса
Рис. 7.16. Таблица результатов расчета частных корреляций при исключении угла внутреннего трения
Значения коэффициентов корреляции второго порядка, приведенные в табл. 7.13-7.16 (вычисляемые по формуле (7.8)) определяют частные коэффициенты корреляции первого порядка, аналогичные приведенным в табл. 7.4-7.7.
Исключение только парных коэффициентов корреляции уже существенно изменило картину, например, из табл. 7.4 видно, что
т. е. частные коэффициенты стали значительно больше, чем те же парные коэффициенты корреляции,
т. е. связь уже обозначалась как сильная, т. е. закрепление одного из элементов увеличило связь между Я и аиЯир.
Продолжим наши исследования и найдем коэффициенты корреляции второго порядка, которые определялись по формуле (7.9). Результаты расчета были представлены в табл. 7.8.
Результаты для двух сочетаний представлены на рис. 7.17, 7.18.
Рис. 7.17. Результаты сочетаний высоты и угла откоса
Рис. 7.18. Результаты сочетаний угла откоса и угла внутреннего трения
Пример из табл. 7.8 совпадает с расчетом, показанным на рис. 7.18. Анализ аналогичен приведенному в п. 7.3.
Корреляция и ковариация в Microsoft Excel
Microsoft Excel имеет значительно меньшие возможности, нежели система STATISTICA.
Вызыв функций Ковариация и Корреляция осуществляется как обычно: Данные —? Анализ данных —? Ковариация (Корреляция) —?ОК (рис. 7.19).
Работа функции Ковариация представлена на рис. 7.20, а функции Корреляция – на рис. 7.21.
Рис. 7.19. Стартовая панель для вызова функций Ковариация и Корреляция
Рис. 7.20. Работа функции ковариация
Рис. 7.21. Работа функции корреляция
Значения корреляционных коэффициентов аналогичны вычисленным вручную и в системе STATISTICA.
Корреляционный анализ в EXCEL
Практическое занятие «Проверка адекватности модели».
Цель работы: Изучение t-критерия Стьюдента.
Чтобы определить насколько полученное уравнение регрессии значимо для всей совокупности, необходимо проверить:
• Определение значимости модели
• Установление наличия или отсутствия систематической ошибки.
Проверка значимости отдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы о равенстве нулю каждого коэффициента регрессии.
Расчетные значения t -критерия сравнивают с табличным значением критерия, которое определяется при (n-k-1) степенях свободы и соответствующем уровне значимости α.
n – число уравнений,
k – число переменных,
α = 0,05 при доверительной вероятности 0,95 .
Формула для определения t-критерия Стьюдента:
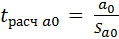
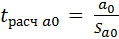
где Sa0 и Sa1 – стандартные отклонения свободного члена и коэффициента регрессии.
Определяются по формулам:




Задание: Рассчитать t-критерий Стьюдента по данным в табл.3 и сделать выводы о значимости отдельных коэффициентов уравнения регрессии.
0,636263125
a0=
-109
ε 2
( xi – хср. ) 2
1
3357
2425
2027
2
3135
2050
1886
3
2842
1683
1700
4
3991
2375
2431
5
2293
1167
1350
6
3340
1925
2017
7
3089
1042
1857
8
4372
2925
2673
9
3563
2200
2158
10
3219
1892
1940
11
3308
2008
1996
12
3724
2225
2261
13
3416
1983
2065
14
3022
2342
1814
15
3383
2458
2044
16
4267
2125
2606
Сумма
Расчет t-критерий Стьюдента можно также произвести с помощью Excel, используя стандартную функцию, приведенную в таблице 4.
Сервис / Анализ данных
Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия
| Оценка параметров модели парной и множественной линейной регрессии. | |
Оценка значимости коэффициента парной корреляции с использованием t – критерия Стьюдента.  Вычисленное по этой формуле значение tнабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2). Вычисленное по этой формуле значение tнабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2). |
СТЬЮДРАСПОБР (вероятность; степени_свободы) Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы — число степеней свободы, характеризующее распределение. |
Сделать выводы о значимости коэффициентов уравнения регрессии.
Практическое занятие «Определение значимости модели по F – критерию Фишера»
Цель работы: Изучение F- критерия Фишера.
Для проверки значимости уравнения регрессии в целом используется F – критерий Фишера.
В случае парной линейной регрессии критерий определяется:


Если при заданном уровне значимости расчетное значение F – критерий Фишера с γ 1= k , γ 2 = n – k -1 степенями свободы больше табличного, то модель считается значимой
Задание: Используя данные предыдущей работы, рассчитать F- критерий Фишера и сделать выводы.
Для расчета следует воспользоваться инструментом Регрессия из пакета Сервис / Анализ данных и выбрать значение.
Расчет F-критерий Фишера можно также произвести с помощью Excel, используя стандартную функцию (см. табл.5)
Оценка параметров модели парной и множественной линейной регрессии.
Для вычисления параметров уравнения регрессии следует воспользоваться инструментом РегрессияПроверка значимости модели регрессии с использованием F-критерий Фишера 
Дата добавления: 2019-07-15 ; просмотров: 110 ;