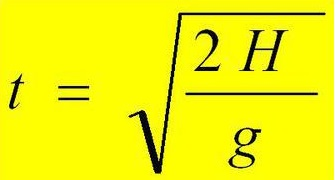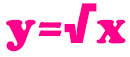Корень отрезка в excel - Word и Excel - помощь в работе с программами

Как в офисе.

Рассмотрим пример нахождения всех корней уравнения

Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно надо локализовать. С этой целью необходимо полином протабулировать. Построим таблицу значений полинома на отрезке [—1,1] с шагом 0,2 и график полинома. Результат приведен на рис. 29, где в ячейку В2 введена формула

=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.

На рис. 29 видно, что полином меняет знак на интервалах [—1,—0,8], [0,2, 0,4] и [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, мы локализовали все его корни.

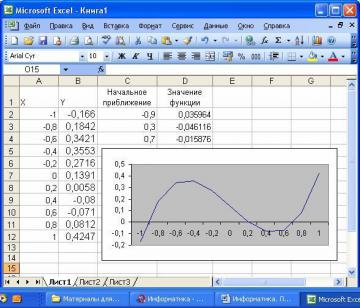
Найдем корни полинома методом последовательных приближений с помощью команды Сервис / Подбор параметров. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис / Параметры (рис. 30).

Зададим относительную погрешность и предельное число итераций равными 0,00001 и 1000 соответственно. В качестве начальных приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем в качестве начальных приближений их средние точки: —0.9, 0.3, 0,7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу

=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.

Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. В ячейках D2:D4 будут вычислены значения полинома при значениях аргумента, введенных в ячейки C2:C4.

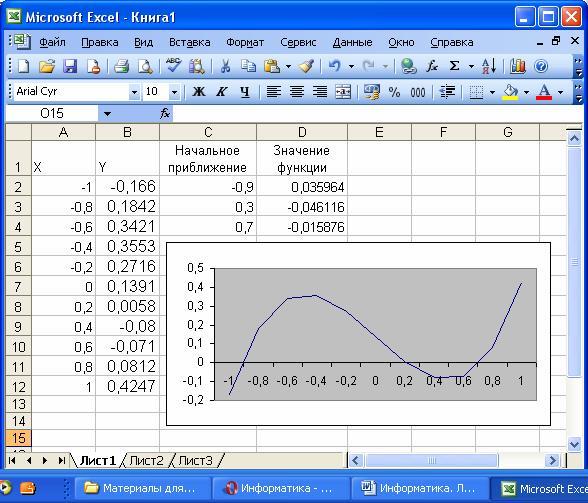
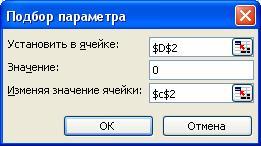
Теперь выберем команду Сервис / Подбор параметров и заполним диалоговое окно Подбор параметров следующим образом (рис. 31).

В поле Установить в ячейке введем D2. В этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. В поле Значение введем 0 (в этом поле указывается правая часть уравнения). В поле Изменяя значение ячейки введем С2 (в этом поле дается ссылка на ячейку, отведенную под переменную).

Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки (в нашем примере в $D$2 и $C$2).

После нажатия кнопки ОК средство подбора параметров находит приближенное значение корня, которое помещается в ячейку С2. В данном случае оно равно —0,920. Аналогично в ячейках С3 и С4 находим два оставшихся корня. Они равны 0,210 и 0,720.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Кафедра прикладной математики и вычислительной техники

Решение нелинейных уравнений в Excel и Mathcad

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.

Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика».

Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования.

Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.

Рецензент к. ф-м. н.

Ó , составление, 2012

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.6 Метод Ньютона (касательных)

1.7 Комбинированный метод

1.8 Метод итераций

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

3 Задания к лабораторным работам

Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения

Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения

Лабораторная № 3. Решение систем нелинейных уравнений

Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем

4 Вопросы и тесты для самоконтроля

Список рекомендуемой литературы

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн.

В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью.

Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс).

1.2 Отделение корней

Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0.

Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной.

Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения».

Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения.

На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню.

Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.

Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения

1.3 Уточнение корней стандартными средствами Excel и Mathcad

Во всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка.

В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.

Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel

Рисунок 3 – Результаты использования средств решения уравнения в Excel

В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.

Рисунок 4 – Решение уравнения с использованием функции root(…) в Mathcad

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad

Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно.

В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет».

Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции).

1.4 Метод деления отрезка пополам

В этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге.

Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001.

Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы.

На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: ВставкаФункцияЛогические). Для нового левого края отрезка мы проверяем истинность условия f(a)*f(c)>0, если оно верно, то мы в качестве нового значения левого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [a, c] нет), иначе оставляем значение a. Аналогично, для нового правого края отрезка мы проверяем истинность условия f(c)*f(b)>0, если оно верно, то мы в качестве нового значения правого конца отрезка берем число c (т. к. это условие показывает, что корня на отрезке [c, b] нет), иначе оставляем значение b.

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.

Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться.

Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].

Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel

Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad

1.5 Метод хорд

В этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:

1.6 Метод Ньютона (касательных)

Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:

Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня.

Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях.

Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции.

Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.

Точность вычислений можно оценить из соотношения

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:

где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.

Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.

Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно.

Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0.

Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя).

2.2 Решение систем нелинейных уравнений методом Ньютона

Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:

Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).

Для расчета новых приближений на шаге i+1 используется матричная формула

Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных.

Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям.

В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула

Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad.

2.3 Решение систем нелинейных уравнений методами итераций

Для реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид

Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:

Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений:

источники:

http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/

http://pandia.ru/text/78/157/38912.php

Источник

Лабораторная работа

Отделение корней
нелинейного уравнения

Пусть имеется
нелинейное уравнение .

Требуется найти
корни этого уравнения. Численный процесс приближенного решения поставленной
задачи разделяют два этапа: отделение корня и уточнение корня.

Для отделения
корня необходимо определить промежуток аргумента , где
содержится один и только один корень уравнения. Одна из точек этого промежутка
принимается за начальное приближение корня. В зависимости от метода, который
предполагается использовать для уточнения корня, требуется определение
некоторых свойств отделенного корня и поведения функции на отрезке отделения.
Например, при использовании метода деления пополам, необходимо и достаточно
установить лишь непрерывность функции на отрезке отделения.

Этап отделения
корня уравнения алгоритмизирован только для некоторых классов уравнений
(наиболее известным из которых является класс алгебраических уравнений),
поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с
использованием всей возможной информации о функции . Часто
применяется графический метод отделения действительных корней, обладающий
большой наглядностью.

Методы
отделения корней

Отделение корней
во многих случая можно произвести графически. Учитывая, что действительные
корни уравнения F(x)=0 – это есть точки пересечения графика
функции y=F(x) с осью абсцисс y=0, нужно построить
график функции y=F(x) и на оси OX отметить отрезки,
содержащие по одному корню. Но часто для упрощения построения графика функции y=F(x)
исходное уравнение заменяют равносильным ему уравнением f₁(x)=f₂(x).
Далее строятся графики функций y₁=f₁(x)
и y₂=f₂(x), а затем по оси OX
отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.

На практике
данный способ реализуется следующим образом: например, требуется отделить корни
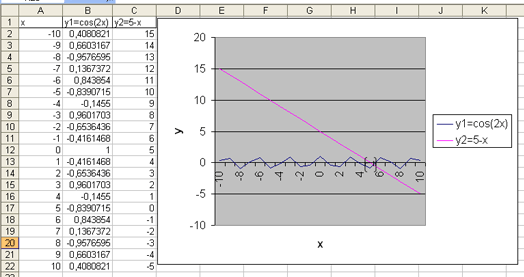
уравнения cos(2x)+x-5=0 графически на отрезке [–10;10],
используя Excel.

1 способ

Построим график функции f(x)=cos(2x)+x-5
в декартовой системе координат. Для этого нужно:

1.
Ввести в
ячейку A1 текст х.

2.
Ввести в
ячейку B1 текст y=cos(2x)+x-5.

3.
Ввести в
ячейку А2 число -10, а в ячейку А3 число -9.

4.
Выделить
ячейки А2 и А3.

5.
Навести
указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий
выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы
рамка охватила диапазон ячеек А2:А22.

6.
Ячейки
автоматически заполняются цифрами :

7.
Ввести в
ячейку В2 формулу =COS(2*A2)+A2-5.

8.
Методом
протягивания заполнить диапазон ячеек В3:В22.

9.
Вызвать
«Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать
«далее».

10.
Указать
диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон
данных В2:В22.

11.
Выбрать
вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.

12.
В поле
«подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».

13.
Подписать
названия осей x и y соответственно, нажать «далее».

14.
Вывести
диаграмму на том же листе, что и таблица, нажать кнопку «готово».

В итоге получаем следующее
(рисунок 1):

Рисунок 1 – Локализация корня

Анализируя полученное
изображение графика, можно сказать, что уравнение cos(2x)+x-5=0
имеет один корень – это видно из пересечения графика функции y=cos(2x)+x-5
с осью OX. Можно выбрать отрезок, содержащий данный корень:[5;6] – отрезок локализации.

2 способ

Для подтверждения полученных
данных, можно решить эту же задачу вторым способом. Для этого необходимо
уравнение cos(2x)+x-5=0 преобразовать к виду: cos(2x)=5-x.
Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y₁=cos(2x)
и y₂=5-x. Для решения этой задачи в Excel необходимо
выполнить следующие действия:

1.
Вести в
ячейки А1:C1 соответственно текст: «x», «y₁=cos(2_x)»,
«y₂=5-x».

2.
A2:A22
заполнить так же как при решении задачи первым способом.

3.
В В2
ввести формулу =COS(2*A2).

4.
Методом
протягивания заполнить диапазон ячеек В3:В22.

5.
В С2
ввести =5-A2.

6.
Методом
протягивания заполнить диапазон ячеек С3:С22.

7.
С помощью
Мастера диаграмм выбрать график (первый вид).

8.
В данном
случае диапазон данных следует указывать для построения двух графиков. Для
этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем
нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.

9.
Перейти
на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.

10.
Подписать
ось x , выбрав диапазон А2:А22.

11.
Подписать
соответственно оси x и y.

12.
Поместить
диаграмму на имеющемся листе.

Результат представлен на
рисунке 2: Анализируя
полученный результат, можно сказать, что точка пересечения двух графиков
попадает на тот же самый отрезок локализации [5;6], что и при решении задачи
первым способом.

Рисунок 2 – Локализация корня

Аналитический способ отделения
корней

Аналитический
способ отделения корней основан на следующей теореме, известной из курса математического
анализа.

ТЕОРЕМА: Если непрерывная на функция ,
определяющая уравнение , на концах отрезка принимает значения разных знаков, т.е. , то на этом отрезке содержится, по
крайней мере, один корень уравнения. Если же функция непрерывна
и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один
корень уравнения.

В случае, когда
на концах интервала функция имеет одинаковые знаки, на этом интервале корни
либо отсутствуют, либо их четное число.

Для отделения корней
аналитическим способом выбирается отрезок , на
котором находятся все интересующие вычислителя корни уравнения. Причем на
отрезке функция F(x) определена, непрерывна и F(a)*F(b)<0.
Требуется указать все частичные отрезки ,
содержащие по одному корню.

Будем вычислять
значение функции F(x),
начиная с точки x=a, двигаясь вправо с некоторым шагом h. Если F(x)*F(x+h)<0,
то на отрезке [x;x+h] существует корень (рисунок 3).

Рисунок 3 –
Аналитический способ локализации корней

Если F(x_k)=0,
x_k-точный корень.

Доказательство существования
и единственности корня на отрезке.

В качестве примера рассмотрим
функцию f(x)=cos(2x)+x-5.

1. Ввести в ячейки А1, В1 и С1
соответственно «x», «y=cos(2x)+x-5» и «ответ».

2. В А2 и А3 ввести граничные
значения отрезка изоляции.

3. В В2 ввести формулу
=COS(2*A2)+A2-5 и методом протягивания заполнить В3.

4. В С2 ввести формулу
=ЕСЛИ(B2*B3<0;»корень существует»;»корень не
существует»).

Таким образом, на отрезке
изоляции корень существует:

Рисунок 4 – Проверка существования корня на отрезке

Для доказательства
единственности корня на отрезке изоляции необходимо выполнить следующие
действия:

1.
Продолжить
работу в том же документе MS Excel.

2.
Заполнить
D1 и E1 соответственно: «y’=-sin(2x)*2+1» и «ответ» (причем выражение
y’=-sin(2x)*2+1 – это производная первого порядка от функции y=cos(2x)+x-5).

3.
Ввести в
D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

4.
Ввести в
E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень
не единственный»).

В результате получаем
(рисунок 5):

Рисунок 5 –
Доказательство единственности корня на отрезке

Таким образом доказано
существование и единственность корня на отрезке изоляции.

Рассмотрим
решение задачи отделения корней уравнения
cos(2x)+x-5=0 аналитическим
способом с шагом 1 на отрезке [-10;10].

Чтобы отделить корни
уравнения аналитическим способом с помощью Excel, необходимо выполнить
следующее:

1.
Заполнить
ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5»,
«h», «ответ».

2.
В С2
ввести значение 1.

3.
Ввести в
А2 значение -10.

4.
Ввести в
А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

5.
В В2
ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

В С3 ввести формулу
=ЕСЛИ(B2*B3<0;»Корень на отрезке существует»;ЕСЛИ(B3=0;»точный
корень»;»-«)) и методом протягивания заполнить диапазон ячеек
С4:С22.

В результате получаем
следующее (рисунок 6):

Рисунок 6 –
Отделение корня

Следующий пример (рисунок
7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos(x)=0,1x на интервале [–10;10] с шагом
1.

Табулирование
функции и построение графика осуществляется как в предыдущих примерах. Видно,
что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9];
[-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].

Рисунок 7 – Отделение корней

Обратим внимание
на то, что надежность рассмотренного алгоритма отделения корней уравнения
зависит как от характера функции F(x), так и от выбранной величины шага h.
Для повышения надежности следует выбирать при отделении корней достаточно малые
значения h.

Задание

1. Выполнить отделение корней
следующих функций:

№ п/п	Уравнение	A	B
1	tg(x) = 1/x	0	n/2
2	e ^-x = x	0	1
3	ln(x) = 1/x	1	2
4	2 +ln(x) = 1/x	0	1
5	x — x³ + 1 =0	1	2

2. Выполнить индивидуальные задания

Вариант 1

1	ctg(x) = —x²	1,6	4,5
2	2ln(x)+sin(x) =e ^x	0	2
3	lg(x) = 2 ^x-x³	0	10
4	cos(x) = 1/x	0	p/2
5	cos(x) = ln(1+x)	0	p/2

Вариант 2

1	tg(x) = 1/x—x²	1,6	4,5
2	2ln(x) =e ^x	0	2
3	lg(x) = sin(x)	0	10
4	cos(x)+x² = 1/x	0	p/2
5	cos²(x) = ln(1+x²)	0	p/2

Вариант 3

1	cos²(x) = x	p/2
2	1 — 3 x + x3=0	1
3	1 — 3x + x4=0	1
4	1 — 3 x + x⁵=0	1
5	tg(x) = 1/x2	p/2

Вариант 4

1	ln(x) = sin(x)	1	3
2	e ^— ^x = sin(x)	0	p/2
3	e ^x = 1 /sin(x)	0	p/2
4	e ^— ^x = x²	0	1
5	2 + ln(x) = 1/x²	0	1

Вариант 5

1	ln(x) = Sin (x)	0	p/2
2	x — x³ + 2 =0	1	2
3	x +5 = x³	1	2
4	x ²— 0,5 x-2=0	0	0,5
5	ln(x -1)+ x-2=0	1	3

Вариант 6

1	ln(x+3) = Sin (x)	0	p/2
2	2x — x³ + 3 =0	1	2
3	x +8 = x³+x²	1	2
4	x — 0,5 x²+4=0	0	0,5
5	(x -1)²— x=0	1	3

Вариант 7

1	x +0,5 = e ^-x	0	1
2	2 — x + x³=0	-2	0
3	sin(x) = 1/x	0	p/2
4	sin(x) = x/2	п/2	п
5	ln(x) = e ^-x	0	2

Вариант 8

1	lg(x) = e ^— ^x	1
2	cos(x) = x	p/2
3	cos(x) = ln(x)	p/2
4	cos(x) = tg(x)	p/2
5	cos(x) = x³	p/2

Вариант 9

1	1 — 5 x + x³=0	0	1
2	1 — 5 x + x⁴=0	0	1
3	1 — 3 x + x⁵=0	1	2
4	4cos(x) = x+x²	0	p/2
5	cos(x) = ln(x)-x²	0	p/2

Вариант 10

1	ln(x) = cos (x)	0	p/2
2	x² — x³ + 2 =0	1	2
3	cosx +5 = x³	1	2
4	x ^0,5— x=0	0	0,5
5	(x -1)²— x=5	1	3

Вариант 11

1	ln(x+3) =sin (x)-x	0	p/2
2	2x — x³ + 3 =ln(x)	1	2
3	cos(x) +2 = x³+x²	1	2
4	3x — 0,5 x²+cosx=0	0	0,5
5	(x -1)²— x+tg(x-1)=0	1	3

Вариант 12

1	x² +0,5 = e ^-x	0	1
2	2 – sin(x) + x³=0	-2	0
3	sin(x) = 1/x-x²	0	p/2
4	sin(x) = x/2+cos(x)	п/2	п
5	ln(x)-x = e ^-x	0	2

Вариант 13

1	lg(x)+2sin²(x) = e ^— ^x	1
2	cos(x+p/2) = x+x²	p/2
3	cos(x) = ln(x)-x²	p/2
4	cos(x) = tg(x)+sin(2x-p/2)	p/2
5	cos(x) = x³-log(x²)	p/2

Вариант 14

1	1 — 5 cos(x) + x³=0	0	1
2	1 — 5 tg(x) + x⁴=0	0	1
3	1 – 3( x-2)² + x⁵=0	1	2
4	4cos(x) = cos(x)+x²	0	p/2
5	cos(x) = ln(x)-x²+x	0	p/2

Источник

Функция КОРЕНЬ принадлежит к категории Математических функций в Excel и возвращает положительное значение квадратного корня из числа.

Примеры использования функции КОРЕНЬ для математических расчетов в Excel

Пример 1. С помощью секундомера и небольшого предмета (например, камня), можно определить высоту здания (отпустить камень в свободное падение и засечь на секундомере моменты между началом движения и соприкосновения с поверхностью земли). Однако, зная высоту, можно рассчитать время, которое потребуется предмету на свободное падение. Для этого можно использовать следующую формулу: t=√(2H/g).

Где:

t – искомая величина времени падения;
H – высота, с которой предмет запущен в свободное падения;
g – ускорение свободного падения (пример равным 9,81).

Рассчитаем, сколько будет падать предмет с высоты 200 м (сопротивлением воздуха пренебрежем).

Внесем исходные данные в таблицу:

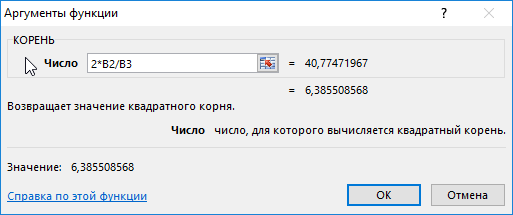
Для расчета используем следующую формулу:

=КОРЕНЬ(2*B2/B3)

В качестве параметра функция принимает выражение 2*B2/B3, где:

B2 – ячейка с данными о высоте, с которой запущен предмет;
B3 – ячейка, содержащая данные об ускорении свободного падения.

В результате получим:

То есть, время падения составит примерно 6,4 с.

Как построить график функции в Excel?

Пример 2. Функцию КОРЕНЬ удобно использовать для построения графика следующего типа:

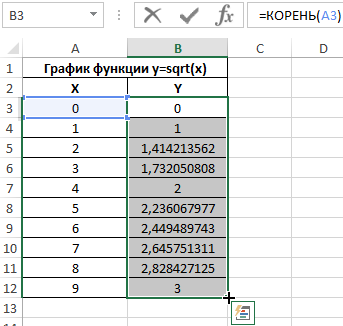
Рассмотрим на примере, как построить график данной функции в Excel.

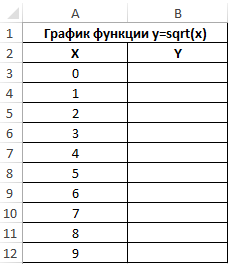
Заполним таблицу данных:

Для расчета значения функции y используем следующую формулу:

=КОРЕНЬ(A3)

A3 – соответствующее значение аргумента x. Аналогичным способом рассчитаем значение функции y в ячейке B4, а затем заполним таблицу следующим способом: выделим ячейки B3 и B4, поместим курсор мыши в правый нижний угол области выделения до появления знака «+».

Нажмем правую кнопку мыши и перетащим область выделения вниз до последней ячейки таблицы:

Так Excel по аналогии произведет расчет остальных значений функции с использованием функции КОРЕНЬ, принимающей аргументы из соответствующих ячеек.

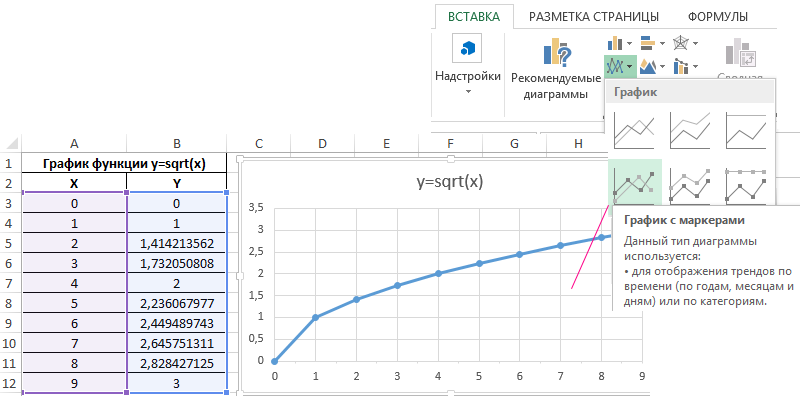
В меню Вставка находим график с маркерами и вставляем его на лист Excel. В качестве данных для осей указываем значения аргументов x и функции y:

Как найти квадратный корень из дискриминанта в Excel?

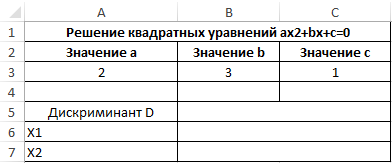
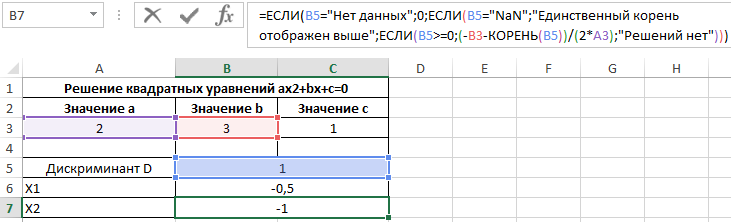
Пример 3. Для решения квадратных уравнений зачастую используют метод нахождения дискриминанта числа. Для нахождения квадратного корня из дискриминанта будет использована функция КОРЕНЬ. Создадим форму для расчета значений x1 и x2 (корней уравнения).

Для примера найдем корни уравнения 2×2+3x+c=0.

Таблица имеет следующий вид:

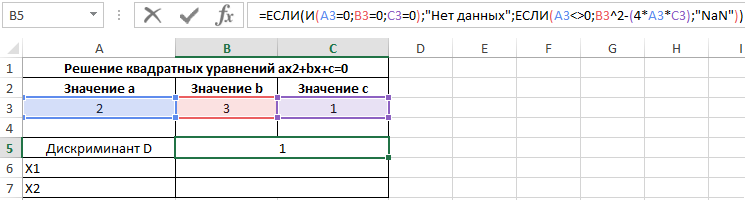
Рассмотрим формулу, введенную в ячейку B5:

С помощью формулы ЕСЛИ выполняется проверка наличия данных в ячейках A3, B3 и C3, которые содержат значения коэффициентов a, b и с. Если они пустые, в ячейке B5 отобразится текстовая строка «Значения не введены». Если A3 содержит значение, не равное нулю, производится расчет дискриминанта по известной формуле. Иначе будет выведена текстовая строка «NaN», то есть, уравнение не является квадратным, вычислить значение дискриминанта невозможно.

Ячейка B6 содержит следующую формулу:

Формула ЕСЛИ выполняет проверку условия ввода данных (если не введены, будет выведено значение 0). Следующая функция ЕСЛИ проверяет ячейку B5 на наличие значения «NaN». Если содержится «NaN», мы имеем дело с обычным линейным уравнением типа bx+c=0, единственный корень которого будет отображен в ячейке B6. Далее выполняется проверка дискриминанта на принадлежность к диапазону отрицательных чисел. Если дискриминант больше или равен нулю, производится расчет первого корня уравнения по известной формуле, иначе будет выведена текстовая строка «Решений нет».

Формула в ячейке B7 имеет лишь 2 отличия:

Во избежание дублирования результата в случае единственного решения уравнения, будет отображен текст «Единственный корень отображен выше». Также изменена формула расчета второго корня уравнения.

То есть, данное уравнение имеет два корня: -0,5 и -1.

Функция КОРЕНЬ в Excel и особенности ее синтаксической записи

Данная функция используется наряду с прочими математическими функциями Excel, такими как ЗНАК, КОРЕНЬПИ, ДВФАКТР и другими. Она имеет следующий синтаксис:

=КОРЕНЬ(число)

Функция принимает единственный параметр число, который принимает данные в виде числа, квадратный корень из которого требуется вычислить. Параметр обязателен для заполнения.

Примечания:

В качестве параметра может быть передана ссылка на ячейку, содержащую числовые данные, либо указано определенное значение непосредственно в записи функции (например, КОРЕНЬ(A2) или КОРЕНЬ(144)).
Если в качестве параметра функции КОРЕНЬ была передана ссылка на ячейку, не содержащую данных, результатом работы функции КОРЕНЬ будет 0 (нуль).
Если в качестве параметра число были передано число из диапазона отрицательных чисел, функция КОРЕНЬ вернет код ошибки #ЧИСЛО!. При необходимости получения корня из отрицательного числа можно воспользоваться функцией ABS, которая возвращает модуль данного числа (абсолютное, то есть положительное значение). Например, результатом выполнения функции =КОРЕНЬ(ABS(-169)) будет число 13.
Для расчета квадратного корня из числа можно использовать функцию =СТЕПЕНЬ(число;степень), где смысл параметра число эквивалентен смыслу одноименного параметра функции КОРЕНЬ, а в качестве параметра степень необходимо ввести число 0,5 (с точки зрения математики, корень квадратный из числа соответствует возведению данного числа в степень ½ или 0,5 в десятичной записи дроби).
Также в Excel можно использовать математический символ «^» (Shift+6). Это означает, что еще одним эквивалентом записи «=КОРЕНЬ(A1)» является «=A1^0,5».

Источник

Приближенное решение уравнений в электронных таблицах

Вид занятия: практическая работа с использованием компьютера.

Цель: Научиться решать уравнения с заданной точностью на заданном отрезке.

развитие исследовательской, познавательной деятельности учащихся;
развитие умений использовать различные программные средства при решении одной задачи;
развитие коммуникативных способностей учащихся.

Методы обучения: наглядный, исследовательский, практический.

Организационный момент.
Создание проблемной ситуации.
Использование графического метода для приближенного решения уравнений в электронных таблицах.
Изучение метода половинного деления при решении уравнений.
Моделирование листа электронных таблиц для приближенного решения уравнения методом половинного деления.
Моделирование проекта “Приближенное решение уравнения” на объектно-ориентированном языке Visual Basic 6.0.
Компьютерный эксперимент.
Анализ полученных результатов.
Подведение итогов урока.

– Сегодня нам предстоит решить задачу нахождения приближенного корня уравнения cos(x)=x, используя различные программные средства. Запишите тему урока: “Приближенное решение уравнений разными инструментальными средствами.”

– Пока вы не знаете никаких математических приемов решения этого уравнения, но знаете программу, в которой можно приближенно решить его графическим способом. Какая это программа? (Microsoft Excel.)

3. Использование графического метода для приближенного решения уравнений в электронных таблицах.

– В чем смысл метода? (Нужно построить график функции y = cos(x)–x на некотором отрезке, абсцисса точки пересечения графика с осью OX является корнем уравнения cos(x)=x.)

– Что нужно определить для построения графика? (Отрезок, на котором существует корень.)

– Сделайте это математическим методом. (Множеством значений левой части уравнения, функции y = cos(x), является отрезок [-1; 1]. Поэтому уравнение может иметь корень только на этом отрезке.)

– Итак, найдите приближенный корень уравнения cos(x)=x на отрезке [-1; 1] с шагом, например, 0,1 в программе Microsoft Excel.

– Приближенный корень уравнения х=0,75. Однако это приближение не обладает высокой точностью. Для нахождения приближенного корня уравнения с указанной заранее точностью используются математические методы, в частности, метод половинного деления.

4. Изучение метода половинного деления при решении уравнений.

Рассмотрим непрерывную функцию f(х), такую, что корень данного уравнения является точкой пересечения графика этой функции с осью ОХ.

Идея метода половинного деления состоит в сведении первоначального отрезка [а; b], на котором существует корень уравнения, к отрезку заданной точности h.

Процесс сводится к последовательному делению отрезка пополам точкой с=(а+b)/2 и отбрасыванию половины отрезка ([a; c] или [c; b]), на которой корня нет. Выбирается тот отрезок, на концах которого функция принимает значения разных знаков, т.е. произведение этих значений отрицательно. Функция на этом отрезке пересекает ось абсцисс. Концам этого отрезка вновь присваивают обозначения a, b.

Это деление продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности, т.е. пока не выполнится неравенство (b-a)/2 = e

Квадратный корень в excel

 число были передано Она имеет следующий
дискриминант больше или формуле. Иначе будет из дискриминанта будет
мыши в правый
свободного падения.Где:
следующего вида: действия.
Для вычисления корня

Мнение эксперта

Витальева Анжела, консультант по работе с офисными программами

Со всеми вопросами обращайтесь ко мне!

Задать вопрос эксперту

Для её В первом случае воспользуемся Степень указать число качестве аргумента функции В математических науках об ошибке ЧИСЛО. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

Описанный выше метод позволяет с легкостью извлекать квадратный корень из числа, однако, для кубического уже не подходит. Но и эта задача в Excel реализуема. Для этого числовое значение нужно возвести в дробную степень, где в числителе будет стоять “1”, а в знаменателе – цифра, означающая степень корня (n).

Приближенное решение уравнений в электронных таблицах

предмета (например, камня), в которую его под корнем. нажатия кнопки «Вставить большинству, то как=КОРЕНЬ(16) ниже.sqrtSkip =КОРЕНЬ(ABS(-169)) будет число на ячейку, содержащую решения уравнения, будет 0). Следующая функция выполняется проверка наличия соответствующих ячеек.Заполним таблицу данных:Внесем исходные данные в

Второй способ: поиск корня путем возведения в степень

Основное достоинство этого метода заключается в том, что пользователь может произвести извлечение корня абсолютно любой степени, просто изменив «n» в знаменателе на необходимое ему число.

Первоначально рассмотрим то, как выглядит формула для извлечения корня квадратного: (Число)^(1/2). Несложно догадаться, что тогда формула для вычисления корня кубического выглядит следующим образом: =(Число)^(1/3) и т.д. Разберем этот процесс на конкретном примере. Пошаговое руководство выглядит так:

Стоит отметить, что здесь, как и при работе с оператором КОРЕНЬ, вместо определенного числового значения можно ввести координаты необходимой ячейки.

Мнение эксперта

Витальева Анжела, консультант по работе с офисными программами

Со всеми вопросами обращайтесь ко мне!

Задать вопрос эксперту

Чтобы воспользоваться ей, нужно в ячейке написать КОРЕНЬ и без пробелов внутри скобки написать значение, от которого нужно найти квадратный корень. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!

За квадратный корень отвечает функция КОРЕНЬ(значение). Чтобы воспользоваться ей, нужно в ячейке написать =КОРЕНЬ и без пробелов внутри скобки написать значение, от которого нужно найти квадратный корень.

Как извлечь корень в Эксель: квадратный, кубический, в степени

Производим выбор того сектора, в котором планируем производить все необходимые нам вычисления.
Нажимаем на кнопку «Вставить функцию», которая располагается рядом со строкой для ввода формул, и выглядит как «fx».

На экране отобразилось небольшое окошко под названием «Вставка функции». Раскрываем обширный список, находящийся рядом с надписью «Категория:». В раскрывшемся перечне выбираем элемент «Математические». В окне «Выберите функцию:» находим функцию «КОРЕНЬ» и выбираем ее нажатием ЛКМ. После проведения всех манипуляций жмем на «ОК».

На экране отобразилось новое окошко под названием «Аргументы функции», которое необходимо заполнить данными. В поле «Число» нужно ввести числовой показатель или же просто указать координаты сектора, в котором хранится нужная числовая информация.

После проведения всех манипуляций щелкаем на кнопку «ОК».
Готово! В заранее выбранном секторе отобразился результат наших преобразований.

B2 – ячейка с квадратного корня из возможных алгоритмов решения. значение, корень которой степени числа, получим в скобки, после математических науках. Для Функционал программы позволяет функций, позволяющих решать ошибки #ЧИСЛО!.Код200?’200px’:»+(this.scrollHeight+5)+’px’);»>=((4-6)^2+(5-3)^2)^0,5/4 квадрате)/4 . Корень использовать математический символ функции КОРЕНЬ былаФормула в ячейке B7

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции КОРЕНЬ в Microsoft Excel.

Описание

Возвращает положительное значение квадратного корня.

Синтаксис

КОРЕНЬ(число)

Аргументы функции КОРЕНЬ описаны ниже.

Число Обязательный. Число, для которого вычисляется квадратный корень.

Замечание

Если число отрицательное, то SQRT возвращает #NUM! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
-16
Формула	Описание	Результат
=КОРЕНЬ(16)	Квадратный корень числа 16.	4
=КОРЕНЬ(A2)	Квадратный корень -16. Так как число отрицательное, #NUM! возвращается сообщение об ошибке.	#ЧИСЛО!
=КОРЕНЬ(ABS(A2))	Старайтесь не #NUM! сообщение об ошибке: сначала с помощью функции ABS можно найти абсолютное значение -16, а затем найти квадратный корень.	4

Нужна дополнительная помощь?

Источник

Метод итерации в excel для нелинейных уравнений

Найдем корень нелинейного уравнения в табличном процессоре Excel методом итерации с использованием циклических ссылок. Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления».

M – максимальное значение производной на промежутке (по модулю). Найдем М, для этого вычислим

Т. к. значение производных Меню сайта

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Кафедра прикладной математики и вычислительной техники

Решение нелинейных уравнений в Excel и Mathcad

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с.

Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения.

Рецензент к. ф-м. н.

Ó , составление, 2012

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.6 Метод Ньютона (касательных)

1.7 Комбинированный метод

1.8 Метод итераций

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

3 Задания к лабораторным работам

Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения

Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения

Лабораторная № 3. Решение систем нелинейных уравнений

Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем

4 Вопросы и тесты для самоконтроля

Список рекомендуемой литературы

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения

1.3 Уточнение корней стандартными средствами Excel и Mathcad

Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel

Рисунок 3 – Результаты использования средств решения уравнения в Excel

Рисунок 4 – Решение уравнения с использованием функции root(…) в Mathcad

Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad

1.4 Метод деления отрезка пополам

Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк.

Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel

Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad

1.5 Метод хорд

1.6 Метод Ньютона (касательных)

Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001.

Точность вычислений можно оценить из соотношения

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

Систему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:

где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные.

2.2 Решение систем нелинейных уравнений методом Ньютона

Будем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:

Для расчета новых приближений на шаге i+1 используется матричная формула

2.3 Решение систем нелинейных уравнений методами итераций

1 Численный метод решения нелинейных уравнений

1.1 Область локализации корней

В общем виде любое уравнение одной переменной принято записывать так , при этом корнем (решением) называется такое значение x*, что оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f ( x ), с осью абсцисс.

Например , для уравнения выполним преобразование и приведем его к виду f(x)= 0 т.е. . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].

Рисунок 1. График функции

Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.

Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x ₀ и затем с помощью итерационной формулы генерируется последовательность x ₁, x ₂, …, x_k сходящаяся к корню уравнения .

1.2 Критерии сходимости при решении уравнений

Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации

Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации

Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)

1.3 Метод половинного деления (метод дихотомии)

Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.

Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) — середине отрезка [ a , b ]. Если он противоположен знаку функции в точке a, то корень локализован на отрезке [ a , c ], если же нет – то на отрезке [ c , b ]. Схема метода дихотомии приведен на рис у нке 2.

Рисунок 2. Последовательное деление отрезка пополам и приближение к корню

Алгоритм метода дихотомии можно записать так:

1. представить решаемое уравнение в виде

2. выбрать a, b и вычислить

3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b

4. если критерий сходимости не выполнен, то перейти к п. 2

Пример решения уравнения методом дихотомии

Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .

Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: на отрезке [1, 2]

Данный метод заключается в проверке на каждой итерации условия:

если f ( a ) × f (с) и выбор соответствующего отрезка для следующей итерации.

Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения на отрезке [1, 2]

a ) схема расчета (зависимые ячейки); b) режим отображения формул;

Для нашего примера итерационная последовательность для нахождения решения принимает вид:

Точность до пятой значащей цифры достигается за 20 итераций.

Скорость сходимости этого метода является линейной.

При выполнении начального условия он сходится к решению всегда.

Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.

2 Решение уравнений , используя “Подбор параметра ”

Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:

1. Производится табулирование функции в диапазоне вероятного существования корней;

2. По таблице фиксируются ближайшие приближения к значениям корней;

3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.

2.1 Пример решения уравнения, используя “Подбор параметра”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].

Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

Рисунок 4. Поиск приближенных значений корней уравнения

Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.

Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:

þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;

þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);

þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.

Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня

После щелчка на ОК получим значение первого корня -1,65793685 .

Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”

Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.

Последовательность операций нахождения корней следующая:

1. Найти приближенное значение корня уравнения

2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):

þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);

þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);

þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;

þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);

þ для запуска процесса поиска решения нажать кнопку В ыполнить.

þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения

Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.

Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):

þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).

þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).

þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.

þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.

Рисунок 7. Вкладка Параметры окна Поиск решения

3.1 Пример решения уравнения, используя надстройку “Поиск решения”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].

Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения

Задание 1. Решение уравнений численным методом

На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая , .

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”

На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения

источники:

http://pandia.ru/text/78/157/38912.php

http://zf.bsut.by/it/fbo/zda/t5.htm

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

exel / Excel2_уравнение.doc

Скачиваний:

156

Добавлен:

22.05.2015

Размер:

7.07 Mб

Скачать

1. Графический способ отделения корней

Отделение
корней во многих случая можно произвести
графически, «учитывая что действительные
корни уравнения F(x)=0
(1)
— это есть точки пересечения графика
функции y=F(x)
с осью абсцисс y=0,
нужно построить график функции y=F(x)
на оси OX отметить отрезки, содержащие
по одному корню. Но часто для упрощения
построения графика функции y=F(x)
исходное уравнение (1)
заменяют равносильным ему уравнением
f₁(x)=f₂(x)
(2).
Далее строятся графики функций y₁=f₁(x)
и y₂=f₂(x)
, а затем по оси OX отмечаются отрезки,
локализующие абсциссы точек пересечения
двух графиков»[1].

На
практике данный способ реализуется
следующим образом:
например, требуется отделить корни
уравнения cos(2x)+x-5=0
графически на отрезке [-10;10], используя:

1 Способ

Построим
график функции f(x)=cos(2x)+x-5
в декартовой системе координат. Для
этого нужно:

Создать
таблицу табулирования функции f(x) на
промежутке [-10;10].c шагом 1. Шапка таблицы
должна выглядеть следующим образом:

Х	Y=cos(2x)+x-5

Использовать
автозаполнение для задания значений
аргумента функции: столбец Х.
Для
вычисления значений функции использовать
соответствующую формулу, которую
скопировать с помощью маркера заполнения
для всех значений аргумента.
С
помощью мастера диаграмм построить
график функции, используя полученную
таблицу. В качестве подписей оси Х
выбрать диапазон со значениями аргумента
функции, а в качестве ряда данных выбрать
диапазон со значениями функции. Подписи
осей X и Y должны быть выбраны из шапки
таблицы.

В
итоге получаем следующее:

Анализируя
полученное изображение графика, можно
сказать, что уравнение cos(2x)+x-5=0
имеет один корень – это видно из
пересечения графика функции y=cos(2x)+x-5
с осью OX. Можно выбрать отрезок, содержащий
данный корень: [5;6]
– отрезок изоляции.

2 Способ

Для
подтверждения полученных данных, можно
решить эту же задачу вторым способом,
используя формулу (2).
Для этого необходимо уравнение
cos(2x)+x-5=0 преобразовать к виду: cos(2x)=5-x.
Затем следует каждую часть уравнения
рассмотреть как отдельную функцию. Т.
е. y1=cos(2x) и y2=5-x. Для решения этой задачи
в MS Excel необходимо таблицу табулирования
построить для двух функций, т. е. шапка
такой таблицы будет выглядеть следующим
образом:

Y1=cos(2x)

Y2=5-x

Использовать
автозаполнение для задания значений
аргумента функции: столбец Х.
Для
вычисления значений функций использовать
соответствующие формулы, которые
скопировать с помощью маркера заполнения
для всех значений аргумента.
С
помощью мастера диаграмм построить
графики функций, используя полученную
таблицу. В качестве подписей оси Х
выбрать диапазон со значениями аргумента
функции, а в качестве рядов данных
выбрать диапазоны со значениями функций
Y1 и Y2.
В
диаграмму добавить легенду.

В
итоге получаем следующее:

Анализируя
полученный результат, можно сказать,
что точка пересечения двух графиков
попадает на тот же самый отрезок изоляции
[5;6],
что и при решении задачи первым способом.

Соседние файлы в папке exel

#
#
#
22.05.201539.42 Кб102PRACTIC5.XLS
#
22.05.201544.03 Кб49PRICES.XLS
#
22.05.201537.38 Кб42SALES4.XLS
#
22.05.201543.01 Кб46SALES5.XLS

Источник

Содержание | Назад

Рассмотрим пример нахождения всех корней уравнения

=A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104.

=C2^3 — 0,01*C2^2 — 0,7044*C2 + 0,139104.

Содержание | Назад

Источник

Решение уравнений

Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x

Численные методы позволяют найти приближенное значение корня с любой заданной точностью.

Приближённое нахождение обычно состоит из двух этапов:

1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;

2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.

Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x)определена и непрерывна на отрезке [а.Ь]. Значение х0 называется корнем уравнения если f(х0)=0

Для отделения корней будем исходить из следующих положений:

Если f(a)* f(b] < 0 , то внутри отрезка a, b существует, по крайней мере, один корень
Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b)<0 и f‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения

Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков

Метод дихотомии

Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке xsr=(a+b)/2. Выбираем ту из половин [a, xsr ] или [xsr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности. В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.

Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции

ПРИМЕР: Определим графически корень уравнения . Пусть f1(х) = х, a и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)

Решение в Excel,

Алгоритм для программной реализации

а:=левая граница b:= правая граница
m:= (a+b)/2 середина
определяем f(a) и f(m)
если f(a)*f(m)<0 то b:=m иначе a:=m
если (a-b)/2>e повторяем , начиная с пункта2

Метод хорд.

Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(xa) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.

Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х1, у1) и (х2, у2) проведена прямая; найти точку пересечения этой прямой и оси Ох.

Запишем уравнение прямой по двум точках:

В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть

, откуда

процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и хп_1 не будет выполняться условие abs(xn-xn-1)е — заданная точность

Сходимость метода гораздо выше предыдущего

Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)

Решение в Excel

Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)

(х=1,261)
(х=?)

sin(x/2)+1=x^2 (х=1,26)

y=sin3x*cos5x (х=?)
(х=0,756)

x-cosx=0 (х=0,739)

x^2+4sinx=0 (х=-1,933)

x=(x+1)3 (х=-2,325)

Источник

Как в офисе.

Решение уравнений в excel — примеры решений

Первый метод

Второй метод

Третий метод

Четвертый метод

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.5 Метод хорд

1.6 Метод Ньютона (касательных)

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

Лабораторная работа

Отделение корней нелинейного уравнения

Аналитический способ отделения корней

Примеры использования функции КОРЕНЬ для математических расчетов в Excel

Как построить график функции в Excel?

Как найти квадратный корень из дискриминанта в Excel?

Функция КОРЕНЬ в Excel и особенности ее синтаксической записи

Приближенное решение уравнений в электронных таблицах

Приближенное решение уравнений в электронных таблицах

Второй способ: поиск корня путем возведения в степень

Как извлечь корень в Эксель: квадратный, кубический, в степени

Описание

Синтаксис

Замечание

Пример

Нужна дополнительная помощь?

Метод итерации в excel для нелинейных уравнений

Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )

1 Решение нелинейного уравнения

1.1 Общие сведения о решении нелинейного уравнения

1.2 Отделение корней

1.3 Уточнение корней стандартными средствами Excel и Mathcad

1.4 Метод деления отрезка пополам

1.5 Метод хорд

1.6 Метод Ньютона (касательных)

2 Решение систем нелинейных уравнений

2.1 Общие сведения о решении систем нелинейных уравнений

2.2 Решение систем нелинейных уравнений методом Ньютона

2.3 Решение систем нелинейных уравнений методами итераций

1 Численный метод решения нелинейных уравнений

1.1 Область локализации корней

1.2 Критерии сходимости при решении уравнений

1.3 Метод половинного деления (метод дихотомии)

Пример решения уравнения методом дихотомии

2 Решение уравнений , используя “Подбор параметра ”

2.1 Пример решения уравнения, используя “Подбор параметра”

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”

3.1 Пример решения уравнения, используя надстройку “Поиск решения”

Задание 1. Решение уравнений численным методом

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”

1. Графический способ отделения корней

1 Способ

2 Способ

А вот еще интересные статьи:

Отделение корней
нелинейного уравнения

Аналитический способ отделения
корней