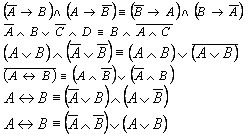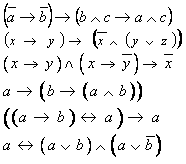Фев 04 2021
Вроде простая вещь — нужно вычислить результат для нескольких булевых переменных
Читаем основную статью
Компьютер
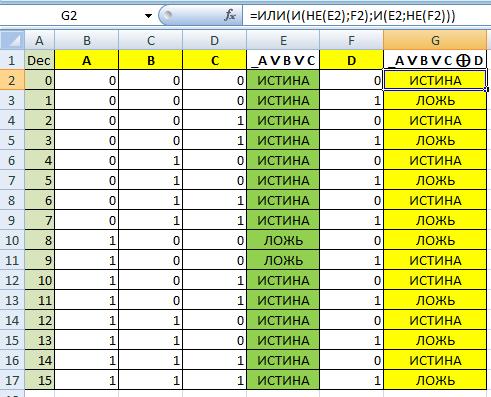
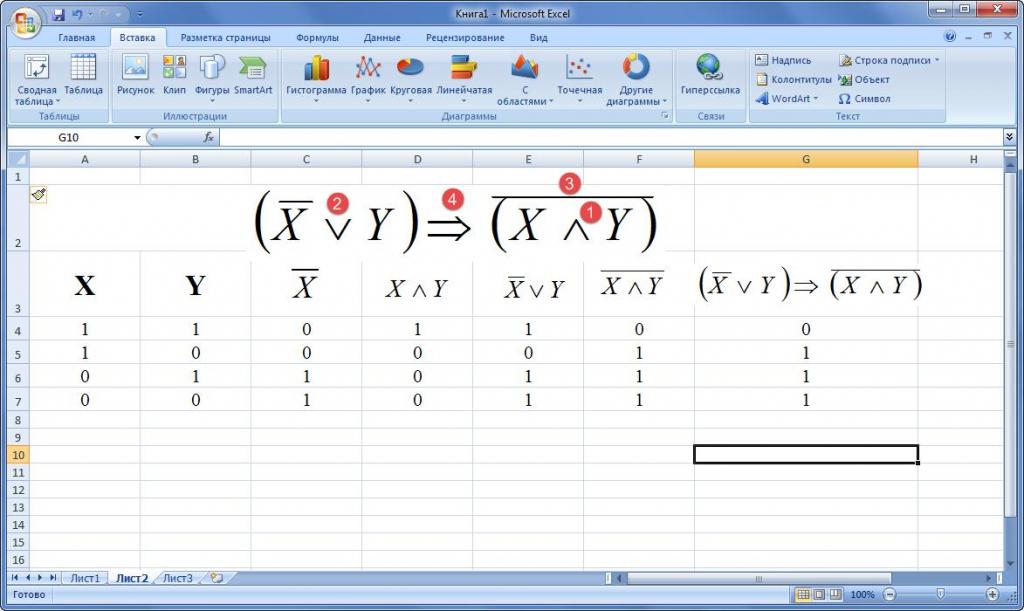
Вроде всё просто. Но вот такой пример вида _A ∨ B ∨ C ⊕ D
Переводим на русский язык (с математического языка) — нужно сделать таблицу истинности для выражения
не A или B или C иск.или D
для всех вариантов переменных A,B.C.D, которые могут принимать значения «Истина» / «Ложь»
Или на английском (для программирования) = not.A.or.B.or.C.xor.D
Задача на булеву алгебру не сложная — но у нас четыре переменных и 16 строк в таблице (да, 24 = 16). А если таких переменных будет 5, то в таблице будет 32 строки.
Но у нас есть Excel (Execute Cell), который прекрасно понимает формулы логики. Достаточно правильно написать формулу для одной строки — и потом мышкой перетащить эту формулу на остальные строки. Готово!
Итак по частям.
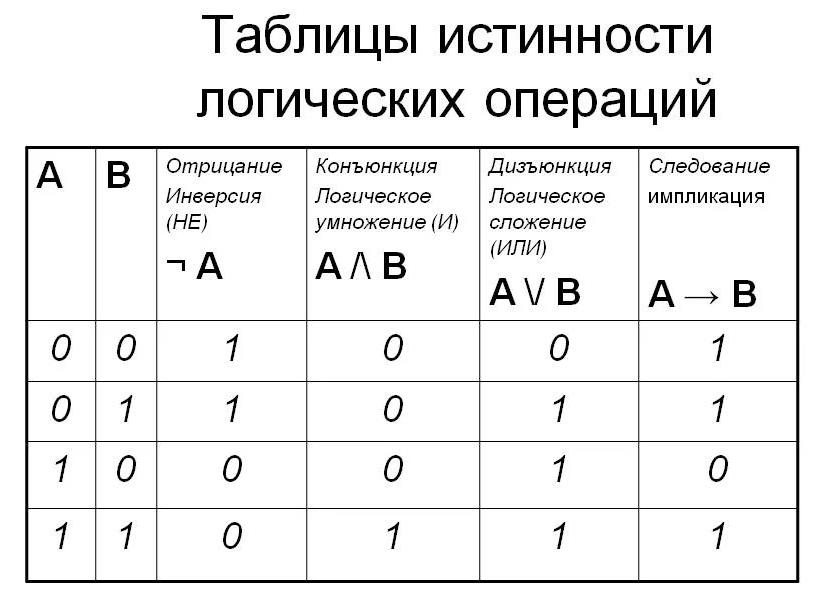
Логическая операция это операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логическая связка это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
Логические операции
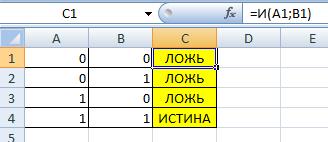
Логическая операция И (Конъюнкция)
Конъюнкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логическое «И», логическое умножение, иногда просто «И»
И таблица истинности (AND таблица истинности)
=И(A1;B1)
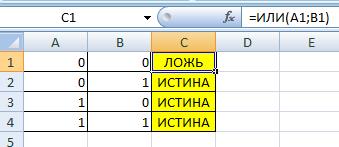
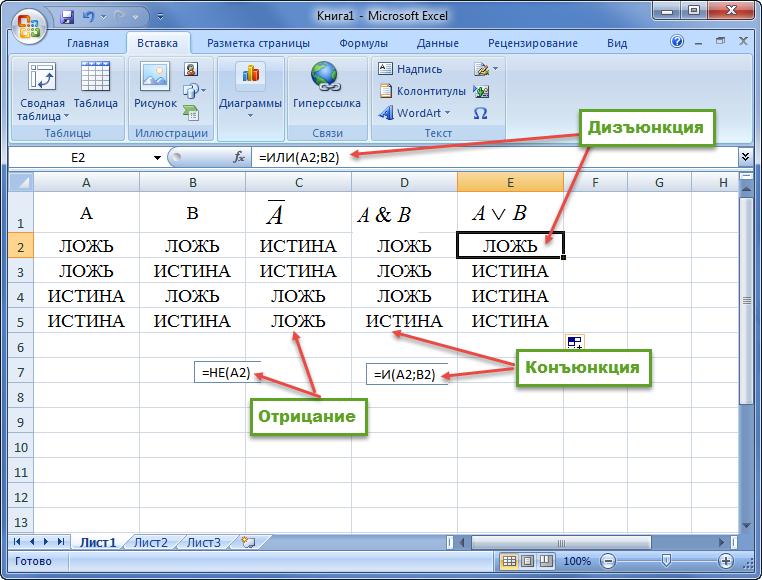
Логическая операция ИЛИ (Дизъюнкция)
Дизъюнкция (от лат. disjunctio — «разобщение») — логическое сложение, логическое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»
ИЛИ таблица истинности (OR таблица истинности)
=ИЛИ(A1;B1)
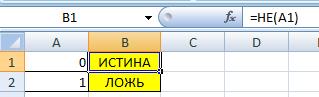
Логическая операция отрицания (Инверсия)
Инверсия (от лат. inversio «переворачивание; перестановка») — отрицание — переворачивание смысла, замена «белого» «чёрным»
НЕ таблица истинности (NOT таблица истинности)
=НЕ(A1)
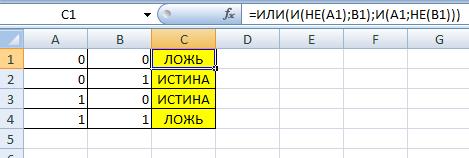
Логическая операция XOR (исключающее ИЛИ)
XOR таблица истинности
В Excel 2007 её нет.
В более современных версиях она есть. Но мы её можем собрать самостоятельно.
=ИЛИ(И(НЕ(A1);B1);И(A1;НЕ(B1)))
Логические связки
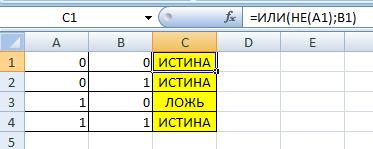
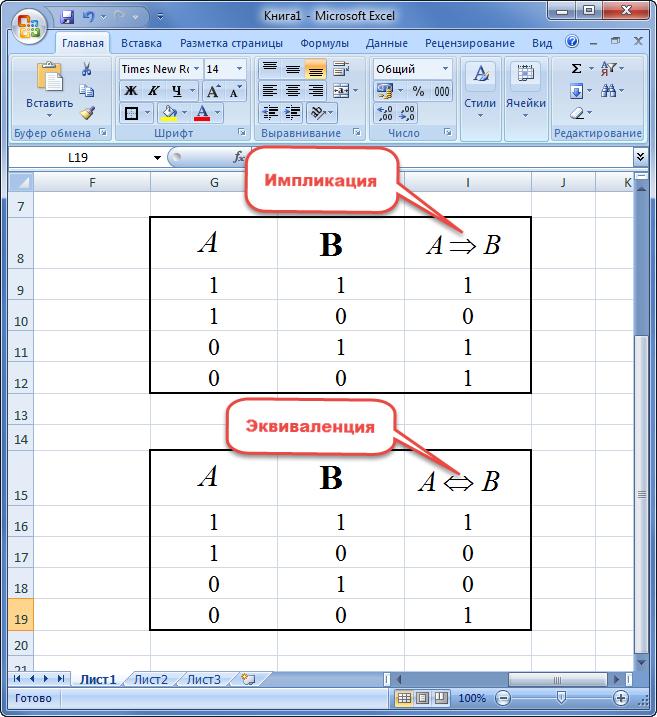
Логическая связка Импликация (прямая)
Логическая связка как A → B
используем аналог _A V B
=ИЛИ(НЕ(A1);B1)
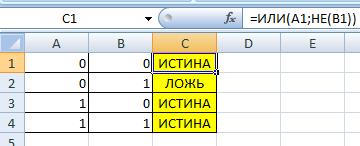
Логическая связка Импликация (обратная)
Логическая связка как A ← B
используем аналог A V _B
=ИЛИ(A1;НЕ(B1))
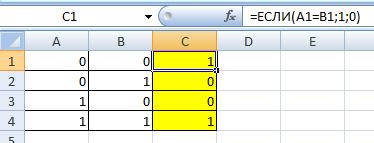
Логическая связка ТОЖДЕСТВО
Используем ЕСЛИ, чтобы логическая связка получилась
=ЕСЛИ(A1=B1;1;0)
или вывод текстом
=ЕСЛИ(A1=B1;"ИСТИНА";"ЛОЖЬ")
Собираем таблицу истинности
Не обязательно собирать всё в одной ячейке. Можно сделать столбцы для промежуточных вычислений.
Для нашего примера _A ∨ B ∨ C ⊕ D
Удобно.
Последние публикации
- Статьи от: Автор
- Рубрика: Блог
- Сортировка: дата публикации по убыванию
Классический вход Windows 7
Публикация 2 года назад
Как это было в Windows XP Для входа в систему нужно указать: пользователь (login)
пароль В Windows 7 сделали по умолчанию стандартный вход в систему Мышкой выбираем пользователя и вводим только пароль (если он установлен). Как вернуть классический вход в систему Windows 7 и зачем это нужно? Для работы на локальной машине — конечно удобнее стандартный вход. А вот если Вы подключаетесь к удаленной машине через RDP — то ввода только пароля недостаточно. Читаем статью RDP — удаленный рабочий стол Большое количество ботов со всего мира подберет Ваш пароль достаточно быстро (в логах будет по 5-10 попыток в секунду). Читаем статью Включаем шифрование…
(Читать полностью…)
Процессоры AMD FX и их «ядра»

Публикация 2 года назад
Немного маркетинга в тему — ядра процессоров AMD FX и ядра процессоров Intel AMD FX (AM3+) — хорошие были процессоры. Но есть нюанс. AMD использовала хитрую терминологию — «ядра» и «модули». Это была вершина маркетинга 
Одно…
(Читать полностью…)
Загадочная «маска подсети» — это просто
Публикация 2 года назад
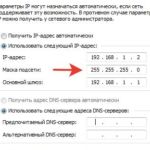
Многие видели в Windows свойства адаптера сети при ручной настройке Многие даже понимают, что IP-адрес 192.168.1.1 — это запись в десятичной форме 32-х бит адреса IP v4 с разбивкой на оксеты (по 8 бит). Что такое «маска подсети»?
Которая 255.255.255.0. И зачем она нужна? Посмотрим в таком же двоичном виде — легко видеть, что это 24 единицы подряд Это просто так айтишники шутят 
(Читать полностью…)
Вычисляем большие числа

Публикация 2 года назад
Самое известное большое число googol — отсюда собственно название Google 10100 = это 1 единица и 100 нулей Хорошо. А например, 2512 — это сколько? Калькулятор Windows говорит, что это 1,3 * 10154 Тоже неплохо, да и больше чем googol на 54 порядка 
(Читать полностью…)
Как соединить два роутера проводом?
Публикация 3 года назад
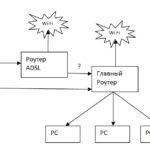
Предположим, у нас есть «Главный роутер», который управляем всеми нашими устройствами PC. И еще есть: у «Главного роутера» второй WAN-порт
бесхозный ADSL роутер Простой вопрос — как сделать резервирование интернета? Что бы при отсутствии основного интернета можно было подключить и использовать «Роутер ADSL»? Основная статья про сеть здесь Варианты в лоб: использовать только «Роутер ADSL» — но это придется к нему переподключать все конечные ПК
и сетку Wi-Fi придется перестраивать для переподключения мобильных устройств Нехорошо 
(Читать полностью…)
Как не надо устанавливать SSD M.2

Публикация 3 года назад
Иногда вот такая жесть бывает при установке SSD M.2. Небольшой изгиб, так сказать. Основная статья про M.2 тут Интерфейс NVMe и разъемы M.2 и U.2 Как это получилось? Обычно так бывает при самостоятельной сборке ПК из новых комплектующих. SSD M.2 устанавливается под 45% в разъем на плате и потом прижимается винтиком, которые вкручивается в другой винтик на материнской плате. Но почему этот основной винтик «пенек» может отсутствовать на материнской плате? Вот тут хорошо видно проблему 
или кладет все…
(Читать полностью…)
Как набрать немецкие умляуты (umlaut) на обычной клавиатуре в России?

Публикация 3 года назад
Будем разбираться с немецкими умляутами Делаем свой набор горячих клавиш (hotkey) для умляутов
Самый удобный вариант 
R Alt A
Ä
ä O
Ö
ö U
Ü
ü S
ẞ
ß Здесь символы A, O, U и S — это не буквы, а кнопки на клавиатуре. Как это сделать? Используем программу QuickTextPaste — в ней можно завязать не только отдельные буквы, и целые части текста. Настройки хранятся в C:UsersNameAppDataRoamingQuickTextPasteQuickTextPaste.ini Использование простое: добавляем комбинацию клавиш
…
(Читать полностью…)
В настоящее время применение информационных
технологий становится неотъемлемой частью
образовательного процесса. Компьютер наиболее
полно удовлетворяет дидактическим требованиям и
позволяет адаптировать процесс обучения к
индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в
процесс обучения и диагностики, позволяют
упростить процесс отработки навыков и умений и
оценки знаний учащихся.
В данной работе рассматривается применение
табличного процессора MS Excel при изучении основ
логики.
Существует множество задач, в которых исходные
и результатные данные должны быть представлены в
табличной форме. Электронные таблицы
представляют собой удобный инструмент для
автоматизации таких вычислений. Решения многих
вычислительных задач на ЭВМ, которые раньше
можно было осуществить только путем
программирования, стало возможно реализовать.
Использование математических формул в
электронных таблицах позволяет представить
взаимосвязь между различными параметрами
некоторой реальной системы. Основное свойство
электронных таблиц – мгновенный пересчет формул
при изменении значений входящих в них операндов.
Благодаря этому свойству, таблица представляет
собой удобный инструмент для организации
численного эксперимента:
- подбор параметров,
- прогноз поведения моделируемой системы,
- анализ зависимостей,
- планирование.
В электронных таблицах предусмотрен также
графический режим работы, который дает
возможность графического представления (в виде
графиков, диаграмм) числовой информации,
содержащейся в таблице.
В процессе изучения алгебры логики учащиеся
знакомятся с такими понятиями как: высказывание,
таблицы истинности, логические функции и
логические операции. Алгебра логики является
разделом математической логики, в которой
изучаются методы доказательства истинности (1)
или ложности (0) сложных логических конструкций,
составленных из простых высказываний, на основе
истинности или ложности последних. Для
закрепления полученных знаний возможно
использование табличного процессора MS Excel и его
функций.
Для реализации функций булевой алгебры
используются логические функции: ЕСЛИ, И, ИЛИ, НЕ,
ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel
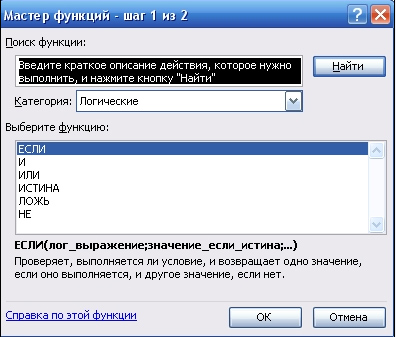
используется мастер функций (Вставка Функция…), в котором отображается
имя функции, ее описание и аргументы.
Рисунок 1. Окно мастера функций
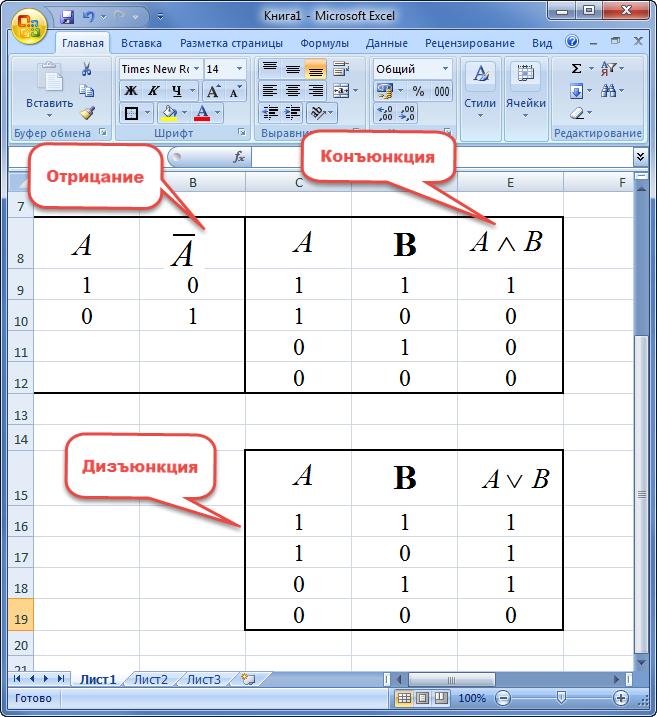
Первоначально следует создать таблицу
основных логических операций:
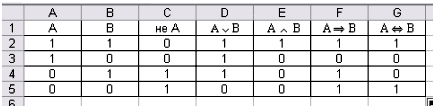
Рисунок 2. Таблица истинности основных
логических операций
При составлении таблицы истинности
используются следующие формулы:
- Инверсия: =ЕСЛИ(A2=1;0;1);
- Дизъюнкция: =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0);
- Конъюнкция: =ЕСЛИ(И(A2=1;B2=1);1;0);
- Импликация: =ЕСЛИ(И(A2=1;B2=0);0;1);
- Эквивалентность: =ЕСЛИ(A2=B2;1;0).
В последующей работе данная таблица может
использоваться учащимися как основа для
выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая
работа.
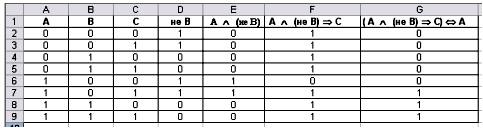
Задание: Построить таблицу истинности для
формулы (A
B
C)
A, используя MS Excel.
Алгоритм:
- Определить количество наборов входных
переменных, по формуле: Q = 2n, где n –
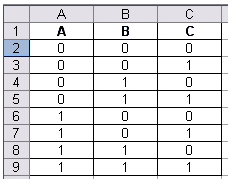
количество переменных. Q = 23 = 8. - Внести в таблицу все наборы входных переменных:
Рисунок 3. Исходные данные
- Определить количество логических операций и
порядок их выполнения:
- Заполнить столбцы результатами выполнения
логических операций в обозначенной
последовательности.
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
в G2: =ЕСЛИ(F2=A2;1;0).
Заполнение остальных строк произвести путем
копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для
закрепления не только материала математической
логики, но и для основ теории вероятностей и
математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности
равносильность формул.
Определить являются ли формулы тавтологиями.
Встречаются электронные таблицы, в которых необходимо применить логические функции, логические схемы разного порядка. На помощь приходит программный пакет Microsoft Excel. Он способен не только вычислить логическое значение выражения, но и провести сложные математические расчеты.
Что такое Excel?
Программный продукт, предназначенный для работы с электронными таблицами. Создан корпорацией Microsoft и подходит почти к любой операционной системе. Здесь можно использовать как формулы для нахождения результатов, так и построить графики и диаграммы различных видов.

Пользователь применяет в Excel не только логические функции, но и математические, статистические, финансовые, текстовые и т. д.
Особенности Excel
Сферы применения программного продукта разнообразны:
- Рабочий лист Excel представляет собой готовую таблицу, поэтому у пользователя отпадает необходимость в проведении расчетов по приведению документа к надлежащему виду.
- Программный пакет предлагает использовать булевы функции, а также тригонометрические, статистические, текстовые и т. д.
- На основе вычислений Excel строит графики и диаграммы.
- Поскольку программный пакет содержит большую библиотеку математических и статистических функций, школьники и студенты могут использовать его для выполнения лабораторных и курсовых работ.
- Пользователю полезно применять возможности Excel для домашних и личных расчетов.
- В программный продукт встроен язык программирования VBA, способный облегчит жизнь бухгалтеру при автоматизации рабочего процесса небольшой фирмы.
- Электронная таблица Excel выступает и как база данных. Полностью функционал реализуется только с версии 2007 года. В ранних продуктах было ограничение по количеству строк.
- При создании отчетности различной направленности Excel приходит на помощь, поскольку помогает создать сводную таблицу.
Логические операторы Excel

Под логическими выражениями понимаются данные, необходимые для записи элементов, в которых конъюнкция и дизъюнкция, а также другие операторы, сопоставляют числа, формулы, текст. С их помощью сообщение записывают в символьном виде с указанием действия.
Логические функции (иначе называемые булевы) в качестве элементов задействуют числа, текст, ссылки с адресами ячеек.
Изучить подробнее каждый оператор и его синтаксис можно несколькими способами:
- Вызвать «Мастер функций».
- Воспользоваться справкой Microsoft через F1.
- В версиях Excel от 2007 года изучить состав каждой категории на панели инструментов.
Булева алгебра

Основателем логики высказываний (иное название раздела математики) является Д. Буль, занимавшийся в юности переводами работ древнегреческих философов. Именно оттуда он почерпнул знания и предложил ввести специальные обозначения для высказываний: 1 – Истина, 0 – Ложь.
Булевой алгеброй называют раздел математики, изучающий высказывания, рассматривающий их в качестве логических значений и совершаемые над ними операции. Любое утверждение можно закодировать, а затем использовать, манипулировать им для доказательства истинности или ложности.
Булевой функцией называют f(x1, x2, … , xn), от n переменных, если функция или любой из ее операторов принимает значения только из множества {0;1}. Законы алгебры логики применяются при решении задач, в программировании, кодировании и т. д.
Отображать булеву функцию можно следующими способами:
- словесным (утверждением, записанным в текстовом виде);
- табличным;
- численным;
- графическим;
- аналитическим;
- координатным.
Функция «И»
Оператор «И» является конъюнкцией в программном пакете Excel. Иначе она называется логическим умножением. Обозначается обычно ∧, &, * или знак между операндами вовсе опускается. Функция нужна для определения правдивости введенного выражения. В булевой алгебре конъюнкция принимает значения из множества, и результат вычисления также записывается в него. Логическое умножение бывает:
- бинарным, поскольку содержит 2 операнда;
- тернарным, если имеется 3 множителя;
- n-арным, если множество содержит n операндов.
Решить пример можно через согласование с правилом либо через создание таблицы истинности. Если выражение содержит несколько операндов, удобнее воспользоваться программным пакетом Excel для второго способа решения, поскольку весь процесс при вычислениях вручную будет громоздким.
Результатом вычислений могут быть:
- Истина: если все аргументы правдивы.
- Ложь: если все критерии ложны или хотя бы один из них.
Операторы «И» и «ИЛИ» могут содержать до 30 критериев.
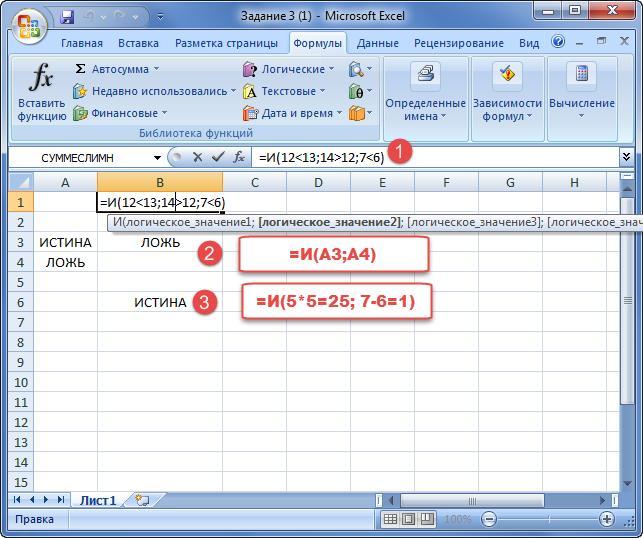
Пример.
1) Необходимо определить истинность вписанных данных. Очевидно, что последний пример, заключенный в скобках, неверен с математической точки зрения, поэтому функция выдаст ответ «Ложь».
2) В двух ячейках указаны противоположные значения. Функция «И» выдает результат «Ложь», поскольку один из аргументов неправдив.
3) Заданы арифметические действия. Необходимо проверить их истинность. Данный оператор выдает ответ «Истина», поскольку с арифметической точки зрения все верно.
Функция «ИЛИ»
Оператор «ИЛИ» в категории «Логические функции» является дизъюнкцией, т. е. позволяет получить правдивый ответ в некатегоричной форме. Иное название оператора в булевой алгебре: логическое сложение. Обозначают: ∨, +, «или». Переменные берут значения из множества и туда же записывается ответ.
Результатом вычислений бывают:
- Истина: если хотя бы один из аргументов или все они являются правдивыми.
- Ложь: если все критерии ложны.
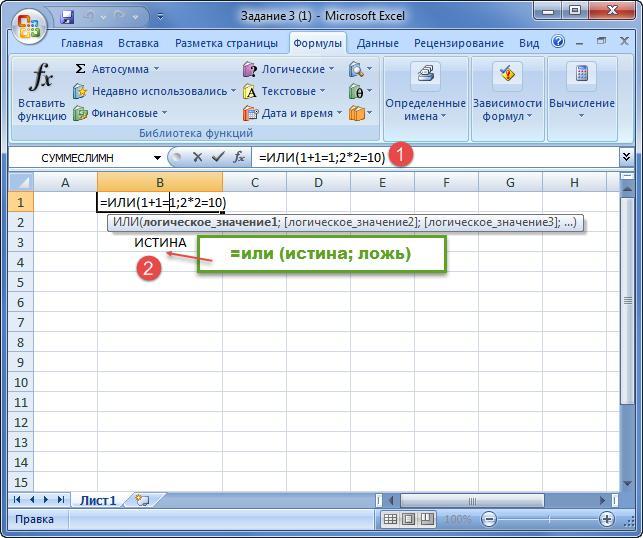
Пример.
1) Дизъюнкция в Excel проверяет не только логические выражения, но и математические на правильность. Так, в конкретном случае оба результата ложны с арифметической точки зрения, поэтому ответ – «Ложь».
2) Оператор выдает ответ «Истина», поскольку один из аргументов правдивый, другой ложный. Это является допустимым критерием для дизъюнкции.
Функция «ЕСЛИ»
В группе «Логические функции» почетное место занимает оператор «ЕСЛИ». Функция необходима для получения результата, если информация правдива, и другого итога, если данные ложны.
- В условном операторе возможна проверка до 64 условий за 1 раз.
- Если один из критериев – массив, тогда функция проверяет каждый элемент.
- Если ответ ложный, но в формуле не прописано, чему должен равняться итог в случае «False», тогда оператор выдает результат, равный 0.
Пример.
Дано:
- наименование товара;
- его цена за 1 единицу;
- количество приобретенного товара;
- стоимость.
Необходимо рассчитать графу «К оплате». Если стоимость покупки превышает 1000 рублей, то покупателю предоставляется скидку в 3 %. В противном случае графы «ИТОГО» и «К оплате» одинаковы.
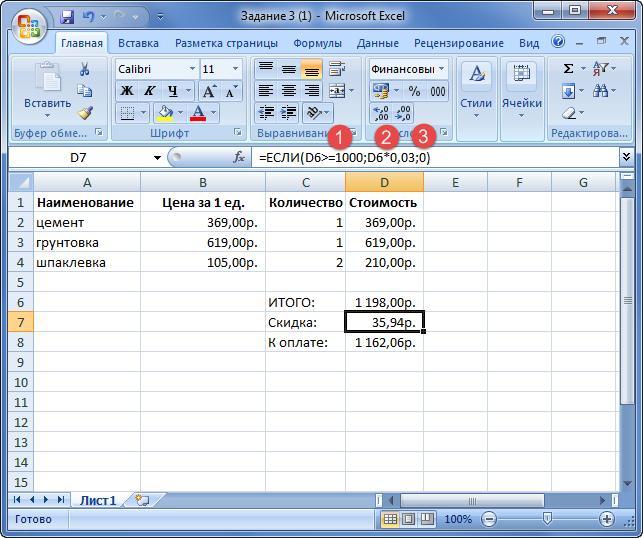
1) Проверка условия: стоимость превышает 1000 рублей.
2) В случае истинности критерия стоимость умножается на 3 %.
3) В случае ложности высказывания результат «К оплате» не отличается от «ИТОГО».
Проверка нескольких условий
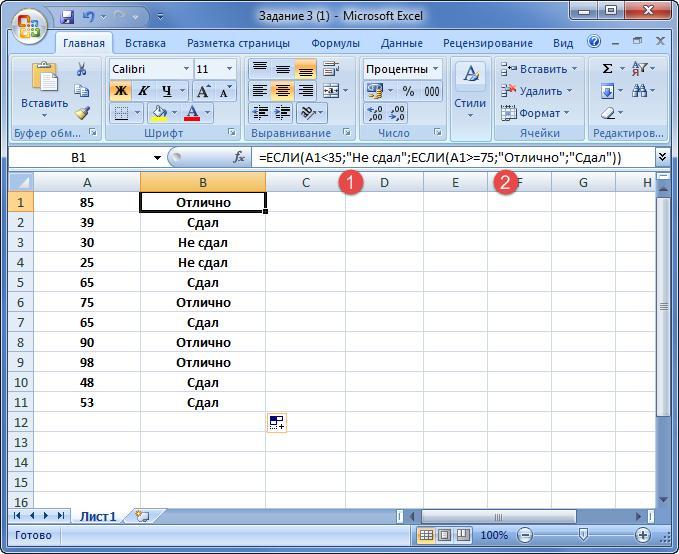
Имеется таблица, в которой указаны баллы за экзамен и отметка преподавателя.
1) Нужно проверить, меньше ли сумма баллов 35. Если ответ истинный, то результат работы – «Не сдал».
2) Если предыдущее условие ложное, сумма баллов >35, оператор переходит к проверке следующего аргумента. Если значение в ячейке >=75, то рядом присваивается «Отлично». При иных вариантах функция вернет «Сдал».
Несмотря на то что оператор «Если» работает с логическими значениями, он прекрасно действует и с числами.
Пример.
Даны:
- имена продавцов;
- их продажи.
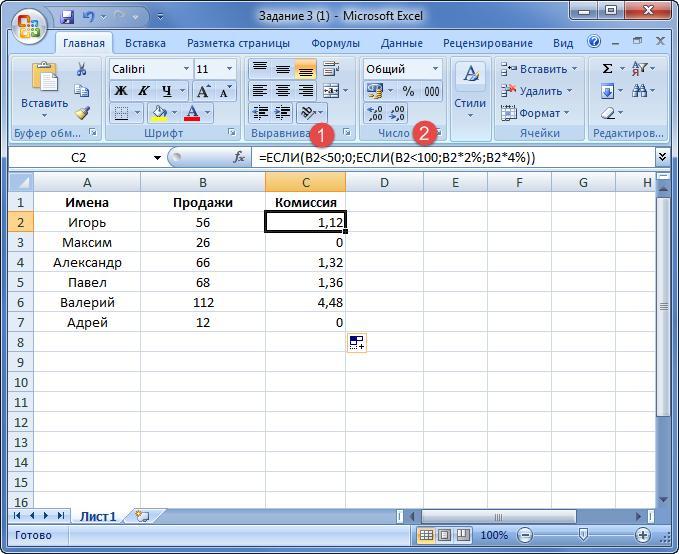
Следует вычислить, кому из продавцов какая комиссия причитается:
- если количество продаж менее 50 тысяч, то процент не начисляется;
- если объем сделок варьируется в пределах 50-100 тысяч, то комиссия составляет 2 %;
- если количество продаж более 100 тысяч, то премия выписывается в размере 4 %.
Под цифрой 1 отмечен первый блок «ЕСЛИ», где проверяется на истинность. Если условие ложно, то выполняется блок 2, где прописываются дополнительно еще 2 критерия.
Функция «ЕСЛИОШИБКА»
Булевы функции дополняются данным оператором, поскольку он способен вернуть некий результат, если в формуле имеется ошибка. Если все верно, «ЕСЛИОШИБКА» возвращает результат вычислений.
Функция «ИСТИНА» и «ЛОЖЬ»
Булевы функции в Excel не обходятся без оператора «ИСТИНА». Он возвращает соответствующее значение.
Оператором, обратным по действию «ИСТИНЕ» является «ЛОЖЬ». Обе функции не имеют аргументов и крайне редко используются в качестве самостоятельного примера.
Оператор «НЕ»
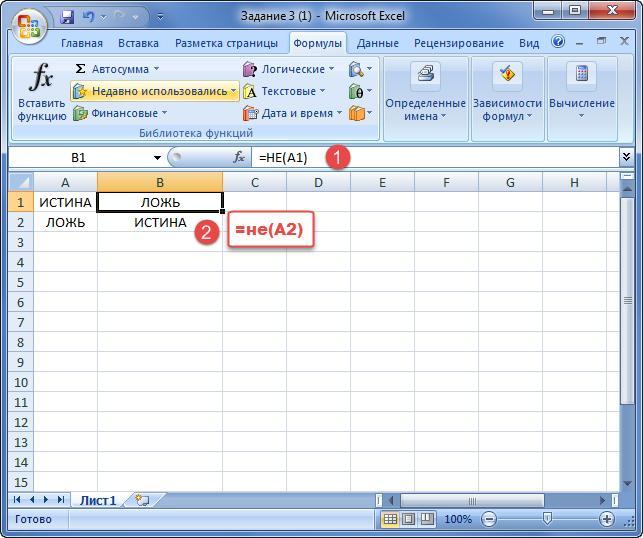
Все логические функции в Excel можно опровергнуть посредством оператора «НЕ». Введенное значение при использовании данной процедуры будет в результате противоположным.
Пример.
Очевидно, что оператор выдает ответ, противоположный изначальным данным.
Минимизация логических функций
Это явление напрямую связано с созданием схемы или цепи. Это выражается через ее сложность и стоимость, пропорциональность числа логических операций и количество вхождений аргументов. Если использовать аксиомы и теоремы логики, можно упростить функцию.
Существуют специальные алгоритмические методы минимизации. Благодаря им пользователь способен самостоятельно упростить функцию быстро и без ошибок. Среди таких методов выделяют:
- карты Карно;
- метод Квайна;
- алгоритм импликантных матриц;
- метод Квайна-Мак-Класки и т. д.
Если количество аргументов не превышает 6, тогда пользователю для наглядности лучше использовать метод карт Карно. В противном случае применяется алгоритм Квайна-Мак-Класки.
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
- штрих Шеффера;
- стрелка Пирса.
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
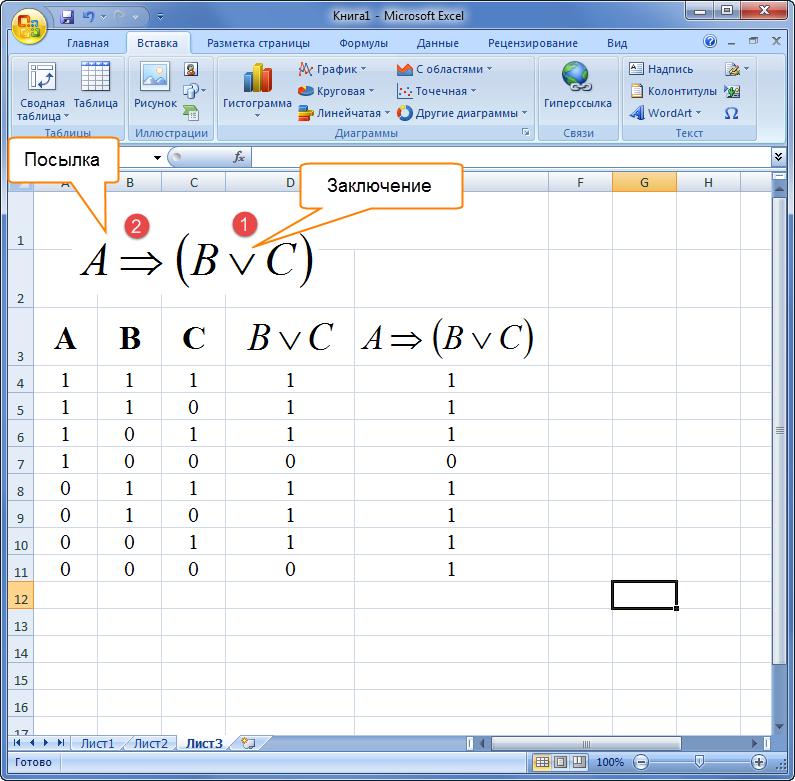
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|---|---|
|
И |
Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА. |
|
Функция BYCOL |
Применяет ЛЯМБДА к каждому столбцу и возвращает массив результатов. |
|
Функция BYROW |
Применяет ЛЯМБДА к каждой строке и возвращает массив результатов. |
|
ЛОЖЬ |
Возвращает логическое значение ЛОЖЬ. |
|
ЕСЛИ |
Выполняет проверку условия. |
|
ЕСЛИОШИБКА |
Возвращает введенное значение, если вычисление по формуле вызывает ошибку; в противном случае возвращает результат вычисления. |
|
ЕСНД |
Возвращает значение, которое задается, если выражение принимает значение #Н/Д. В противном случае возвращает результат выражения. |
|
УСЛОВИЯ |
Проверяет соответствие одному или нескольким условиям и возвращает значение для первого условия, принимающего значение ИСТИНА. |
|
ЛЯМБДА-функция |
Создание пользовательских многократно используемых функций и их вызов по понятному имени |
|
Функция «LET» |
Присваивает имена результатам вычислений |
|
Функция MAKEARRAY |
Возвращает вычисляемый массив указанной строки и размера столбца, применяя ЛЯМБДА-выражение. |
|
|
Возвращает массив, сформированный путем сопоставления каждого значения в массивах с новым значением путем применения ЛЯМБДА для создания нового значения. |
|
НЕ |
Меняет логическое значение своего аргумента на противоположное. |
|
ИЛИ |
Возвращает значение ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА. |
|
|
Уменьшает массив до накопленных значений, применяя ЛЯМБДА к каждому значению и возвращая общее значение в накопителе. |
|
|
Сканирует массив, применяя ЛЯМБДА к каждому значению и возвращая массив с каждым промежуточным значением. |
|
ПЕРЕКЛЮЧ |
Сравнивает выражение со списком значений и возвращает результат, соответствующий первому совпадающему значению. Если совпадений не выявлено, может возвращаться указанное значение по умолчанию. |
|
ИСТИНА |
Возвращает логическое значение ИСТИНА. |
|
ИСКЛИЛИ |
Возвращает логическое исключающее ИЛИ всех аргументов. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
См. также
Функции Excel (по категориям)
Функции Excel (по алфавиту)