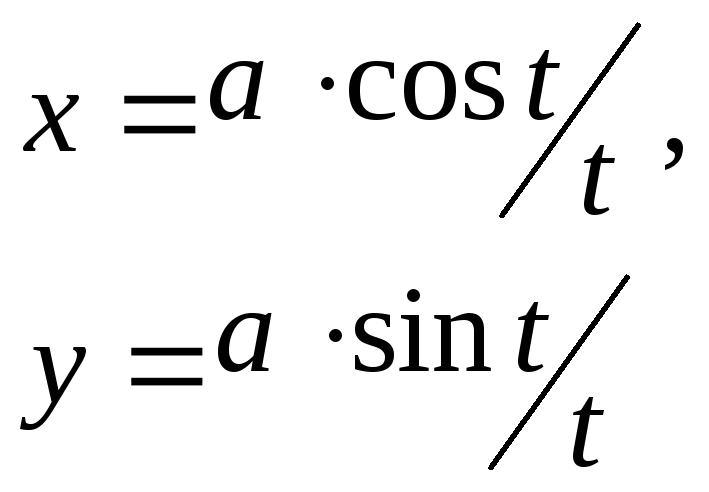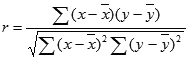Конхоида никомеда в excel - Word и Excel - помощь в работе с программами

Помогаю со студенческими работами здесь

построить конхоиду Никомеда
Построить кривую по параметрическому представлению (конхоида Никоме-
да):
x = a + l cost, y = a…

Построить конхоиду Никомеда
Необходимо построить конхоиду Никомеда
r=a*sec (varphi )pm b
Только вот не получается что-то…

Построить график конхоиды Никомеда
Помогите построить график конхоиды Никомеда:
уравнения: x=a+l*cos(t), y=a*tg(t)+l*sin(t)…

Построить графики Конхоида Никомеда
Постройте кривые по заданному параметрическому представлению.
Конхоида Никомеда:
x=a + fcos(t) ;…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

Образец
выполнения

Построение
графиков EXEL

Вариант
1.

Построить 5 графиков
функций отдельно.

Уравнения циклоиды
заданы в параметрическом виде:

где t
меняется от 0 до

с шагом 0,1.

=
1,0, 1,25, 1,5, 1,75, 2,0.

Вариант
2.

Построить 6 графиков
функции отдельно.

Уравнение кривой
«Локон Аньези»

где x
меняется от –6 до 6 с шагом 0,1.

=
1,2,3,4,5,6.

Вариант
3.

Построить 6 графиков
функции отдельно.

Уравнения кривой
«Декартов лист»
заданы в параметрическом виде:

где t
меняется от –6 до 6 с шагом 0,1, кроме точки
t=-1.

=1,2,3,4,5,6.

Вариант
4.

Построить 6 графиков
функции отдельно.

Уравнения циссоиды
заданы в параметрическом виде:

где t
изменяется от –6 до 6 с шагом 0,1.

=1,2,3,4,5,6.

Вариант
5.

Построить 6 графиков
функции отдельно.

Уравнения строфоиды
заданы в параметрическом виде:

где t
изменяется от –6 до 6 с шагом 0,1.

=1,2,3,4,5,6.

Вариант
6.

Построить 6 графиков
функции отдельно.

Уравнения кривой
«Конхоида Никомеда»
заданы в параметрическом виде:

где t
изменяется от
до
с
шагом 0,05, кроме точки
.

b=3,
=1,2,3,4,5,6.

Вариант
7.

Построить 6 графиков
функции отдельно.

Уравнения кривой
«Улитка Паскаля»
заданы в параметрическом виде:

где t
изменяется от 0 до
с
шагом 0,05. b=3,
=1,2,3,4,5,6.

Вариант
8.

Построить 6 графиков
функции отдельно.

Уравнения циклоиды
заданы в параметрическом виде:

,где t
изменяется от 0 до
с
шагом 0,1.

=2,
=0,4;
0,7; 1,0; 1,3; 1,6; 2,0.

Вариант
9.

Построить 6 графиков
функции отдельно.

Уравнения эпициклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,05.

b=1,2,3,4,5,6.

=1.

Вариант
10.

Построить 6 графиков
функции отдельно.

Уравнения эпициклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,1.

b=1,2,3,4,5,6.
=5.

Вариант
11.

Построить 4 графика
функции отдельно.

Уравнения эпициклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,1.

a	2	3	5	7
b	7	5	3	2

Вариант
12.

Построить 6 графиков
функции отдельно.

Уравнения
гипоциклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,05.

b=2,3,4,5,6,11.

=1.

Вариант
13.

Построить 3 графика
функции отдельно.

Уравнения
гипоциклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,1.

b=1,5;
3,5; 5,5.
=1.

Вариант
14.

Построить 6 графиков
функции отдельно.

Уравнения эпициклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,05.

b=4.

=1.

=0,4;
0,7; 1,0; 1,3; 1,6; 2,0.

Вариант
15.

Построить 6 графиков
функции отдельно.

Уравнения
гипоциклоиды
заданы в параметрическом виде:

,где

изменяется от 0 до

с шагом 0,05.

b=4.

=1.

=0,4;
0,7; 1,0; 1,3; 1,6; 2,0.

Вариант
16.

Построить 3 графика
функции отдельно.

Уравнения
гиперболической
спирали заданы в параметрическом
виде:

где t
изменяется от -6 до 6 с шагом 0,1, кроме
точки t=0.

=1,3,6.

Вариант
17.

Построить 5 графиков
функции отдельно.

Уравнения эллипса
заданы в параметрическом виде:

где t
изменяется от 0 до

с шагом 0,05.

=7.
b=1,4,7,10,13.

Вариант
18.

Построить 3 графика
функции отдельно.

Уравнения гиперболы
заданы в параметрическом виде:

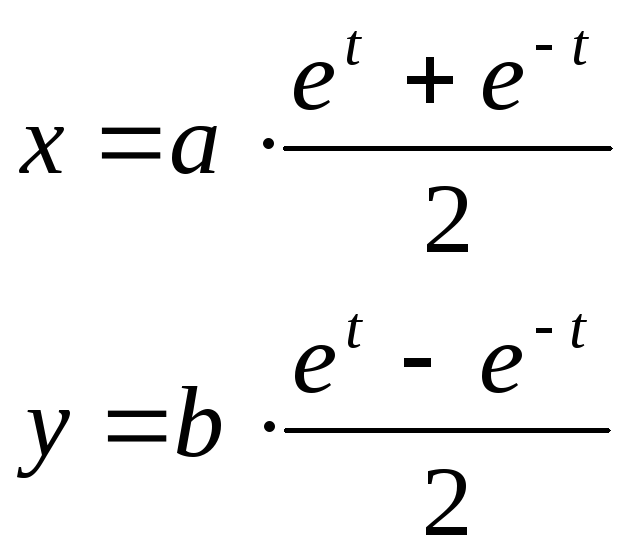
где t
изменяется от -2 до 2 с шагом 0,1.

=0,1;
1,5; 3, b=3.

Вариант
19.

Построить 6 графиков
функции отдельно.

Уравнения эвольвенты
окружности заданы в параметрическом
виде:

,где t
изменяется от -10 до 10 с шагом 0,1.

=0,1;
0,5; 1; 1,5; 2; 2,5.

Вариант
20.

Построить 5 графиков
функции отдельно.

Уравнения окружности
заданы в параметрическом виде:

где t
изменяется от -10 до 10 с шагом 0,1.

— координаты центра
окружности, R – радиус.

x₀	0	1	-8	4	-5,5
y₀	0	3	-5	-4	3
R	5	8	10	4	20

Вариант
21.

Построить 6 графиков
функции отдельно.

Уравнения кардиоиды
заданы в параметрическом виде:

где t
изменяется от -5 до 5 с шагом 0,1.

=5,
9,12,30,45,50.

Вариант
22.

Построить 5 графиков
функций отдельно.

Уравнения циклоиды
заданы в параметрическом виде:

где t
меняется от 0 до

с шагом 0,1.

=
1,0, 1,25, 1,5, 1,75, 2,0.

Вариант
23.

Построить 6 графиков
функции отдельно.

Уравнение кривой
«Локон Аньези»

где x
меняется от –6 до 6 с шагом 0,1.

=
1,2,3,4,5,6.

Вариант
24.

Построить 6 графиков
функции отдельно.

Уравнения кривой
«Декартов лист»
заданы в параметрическом виде:

где t
меняется от –6 до 6 с шагом 0,1, кроме точки
t=-1.

=1,2,3,4,5,6.

Вариант
25.

Построить 6 графиков
функции отдельно.

Уравнения циссоиды
заданы в параметрическом виде:

где t
изменяется от –6 до 6 с шагом 0,1.

=1,2,3,4,5,6.

Вариант
26.

Построить 6 графиков
функции отдельно.

Уравнения строфоиды
заданы в параметрическом виде:

где t
изменяется от –6 до 6 с шагом 0,1.

=1,2,3,4,5,6.

Вариант
27.

Построить 6 графиков
функции отдельно.

Уравнения кривой
«Конхоида Никомеда»
заданы в параметрическом виде:

где t
изменяется от
до
с
шагом 0,05, кроме точки
.

b=3,
=1,2,3,4,5,6.

Соседние файлы в папке Задание_Excel

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование RSQ
в Microsoft Excel.

Описание

Возвращает квадрат коэффициента корреляции Пирсона для точек данных в аргументах «известные_значения_y» и «известные_значения_x». Дополнительные сведения см. в статье Функция PEARSON. Значение квадрата R показывает, насколько дисперсии y связана с дисперсией x.

Синтаксис

КВПИРСОН(известные_значения_y;звестные_значения_x)

Аргументы функции КВПИРСОН описаны ниже.

Известные_значения_y Обязательный. Массив или диапазон точек данных.
Известные_значения_x Обязательный. Массив или диапазон точек данных.

Замечания

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, приводят к возникновению ошибки.
Если аргументы известные_значения_y и известные_значения_x пусты или указанное в них количество число точек данных не совпадает, функция КВПИРСОН возвращает значение ошибки #Н/Д.
Если known_y и known_x содержат только 1 точку данных, RSQ возвращает #DIV/0! значение ошибки #ЗНАЧ!.
Коэффициент корреляции Пирсона (r) вычисляется с помощью следующего уравнения:

где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Функция КВПИРСОН возвращает значение r2, являющееся квадратом коэффициента корреляции.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Известные значения y	Известные значения x
2	6
3	5
9	11
1	7
8	5
7	4
5	4
Формула	Описание	Результат
=КВПИРСОН(A3:A9; B3:B9)	Квадрат значения корреляции Пирсона между точками данных в диапазоне A3:A9 и B3:B9.	0,05795

Нужна дополнительная помощь?

Источник

uses graphABC;
var x0,y0,r,x1,y1:integer;
    a1,a2,a3,l1,l2,l3,fn,fk,t,xr,yr:real;
begin
fn:=-pi/2; {начальный угол}
fk:=3*pi/2;{конечный}
x0:=windowwidth div 2;
y0:=windowheight div 2;
line(0,y0,windowwidth,y0);
line(x0,0,x0,windowheight);
{графики при l<a,l=a,l>a}
a1:=3;l1:=1;
a2:=3;l2:=6;
a3:=5;l3:=5;
r:=20;{масштабирование}
t:=fn;
while t<=fk do
 begin
  if abs(cos(t))>0.001 then
   begin
    xr:=a1+l1*cos(t);
    yr:=a1*sin(t)/cos(t)+l1*sin(t);
    x1:=x0+round(r*xr);
    y1:=y0-round(r*yr);
    setpixel(x1,y1,clGreen);
    xr:=a2+l2*cos(t);
    yr:=a2*sin(t)/cos(t)+l2*sin(t);
    x1:=x0+round(r*xr);
    y1:=y0-round(r*yr);
    setpixel(x1,y1,clBlue);
    xr:=a3+l3*cos(t);
    yr:=a3*sin(t)/cos(t)+l3*sin(t);
    x1:=x0+round(r*xr);
    y1:=y0-round(r*yr);
    setpixel(x1,y1,clRed);
   end;
  t:=t+0.001;
 end;
setfontsize(11);
setfontcolor(clGreen);
textout(30,50,'l=1 a=3');
setfontcolor(clBlue);
textout(30,70,'l=6 a=3');
setfontcolor(clRed);
textout(30,90,'l=5 a=5');
end.

Источник

1. Исторические сведения. Никомед, древнегреческий ученый, жил в 250-150 гг. до н. э. Линию, названную им конхоидой, по сходству ее с раковиной (PAQ на рис. 485) он ввел для графического решения задачи о разделении данного угла а на три равные части (трисекция угла).

Как мы теперь знаем, эта задача решается с помощью линейки и циркуля только при специальном подборе угла а например, при Так, задача о трисекции угла неразрешима, если пользоваться только линейкой и циркулем, т. е. если строить только прямые и окружности. Однако задача решается, если привлечь еще и другие линии, — в частности конхоиду. Для ее построения Никомед сконструировал специальный инструмент (конхоидограф).

2. Определение и построение. Даны: точка О (полюс), прямая (основание) и отрезок Из полюса О (рис. 485) проводим произвольную прямую пересекающую основание в точке На прямой откладываем в обе стороны от отрезки Геометрическое место точек мы теперь называем конхоидой Никомеда. Линия, описываемая точкой, лежащей на продолжении отрезка за точку на рис. 485) называется внешней ветвью конхоиды; линия, описываемая другой точкой ( на рис. 485), — внутренней ветвью.

Замечание. Сам Никомед (а также позднейшие авторы вплоть до конца 17 в.) именовал конхоидой линию, называемую сейчас внешней ветвью. Внутренняя ветвь рассматривалась как особая линия и называлась «второй», «третьей» или «четвертой» конхоидой в зависимости от особенностей ее формы (см. ниже).

3. Уравнение в прямоугольной системе (начало координат — в полюсе ось абсцисс направлена по лучу точка В — проекция полюса на основание):

где есть расстояние от полюса до основания.

Строго говоря, это уравнение представляет фигуру, состоящую из двух ветвей конхоиды и полюса О,

Рис. 485

который может и не принадлежать определенному выше геометрическому месту (см. рис. 487).

Уравнение в полярной системе (О — полюс; ОХ — полярная ось):

где меняется от какого-либо значения до При этом точка описывает обе ветви конхоиды.

При прохождении через значение точка скачком переходит с внешней ветви на внутреннюю («уходит в бесконечность» по направлению «вверх», а появляется «снизу»). Аналогично совершается переход при внутренней ветви на внешнюю.

В отличие от (1) уравнение (2) представляет фигуру, содержащую только те точки, которые удовлетворяют определению конхоиды.

Параметрические уравнения:

4. Особенности формы. Конхоида симметрична относительно прямой последняя пересекает конхоиду помимо точки О в двух точках (вершины). Основание асимптота как для внутренней, так и для внешней ветви. Форма конхоиды (внутренней ее

ветви) существенно зависит от соотношения между отрезками а и

1) Когда (рис. 485), внутренняя ветвь имеет петлю ; точка О — узловая.

Угловой коэффициент касательных в узловой точке:

Для построения касательных в точке О достаточно засечь на основании точки дугами радиуса I из центра О.

Наибольший поперечник петли:

Ему соответствует абсцисса и полярный угол определяемый формулой На рис. 485, где имеем

2) Когда петля внутренней ветви стягивается к полюсу О и превращается в точку возврата (рис. 486), касательная в этой точке совпадает с

3) Когда внутренняя ветвь не проходит через плюс О (рис. 487); последний является изолированной точкой линии (1).

5. Точки перегиба. На внешней ветви — две точки перегиба (см. рис. 485—487). На внутренней ветви точки перегиба на рис. 487) имеются лишь в том случае, когда полюс является изолированной точкой. Абсциссу пары точек и абсциссу пары точек можно найти из уравнения

8. Радиусы кривизны в точках :

Так, при

9. Площадь между асимптотой и одной из ветвей конхоиды (внешней или внутренней) бесконечна. Площадь петли:

Так, при (см. рис. 485)

10. Обобщенные конхоиды. Взяв вместо прямой линии какую-либо кривую а в остальном полностью сохранив определение конхоиды Никомеда, получим новую линию, называемую конхоидой линии относительно полюса О.

К числу обобщенных конхоид принадлежит, в частности, улитка Паскаля (см. § 508).

Источник

1

Построение графиков кривых с помощью компьютерных технологий Работу выполнили : учитель информатики Огийко С.В. и ученица 10 информатико-математического профиля Ясевич Т год, МОУ «Лицей 1 г.Петрозаводска

2

Конхоида Никомеда Конхоидой данной кривой называется кривая, которую можно получить при увеличении или уменьшении радиуса-вектора каждой точки данной кривой на постоянный отрезок l. Конхоида Никомеда (x-a) 2 (x 2 +y 2 )- l 2 x 2 =0 Конхоида Никомеда – конхоида прямой линии, то есть геометрическое место точек M, для которых OM=OP± r (внешняя ветвь для «+», внутренняя ветвь для «-») (см. рисунок) Уравнение в декартовой системе координат: (x-a) 2 (x 2 +y 2 ) – r 2 x 2 = 0 в параметрической форме: x = a + r cosφ y = a tg φ + r sin φ

3

1) фрагмент программы на языке программирования Паскаль h:=pi/180; f:=-3; readln(a,r); while f

4

Улитка Паскаля Улитку Паскаля можно определить как конхоиду окружности OM=OP±r (полюс лежит на окружности) (см. рисунок). Улитка Паскаля (x 2 +y 2 -ax) 2 =l 2 (x 2 +y 2 ) Уравнение кривой в прямоугольной декартовой системе координат: (x 2 + y 2 – ax) 2 = r 2 (x 2 + y 2 ) в параметрической форме: x = a cos 2 φ + r cos φ y = a sin φ* cos φ + r sin φ

5

1) фрагмент программы на языке программирования Паскаль h:=pi/180; f:=0; readln(a,r); while f

6

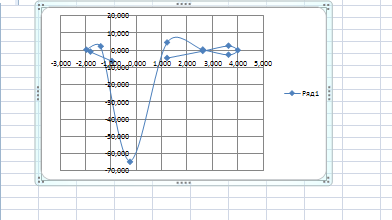
2) в электронных таблицах а=80 r = 10

7

Циклоидальные кривые Пусть некоторая кривая катится без скольжения по другой кривой. При этом любая точка, неизменно связанная с первой кривой, описывает новую линию. Среди кривых, образованных таким способом, выделяют кривые, являющиеся траекториями точки, неизменно связанной с окружностью, которая катится без скольжения по второй окружности. Полученные при этом линии называют циклоидальными. Циклоидальные кривые могут быть как алгебраическими, так и трансцендентными. Рассмотрим некоторые примеры алгебраических циклоидальных кривых.

8

Эпициклоида Эпициклоида – кривая, описываемая точкой окружности, которая катится без скольжения по другой окружности извне (см. рисунок). В параметрической форме уравнение эпициклоиды имеет вид: где A – радиус неподвижной окружности; a – радиус подвижной окружности; φ = COx. Вид кривой зависит от отношения:

9

1) фрагмент программы на языке программирования Паскаль h:=pi/180; f:=0; readln(A,a0); while f

10

Гипоциклоида Это — кривая, описываемая точкой окружности, которая катится без скольжения по другой окружности внутри нее (см. рисунок). Уравнение гипоциклоиды, координаты вершин – те же, что и для эпициклоиды с заменой «+» на «-».

11

1) фрагмент программы на языке программирования Паскаль h:=pi/180; f:=0; readln(A,a0); while f

12

Виды циклоид Удлиненные и укороченные : — эпициклоиды (эпитрохоиды) — гипоциклоиды (гипотрохоиды) Кардиоида Кривая Штейнера –прямой двулистник –прямой трилистник –однолистник Астроида

13

Другие виды кривых Кривая Кассини Лемниската Бернулли Каппа Синусоидальные спирали «Розы», или кривые Гвидо Гранди «Колоски» –трисектриса Лоншама –трисектриса Маклорена Кривые Ламе Параболические и гиперболические кривые

Источник

Образец выполнения

Построение графиков EXEL

Вариант 1.

Вариант 2.

Вариант 3.

Вариант 5.

Вариант 6.

Вариант 7.

Вариант 8.

Вариант 9.

Вариант 11.

Вариант 12.

Вариант 13.

Вариант 14.

Вариант 15.

Вариант 16.

Вариант 17.

Вариант 18.

Вариант 19.

Вариант 20.

Вариант 21.

Вариант 22.

Вариант 23.

Вариант 24.

Вариант 25.

Вариант 26.

Вариант 27.

Описание

Синтаксис

Замечания

Пример

Нужна дополнительная помощь?

А вот еще интересные статьи:

Образец
выполнения

Построение
графиков EXEL

Вариант
1.

Вариант
2.

Вариант
3.

Вариант
5.

Вариант
6.

Вариант
7.

Вариант
8.

Вариант
9.

Вариант
11.

Вариант
12.

Вариант
13.

Вариант
14.

Вариант
15.

Вариант
16.

Вариант
17.

Вариант
18.

Вариант
19.

Вариант
20.

Вариант
21.

Вариант
22.

Вариант
23.

Вариант
24.

Вариант
25.

Вариант
26.

Вариант
27.