Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Иногда требуется изменить направление, в котором располагаются ячейки. Это можно сделать путем копирования и вставки и применения команды «Транспонировать». Но в этом случае образуются повторяющиеся данные. Чтобы такого не происходило, можно вместо этого ввести формулу с функцией ТРАНСП. Например, на следующем изображении показано, как расположить горизонтально ячейки с A1 по B4 с помощью формулы =ТРАНСП(A1:B4).
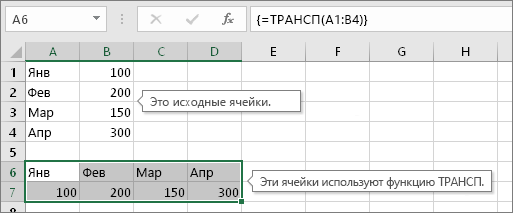
Примечание: Если у вас есть текущая версия Microsoft 365, вы можете ввести формулу в левую верхнюю ячейку диапазона вывода, а затем нажать ввод, чтобы подтвердить формулу как формулу динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Шаг 1. Выделите пустые ячейки
Сначала выделите пустые ячейки. Их число должно совпадать с числом исходных ячеек, но располагаться они должны в другом направлении. Например, имеется 8 ячеек, расположенных по вертикали:
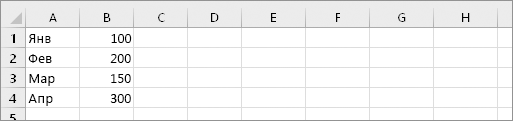
Нам нужно выделить 8 ячеек по горизонтали:
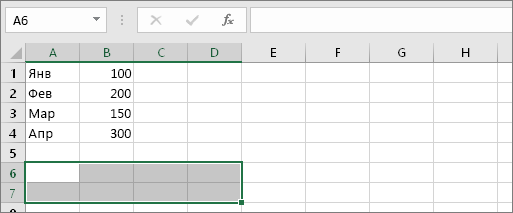
Так будут располагаться новые ячейки после транспонирования.
Шаг 2. Введите =ТРАНСП(
Не снимая выделение с пустых ячеек, введите =ТРАНСП(
Лист Excel будет выглядеть так:
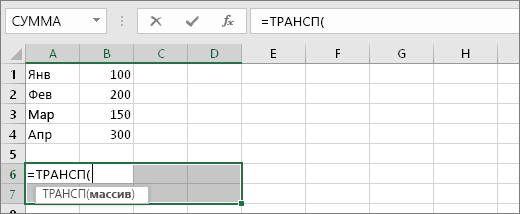
Обратите внимание на то, что восемь ячеек по-прежнему выделены даже несмотря на то, что мы начали вводить формулу.
Шаг 3. Введите исходный диапазон ячеек
Теперь введите диапазон ячеек, которые нужно транспоннять. В этом примере мы хотим транспоннять ячейки с A1 по B4. Поэтому формула для этого примера будет такой: =ТРАНСП(A1:B4) — но не нажимайте ввод! Просто остановите ввод и перейдите к следующему шагу.
Лист Excel будет выглядеть так:
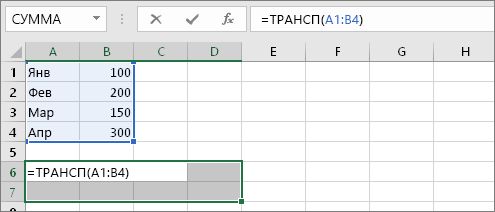
Шаг 4. Нажмите клавиши CTRL+SHIFT+ВВОД
Теперь нажмите клавиши CTRL+SHIFT+ВВОД. Зачем это нужно? Дело в том, что функция ТРАНСП используется только в формулах массивов, которые завершаются именно так. Если говорить кратко, формула массива — это формула, которая применяется сразу к нескольким ячейкам. Так как в шаге 1 вы выделили более одной ячейки, формула будет применена к нескольким ячейкам. Результат после нажатия клавиш CTRL+SHIFT+ВВОД будет выглядеть так:
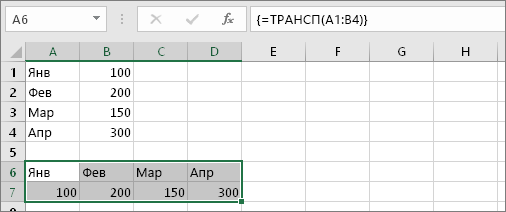
Советы
-
Вводить диапазон вручную не обязательно. Введя =ТРАНСП(, вы можете выделить диапазон с помощью мыши. Простой щелкните первую ячейку диапазона и перетащите указатель к последней. Но не забывайте: по завершении нужно нажать клавиши CTRL+SHIFT+ВВОД, а не просто клавишу ВВОД.
-
Нужно также перенести форматирование текста и ячеек? Вы можете копировать ячейки, вставить их и применить команду «Транспонировать». Но помните, что при этом образуются повторяющиеся данные. При изменении исходных ячеек их копии не обновляются.
-
Вы можете узнать больше о формулах массивов. Создайте формулу массива или ознакомьтесь с подробными рекомендациями и примерами.
Технические подробности
Функция ТРАНСП возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот. Функцию ТРАНСП необходимо вводить как формула массива в диапазон, содержащий столько же строк и столбцов, что и аргумент диапазон. Функция ТРАНСП используется для изменения ориентации массива или диапазона на листе с вертикальной на горизонтальную и наоборот.
Синтаксис
ТРАНСП(массив)
Аргументы функции ТРАНСП описаны ниже.
-
Массив. Обязательный аргумент. Массив (диапазон ячеек) на листе, который нужно транспонировать. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая — вторым столбцом и т. д. Если вы не знаете, как ввести формулу массива, см. статью «Создание формулы массива».
См. также
Транспонирование (поворот) данных из строк в столбцы и наоборот
Создание формулы массива
Поворот и выравнивание данных в ячейке
Использование формул массива: рекомендации и примеры
Нужна дополнительная помощь?
Содержание
- Процесс транспонирования
- Способ 1: оператор ТРАНСП
- Способ 2: транспонирование матрицы с помощью специальной вставки
- Вопросы и ответы
При работе с матрицами иногда нужно их транспонировать, то есть, говоря простыми словами, перевернуть. Конечно, можно перебить данные вручную, но Эксель предлагает несколько способов сделать это проще и быстрее. Давайте разберем их подробно.
Процесс транспонирования
Транспонирование матрицы – это процесс смены столбцов и строк местами. В программе Excel имеется две возможности проведения транспонирования: используя функцию ТРАНСП и при помощи инструмента специальной вставки. Рассмотрим каждый из этих вариантов более подробно.
Способ 1: оператор ТРАНСП
Функция ТРАНСП относится к категории операторов «Ссылки и массивы». Особенностью является то, что у неё, как и у других функций, работающих с массивами, результатом выдачи является не содержимое ячейки, а целый массив данных. Синтаксис функции довольно простой и выглядит следующим образом:
=ТРАНСП(массив)
То есть, единственным аргументом данного оператора является ссылка на массив, в нашем случае матрицу, который следует преобразовать.
Посмотрим, как эту функцию можно применить на примере с реальной матрицей.
- Выделяем незаполненную ячейку на листе, планируемую сделать крайней верхней левой ячейкой преобразованной матрицы. Далее жмем на значок «Вставить функцию», который расположен вблизи строки формул.
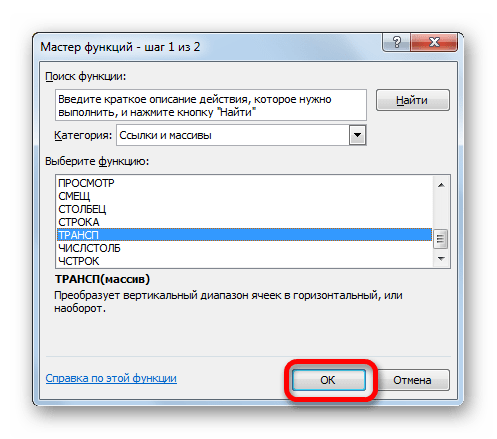
- Производится запуск Мастера функций. Открываем в нем категорию «Ссылки и массивы» или «Полный алфавитный перечень». После того, как отыскали наименование «ТРАНСП», производим его выделение и жмем на кнопку «OK».
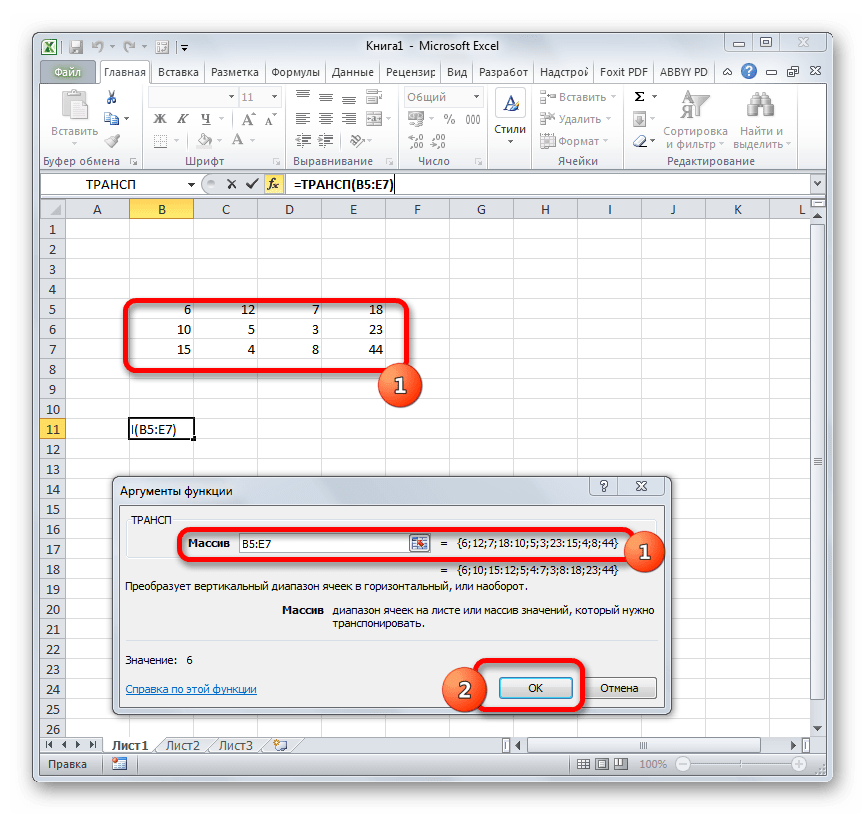
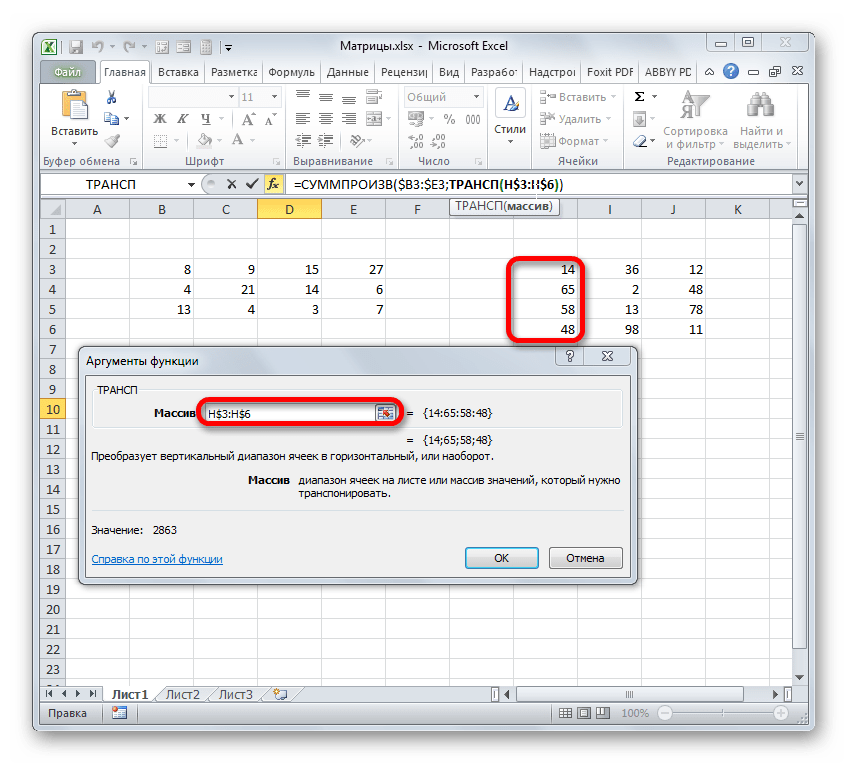
- Происходит запуск окна аргументов функции ТРАНСП. Единственному аргументу данного оператора соответствует поле «Массив». В него нужно внести координаты матрицы, которую следует перевернуть. Для этого устанавливаем курсор в поле и, зажав левую кнопку мыши, выделяем весь диапазон матрицы на листе. После того, как адрес области отобразился в окне аргументов, щелкаем по кнопке «OK».
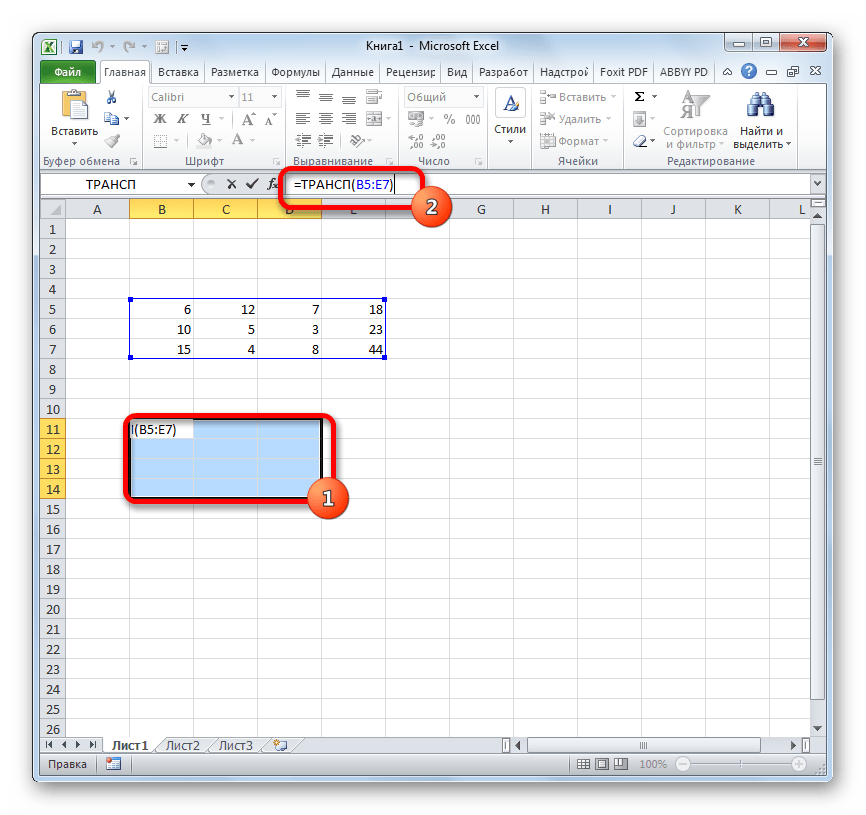
- Но, как видим, в ячейке, которая предназначена для вывода результата, отображается некорректное значение в виде ошибки «#ЗНАЧ!». Это связано с особенностями работы операторов массивов. Чтобы исправить эту ошибку, выделяем диапазон ячеек, в котором число строк должно быть равным количеству столбцов первоначальной матрицы, а число столбцов – количеству строк. Подобное соответствие очень важно для того, чтобы результат отобразился корректно. При этом, ячейка, в которой содержится выражение «#ЗНАЧ!» должна быть верхней левой ячейкой выделяемого массива и именно с неё следует начинать процедуру выделения, зажав левую кнопку мыши. После того, как вы провели выделение, установите курсор в строку формул сразу же после выражения оператора ТРАНСП, которое должно отобразиться в ней. После этого, чтобы произвести вычисление, нужно нажать не на кнопку Enter, как принято в обычных формулах, а набрать комбинацию Ctrl+Shift+Enter.
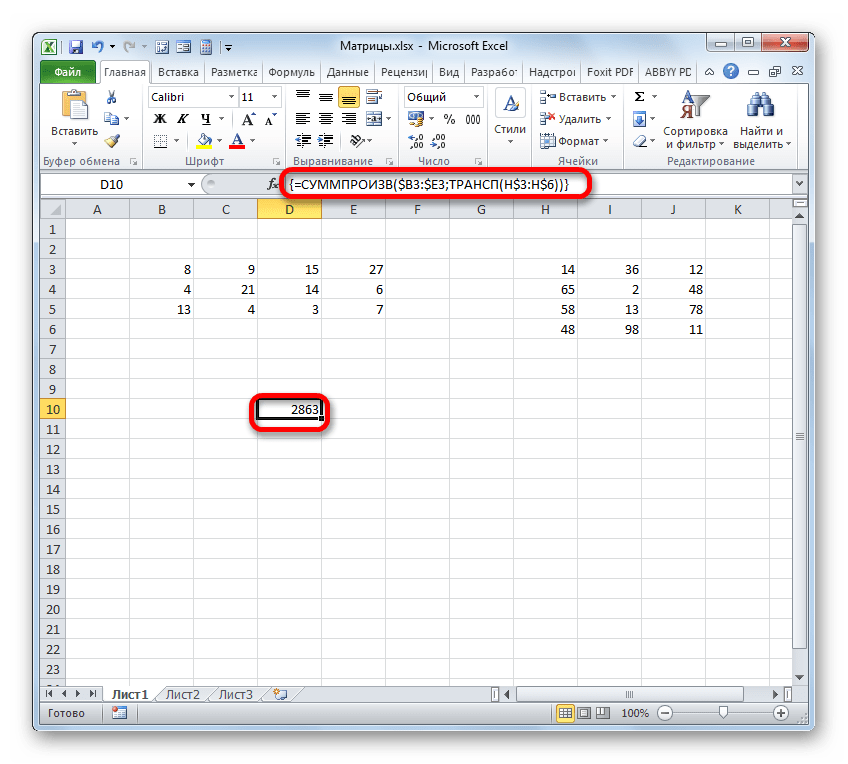
- После этих действий матрица отобразилась так, как нам надо, то есть, в транспонированном виде. Но существует ещё одна проблема. Дело в том, что теперь новая матрица представляет собой связанный формулой массив, который нельзя изменять. При попытке произвести любое изменение с содержимым матрицы будет выскакивать ошибка. Некоторых пользователей такое положение вещей вполне удовлетворяет, так как они не собираются производить изменения в массиве, а вот другим нужна матрица, с которой полноценно можно работать.
Чтобы решить данную проблему, выделяем весь транспонированный диапазон. Переместившись во вкладку «Главная» щелкаем по пиктограмме «Копировать», которая расположена на ленте в группе «Буфер обмена». Вместо указанного действия можно после выделения произвести набор стандартного сочетания клавиш для копирования Ctrl+C.
- Затем, не снимая выделения с транспонированного диапазона, производим клик по нему правой кнопкой мыши. В контекстном меню в группе «Параметры вставки» щелкаем по иконке «Значения», которая имеет вид пиктограммы с изображением чисел.
Вслед за этим формула массива ТРАНСП будет удалена, а в ячейках останутся только одни значения, с которыми можно работать так же, как и с исходной матрицей.
Урок: Мастер функций в Экселе
Способ 2: транспонирование матрицы с помощью специальной вставки
Кроме того, матрицу можно транспонировать с помощью одного элемента контекстного меню, который носит название «Специальная вставка».
- Выделяем исходную матрицу курсором, зажав левую кнопку мыши. Далее, перейдя во вкладку «Главная», щелкаем по пиктограмме «Копировать», размещенной в блоке настроек «Буфер обмена».
Вместо этого можно сделать и по-другому. Выделив область, кликаем по ней правой кнопкой мыши. Активируется контекстное меню, в котором следует выбрать пункт «Копировать».
В виде альтернативы двум предыдущим вариантам копирования, можно после выделения произвести набор комбинации горячих клавиш Ctrl+C.
- Выбираем на листе незаполненную ячейку, которая должна стать крайним верхним левым элементом транспонированной матрицы. Производим щелчок по ней правой кнопкой мыши. Вслед за этим активируется контекстное меню. В нем выполняем перемещение по пункту «Специальная вставка». Появляется ещё одно небольшое меню. В нем также имеется пункт под названием «Специальная вставка…». Кликаем по нему. Также можно, совершив выделение, вместо вызова контекстного меню набрать на клавиатуре комбинацию Ctrl+Alt+V.
- Активируется окно специальной вставки. Тут представлено много вариантов выбора, как именно можно вставить ранее скопированные данные. В нашем случае нужно оставить практически все настройки по умолчанию. Только около параметра «Транспонировать» следует установить галочку. Затем требуется нажать на кнопку «OK», которая размещена в нижней части данного окошка.
- После этих действий транспонированная матрица отобразится в заранее выбранной части листа. В отличие от предыдущего способа, мы уже получили полноценную матрицу, которую можно изменять, как и исходник. Никакой дальнейшей доработки или преобразований не требуется.
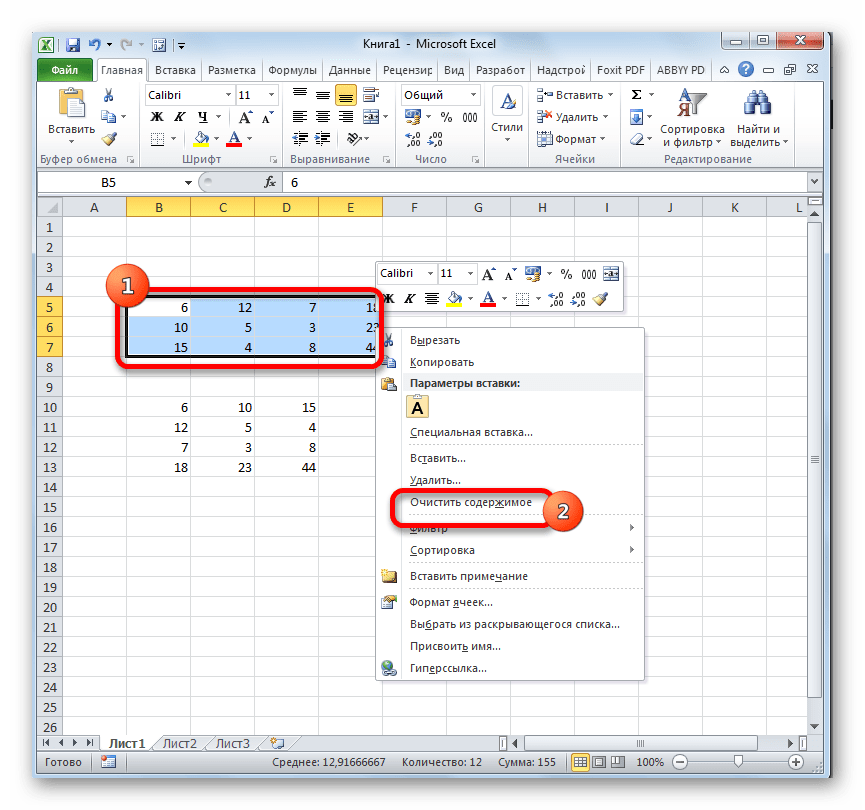
- Но при желании, если первоначальная матрица вам не нужна, её можно удалить. Для этого выделяем её курсором, зажав левую кнопку мыши. Затем выполняем щелчок по выделенному элементу правой кнопкой. В контекстном меню, которое откроется вслед за этим, выбираем пункт «Очистить содержимое».
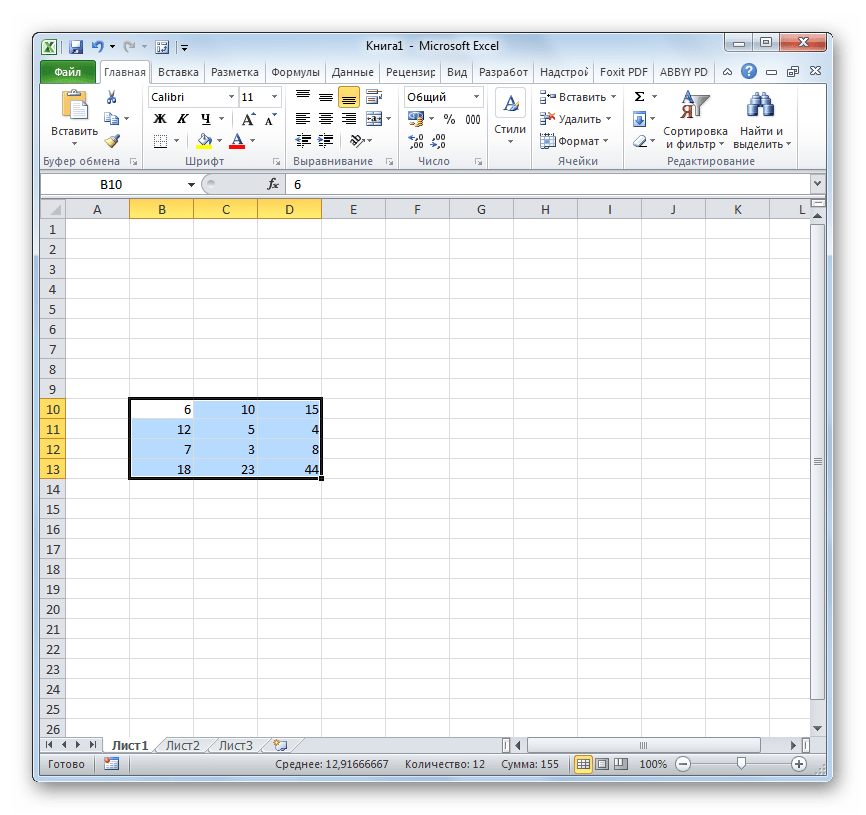
После указанных действий на листе останется только преобразованная матрица.
Этими же двумя способами, о которых шла речь выше, можно транспонировать в Excel не только матрицы, но и полноценные таблицы. Процедура при этом будет практически идентичной.
Урок: Как перевернуть таблицу в Экселе
Итак, мы выяснили, что в программе Excel матрицу можно транспонировать, то есть, перевернуть, поменяв столбцы и строчки местами, двумя способами. Первый вариант предполагает использование функции ТРАНСП, а второй – инструменты специальной вставки. По большому счету конечный результат, который получается при использовании обоих этих способов, ничем не отличается. Оба метода работают практически в любой ситуации. Так что при выборе варианта преобразования, на первый план выходят личные предпочтения конкретного пользователя. То есть, какой из данных способов для вас лично удобнее, тот и используйте.
Еще статьи по данной теме:
Помогла ли Вам статья?
Понятие «транспонировать» почти не встречается в работе пользователей ПК. Но тем, кто работает с массивами, будь то матрицы в высшей математике или таблицы в Excel, приходится сталкиваться с этим явлением.
Транспонированием таблицы в Excel называется замена столбцов строками и наоборот. Иными словами – это поворот в двух плоскостях: горизонтальной и вертикальной. Транспонировать таблицы можно тремя способами.
Способ 1. Специальная вставка
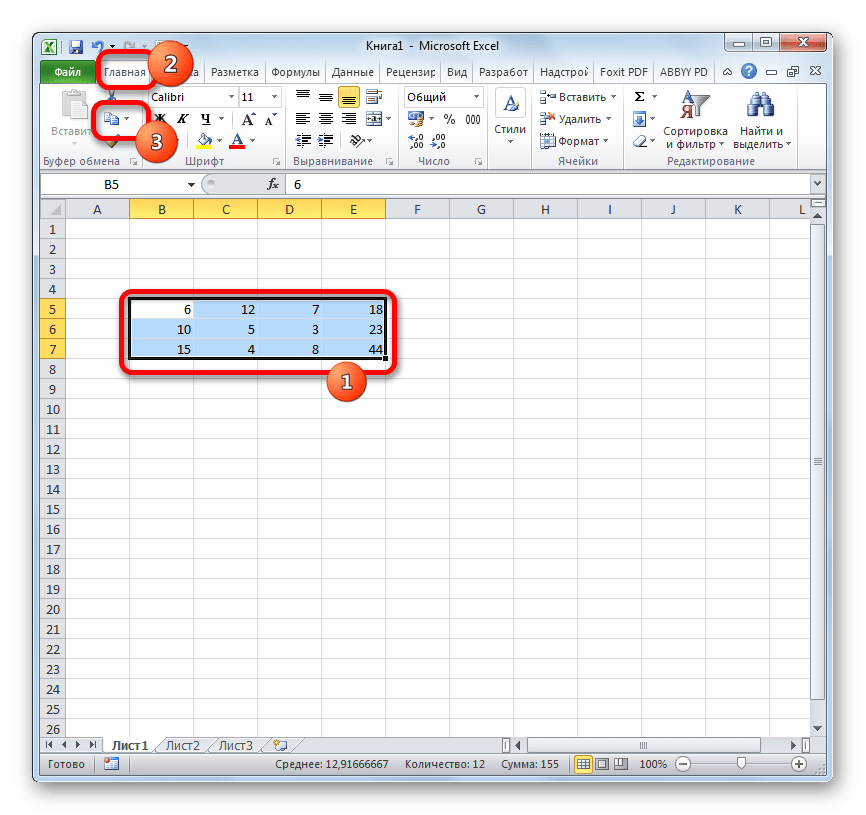
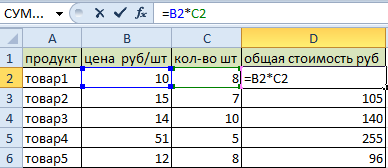
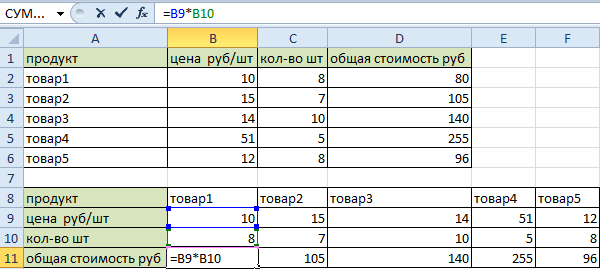
Самый простой и универсальный путь. Рассмотрим сразу на примере. Имеем таблицу с ценой некоего товара за штуку и определенным его количеством. Шапка таблицы расположена горизонтально, а данные расположены вертикально соответственно. Стоимость рассчитана по формуле: цена*количество. Для наглядности примера подсветим шапку таблицы зеленым цветом.
Нам нужно расположить данные таблицы горизонтально относительно вертикального расположения ее шапки.
Чтобы транспонировать таблицу, будем использовать команду СПЕЦИАЛЬНАЯ ВСТАВКА. Действуем по шагам:
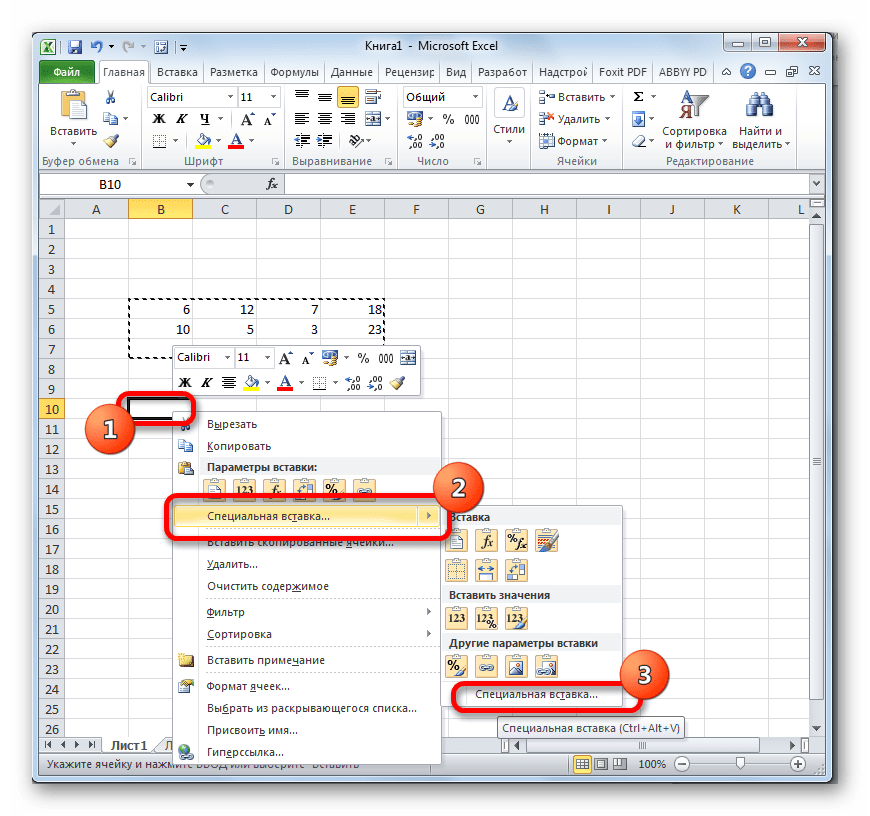
- Выделяем всю таблицу и копируем ее (CTRL+C).
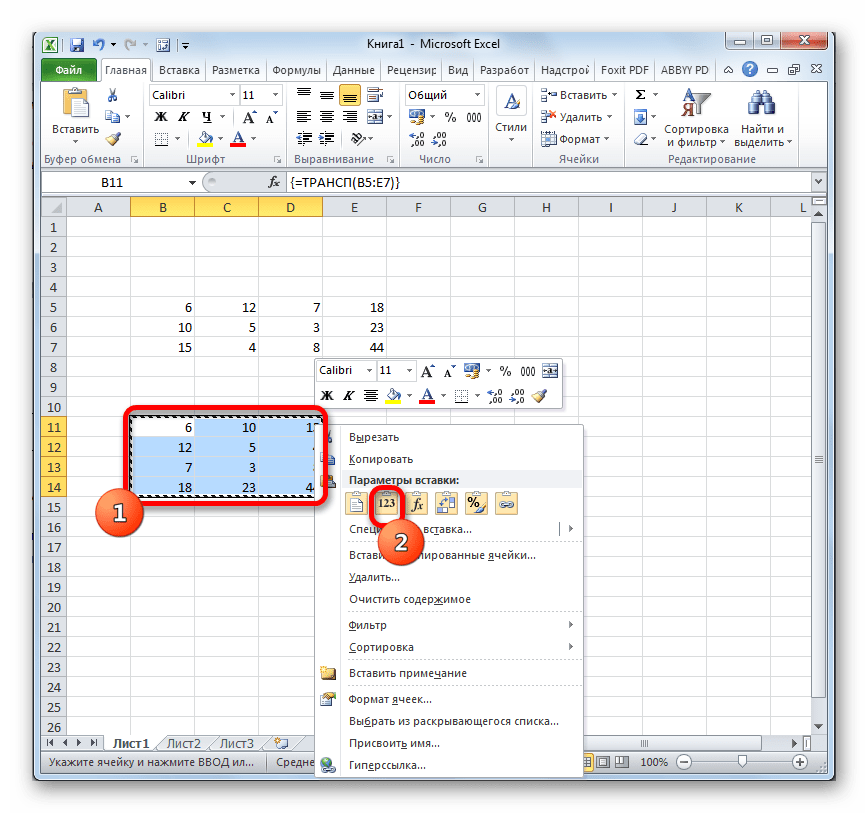
- Ставим курсор в любом месте листа Excel и правой кнопкой вызываем меню.
- Кликаем по команде СПЕЦИАЛЬНАЯ ВСТАВКА.
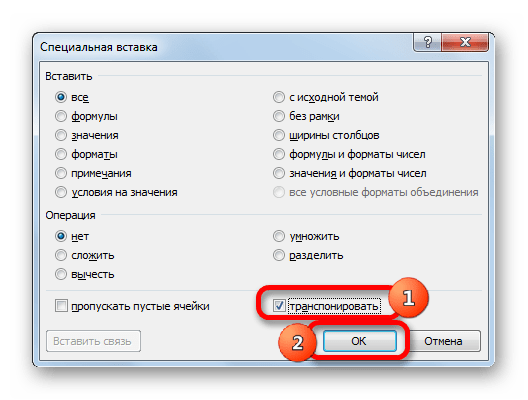
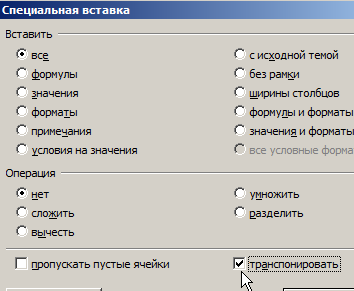
- В появившемся окне ставим галочку возле пункта ТРАНСПОНИРОВАТЬ. Остальное оставляем как есть и жмем ОК.
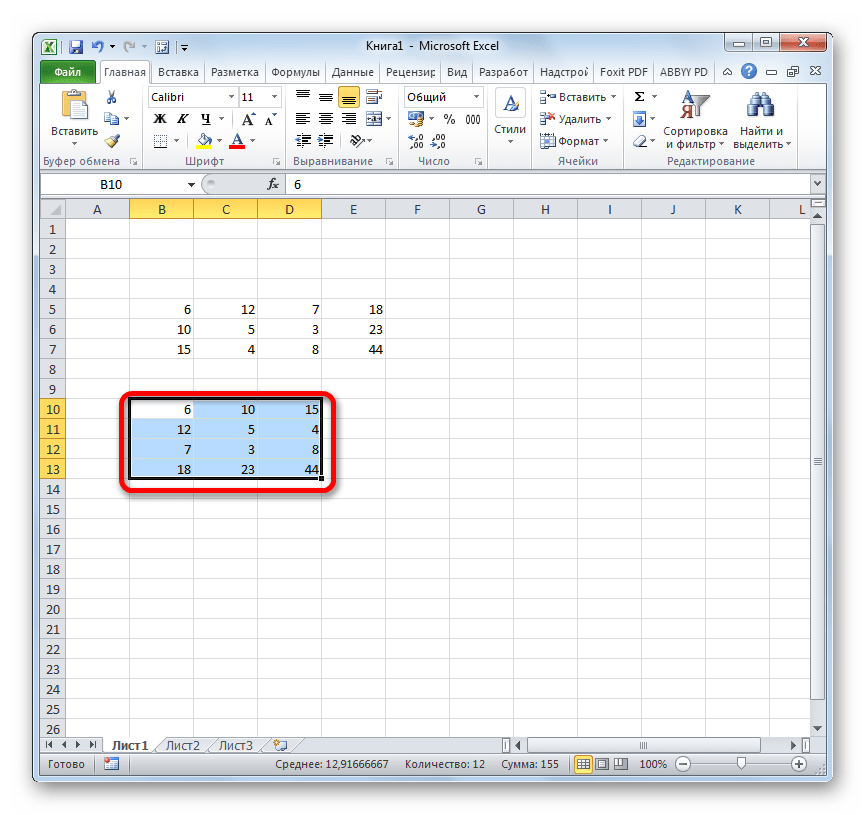
В результате получили ту же таблицу, но с другим расположением строк и столбцов. Причем, заметим, что зеленым подсвечены ячейки с тем же содержанием. Формула стоимости тоже скопировалась и посчитала произведение цены и количества, но уже с учетом других ячеек. Теперь шапка таблицы расположена вертикально (что хорошо видно благодаря зеленому цвету шапки), а данные соответственно расположились горизонтально.
Аналогично можно транспонировать только значения, без наименований строк и столбцов. Для этого нужно выделить только массив со значениями и проделать те же действия с командой СПЕЦИАЛЬНАЯ ВСТАВКА.
Способ 2. Функция ТРАНСП в Excel
С появлением СПЕЦИАЛЬНОЙ ВСТАВКИ транспонирование таблицы при помощи команды ТРАНСП почти не используется по причине сложности и большего времени на операцию. Но функция ТРАНСП все же присутствует в Excel, поэтому научимся ею пользоваться.
Снова действует по этапам:
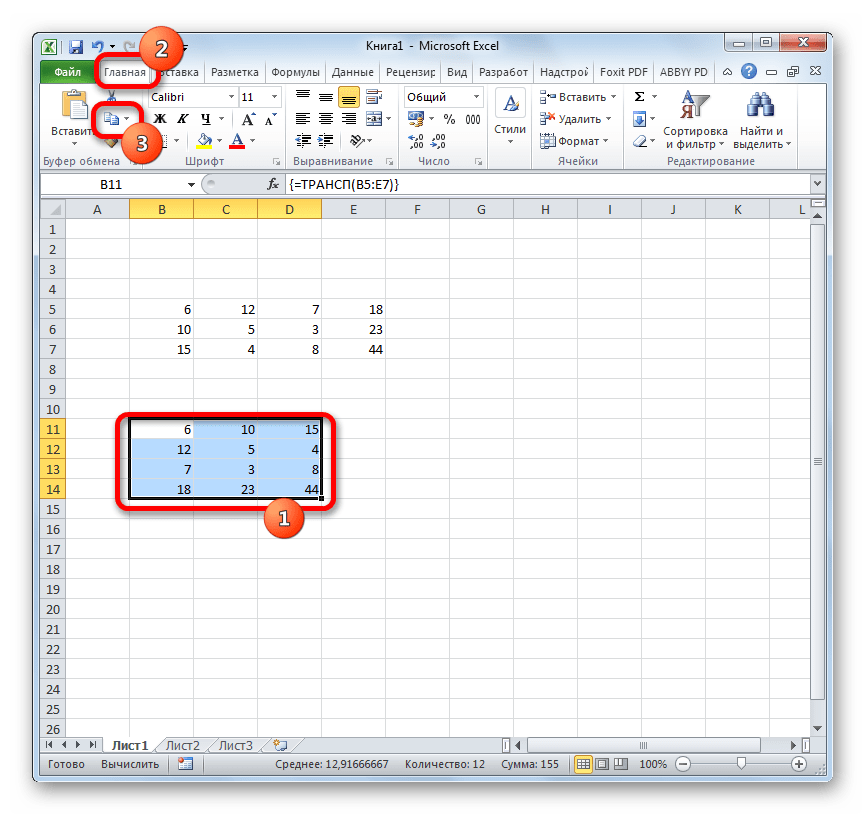
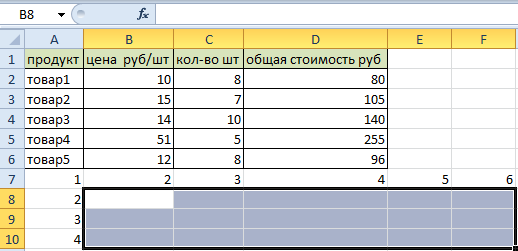
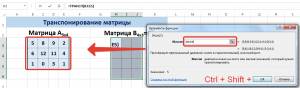
- Правильно выделяем диапазон для транспонирования таблицы. В данном примере исходной таблицы имеется 4 столбца и 6 строк. Соответственно мы должны выделить диапазон ячеек в котором будет 6 столбцов и 4 строки. Как показано на рисунке:
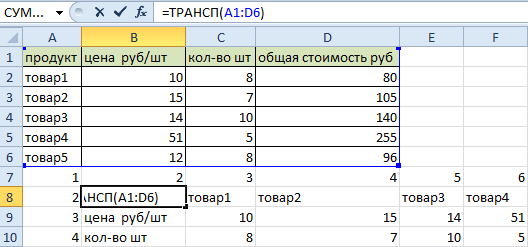
- Сразу заполняем активную ячейку так чтобы не снять выделенную область. Вводим следующую формулу:=ТРАНСП(A1:D6)
- Нажимаем CTRL+SHIFT+ENTER. Внимание! Функия ТРАНСП()работает тилько в массиве. Поэтому после ее ввода нужно обязательно нажать комбинацию горячих клавиш CTRL+SHIFT+ENTER для выполнения функции в массиве, а не просто ENTER.
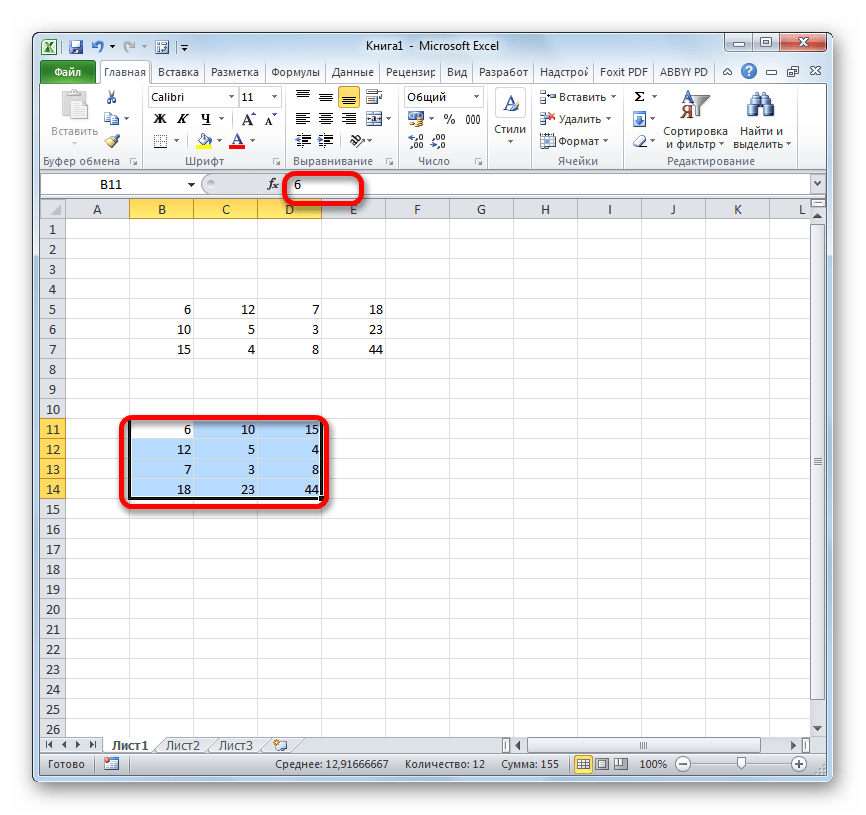
Обратите внимание, что формула не скопировалась. При нажатии на каждую ячейку становится видно, что эта таблица была транспонирована. К тому же все исходное форматирование утеряно. Придется выравнивать и подсвечивать снова. Так же стоит обратить внимание на то что транспонированная таблица привязанная к исходной. Измененные значения исходной таблице автоматически обновляются в транспонированной.
Способ 3. Сводная таблица
Те, кто тесно работает с Excel, знают, что сводная таблица многофункциональна. И одной из ее функций является возможность транспонирования. Правда, оно будет выглядеть немного иначе, чем в предыдущих примерах.
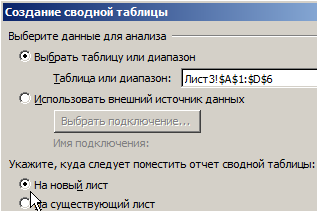
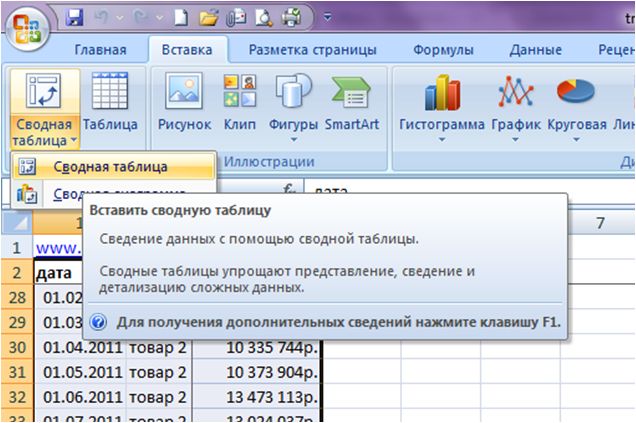
- Создадим сводную таблицу. Для этого выделим исходную таблицу и откроем пункт ВСТАВКА – СВОДНАЯ ТАБЛИЦА.
- Местом, где будет создана сводная таблица, выбираем новый лист.
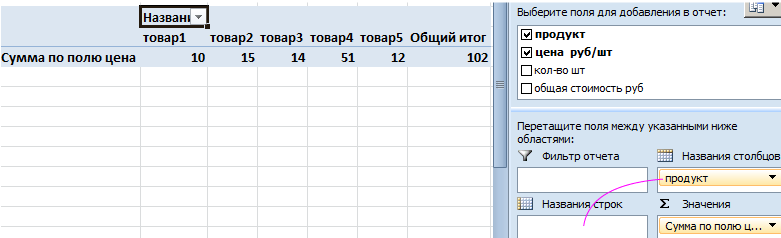
- В получившемся макете сводных таблиц можем выбрать необходимые пункты и перенести их в нужные поля. Перенесем «продукт» в НАЗВАНИЯ СТОЛБЦОВ, а «цена за шт» в ЗНАЧЕНИЯ.
- Получили сводную таблицу по нужному нам полю. Также команда автоматически подсчитала общий итог.
- Можно убрать галочку у ЦЕНА ЗА ШТ и поставить галочку рядом с ОБЩАЯ СТОИМОСТЬ. И тогда получим сводную таблицу по стоимости товаров, а также опять общий итог.
Скачать примеры транспонирования таблиц в Excel.
Это достаточно своеобразный способ частичного транспонирования, позволяющий заменить столбцы на строки (наоборот – не получится) и дополнительно узнать общую сумму по заданному полю.
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
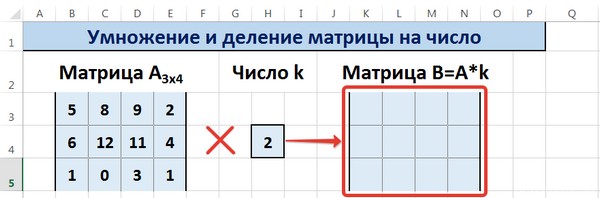
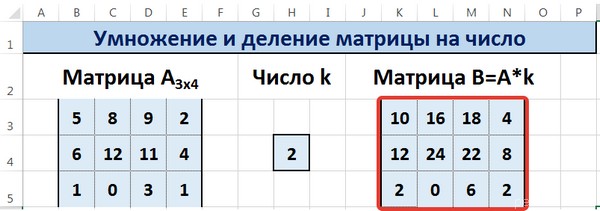
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
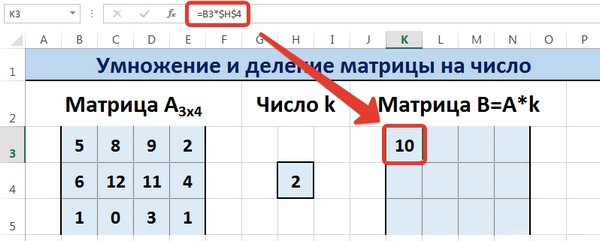
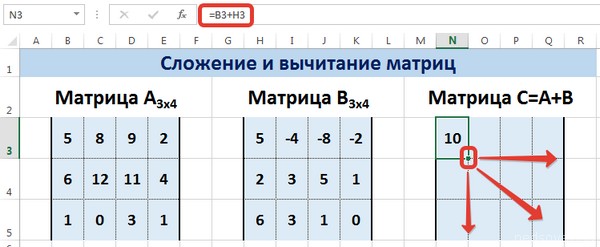
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
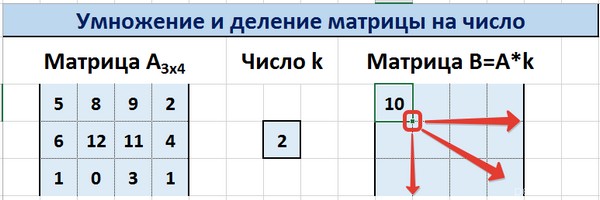
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
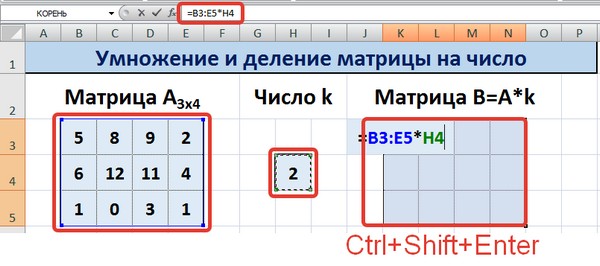
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
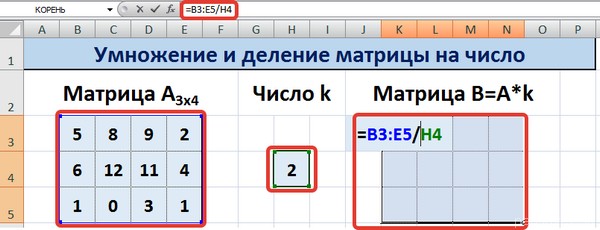
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
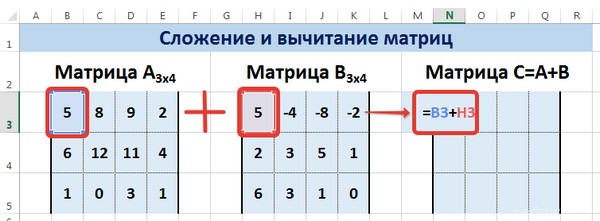
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
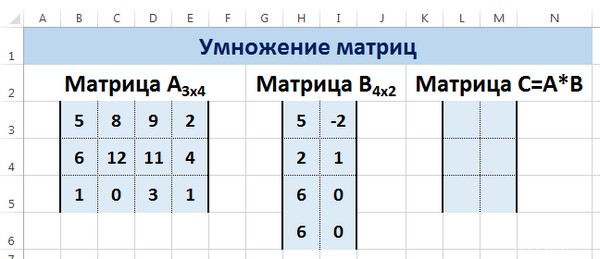
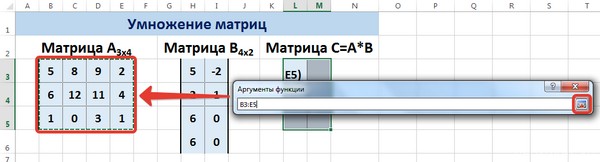
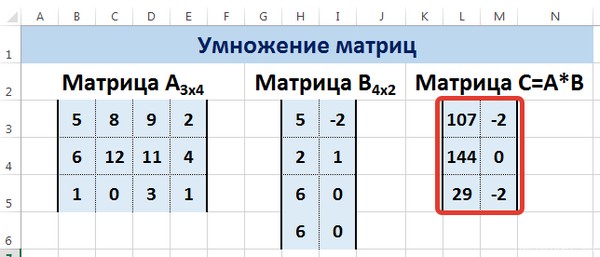
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
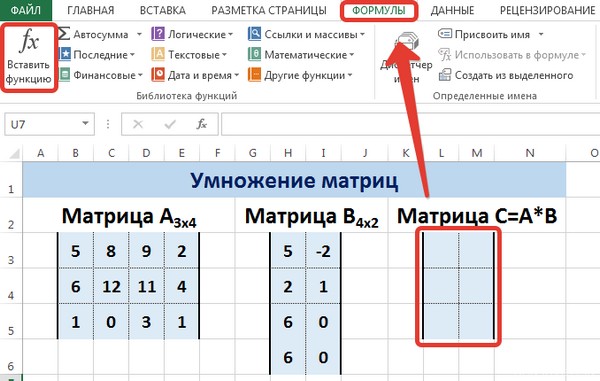
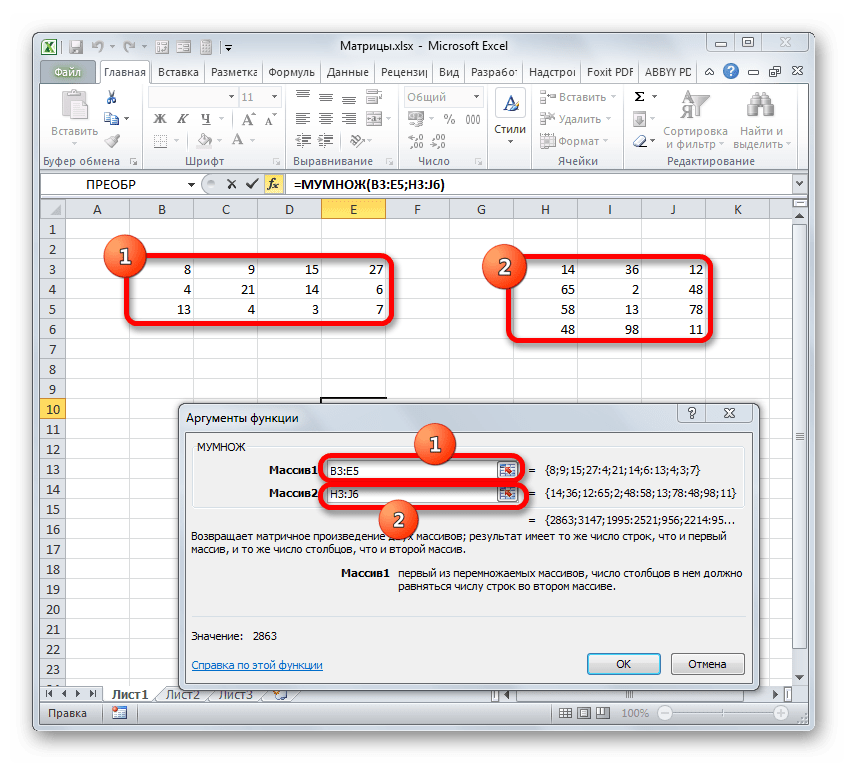
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
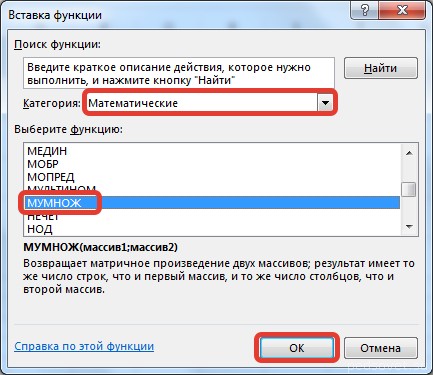
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
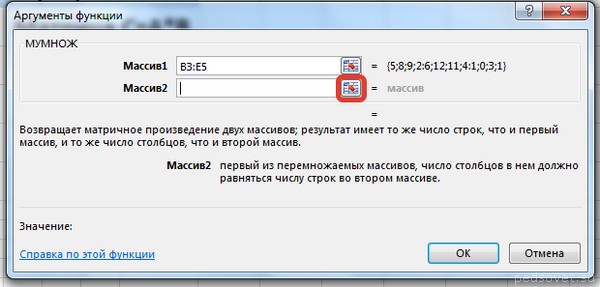
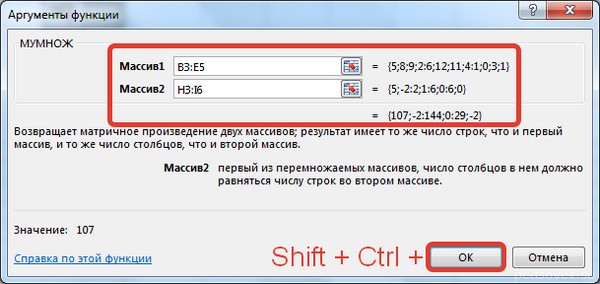
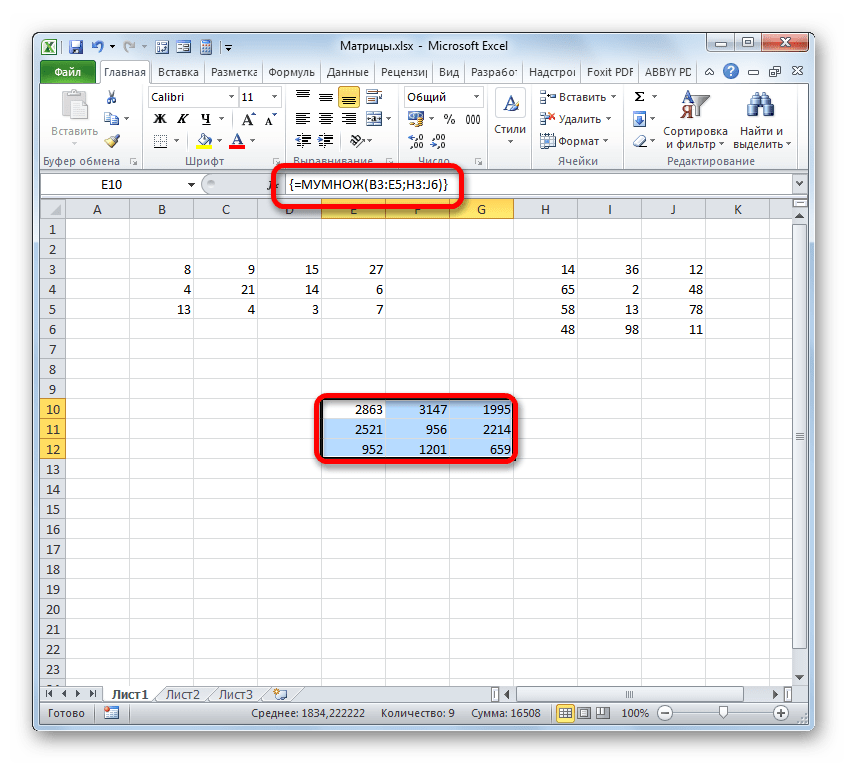
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
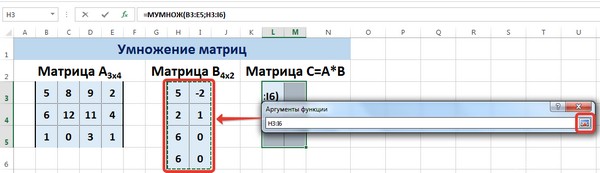
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
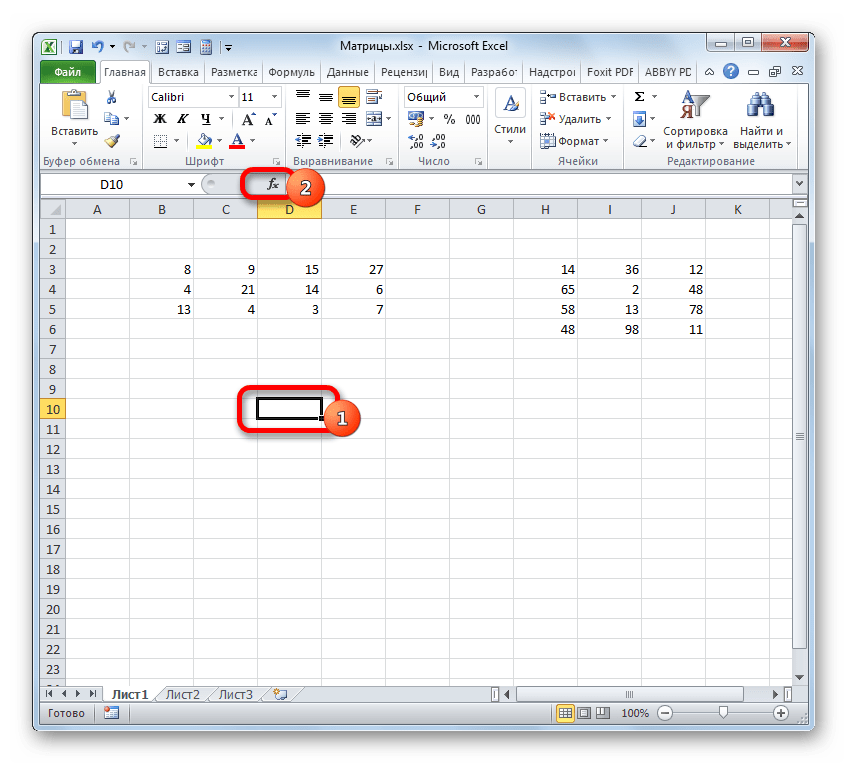
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
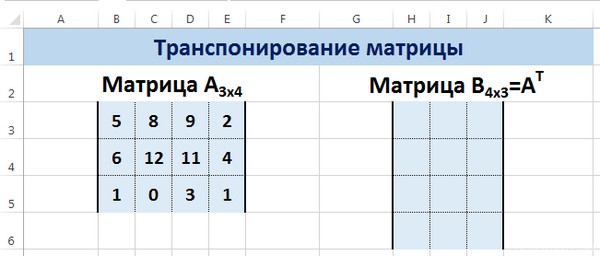
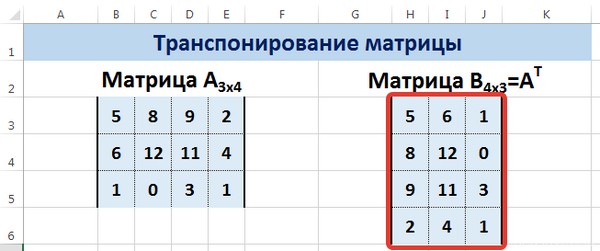
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
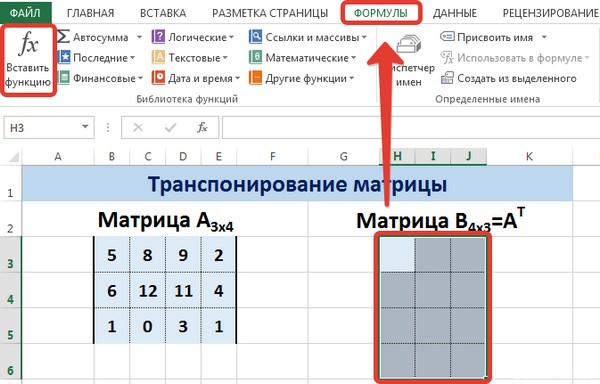
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
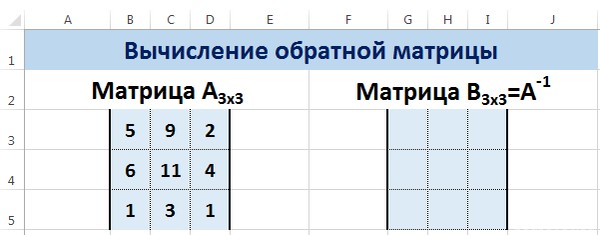
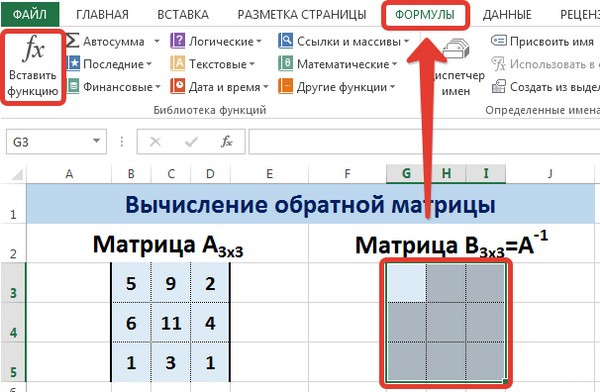
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
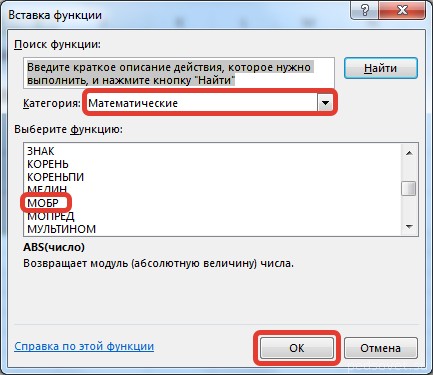
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
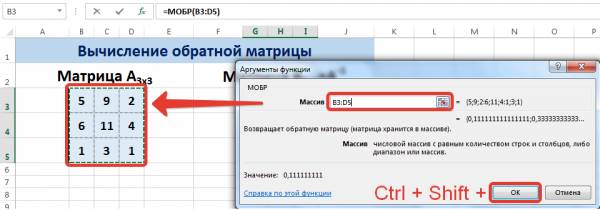
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
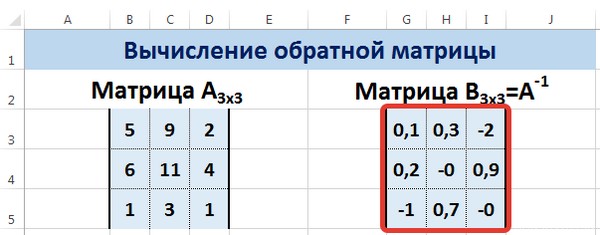
Нажмите для увеличения
Мы получили обратную матрицу.
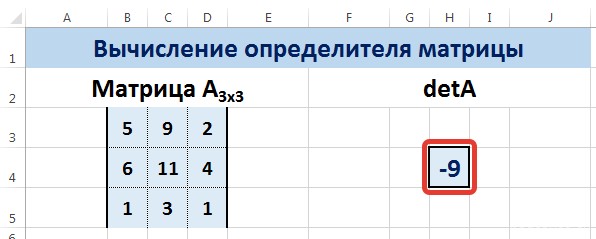
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
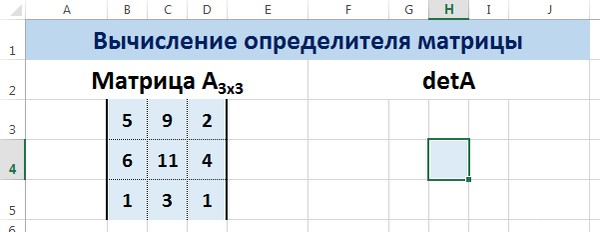
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
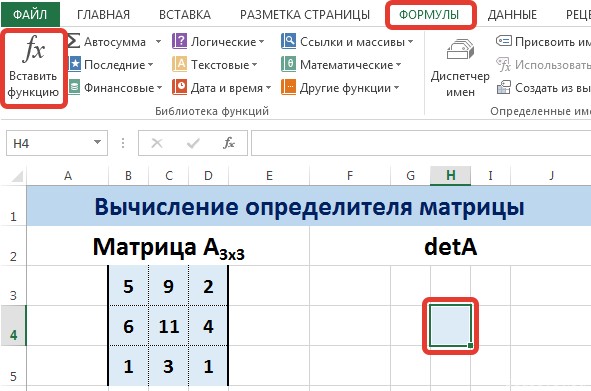
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
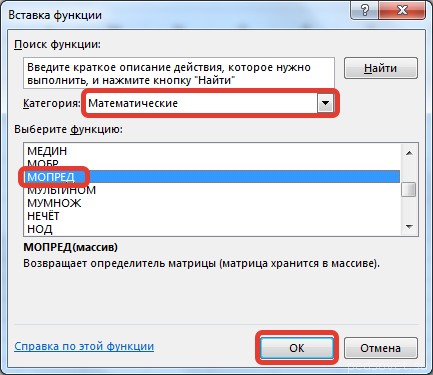
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
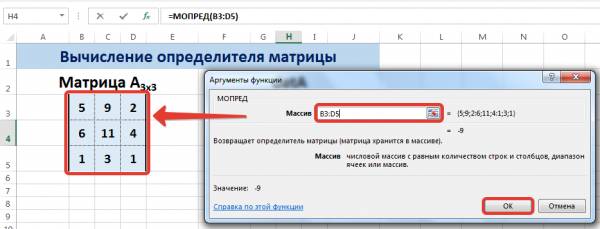
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
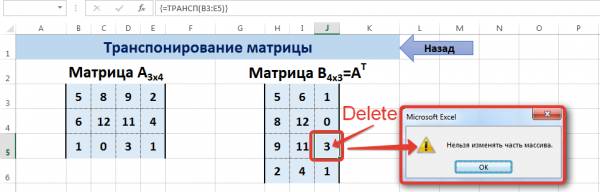
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Векторы и матрицы в Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Векторы и матрицы в Excel
C овокупность n чисел 
Два n -мерных вектора 


Суммой двух n -мерных векторов 

Операция сложения векторов обладает свойствами коммутативности 

Вектор 
Вектор 

Операция вычитания векторов определяется как сложение с противоположным вектором 
Под произведением вектора 

Умножение вектора на число обладает свойством ассоциативности 

Модуль (норма, длина) вектора 
Пример вычисления модуля вектора 
Р
исунок 1 – Вычисление длины вектора
Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.
В общем случае скалярное произведение двух векторов 




Операция скалярного умножения векторов обладает следующими свойствами:

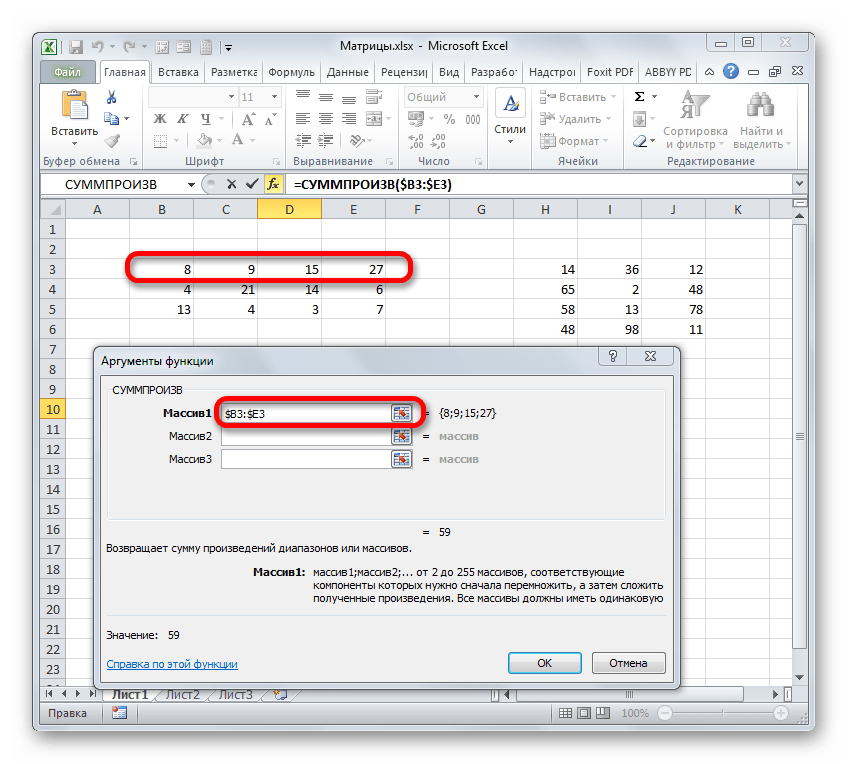
В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).
Векторным произведением вектора 







Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.
Р
исунок 2 – Определение скалярного произведения двух векторов
Значение векторного произведения определяется следующим образом:
На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов 
Р
исунок 4 – Вычисление векторного произведения векторов
Перейдем к рассмотрению основных операций матричного исчисления.
Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :
Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:
Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.
Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается
При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы 
Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:
Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:
Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица
называемая транспонированной по отношению к матрице А.
Если А=А Т , то такая матрица называется симметричной.
В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.
Р
исунок 5 – Вызов функции ТРАНСП
Пример. Имеем исходную матрицу

Из определения ясно, что транспонированной будет матрица А Т :

Решение задачи в Excel представлено на рисунке 6
Рисунок 6 – Транспонирование матрицы
Порядок решения следующий:
— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);
— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);
— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;
— нажать Shit + Ctrl + Enter .
Суммой матриц А


Произведение матрицы на число — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:
Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы 





В Excel для вычисления произведения матриц используется функция
= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).
Р
исунок 7 – Умножение матриц
Формула для расчета произведения матриц должна быть введена как формула массива!
Пусть даны матрицы
Вычислим их произведение в Excel (рисунок 8).
— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);
— 
—
шаг 3 – выделить результирующий массив и нажать F2;
—
шаг 3 – нажать Shift+Ctrl+Enter.
Рисунок 8 – Вычисление произведения матриц
Действие умножения матрицы на матрицу обладает свойствами:
Отметим, что в общем случае
Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.
При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).
Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.
Для матрицы 2х2 определитель вычисляется как
Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:



Возможно разложение как по строкам, так и по столбцам.
В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).
Рисунок 9 – Расчет определителя матрицы
Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .
Детерминант треугольной матрицы равен произведению ее диагональных элементов
Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E
Обратную матрицу можно найти по следующей формуле:



Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).
Рисунок 10 – Расчет обратной матрицы
Заметим, что функция применяется к массиву как в ранее приведенных примерах.
Проверим выполнение условия А А -1 = E (рисунок 11)
Р
исунок 11- Произведение матрицы на обратную матрицу
Собственным числом квадратной матрицы
называется такое число 

Или, по-другому, собственными числами матрицы А являются корни уравнения 
Матрица 


Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:
Необходимо найти такие значения , при котором
Оформим лист Excel следующим образом (рисунок 12):
Рисунок 12 – Вычисление собственного числа матрицы
В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.
Из рисунка 12 видно, что при =0 определитель также равен 0, т.е. =0 есть первое собственное число матрицы.
Д
ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения , отображаемом в ячейке $F$2.
Рисунок 13 – Вычисление собственного числа матрицы
О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).
Рисунок 14 – Результат поиска решения
Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат =0.
П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):
Рисунок 15 – Ввод ограничения
В результате поиска получаем второе значение собственного числа: =3.
Повторим поиск при ограничении.
Если установить в ограничениях >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях
П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)
Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении
Рисунок 17 — Результат поиска третьего собственного числа
Собственным вектором соответствующим собственному числу λ называют такой вектор 
Найдем собственный вектор матрицы
Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.
1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).
2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.
3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.
4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор 
5. В ячейки (H2:H4) заносим умножение столбца 
6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).
7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.
Нажать кнопку « Выполнить ».
В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).
Рисунок 18 – Определение собственного вектора матрицы
Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.
Задания для самостоятельной работы
Повторить решение всех примеров, приведенных в Лекции №5.
Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15
Определить длину векторов.
Вычислить сумму и разность векторов.
Определить скалярное произведение этих векторов.
Определить угол между векторами.
Определить векторное произведение двух векторов.
Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.
Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.
Получить транспонированные матрицы исходных матриц.
Проверить правильность решения путем умножения исходной матрицы на транспонированную.
Определить произведение исходных матриц.
Найти матрицу 3-го порядка для исходной квадратной матрицы.
Определить детерминант исходной квадратной матрицы.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
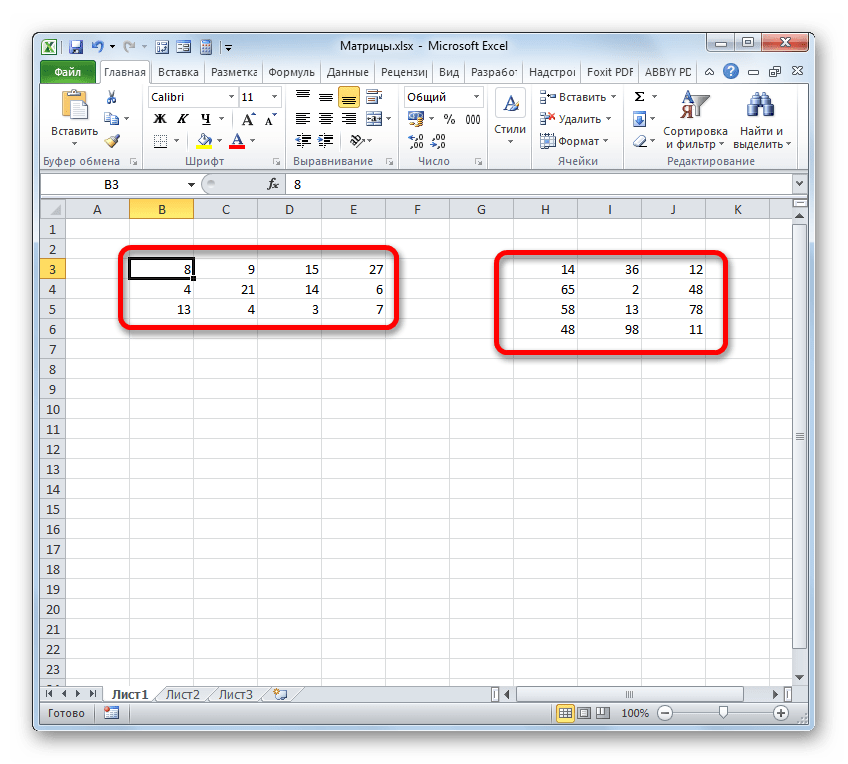
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
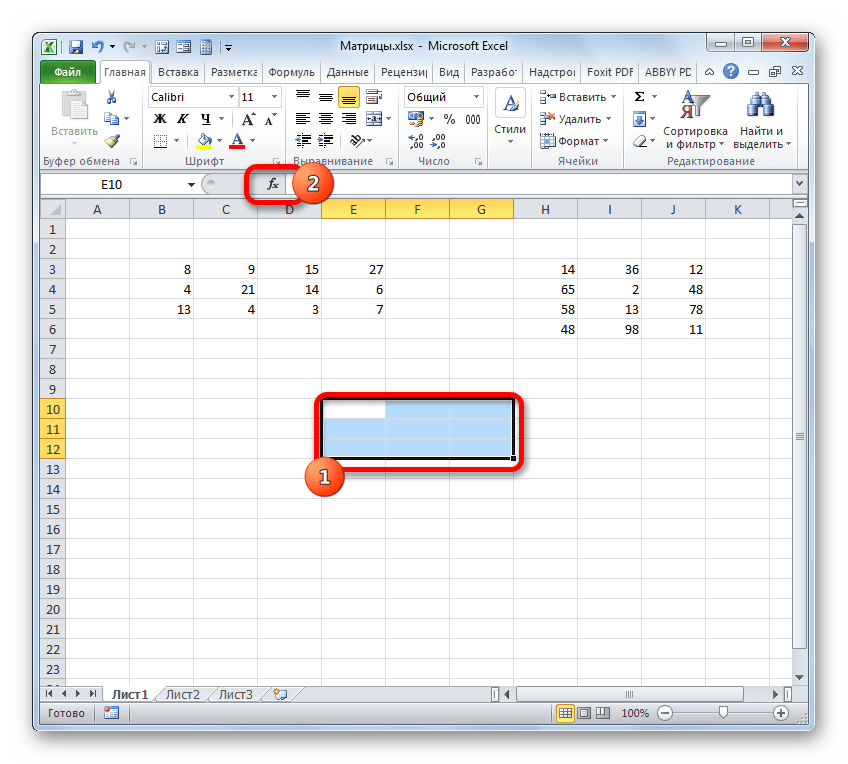
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
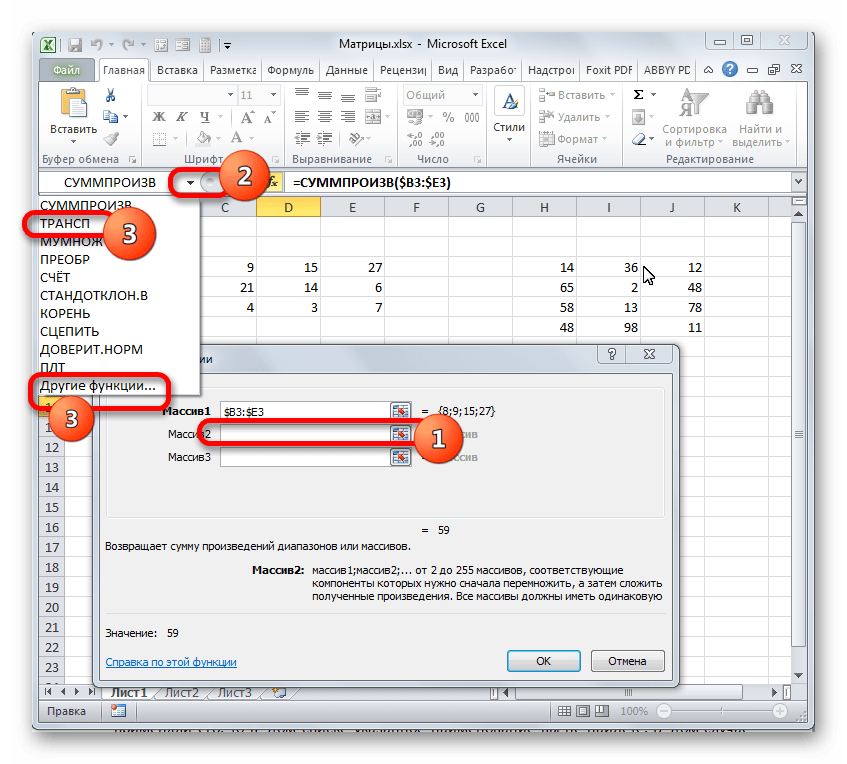
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
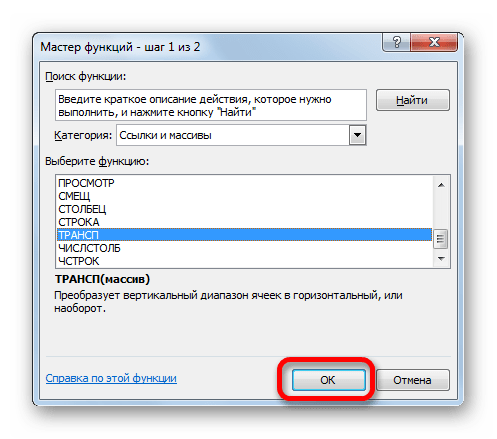
Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
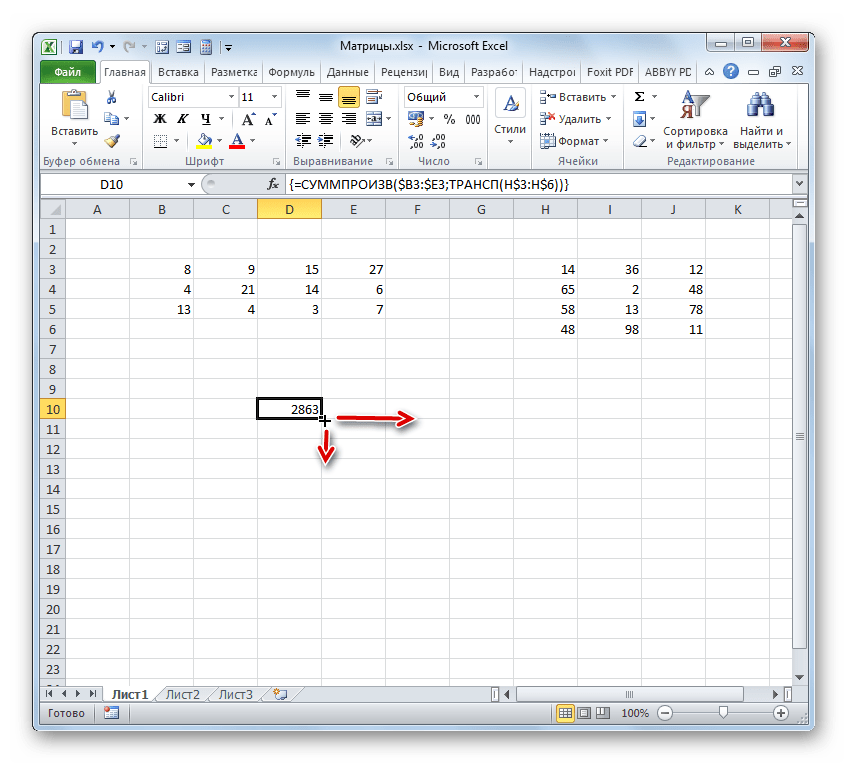
Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
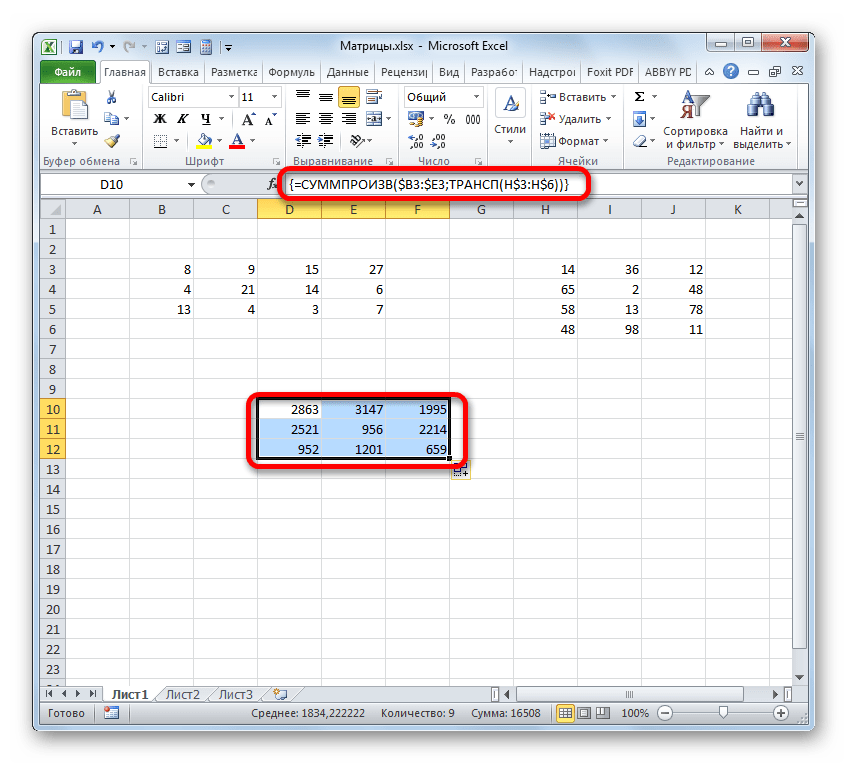
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Помимо этой статьи, на сайте еще 12604 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
источники:
http://infourok.ru/vektori-i-matrici-v-ecel-1119397.html
http://lumpics.ru/how-to-multiply-matrices-in-excel/
Транспонировать данные в Excel можно с помощью:
- «Специальной» вставки с галочкой «Транспонировать»;
- Функции Excel =трансп();
- и с помощью сводной таблицы.
Рассмотрим данные способы транспонирования на примерах.
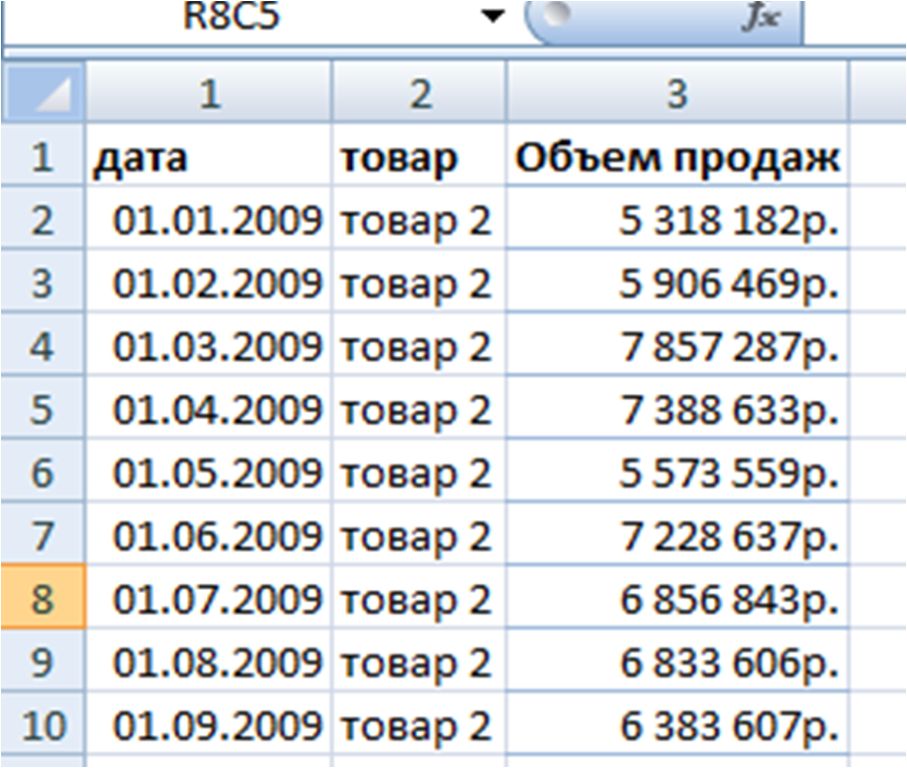
У нас есть таблица с данными, и мы хотим из табличного представления данных сделать строчное — для этого транспонируем данные.
1-ый способ транспонирования — специальная вставка
Транспонируем данные с помощью специальной вставки с галочкой «транспонировать».
Для этого выделяем необходимые данные и копируем их с помощью кнопки «копировать» или с помощью сочетания клавиш ctrl+c.
Затем переходим на новый лист, устанавливаем курсор, куда хотим вставить данные, и заходим в «специальную вставку»: нажимаем кнопку в меню «Специальная вставка» или нажимаем правой кнопкой мыши и выбираем пункт «Специальная вставка».
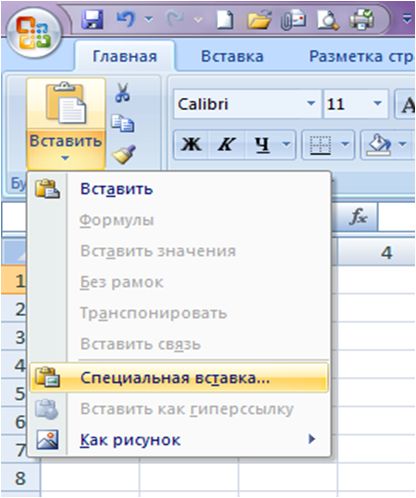
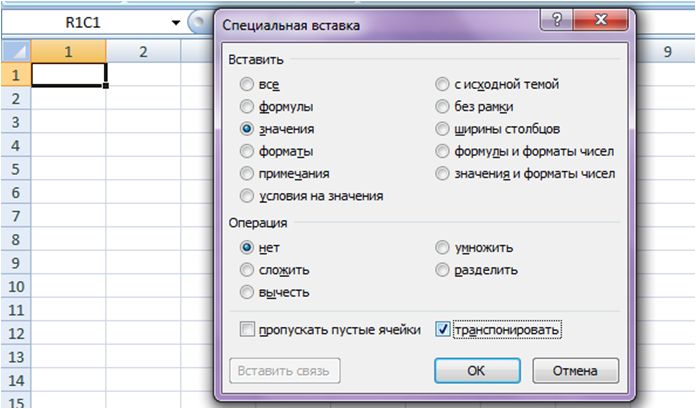
После нажатия откроется диалоговое окно, в котором ставим галочку «транспонировать» и нажимаем ОК
Данные переворачиваются, и мы получаем нужное нам строчное представление:
Обратите внимание, что при таком способе транспонирования данных связь между исходными данными и перевернутыми отсутствует. Т.е. если мы меняем исходные данные, данные в транспонированной таблице не меняются. Как транспонировать данные с сохранением связи с исходником?
2-ой способ транспонирования функция Excel =ТРАНСП()
Рассмотрим второй способ транспонирования, который, в отличие от первого, позволяет сохранить связь с исходными данными, — с помощью функции Excel «=ТРАНСП()»
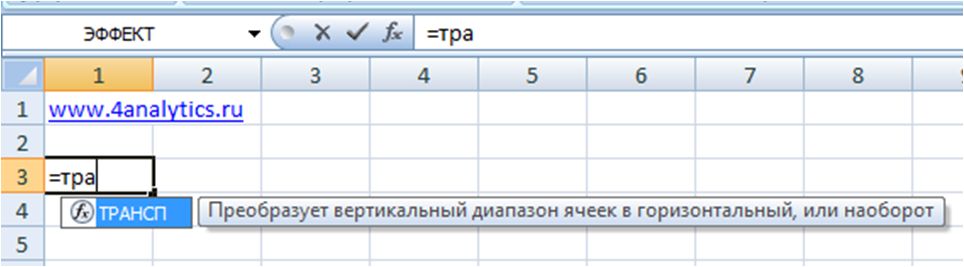
Итак, как с помощью формулы =ТРАНСП перевернуть данные?
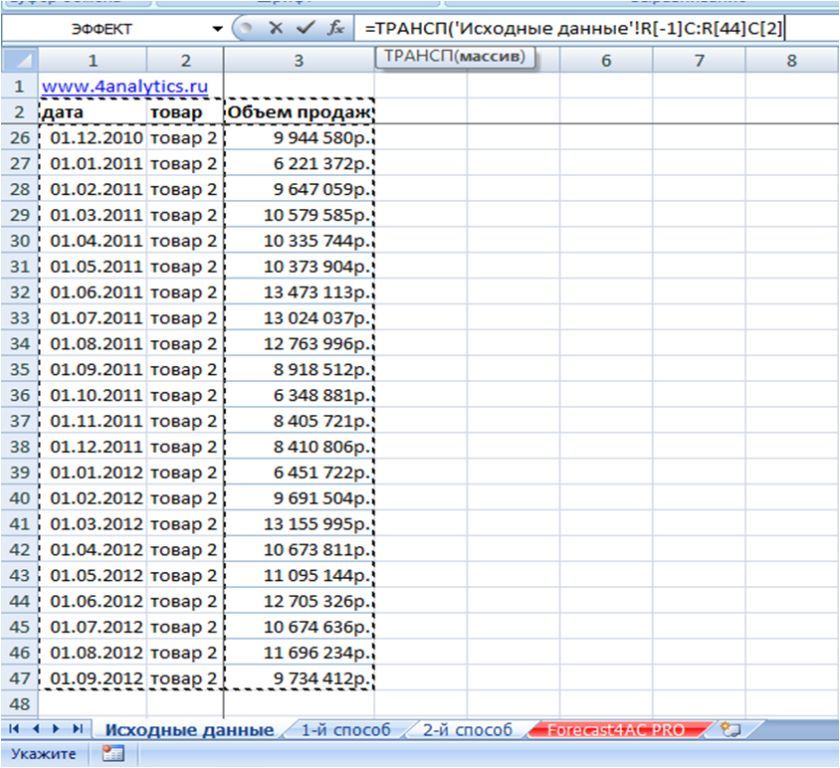
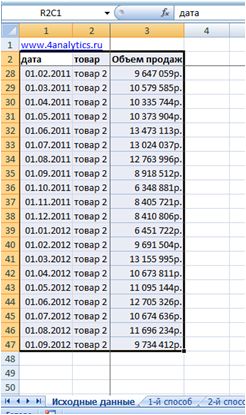
1. Вводим формулу (как в картинке выше) и передаем в неё ссылку на весь диапазон, который хотим перевернуть:
2. Выделяем диапазон в листе с формулой =ТРАНСП, равный массиву исходных данных (т.е равное количество строк и столбцов в перевернутом виде).
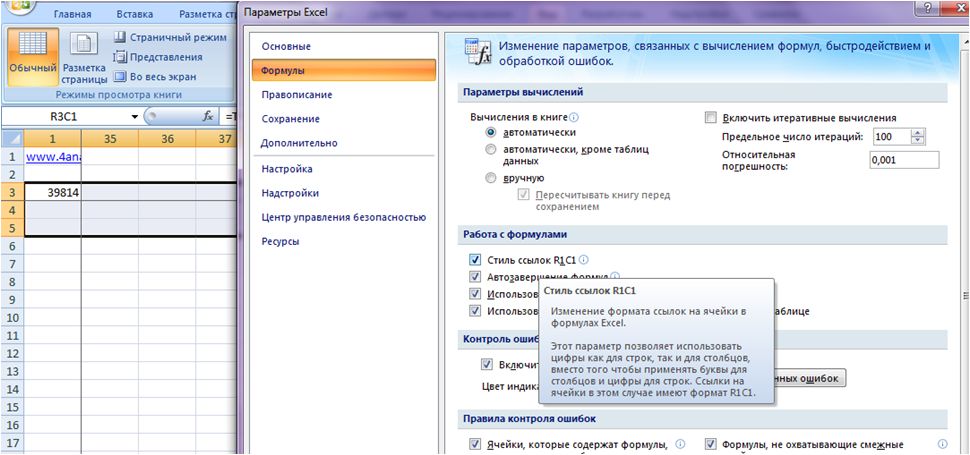
Чтобы легче было выделить массив нужного размера, рекомендую перевести стиль ссылок в вид R1C1, чтобы столбцы и строки стали номерами. Это делается в параметрах Excel -> в разделе «Формулы» -> поставить галочку «Стиль ссылок R1C1».
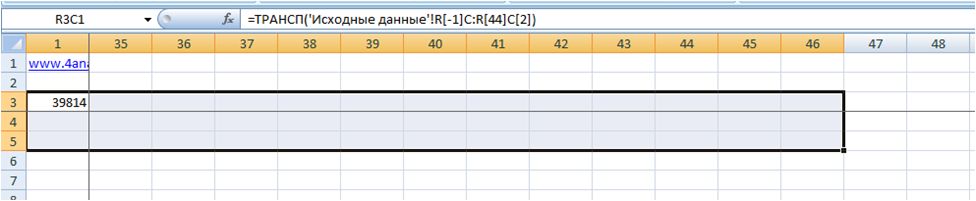
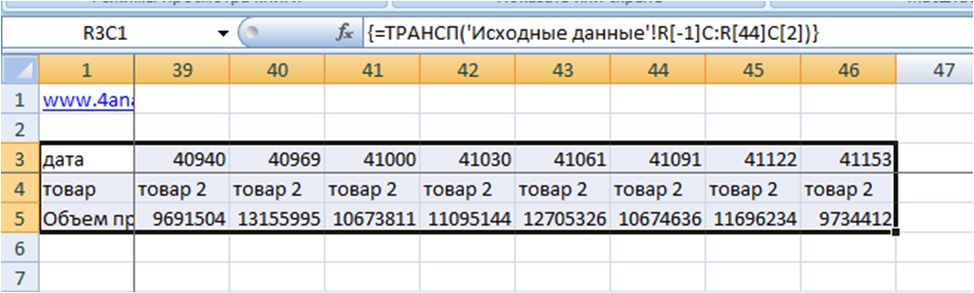
Например, у нас в исходных данных значения расположены со 2й по 47 строку и 3 столбца, в источнике данных мы выделим 3 строки и 46 столбцов начиная с 1-го. После того, как диапазон выделен, нажимаем на клавиатуре клавишу F2, а затем одновременно Ctrl+Shift+Enter, таким образом мы вводим формулу массива и получаем перевернутые данные с сохраненными ссылками на первоначальный диапазон.
Скачать пример транспонирования в Excel
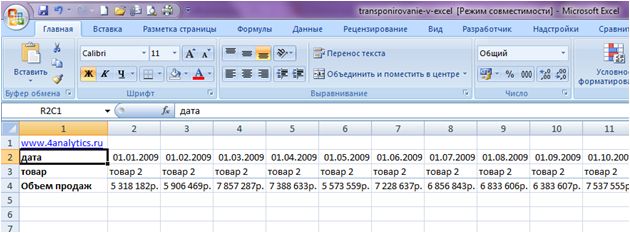
Теперь дату преобразуем в формат «Дата», а продажи в «руб». В итоге получаем диапазон, аналогичный исходным данным, только с перевернутыми значениями и, что важно, связанный с исходными данными. Если мы будем изменять исходные данные, то автоматически они будут меняться на листе с транспонированными данными.
Аналогичным образом диапазон переворачивается и в обратную сторону.
3-ий способ транспонирования — сводная таблица
Третий способ транспонирования данных в Excel — с помощью сводной таблицы. Этот способ транспонирования работает только в одном направлении — из столбцов переворачивает данные в строки. Но его преимущество, по сравнению с предыдущими, — это возможность фильтровать данные и использовать всю мощь сводных таблиц.
Сначала необходимо сделать сводную таблицу. Выделяем исходные данные:
Заходим в меню «Вставка» и выбираем пункт «Сводная таблица», и в диалоговом окне сводной нажимаем «ОК»:
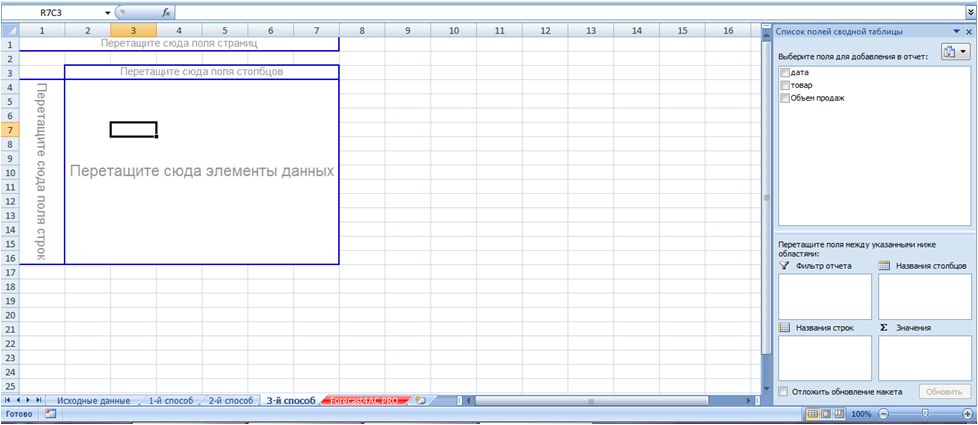
В новом листе создается сводная таблица:
В названия столбцов перетаскиваем поля «дата» и «товар», в значения перетаскиваем «объем продаж».
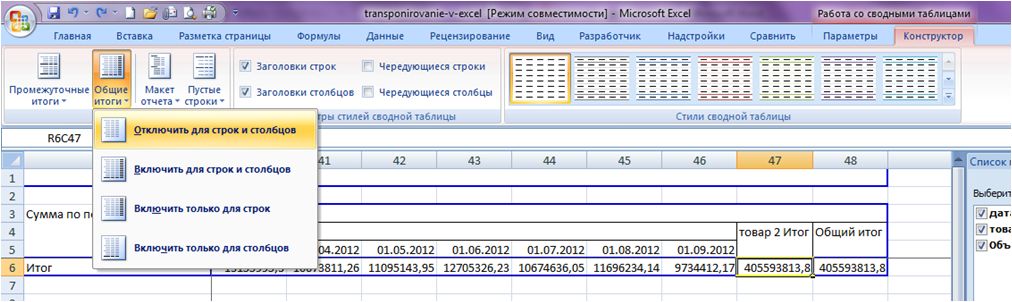
В меню «Конструктор» отключаем общие и промежуточные итоги. Меню «Конструктор» появляется в Excel при постановке курсора на сводную таблицу.
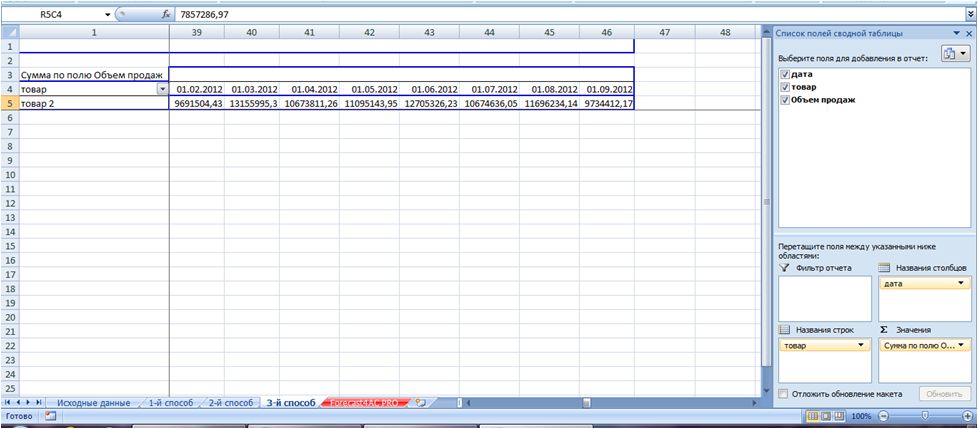
И получаем перевернутые данные:
Для удобства поле «Товары» мы можем перенести в область строк, и получить более рабочий вид кросс таблицы:
Мы рассмотрели 3 способа транспонирования данных.
Для того, чтобы сделать расчет с помощью программы Forecast4AC PRO, данные временного ряда необходимо представить в виде строки. Вы можете воспользоваться любым предложенным способом — программа будет работать и со сводной, и с формулами или ссылками и с обычными значениями, представленными в виде кросс таблицы!
Воспользовавшись Forecast4AC PRO в листе «3-й способ», мы построили график, на который выведена «Модель прогноза», «Исходные данные», «Границы прогноза», и «Тренд».
Точных Вам прогнозов и хорошего настроения!
Скачать пример транспонирования в Excel
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.