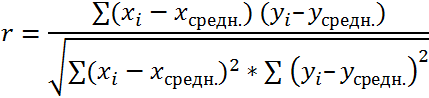Коэффициент корреляции отражает степень взаимосвязи между двумя показателями. Всегда принимает значение от -1 до 1. Если коэффициент расположился около 0, то говорят об отсутствии связи между переменными.
Если значение близко к единице (от 0,9, например), то между наблюдаемыми объектами существует сильная прямая взаимосвязь. Если коэффициент близок к другой крайней точке диапазона (-1), то между переменными имеется сильная обратная взаимосвязь. Когда значение находится где-то посередине от 0 до 1 или от 0 до -1, то речь идет о слабой связи (прямой или обратной). Такую взаимосвязь обычно не учитывают: считается, что ее нет.
Расчет коэффициента корреляции в Excel
Рассмотрим на примере способы расчета коэффициента корреляции, особенности прямой и обратной взаимосвязи между переменными.
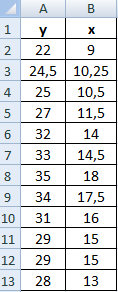
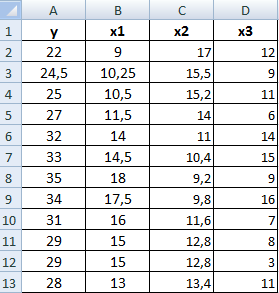
Значения показателей x и y:
Y – независимая переменная, x – зависимая. Необходимо найти силу (сильная / слабая) и направление (прямая / обратная) связи между ними. Формула коэффициента корреляции выглядит так:
Чтобы упростить ее понимание, разобьем на несколько несложных элементов.
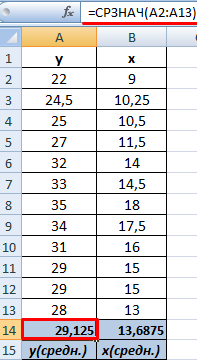
- Найдем средние значения переменных, используя функцию СРЗНАЧ:
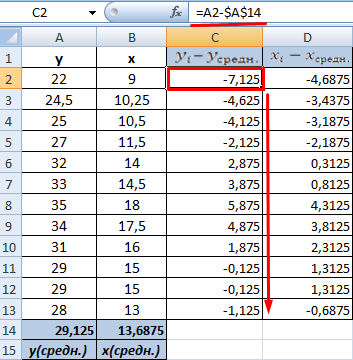
- Посчитаем разницу каждого y и yсредн., каждого х и хсредн. Используем математический оператор «-».
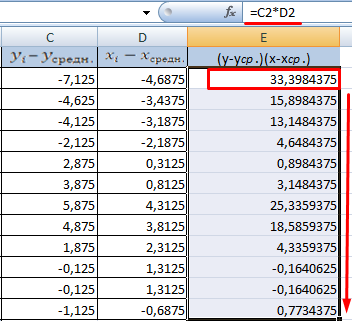
- Теперь перемножим найденные разности:
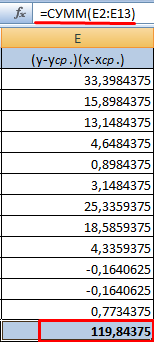
- Найдем сумму значений в данной колонке. Это и будет числитель.
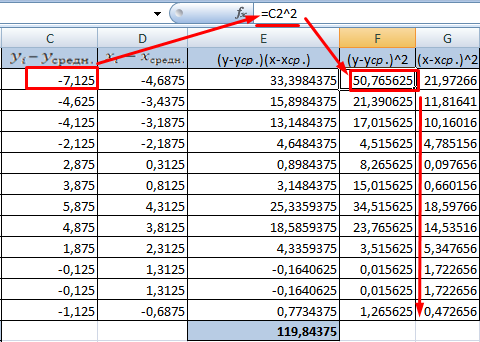
- Для расчета знаменателя разницы y и y-средн., х и х-средн. Нужно возвести в квадрат.
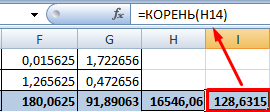
- Находим суммы значений в полученных колонках (с помощью функции АВТОСУММА). Перемножаем их. Результат возводим в квадрат (функция КОРЕНЬ).
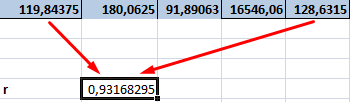
- Осталось посчитать частное (числитель и знаменатель уже известны).
Между переменными определяется сильная прямая связь.
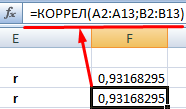
Встроенная функция КОРРЕЛ позволяет избежать сложных расчетов. Рассчитаем коэффициент парной корреляции в Excel с ее помощью. Вызываем мастер функций. Находим нужную. Аргументы функции – массив значений y и массив значений х:
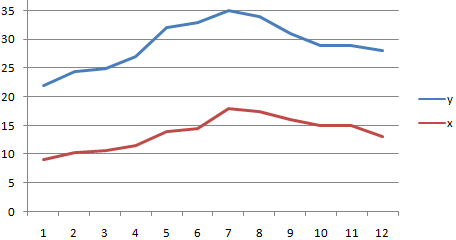
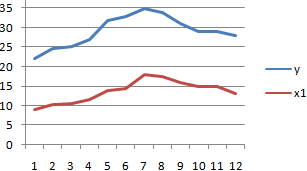
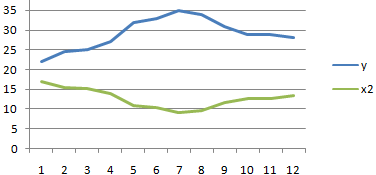
Покажем значения переменных на графике:
Видна сильная связь между y и х, т.к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
Матрица парных коэффициентов корреляции в Excel
Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.
Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
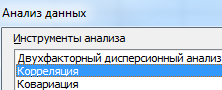
- На вкладке «Данные» в группе «Анализ» открываем пакет «Анализ данных» (для версии 2007). Если кнопка недоступна, нужно ее добавить («Параметры Excel» — «Надстройки»). В списке инструментов анализа выбираем «Корреляция».
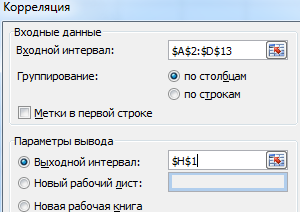
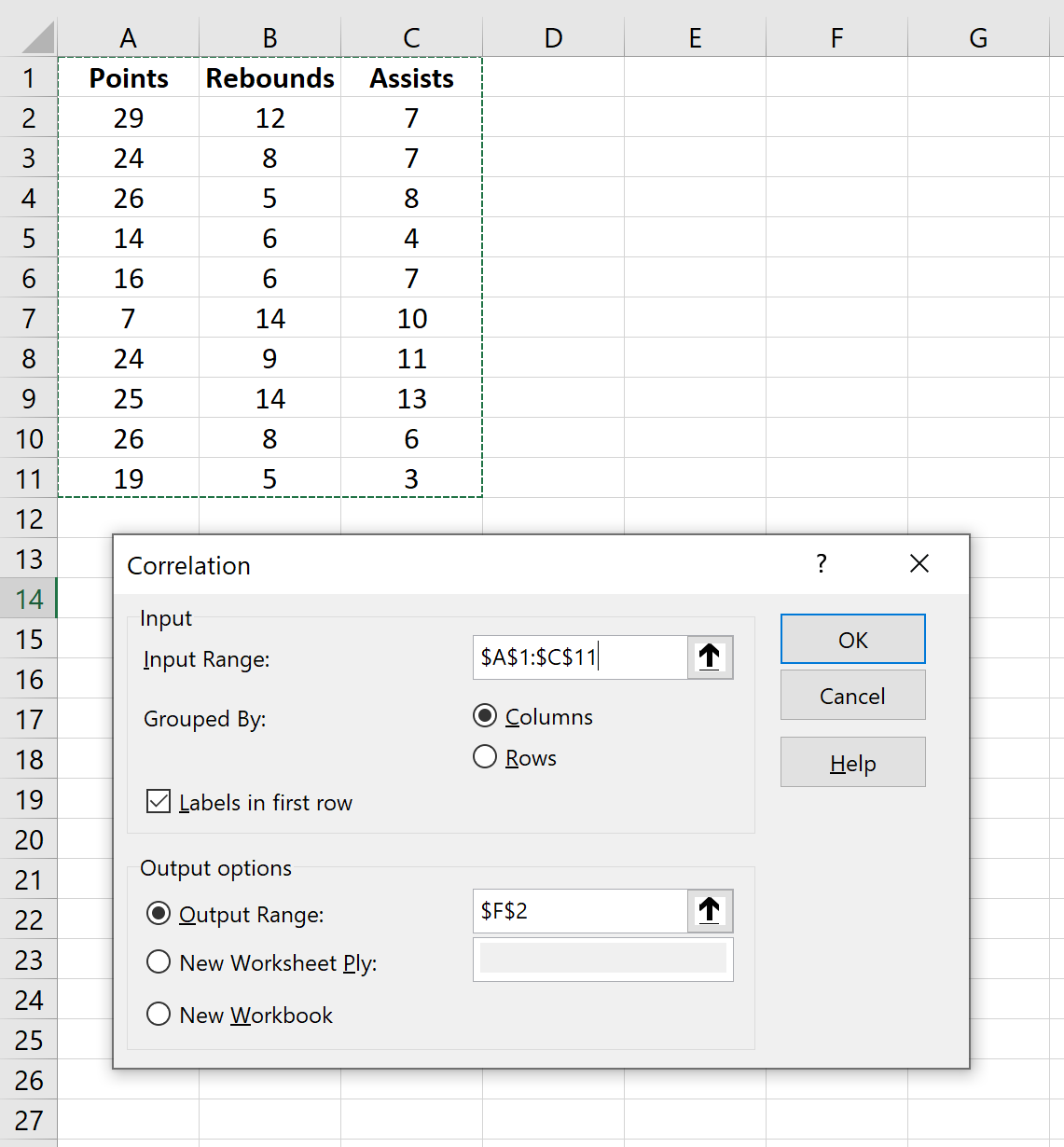
- Нажимаем ОК. Задаем параметры для анализа данных. Входной интервал – диапазон ячеек со значениями. Группирование – по столбцам (анализируемые данные сгруппированы в столбцы). Выходной интервал – ссылка на ячейку, с которой начнется построение матрицы. Размер диапазона определится автоматически.
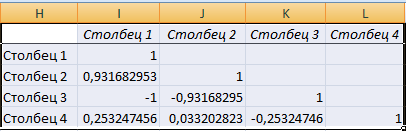
- После нажатия ОК в выходном диапазоне появляется корреляционная матрица. На пересечении строк и столбцов – коэффициенты корреляции. Если координаты совпадают, то выводится значение 1.
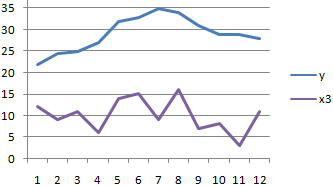
Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.
Изобразим наглядно корреляционные отношения с помощью графиков.
- Сильная прямая связь между y и х1.
- Сильная обратная связь между y и х2. Изменения значений происходят параллельно друг другу. Но если y растет, х падает. Значения y увеличиваются – значения х уменьшаются.
- Отсутствие взаимосвязи между значениями y и х3. Изменения х3 происходят хаотично и никак не соотносятся с изменениями y.
Скачать вычисление коэффициента парной корреляции в Excel
Для чего нужен такой коэффициент? Для определения взаимосвязи между наблюдаемыми явлениями и составления прогнозов.
17 авг. 2022 г.
читать 3 мин
Одним из способов количественной оценки связи между двумя переменными является использованиекоэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными .
Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных.
В этих случаях мы можем создать матрицу корреляции , представляющую собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими попарными комбинациями переменных.
В этом руководстве объясняется, как создать и интерпретировать корреляционную матрицу в Excel.
Как создать корреляционную матрицу в Excel
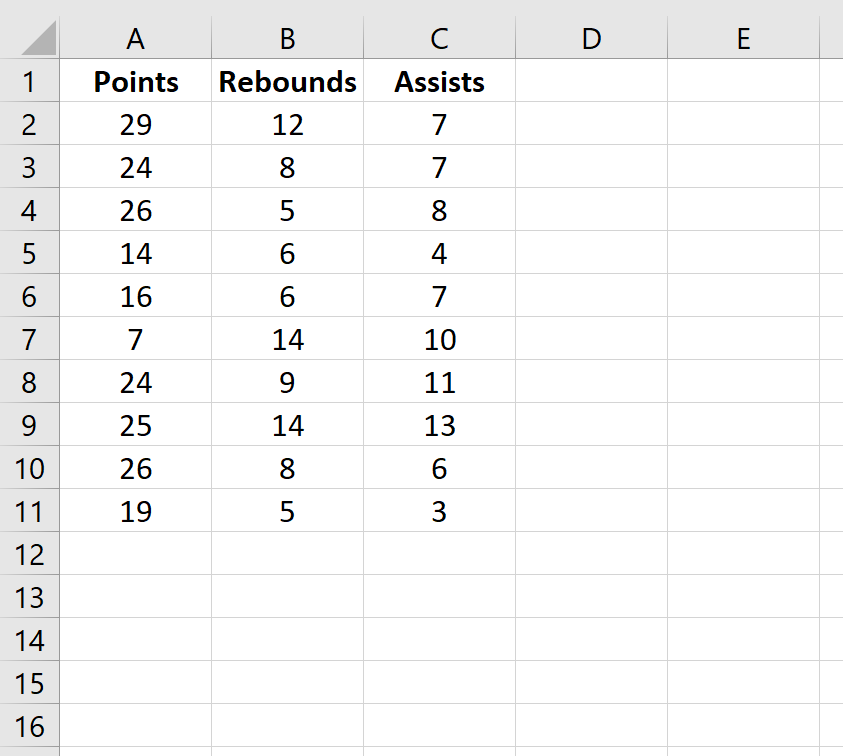
Предположим, у нас есть следующий набор данных, который показывает среднее количество очков, подборов и передач для 10 баскетболистов:
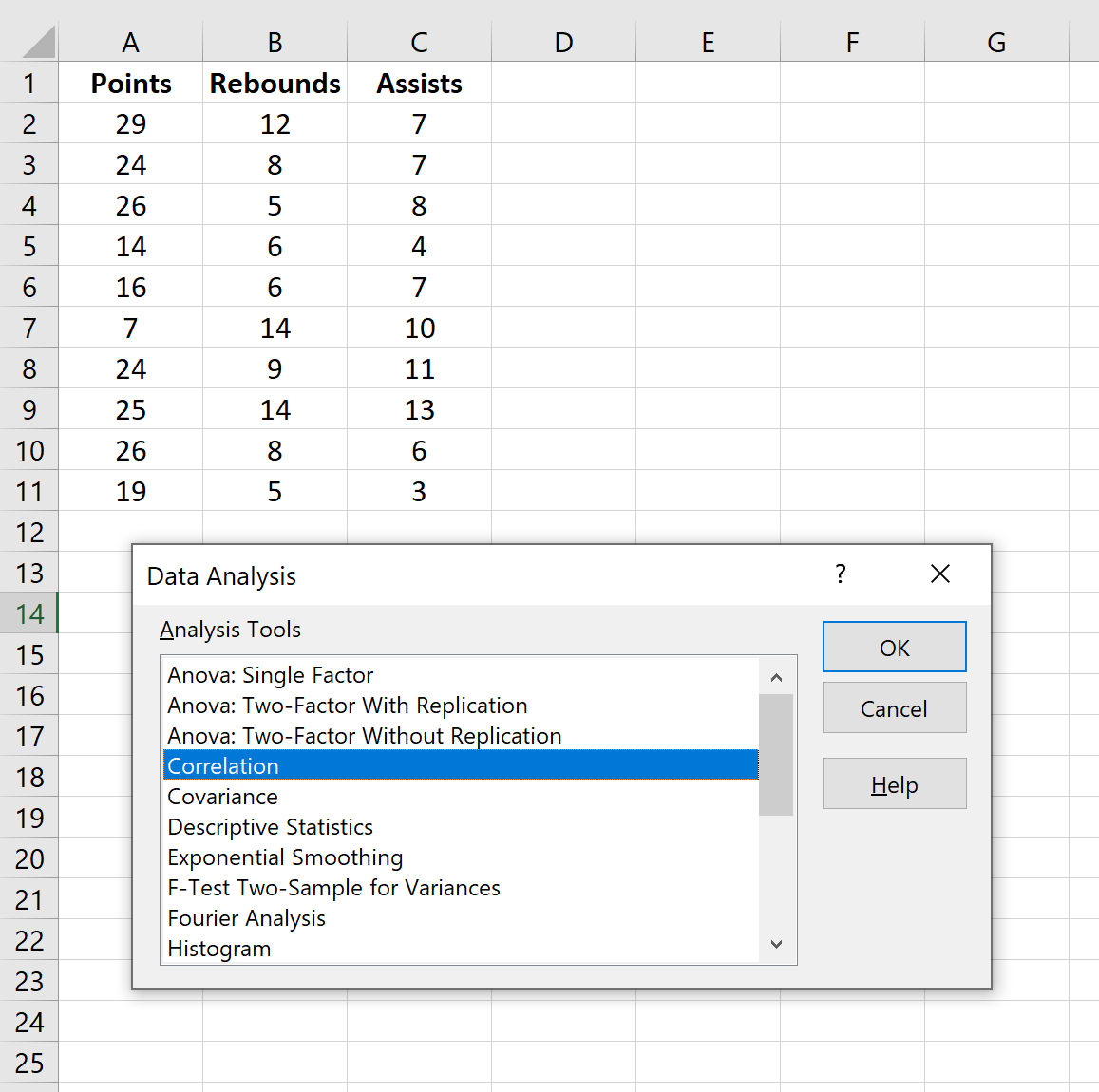
Чтобы создать матрицу корреляции для этого набора данных, перейдите на вкладку « Данные » на верхней ленте Excel и нажмите « Анализ данных» .
Если вы не видите эту опцию, вам нужно сначала загрузить бесплатный пакет инструментов анализа данных в Excel .
В новом появившемся окне выберите « Корреляция » и нажмите « ОК ».
Для Input Range выберите ячейки, в которых находятся данные (включая первую строку с метками). Установите флажок рядом с Метки в первой строке.Для выходного диапазона выберите ячейку, в которой вы хотите разместить корреляционную матрицу. Затем нажмите ОК .
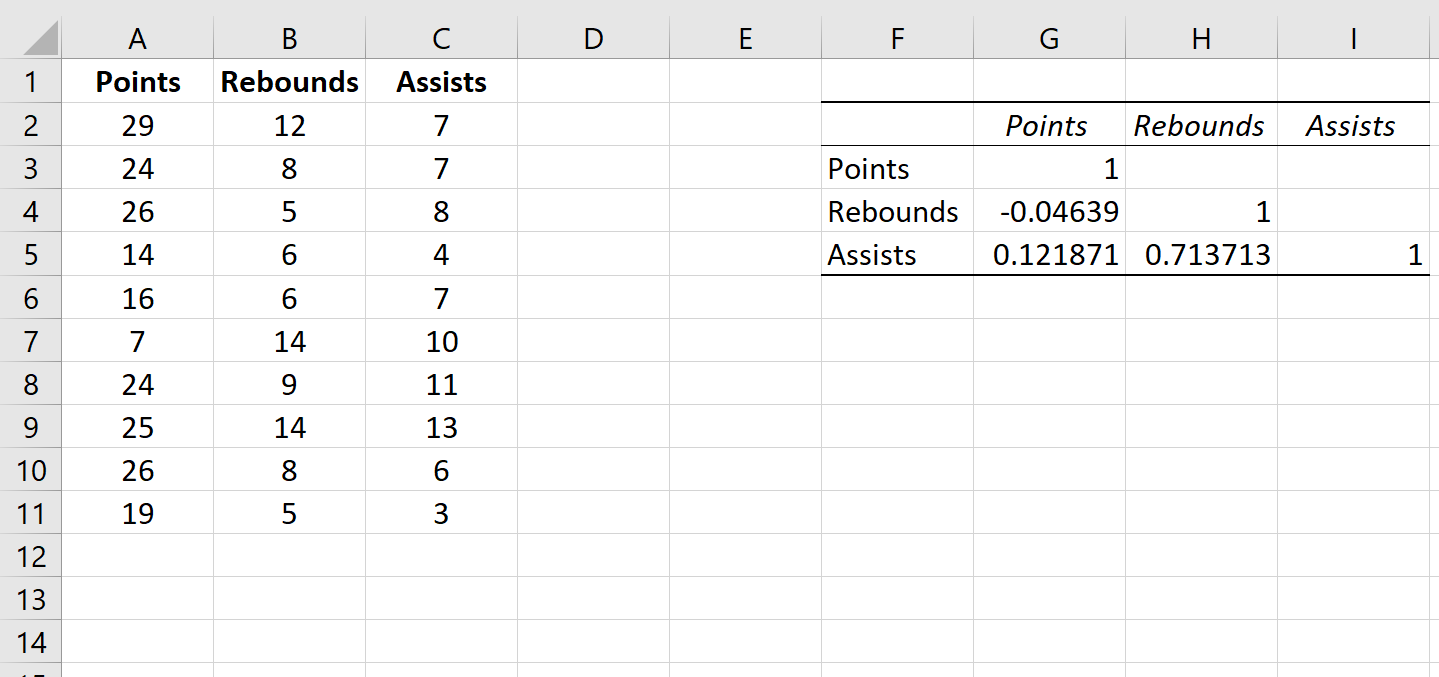
Это автоматически создаст следующую корреляционную матрицу:
Как интерпретировать матрицу корреляции в Excel
Значения в отдельных ячейках корреляционной матрицы сообщают нам коэффициент корреляции Пирсона между каждой парной комбинацией переменных. Например:
Корреляция между очками и подборами: -0,04639. Очки и подборы имеют небольшую отрицательную корреляцию, но это значение настолько близко к нулю, что нет убедительных доказательств значимой связи между этими двумя переменными.
Соотношение очков и передач: 0,121871. Очки и передачи имеют небольшую положительную корреляцию, но это значение также довольно близко к нулю, поэтому нет убедительных доказательств значимой связи между этими двумя переменными.
Корреляция между подборами и передачами: 0,713713. Подборы и передачи имеют сильную положительную корреляцию. То есть игроки, у которых больше подборов, как правило, и чаще делают передачи.
Обратите внимание, что диагональные значения в матрице корреляции равны 1, потому что корреляция между переменной и самой собой всегда равна 1. На практике интерпретировать это число бесполезно.
Бонус: визуализация коэффициентов корреляции
Один из простых способов визуализировать значение коэффициентов корреляции в таблице — применить условное форматирование к таблице.
На верхней ленте в Excel перейдите на вкладку « Главная », затем в группу « Стили ».
Нажмите « Таблица условного форматирования » , затем нажмите « Цветовые шкалы » , затем нажмите « Цветовая шкала зелено-желто-красный» .
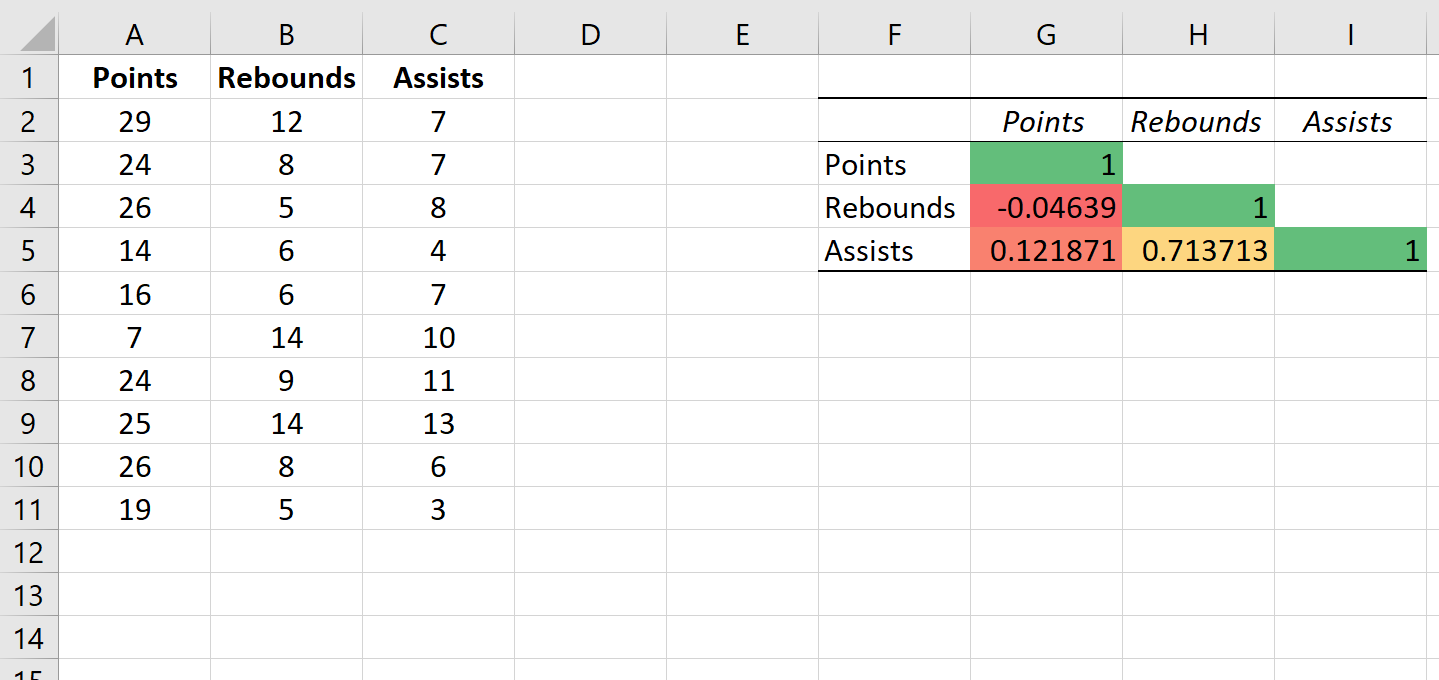
Это автоматически применяет следующую цветовую шкалу к корреляционной матрице:
Это помогает нам легко визуализировать силу корреляции между переменными.
Это особенно полезный прием, если мы работаем с корреляционной матрицей с большим количеством переменных, потому что она помогает нам быстро определить переменные, которые имеют самые сильные корреляции.
По теме: Что считается «сильной» корреляцией?
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как создать матрицу диаграммы рассеяния в Excel
Как выполнить корреляционный тест в Excel
Содержание
- Вычисление множественного коэффициента корреляции
- Этап 1: активация пакета анализа
- Этап 2: расчет коэффициента
- Этап 3: анализ полученного результата
- Вопросы и ответы
Для определения степени зависимости между несколькими показателями применяется множественные коэффициенты корреляции. Их затем сводят в отдельную таблицу, которая имеет название корреляционной матрицы. Наименованиями строк и столбцов такой матрицы являются названия параметров, зависимость которых друг от друга устанавливается. На пересечении строк и столбцов располагаются соответствующие коэффициенты корреляции. Давайте выясним, как можно провести подобный расчет с помощью инструментов Excel.
Читайте также: Корреляционный анализ в Экселе
Вычисление множественного коэффициента корреляции
Принято следующим образом определять уровень взаимосвязи между различными показателями, в зависимости от коэффициента корреляции:
- 0 – 0,3 – связь отсутствует;
- 0,3 – 0,5 – связь слабая;
- 0,5 – 0,7 – средняя связь;
- 0,7 – 0,9 – высокая;
- 0,9 – 1 – очень сильная.
Если корреляционный коэффициент отрицательный, то это значит, что связь параметров обратная.
Для того, чтобы составить корреляционную матрицу в Экселе, используется один инструмент, входящий в пакет «Анализ данных». Он так и называется – «Корреляция». Давайте узнаем, как с помощью него можно вычислить показатели множественной корреляции.
Этап 1: активация пакета анализа
Сразу нужно сказать, что по умолчанию пакет «Анализ данных» отключен. Поэтому, прежде чем приступить к процедуре непосредственного вычисления коэффициентов корреляции, нужно его активировать. К сожалению, далеко не каждый пользователь знает, как это делать. Поэтому мы остановимся на данном вопросе.
- Переходим во вкладку «Файл». В левом вертикальном меню окна, которое откроется после этого, щелкаем по пункту «Параметры».
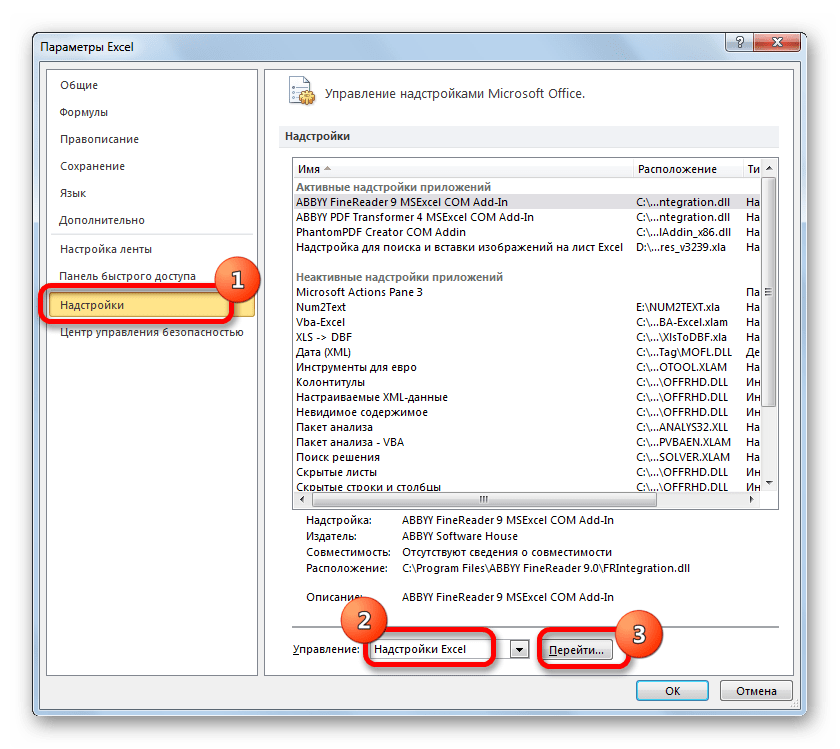
- После запуска окна параметров посредством его левого вертикального меню переходим в раздел «Надстройки». Там в самом низу правой части окна располагается поле «Управление». Переставляем переключатель в нём в позицию «Надстройки Excel», если отображен другой параметр. После этого клацаем по кнопке «Перейти…», находящейся справа от указанного поля.
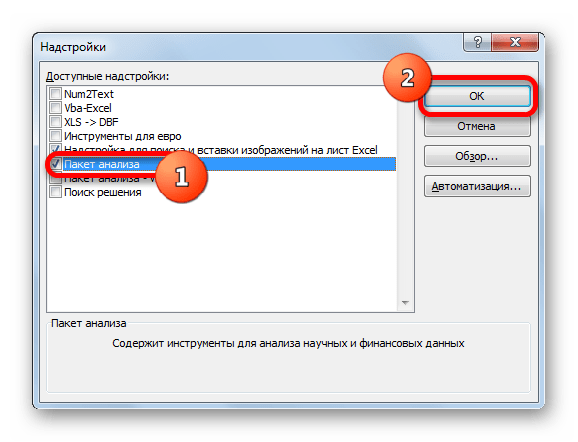
- Происходит запуск небольшого окошка «Надстройки». Устанавливаем флажок около параметра «Пакет анализа». Затем в правой части окна кликаем по кнопке «OK».
После указанного действия пакет инструментов «Анализ данных» будет активирован.
Этап 2: расчет коэффициента
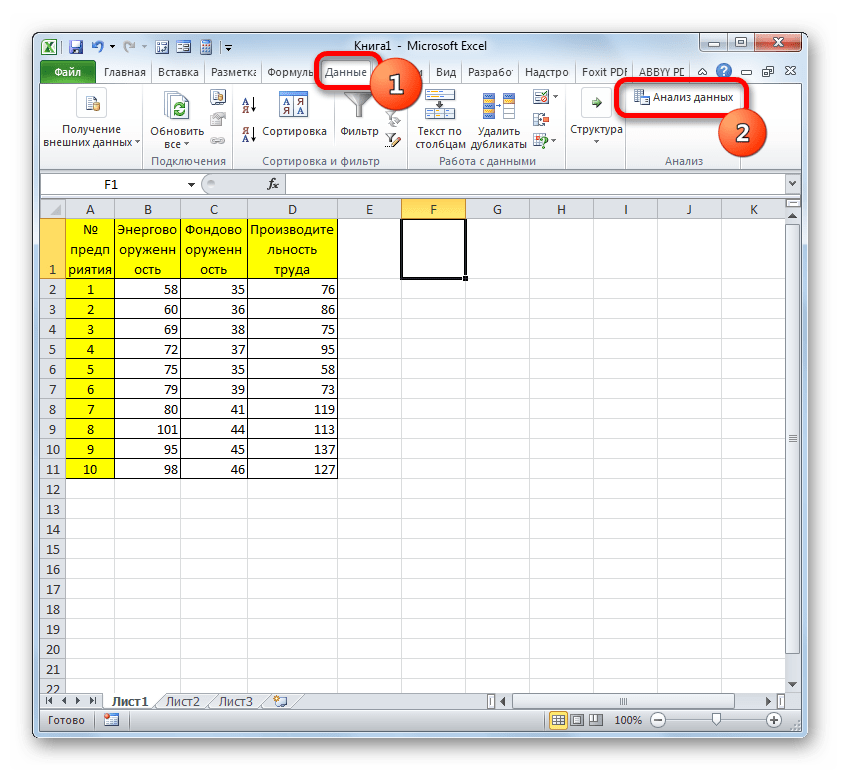
Теперь можно переходить непосредственно к расчету множественного коэффициента корреляции. Давайте на примере представленной ниже таблицы показателей производительности труда, фондовооруженности и энерговооруженности на различных предприятиях рассчитаем множественный коэффициент корреляции указанных факторов.
- Перемещаемся во вкладку «Данные». Как видим, на ленте появился новый блок инструментов «Анализ». Клацаем по кнопке «Анализ данных», которая располагается в нём.
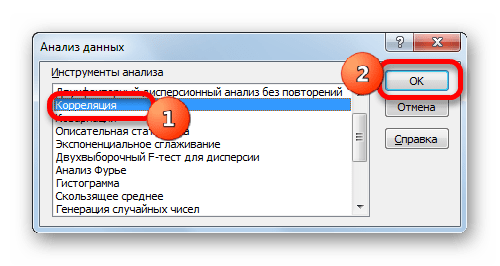
- Открывается окошко, которое носит наименование «Анализ данных». Выделяем в списке инструментов, расположенных в нём, наименование «Корреляция». После этого щелкаем по кнопке «OK» в правой части интерфейса окна.
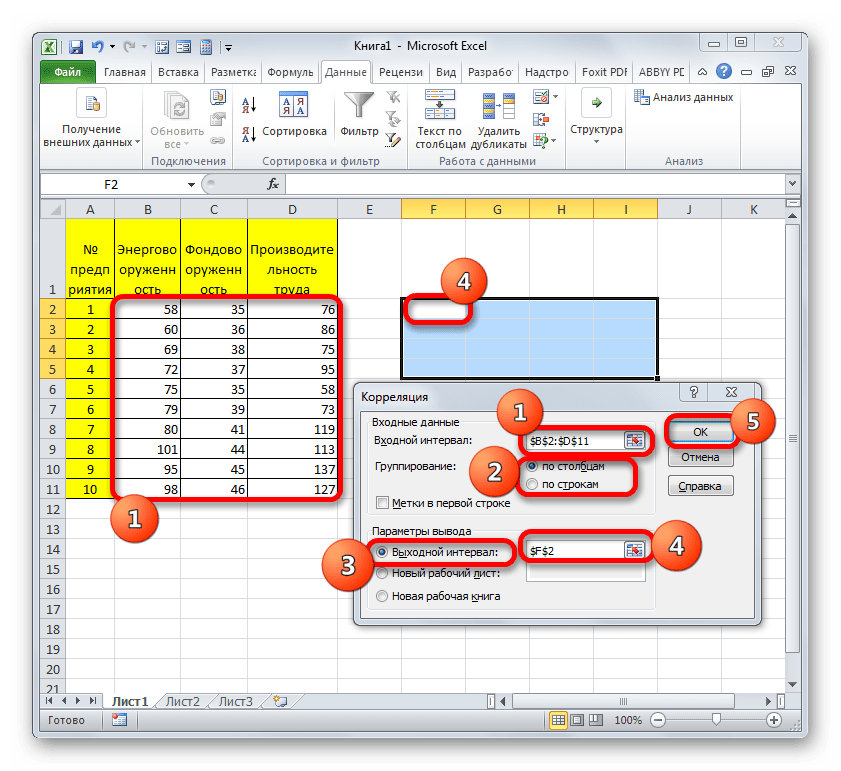
- Открывается окно инструмента «Корреляция». В поле «Входной интервал» следует внести адрес диапазона таблицы, в котором расположены данные по трем изучаемым факторам: энерговооруженность, фондовооруженность и производительность. Можно произвести ручное внесение координат, но легче просто установить курсор в поле и, зажав левую кнопку мыши, выделить соответствующую область таблицы. После этого адрес диапазона будет отображен в поле окна «Корреляция».
Так как у нас факторы разбиты по столбцам, а не по строкам, то в параметре «Группирование» выставляем переключатель в позицию «По столбцам». Впрочем, он там уже и так установлен по умолчанию. Поэтому остается только проверить правильность его расположения.
Около пункта «Метки в первой строке» галочку ставить не обязательно. Поэтому мы пропустим данный параметр, так как он не повлияет на общий характер расчета.
В блоке настроек «Параметр вывода» следует указать, где именно будет располагаться наша корреляционная матрица, в которую выводится результат расчета. Доступны три варианта:
- Новая книга (другой файл);
- Новый лист (при желании в специальном поле можно дать ему наименование);
- Диапазон на текущем листе.
Давайте выберем последний вариант. Переставляем переключатель в положение «Выходной интервал». В этом случае в соответствующем поле нужно указать адрес диапазона матрицы или хотя бы её верхнюю левую ячейку. Устанавливаем курсор в поле и клацаем по ячейке на листе, которую планируем сделать верхним левым элементом диапазона вывода данных.
После выполнения всех указанных манипуляций остается только щелкнуть по кнопке «OK» в правой части окошка «Корреляция».
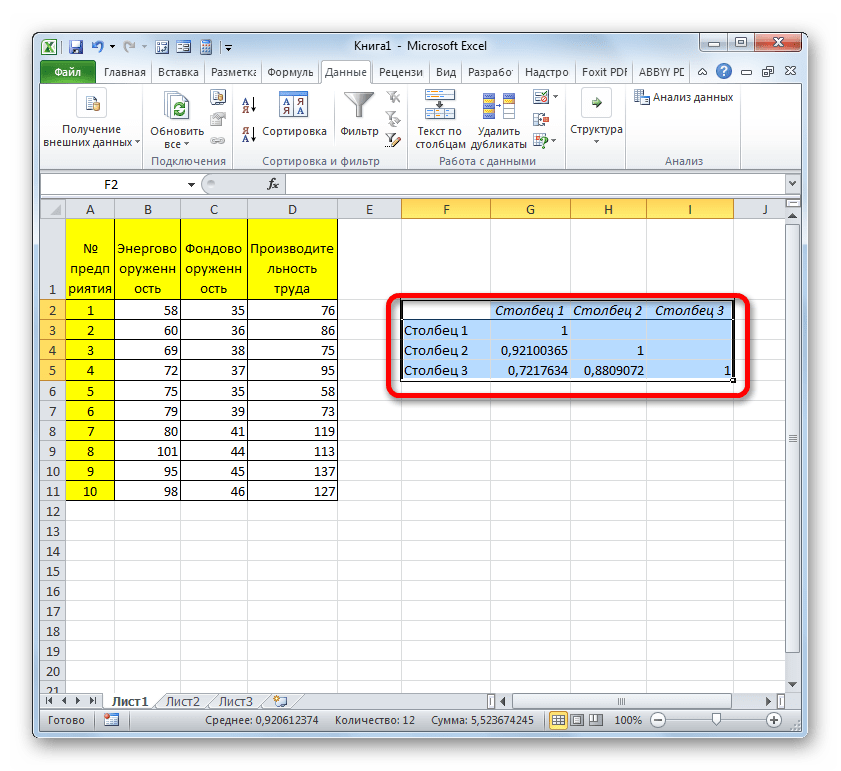
- После выполнения последнего действия Excel строит матрицу корреляции, заполняя её данными, в указанном пользователем диапазоне.
Этап 3: анализ полученного результата
Теперь давайте разберемся, как понимать тот результат, который мы получили в процессе обработки данных инструментом «Корреляция» в программе Excel.
Как видим из таблицы, коэффициент корреляции фондовооруженности (Столбец 2) и энерговооруженности (Столбец 1) составляет 0,92, что соответствует очень сильной взаимосвязи. Между производительностью труда (Столбец 3) и энерговооруженностью (Столбец 1) данный показатель равен 0,72, что является высокой степенью зависимости. Коэффициент корреляции между производительностью труда (Столбец 3) и фондовооруженностью (Столбец 2) равен 0,88, что тоже соответствует высокой степени зависимости. Таким образом, можно сказать, что зависимость между всеми изучаемыми факторами прослеживается довольно сильная.
Как видим, пакет «Анализ данных» в Экселе представляет собой очень удобный и довольно легкий в обращении инструмент для определения множественного коэффициента корреляции. С его же помощью можно производить расчет и обычной корреляции между двумя факторами.
Еще статьи по данной теме:
Помогла ли Вам статья?
One way to quantify the relationship between two variables is to use the Pearson correlation coefficient, which is a measure of the linear association between two variables.
It has a value between -1 and 1 where:
- -1 indicates a perfectly negative linear correlation between two variables
- 0 indicates no linear correlation between two variables
- 1 indicates a perfectly positive linear correlation between two variables
The further away the correlation coefficient is from zero, the stronger the relationship between the two variables.
But in some cases we want to understand the correlation between more than just one pair of variables.
In these cases, we can create a correlation matrix, which is a square table that shows the the correlation coefficients between several pairwise combination of variables.
This tutorial explains how to create and interpret a correlation matrix in Excel.
How to Create a Correlation Matrix in Excel
Suppose we have the following dataset that shows the average numbers of points, rebounds, and assists for 10 basketball players:
To create a correlation matrix for this dataset, go to the Data tab along the top ribbon of Excel and click Data Analysis.
If you don’t see this option, then you need to first load the free Data Analysis Toolpak in Excel.
In the new window that pops up, select Correlation and click OK.
For Input Range, select the cells where the data is located (including the first row with the labels). Check the box next to Labels in first row. For Output Range, select a cell where you’d like the correlation matrix to appear. Then click OK.
This will automatically produce the following correlation matrix:
How to Interpret a Correlation Matrix in Excel
The values in the individual cells of the correlation matrix tell us the Pearson Correlation Coefficient between each pairwise combination of variables. For example:
Correlation between Points and Rebounds: -0.04639. Points and rebounds are slightly negatively correlated, but this value is so close to zero that there isn’t strong evidence for a significant association between these two variables.
Correlation between Points and Assists: 0.121871. Points and assists are slightly positively correlated, but this value also is fairly close to zero so there isn’t strong evidence for a significant association between these two variables.
Correlation between Rebounds and Assists: 0.713713. Rebounds and assists are strongly positively correlated. That is, players who have more rebounds also tend to have more assists.
Notice that the diagonal values in the correlation matrix are all equal to 1 because the correlation between a variable and itself is always 1. In practice, this number isn’t useful to interpret.
Bonus: Visualizing Correlation Coefficients
One easy way to visualize the value of the correlation coefficients in the table is to apply Conditional Formatting to the table.
Along the top ribbon in Excel, go to the Home tab, then the Styles group.
Click Conditional Formatting Chart, then click Color Scales, then click the Green-Yellow-Red Color Scale.
This automatically applies the following color scale to the correlation matrix:
This helps us easily visualize the strength of the correlations between the variables.
This is a particularly helpful trick if we’re working with a correlation matrix that has a lot of variables because it helps us quickly identify the variables that have the strongest correlations.
Related: What is Considered to Be a “Strong” Correlation?
Additional Resources
The following tutorials explain how to perform other common tasks in R:
How to Create a Scatterplot Matrix in Excel
How to Perform a Correlation Test in Excel
На чтение 3 мин. Просмотров 151 Опубликовано 21.01.2021
Опубликовано 5 июля 2020 г. Заком
Один из способов количественно определить взаимосвязь между двумя переменными – использовать коэффициент корреляции Пирсона, который является мерой линейной связи между двумя переменными . Он имеет значение от -1 до 1, где:
- -1 указывает на абсолютно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на абсолютно положительную линейную корреляцию между двумя переменными
Чем дальше коэффициент корреляции от нуля, тем более сильная связь между двумя переменными.
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных. В этих случаях мы можем создать матрицу корреляции, которая представляет собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими попарными комбинациями переменных.
В этом руководстве объясняется, как создать и интерпретировать матрицу корреляции в Excel.
Содержание
- Как создать матрицу корреляции в Excel
- Как интерпретировать матрицу корреляции в Excel
- Бонус: визуализация коэффициентов корреляции
Как создать матрицу корреляции в Excel
Предположим, у нас есть следующий набор данных, который показывает среднее количество очков, подборов и передач для 10 баскетболистов:

Чтобы создать матрицу корреляции для этого набора данных, перейдите на вкладку Данные на верхней ленте Excel и нажмите Анализ данных .

Если вы не видите этот параметр, вам необходимо сначала загрузить бесплатный пакет инструментов анализа данных в Excel .
В новом всплывающем окне выберите Корреляция и нажмите OK .

Для Диапазон ввода выберите ячейки, в которых расположены данные (включая первую строку с метками). Установите флажок рядом с Ярлыки в первой строке . Для Диапазон вывода выберите ячейку, в которой должна отображаться матрица корреляции. Затем нажмите OK .

Это автоматически создаст следующую матрицу корреляции:

Как интерпретировать матрицу корреляции в Excel
Значения в отдельных ячейках матрицы корреляции сообщают нам коэффициент корреляции Пирсона между каждой попарной комбинацией переменных. Например:
Корреляция между очками и отскоками: -0,04639. Очки и подборы имеют небольшую отрицательную корреляцию, но это значение настолько близко к нулю, что нет убедительных доказательств значимой связи между этими двумя переменными..
Соотношение очков и передач: 0,121871. Очки и передачи имеют слегка положительную корреляцию, но это значение также довольно близко к нулю, поэтому нет убедительных доказательств значимой связи между этими двумя переменными.
Корреляция между отскоками и ассисты: 0,713713. Подборы и передачи сильно взаимосвязаны. То есть игроки, у которых больше подборов, также, как правило, получают больше передач.
Обратите внимание, что все диагональные значения в корреляционной матрице равны 1, потому что корреляция между переменной и самой собой всегда равна 1. На практике это число бесполезно интерпретировать.
Бонус: визуализация коэффициентов корреляции
Один простой способ визуализировать Значение коэффициентов корреляции в таблице заключается в применении к таблице Условное форматирование . В верхней части ленты Excel перейдите на вкладку Главная , затем в группу Стили . Нажмите Диаграмма условного форматирования , затем нажмите Цветовые шкалы , затем нажмите Зеленая-желто-красная цветовая шкала .
Это автоматически применяет следующую цветовую шкалу к матрице корреляции:

Это помогает нам легко визуализировать силу корреляции между переменными. Это особенно полезный трюк, если мы работаем с корреляционной матрицей, содержащей множество переменных, потому что она помогает нам быстро идентифицировать переменные с наиболее сильными корреляциями.