Функция ЧАСТОТА используется для определения количества вхождения определенных величин в заданный интервал и возвращает данные в виде массива значений. Используя функцию ЧАСТОТА, мы узнаем, как посчитать частоту в Excel.
Пример использования функции ЧАСТОТА в Excel
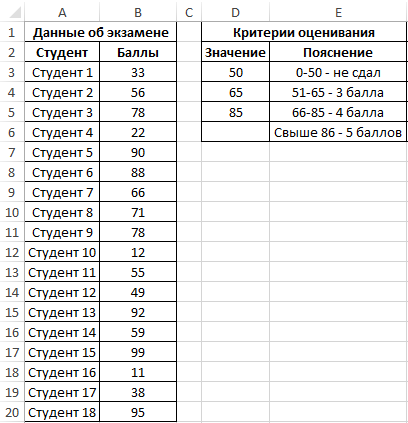
Пример 1. Студенты одной из групп в университете сдали экзамен по физике. При оценке качества сдачи экзамена используется 100-бальная система. Для определения окончательной оценки по 5-бальной системе используют следующие критерии:
- От 0 до 50 баллов – экзамен не сдан.
- От 51 до 65 баллов – оценка 3.
- От 66 до 85 баллов – оценка 4.
- Свыше 86 баллов – оценка 5.
Для статистики необходимо определить, сколько студентов получили 5, 4, 3 баллов и количество тех, кому не удалось сдать экзамен.
Внесем данные в таблицу:
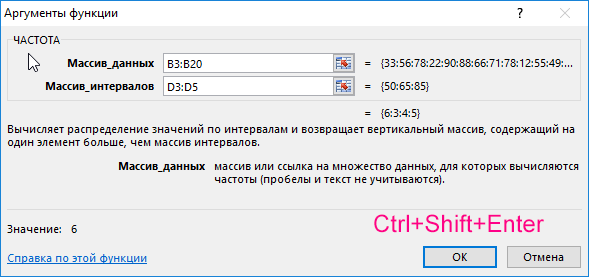
Для решения выделим области из 4 ячеек и введем следующую функцию:
Описание аргументов:
- B3:B20 – массив данных об оценках студентов;
- D3:D5 – массив критериев нахождения частоты вхождений в массиве данных об оценках.
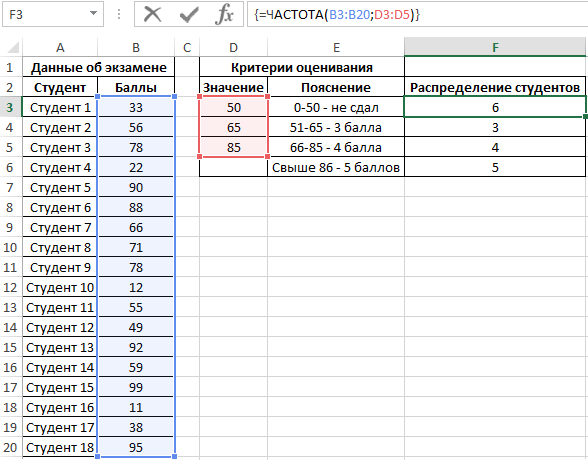
Выделяем диапазон F3:F6 жмем сначала клавишу F2, а потом комбинацию клавиш Ctrl+Shift+Enter, чтобы функция ЧАСТОТА была выполнена в массиве. Подтверждением того что все сделано правильно будут служить фигурные скобки {} в строке формул по краям. Это значит, что формула выполняется в массиве. В результате получим:
То есть, 6 студентов не сдали экзамен, оценки 3, 4 и 5 получили 3, 4 и 5 студентов соответственно.
Пример определения вероятности используя функцию ЧАСТОТА в Excel
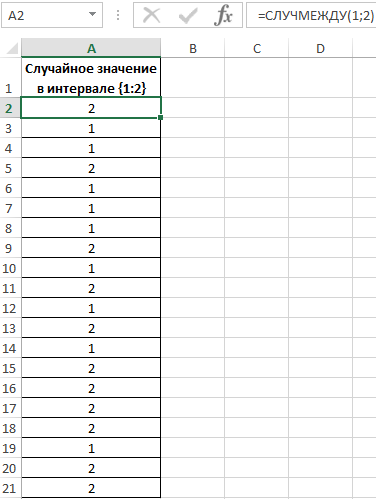
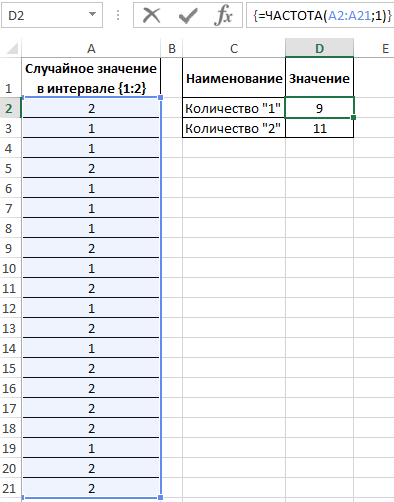
Пример 2. Известно то, что если существует только два возможных варианта развития событий, вероятности первого и второго равны 0,5 соответственно. Например, вероятности выпадения «орла» или «решки» у подброшенной монетки равны ½ и ½ (если пренебречь возможностью падения монетки на ребро). Аналогичное расчетное распределение вероятностей характерно для следующей функции СЛУЧМЕЖДУ(1;2), которая возвращает случайное число в интервале от 1 до 2. Было проведено 20 вычислений с использованием данной функции. Определить фактические вероятности появления чисел 1 и 2 соответственно на основании полученных результатов.
Заполним исходную таблицу случайными значениями от 1-го до 2-ух:
Для определения случайных значений в исходной таблице была использована специальная функция:
=СЛУЧМЕЖДУ(1;2)
Для определения количества сгенерированных 1 и 2 используем функцию:
=ЧАСТОТА(A2:A21;1)
Описание аргументов:
- A2:A21 – массив сгенерированных функцией =СЛУЧМЕЖДУ(1;2) значений;
- 1 – критерий поиска (функция ЧАСТОТА ищет значения от 0 до 1 включительно и значения >1).
В результате получим:
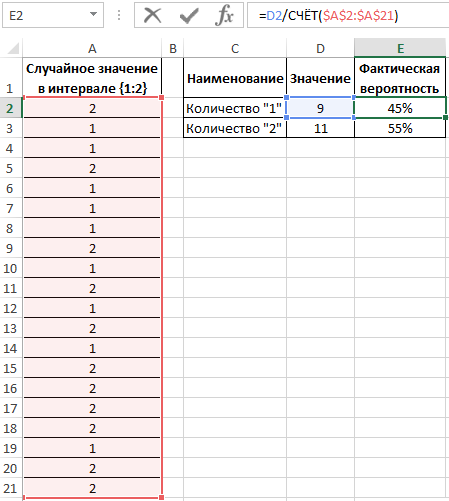
Вычислим вероятности, разделив количество событий каждого типа на общее их число:
Для подсчета количества событий используем функцию =СЧЁТ($A$2:$A$21). Или можно просто разделить на значение 20. Если заранее не известно количество событий и размер диапазона со случайными значениями, тогда можно использовать в аргументах функции СЧЁТ ссылку на целый столбец: =СЧЁТ(A:A). Таким образом будет автоматически подсчитывается количество чисел в столбце A.
Вероятности выпадения «1» и «2» — 0,45 и 0,55 соответственно. Не забудьте присвоить ячейкам E2:E3 процентный формат для отображения их значений в процентах: 45% и 55%.
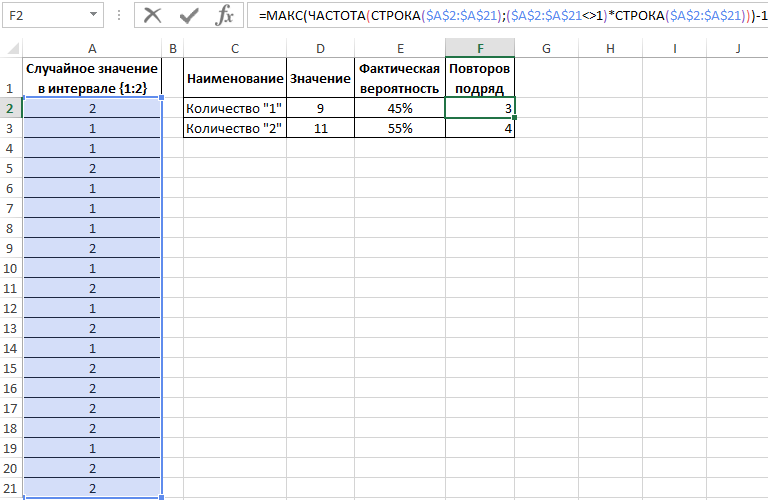
Теперь воспользуемся более сложной формулой для вычисления максимальной частоты повторов:
Формулы в ячейках F2 и F3 отличаются только одним лишь числом после оператора сравнения «не равно»: <>1 и <>2.
Интересный факт! С помощью данной формулы можно легко проверить почему не работает стратегия удвоения ставок в рулетке казино. Данную стратегию управления ставками в азартных играх называют еще Мартингейл. Дело в том, что количество случайных повторов подряд может достигать 18-ти раз и более, то есть восемнадцать раз подряд красные или черные. Например, если ставку в 2 доллара 18 раз удваивать – это уже более пол миллиона долларов «просадки». Это уже провал по любым техникам планирования рисков. Так же следует учитывать, что кроме «черные» и «красные» иногда выпадает еще и «зеро», что окончательно уничтожает все шансы. Так же интересно, что сумма всех чисел в рулетке от 0 до 36 равна 666.
Как посчитать неповторяющиеся значения в Excel?
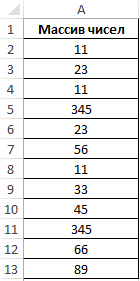
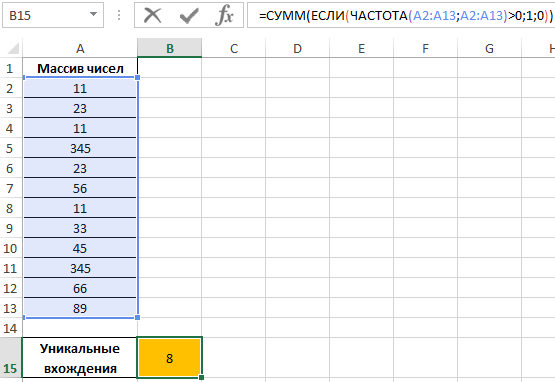
Пример 3. Определить количество уникальных вхождений в массив числовых данных, то есть не повторяющихся значений.
Исходная таблица:
Определим искомую величину с помощью формулы:
В данном случае функция ЧАСТОТА выполняет проверку наличия каждого из элементов массива данных в этом же массиве данных (оба аргумента совпадают). С помощью функции ЕСЛИ задано условие, которое имеет следующий смысл:
- Если искомый элемент содержится в диапазоне значений, вместо фактического количества вхождений будет возвращено 1;
- Если искомого элемента нет – будет возвращен 0 (нуль).
Полученное значение (количество единиц) суммируется.
В результате получим:
То есть, в указанном массиве содержится 8 уникальных значений.
Скачать пример функции ЧАСТОТА в Excel
Функция ЧАСТОТА в Excel и особенности ее синтаксиса
Данная функция имеет следующую синтаксическую запись:
Описание аргументов функции (оба являются обязательными для заполнения):
- массив_данных – данные в форме массива либо ссылка на диапазон значений, для которых необходимо определить частоты.
- массив_интервалов — данные в формате массива либо ссылка не множество значений, в которые группируются значения первого аргумента данной функции.
Примечания 1:
- Если в качестве аргумента массив_интервалов был передан пустой массив или ссылка на диапазон пустых значений, результатом выполнения функции ЧАСТОТА будет являться число элементов, входящих диапазон данных, которые были переданы в качестве первого аргумента.
- При использовании функции ЧАСТОТА в качестве обычной функции Excel будет возвращено единственное значение, соответствующее первому вхождению в массив_интервалов (то есть, первому критерию поиска частоты вхождения).
- Массив возвращаемых данной функцией элементов содержит на один элемент больше, чем количество элементов, содержащихся в массив_интервалов. Это происходит потому, что функция ЧАСТОТА вычисляет также количество вхождений величин, значения которых превышают верхнюю границу интервалов. Например, в наборе данных 2,7, 10, 13, 18, 4, 33, 26 необходимо найти количество вхождений величин из диапазонов от 1 до 10, от 11 до 20, от 21 до 30 и более 30. Массив интервалов должен содержать только их граничные значения, то есть 10, 20 и 30. Функция может быть записана в следующем виде: =ЧАСТОТА({2;7;10;13;18;4;33;26};{10;20;30}), а результатом ее выполнения будет столбец из четырех ячеек, которые содержат следующие значения: 4,2, 1, 1. Последнее значение соответствует количеству вхождений чисел > 30 в массив_данных. Такое число действительно является единственным – это 33.
- Если в состав массив_данных входят ячейки, содержащие пустые значения или текст, они будут пропущены функцией ЧАСТОТА в процессе вычислений.
Примечания 2:
- Функция может использоваться для выполнения статистического анализа, например, с целью определения наиболее востребованных для покупателей наименований продукции.
- Данная функция должна быть использована как формула массива, поскольку возвращаемые ей данные имеют форму массива. Для выполнения обычных формул после их ввода необходимо нажать кнопку Enter. В данном случае требуется использовать комбинацию клавиш Ctrl+Shift+Enter.
=ЧАСТОТА(массив_данных;массив_интервалов)
В этой статье описаны синтаксис формулы и использование в Microsoft Excel.
Описание
Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.
Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.
Синтаксис
Аргументы функции ДОВЕРИТ описаны ниже.
Альфа — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.
Стандартное_откл — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.
Размер — обязательный аргумент. Размер выборки.
Замечания
Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.
Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.
Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.
Если значение аргумента «размер» не является целым числом, оно усекается.
Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.
Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Подсчет ЧИСЕЛ попадающих в интервал в EXCEL
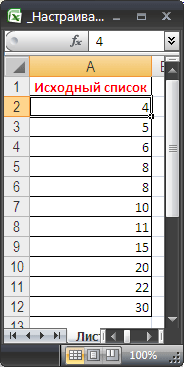
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (См. файл примера ).
Будем подсчитывать значения, попадающие в интервал, например, (4;15]. Причем, границы интервала «включает [ ]» и «не включает ( )» будем выбирать из Выпадающего (раскрывающегося) списка .
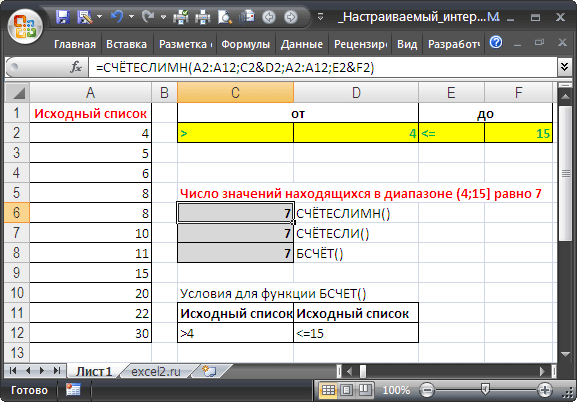
Для настройки границ интервала используем Проверку данных с типом данных Список . В качестве источника укажем для левой границы >;>= и для правой <;<=. Границы интервала будем вводить в диапазон H2 : I3 .
Подсчет можно реализовать множеством формул, приведем несколько:
- = СЧЁТЕСЛИМН(A2:A12;C2&D2;A2:A12;E2&F2)
- = СЧЁТЕСЛИ($A$2:$A$12;C2&D2)-(СЧЁТЗ($A$2:$A$12)-СЧЁТЕСЛИ($A$2:$A$12;E2&F2))
- Формула = БСЧЁТ(A1:A12;A1;H2:I3) требует предварительного создания таблицы с условиями. Заголовки этой таблицы должны в точности совпадать с заголовками исходной таблицы.
СОВЕТ: Более сложные условия подсчета рассмотрены в статье Подсчет значений с множественными критериями (Часть 1. Условие И) .
Функция ДОВЕРИТ и нормальный доверительный интервал в Excel
Функция ДОВЕРИТ в Excel предназначена для определения доверительного интервала для среднего значения, найденного для генеральной совокупности, которая имеет нормальное распределение.
Другими словами, рассматриваемая функция позволяет определить допустимые отклонения для найденного среднего значения с учетом известных уровня значимости (заданная вероятность того, что некоторое значение находится в доверительном интервале) и стандартного отклонения (меры степени разброса значений относительно среднего значения для генеральной совокупности).
Как построить доверительный интервал нормального распределения в Excel
Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.
Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.
Пример расчета доверительного интервала в Excel
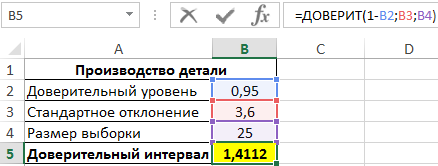
Пример 1. В заводском цехе производят деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины – 3,6 мм. Для контроля качества деталей из партии (генеральная совокупность) делают выборку из 25 деталей. Определить интервал с доверительный уровнем 95%.
Вид таблицы данных:
Для определения доверительного интервала используем функцию:
- 1-B2 – уровень значимости (рассчитан с учетом зависимости от доверительного уровня);
- B3 – значение стандартного отклонения;
- B4 – количество деталей в выборке.
То есть, границы доверительного интервала соответствуют: (Xср-1,4112;Xср+1,4112). Допустим, было определено среднее значение выборки – 199,5 мм. Тогда доверительный интервал примерно определяется как (198,1;200,9), при этом номинальная длина детали (200 мм) находится в доверительном диапазоне, то есть производственный процесс не нарушен.
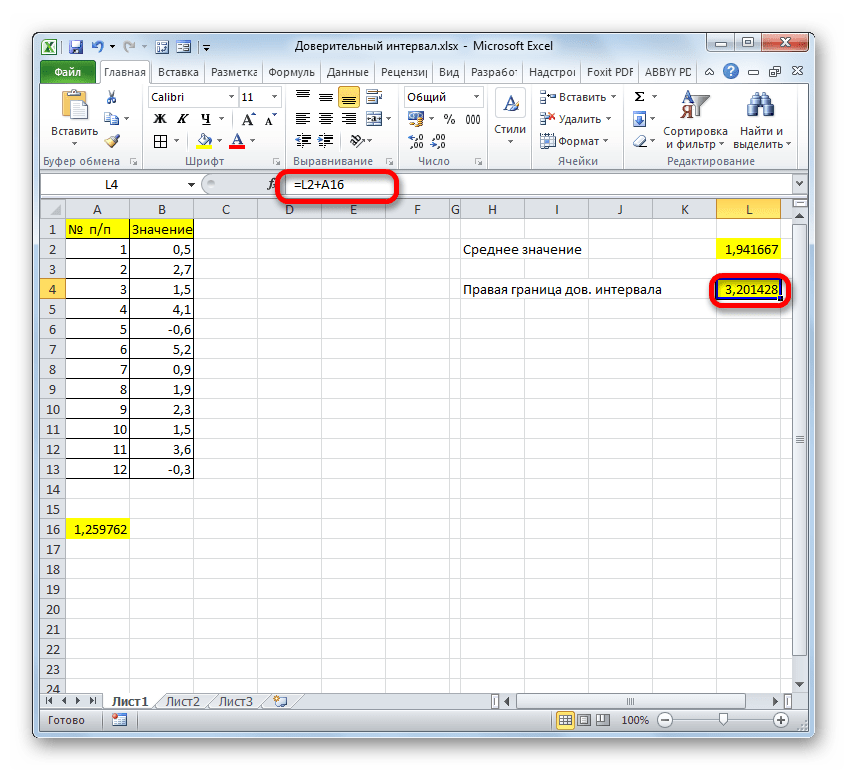
Как найти границы доверительного интервала в Excel
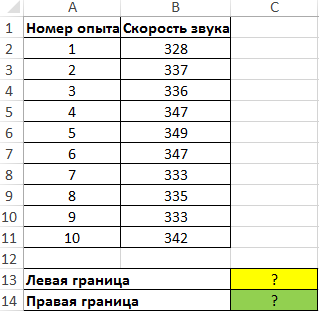
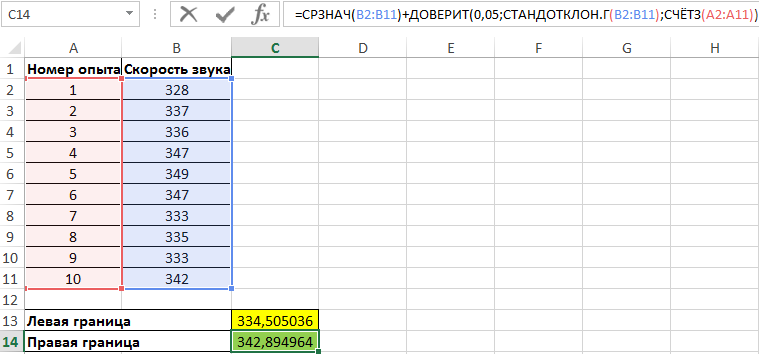
Пример 2. Были проведены опыты по определению скорости распространения звуковой волны в воздухе. Результаты 10 опытов записаны в таблицу. Определить левую и правую границы доверительного интервала для среднего значения.
Вид таблицы данных:
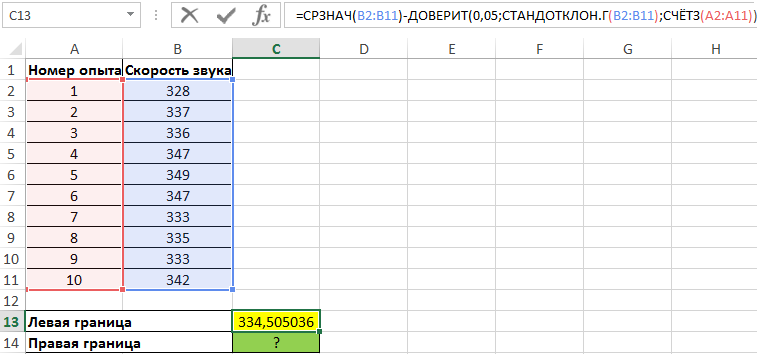
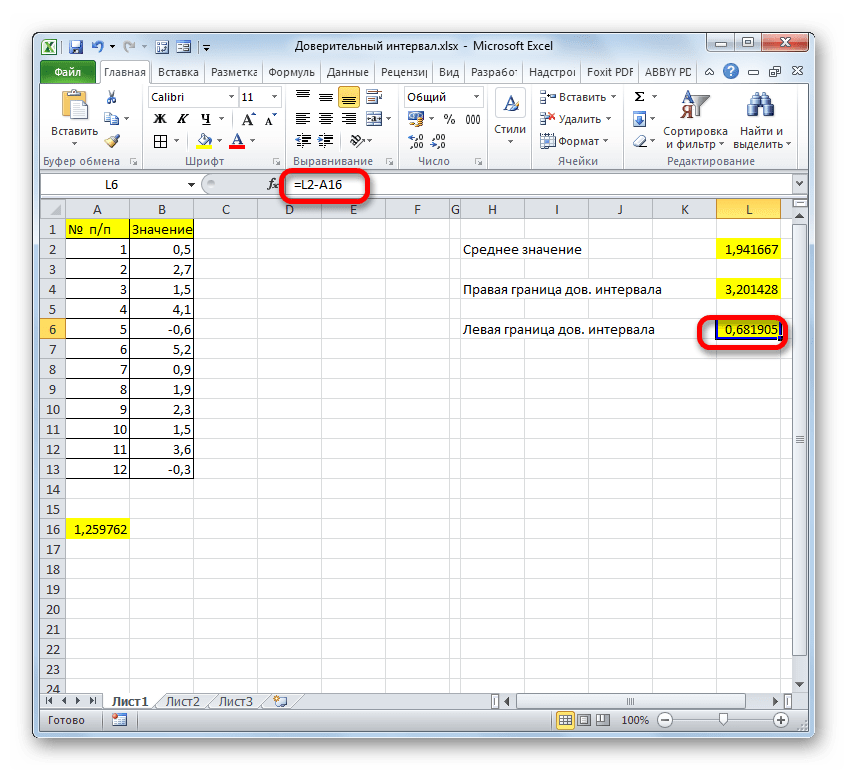
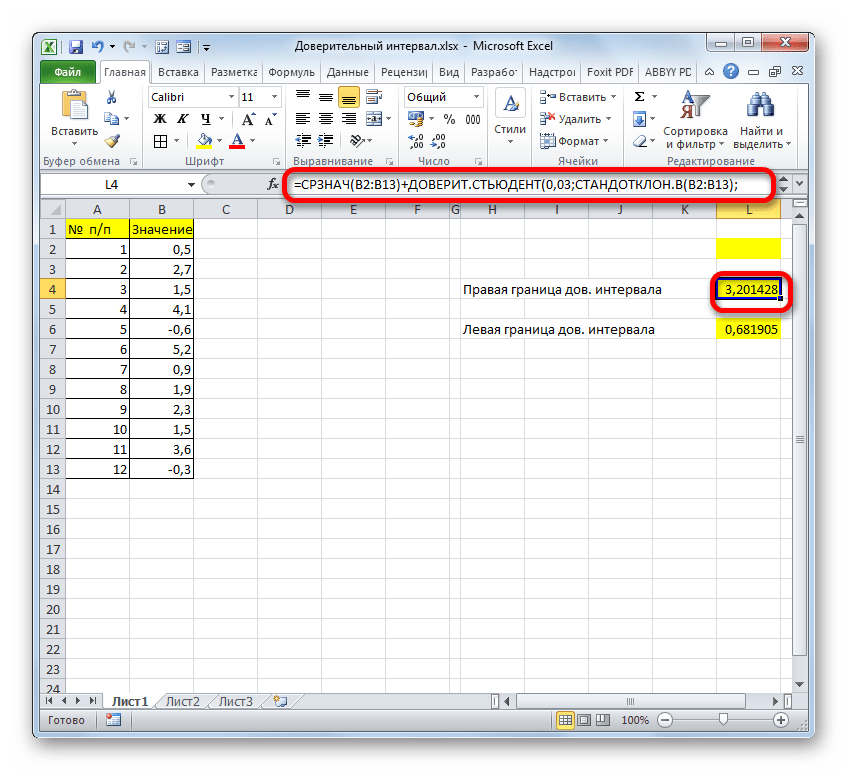
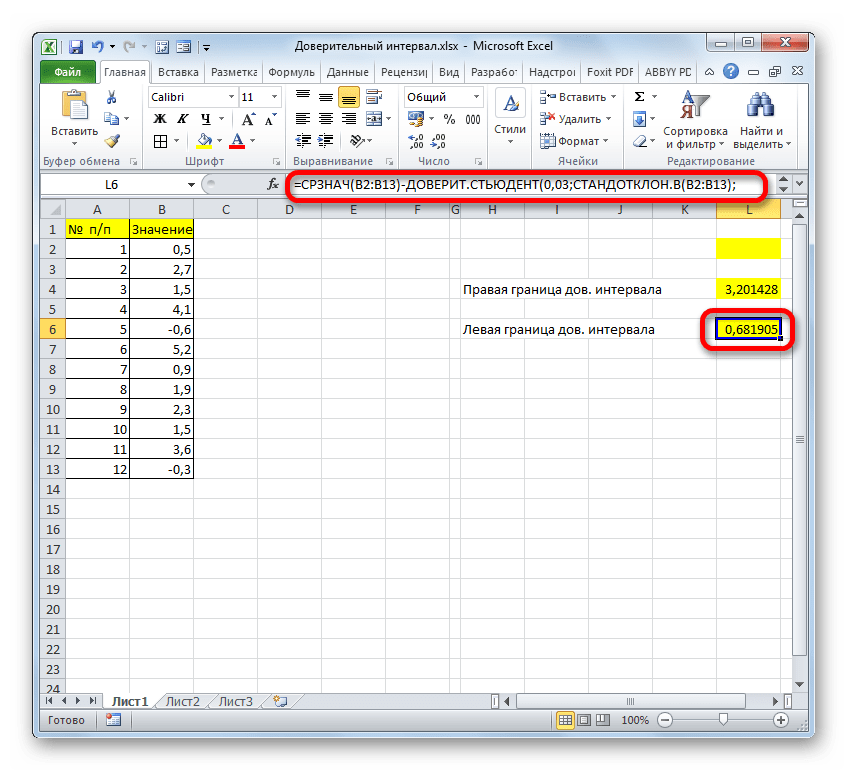
Для нахождения левой границы используем формулу:
В данном случае выборка и генеральная совокупность приняты как имеющиеся данные для 10 проведенных опытов. Среднее выборочное значение рассчитано с помощью функции СРЗНАЧ. Для получения левой границы доверительного интервала из данного значения вычитаем число, полученное в результате выполнения функции ДОВЕРИТ, в которой значение второго аргумента определено с помощью функции СТАНДОТКЛОН.Г, а число опытов – подсчетом количества ячеек функцией СЧЁТЗ.
Поскольку уровень значимости не задан, используем стандартное значение – 0,05.
Правая граница определяется аналогично с разницей в том, что к среднему значению выборки прибавляется результат расчета функции ДОВЕРИТ:
Функция
ЧАСТОТА(
)
, английская версия FREQUENCY()
,
вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией
ЧАСТОТА()
можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См.
Файл примера
)
Синтаксис функции
ЧАСТОТА
(
массив_данных
;
массив_интервалов
)
Массив_данных
— массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов
— массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция
ЧАСТОТА()
вводится как
формула массива
после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши
ENTER
нажать сочетание клавиш
CTRL+SHIFT+ENTER
.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «
массив_интервалов
». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пример
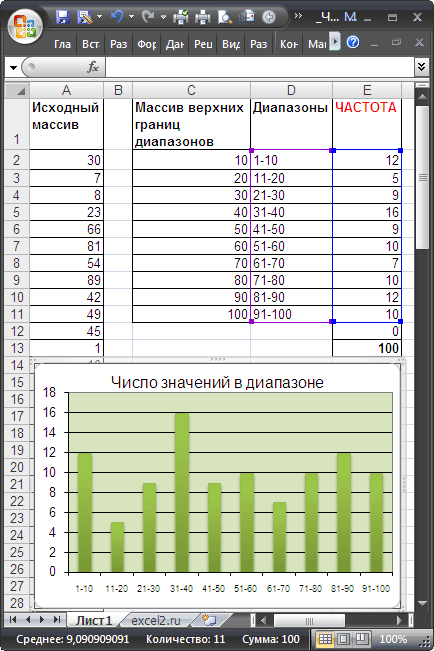
Пусть в диапазоне
А2:А101
имеется исходный массив чисел от 1 до 100.
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; …91-100.
Сформируем столбце
С
массив верхних границ диапазонов (интервалов). Для наглядности в столбце
D
сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; …91-100).
Для ввода формулы выделим диапазон
Е2:Е12
, состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В
Строке формул
введем
=ЧАСТОТА($A$2:$A$101;$C$2:$C$11)
. После ввода формулы необходимо нажать сочетание клавиш
CTRL+SHIFT+ENTER
. Диапазон
Е2:Е12
заполнится значениями:
-
в
Е2
— будет содержаться количество значений из
А2:А101
, которые меньше или равны 10; -
в
Е3
— количество значений из
А2:А101
, которые меньше или равны 20, но больше 10; -
в
Е11
— количество значений из
А2:А101
, которые меньше или равны 100, но больше 90; -
в
Е12
— количество значений из
А2:А101
, которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание
. Функцию
ЧАСТОТА()
можно заменить формулой =
СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104<=C6))
(См.
Файл примера
)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция ЧАСТОТА вычисляет частоту ветвей значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
ЧАСТОТА(массив_данных;массив_интервалов)
Аргументы функции ЧАСТОТА описаны ниже.
-
data_array — обязательный аргумент. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
-
bins_array — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
-
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
-
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Пример
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
На чтение 13 мин Просмотров 6.7к. Опубликовано 31.07.2020
Содержание
- Как построить доверительный интервал нормального распределения в Excel
- Пример расчета доверительного интервала в Excel
- Как найти границы доверительного интервала в Excel
- Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel
- Процедура вычисления
- Способ 1: функция ДОВЕРИТ.НОРМ
- Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
Подсчет чисел, попадающих в интервал – стандартная задача: используйте функцию СЧЕТЕСЛИМН(). Усложним задачу, сделаем интервал легко настраиваемым.
В качестве примера подсчета чисел возьмем список с числовыми значениями от 4 до 30 (См. файл примера ).
Будем подсчитывать значения, попадающие в интервал, например, (4;15]. Причем, границы интервала «включает [ ]» и «не включает ( )» будем выбирать из Выпадающего (раскрывающегося) списка.
Примечание: решение без выбора интервалов = СЧЁТЕСЛИМН(A2:A12;»>»&D2;A2:A12;» Предполагается, что границы интервала введены в ячейки D2 и F2. Эти ячейки не должны быть пустыми, даже если одна из границ =0. Если в диапазоне A2:A12 содержатся числовые значения в текстовом формате, то они будут проигнорированы.
Для настройки границ интервала используем Проверку данных с типом данных Список. В качестве источника укажем для левой границы >;>= и для правой СЧЁТЕСЛИМН(A2:A12;C2&D2;A2:A12;E2&F2)
Функция ДОВЕРИТ в Excel предназначена для определения доверительного интервала для среднего значения, найденного для генеральной совокупности, которая имеет нормальное распределение.
Другими словами, рассматриваемая функция позволяет определить допустимые отклонения для найденного среднего значения с учетом известных уровня значимости (заданная вероятность того, что некоторое значение находится в доверительном интервале) и стандартного отклонения (меры степени разброса значений относительно среднего значения для генеральной совокупности).
Как построить доверительный интервал нормального распределения в Excel
Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.
Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.
Пример расчета доверительного интервала в Excel
Пример 1. В заводском цехе производят деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины – 3,6 мм. Для контроля качества деталей из партии (генеральная совокупность) делают выборку из 25 деталей. Определить интервал с доверительный уровнем 95%.
Вид таблицы данных:
Для определения доверительного интервала используем функцию:
- 1-B2 – уровень значимости (рассчитан с учетом зависимости от доверительного уровня);
- B3 – значение стандартного отклонения;
- B4 – количество деталей в выборке.
То есть, границы доверительного интервала соответствуют: (Xср-1,4112;Xср+1,4112). Допустим, было определено среднее значение выборки – 199,5 мм. Тогда доверительный интервал примерно определяется как (198,1;200,9), при этом номинальная длина детали (200 мм) находится в доверительном диапазоне, то есть производственный процесс не нарушен.
Как найти границы доверительного интервала в Excel
Пример 2. Были проведены опыты по определению скорости распространения звуковой волны в воздухе. Результаты 10 опытов записаны в таблицу. Определить левую и правую границы доверительного интервала для среднего значения.
Вид таблицы данных:
Для нахождения левой границы используем формулу:
В данном случае выборка и генеральная совокупность приняты как имеющиеся данные для 10 проведенных опытов. Среднее выборочное значение рассчитано с помощью функции СРЗНАЧ. Для получения левой границы доверительного интервала из данного значения вычитаем число, полученное в результате выполнения функции ДОВЕРИТ, в которой значение второго аргумента определено с помощью функции СТАНДОТКЛОН.Г, а число опытов – подсчетом количества ячеек функцией СЧЁТЗ.
Поскольку уровень значимости не задан, используем стандартное значение – 0,05.
Правая граница определяется аналогично с разницей в том, что к среднему значению выборки прибавляется результат расчета функции ДОВЕРИТ:
Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel
Функция имеет следующую синтаксическую запись:
- альфа – обязательный, принимает числовое значение, характеризующее уровень значимости – вероятность отклонения нулевой (неверной) гипотезы в том случае, когда она на самом деле верна. Определяется как 1-, где — уровень доверия (вероятность нахождения истинного значения некоторой оцениваемой величины в определенном интервале, называемом доверительным).
- стандартное_откл – обязательный, принимает значение стандартного отклонения величины для генеральной совокупности значений (в Excel предусмотрена функция для определения этой величины — СТАНДОТКЛОН.Г).
- размер – обязательный, принимает числовое значение, характеризующее количество точек данных в анализируемой выборке (ее размер).
- Все аргументы функции должны указываться в виде числовых значений или данных, которые могут быть преобразованы в числа (например, текстовые строки с числами, логические ИСТИНА, ЛОЖЬ). В противном случае результатом выполнения функции ДОВЕРИТ будет код ошибки #ЧИСЛО!
- Аргумент альфа должен быть указан числовым значением из диапазона от 0 до 1 (оба включительно). Иначе функция ДОВЕРИТ вернет код ошибки #ЧИСЛО! Аналогичная ошибка возникает в случаях, когда аргумент стандартное_откл задан числом, взятым из диапазона отрицательных значений или нулем.
- Диапазон допустимых значений для аргумента размер – от 1 до бесконечности со знаком плюс.
Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.
Процедура вычисления
Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.
В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.
Способ 1: функция ДОВЕРИТ.НОРМ
Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.
Его синтаксис выглядит следующим образом:
«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:
«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.
«Размер» — аргумент, определяющий величину выборки.
Все аргументы данного оператора являются обязательными.
Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:
Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.
Граница доверительного интервала определяется при помощи формулы следующего вида:
Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.
Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.
-
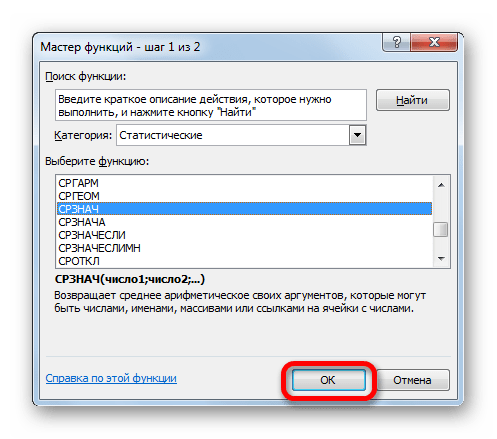
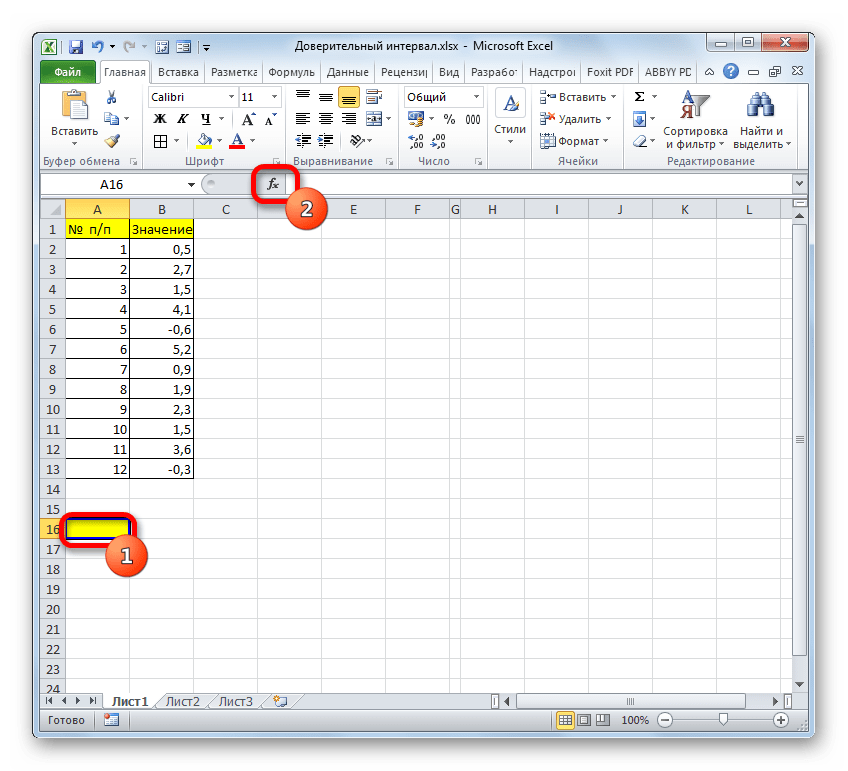
Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».
Появляется Мастер функций. Переходим в категорию «Статистические» и выделяем наименование «ДОВЕРИТ.НОРМ». После этого клацаем по кнопке «OK».
Открывается окошко аргументов. Его поля закономерно соответствуют наименованиям аргументов.
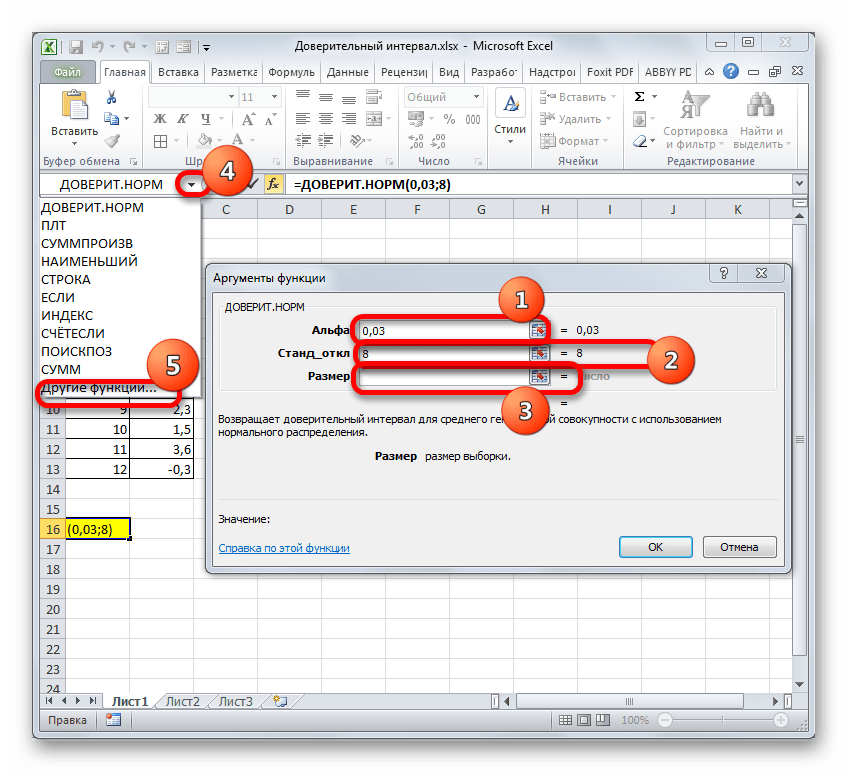
Устанавливаем курсор в первое поле – «Альфа». Тут нам следует указать уровень значимости. Как мы помним, уровень доверия у нас равен 97%. В то же время мы говорили, что он рассчитывается таким путем:
Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:
То есть, подставив значение, получаем:
Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.
Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.
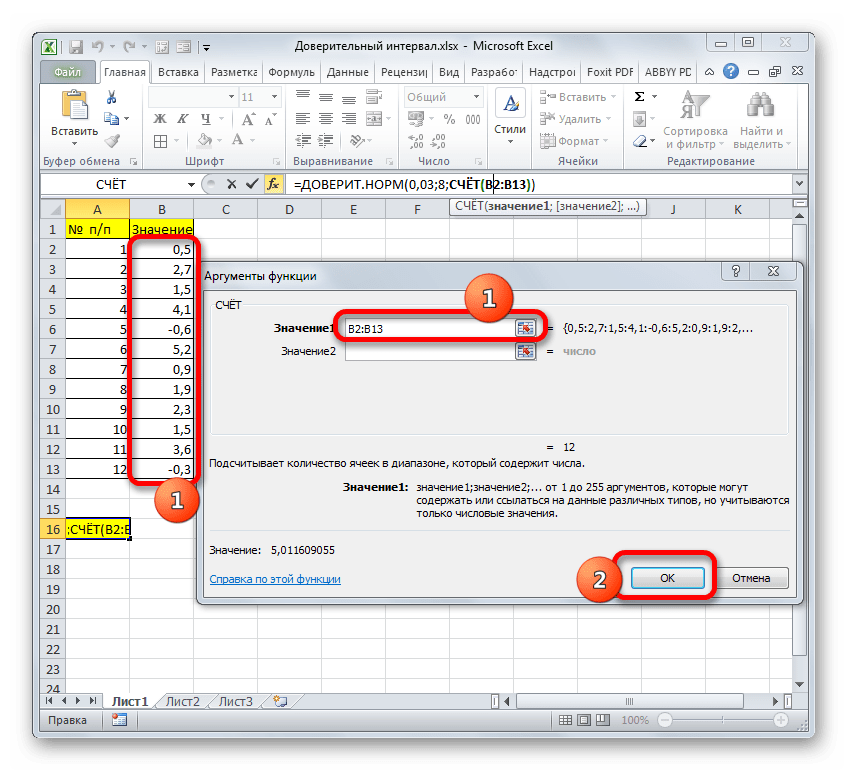
В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.
Появляется список недавно применяемых функций. Если оператор СЧЁТ применялся вами недавно, то он должен быть в этом списке. В таком случае, нужно просто кликнуть по его наименованию. В обратном же случае, если вы его не обнаружите, то переходите по пункту «Другие функции…».
Появляется уже знакомый нам Мастер функций. Опять перемещаемся в группу «Статистические». Выделяем там наименование «СЧЁТ». Клацаем по кнопке «OK».
Появляется окно аргументов вышеуказанного оператора. Данная функция предназначена для того, чтобы вычислять количество ячеек в указанном диапазоне, которые содержат числовые значения. Синтаксис её следующий:
Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.
Устанавливаем курсор в поле «Значение1» и, зажав левую кнопку мыши, выделяем на листе диапазон, который содержит нашу совокупность. Затем его адрес будет отображен в поле. Клацаем по кнопке «OK».
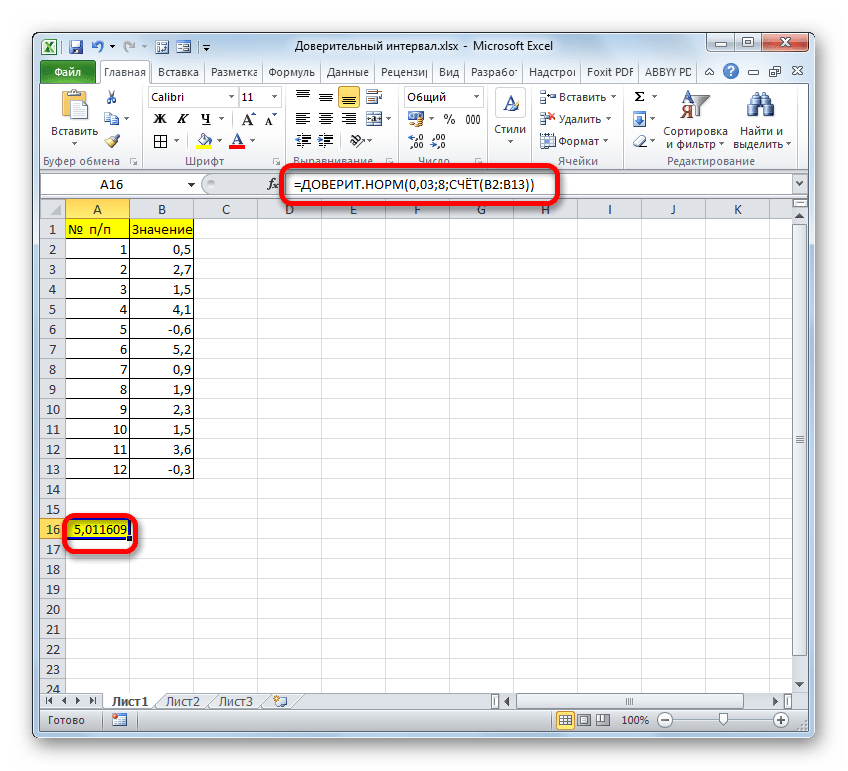
После этого приложение произведет вычисление и выведет результат в ту ячейку, где она находится сама. В нашем конкретном случае формула получилась такого вида:
Общий результат вычислений составил 5,011609.
Но это ещё не все. Как мы помним, граница доверительного интервала вычисляется путем сложения и вычитания от среднего выборочного значения результата вычисления ДОВЕРИТ.НОРМ. Таким способом рассчитывается соответственно правая и левая граница доверительного интервала. Само среднее выборочное значение можно рассчитать при помощи оператора СРЗНАЧ.
Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:
Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.
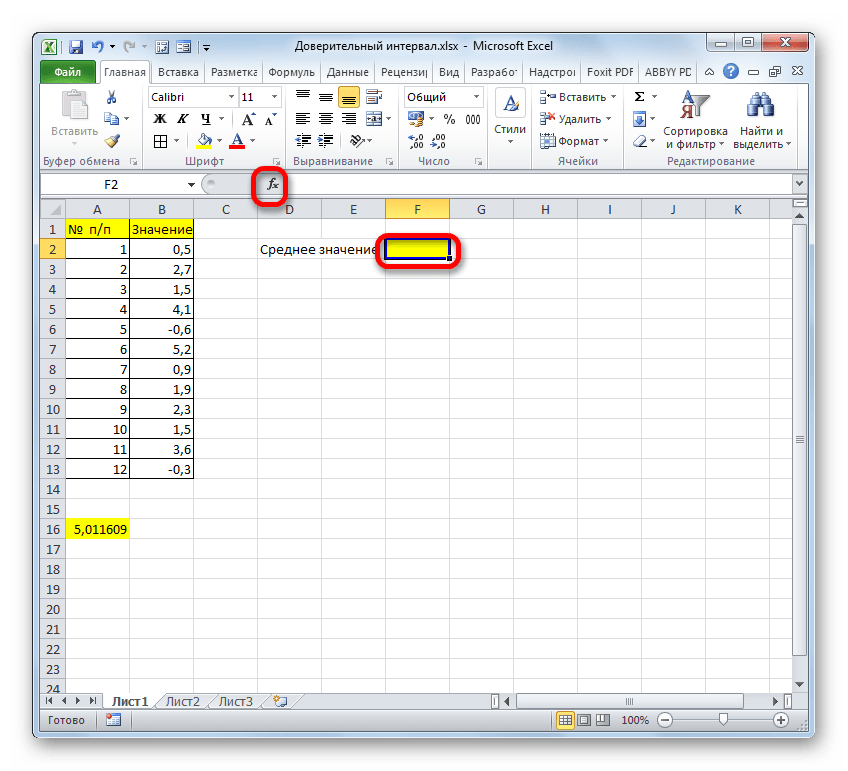
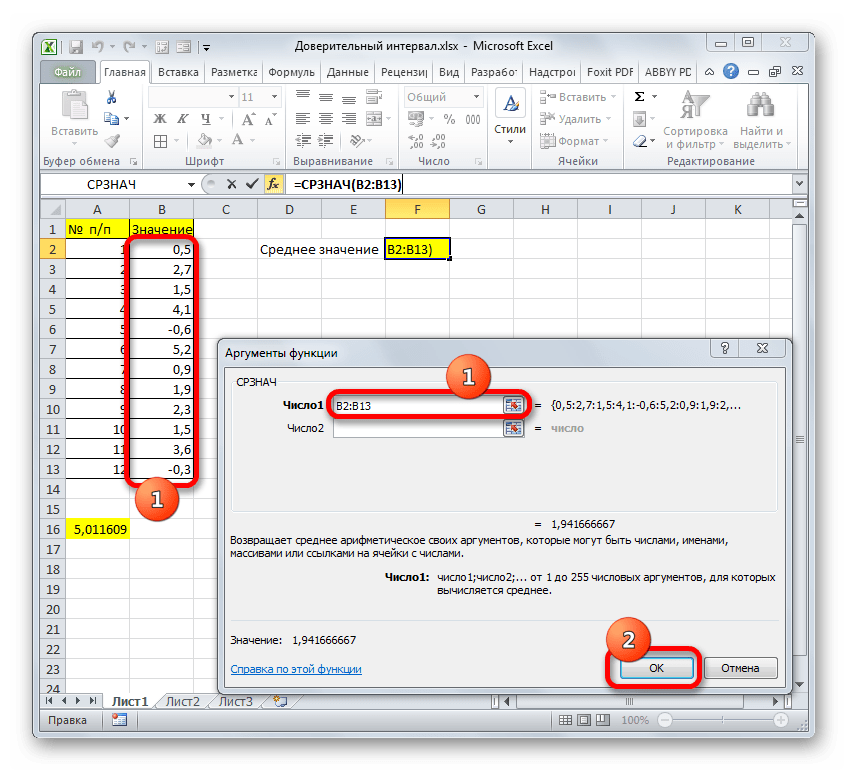
Итак, выделяем ячейку, в которую будет выводиться расчет среднего значения, и щелкаем по кнопке «Вставить функцию».
Открывается Мастер функций. Снова переходим в категорию «Статистические» и выбираем из списка наименование «СРЗНАЧ». Как всегда, клацаем по кнопке «OK».
Запускается окно аргументов. Устанавливаем курсор в поле «Число1» и с зажатой левой кнопкой мыши выделяем весь диапазон значений. После того, как координаты отобразились в поле, клацаем по кнопке «OK».
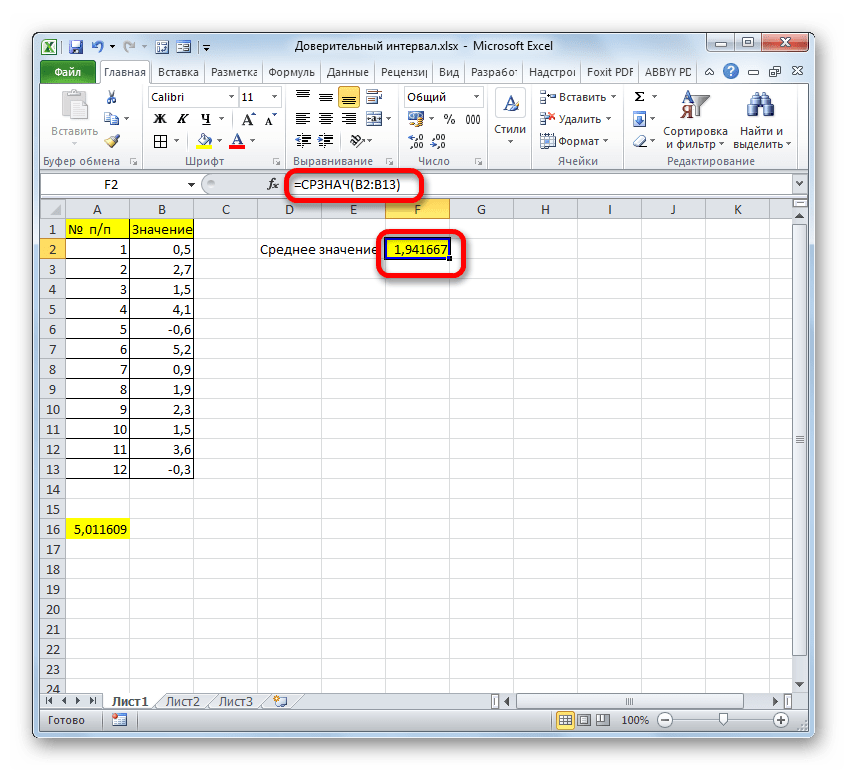
После этого СРЗНАЧ выводит результат расчета в элемент листа.
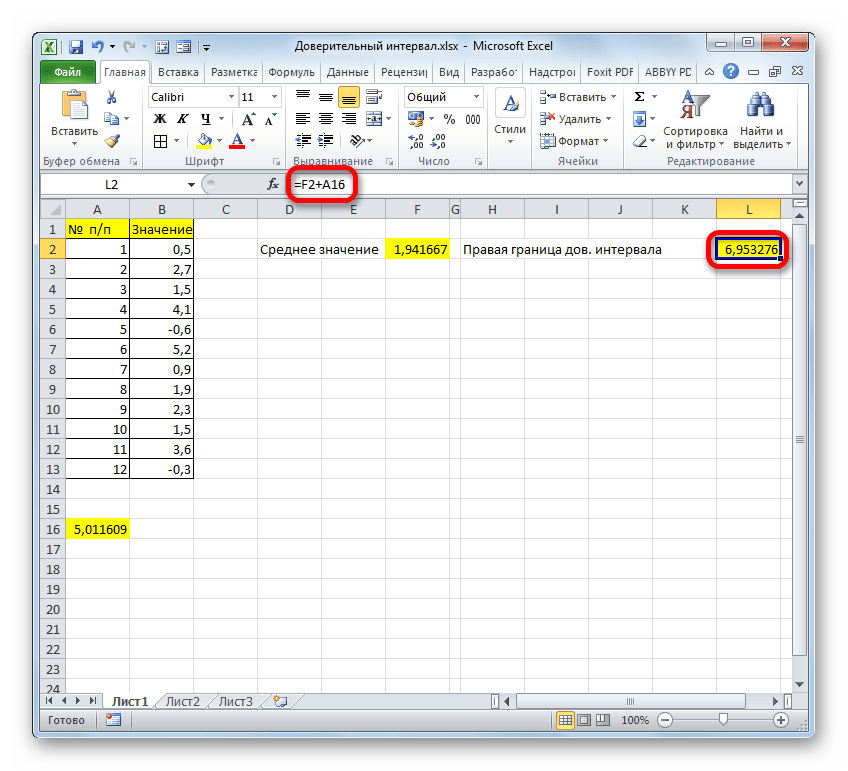
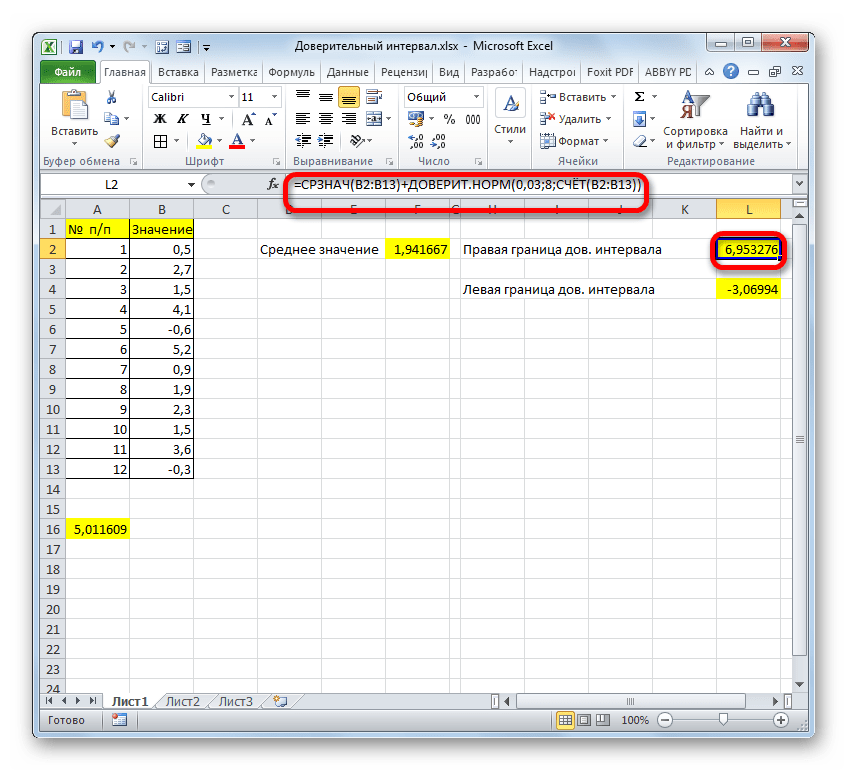
Производим расчет правой границы доверительного интервала. Для этого выделяем отдельную ячейку, ставим знак «=» и складываем содержимое элементов листа, в которых расположены результаты вычислений функций СРЗНАЧ и ДОВЕРИТ.НОРМ. Для того, чтобы выполнить расчет, жмем на клавишу Enter. В нашем случае получилась следующая формула:
Результат вычисления: 6,953276
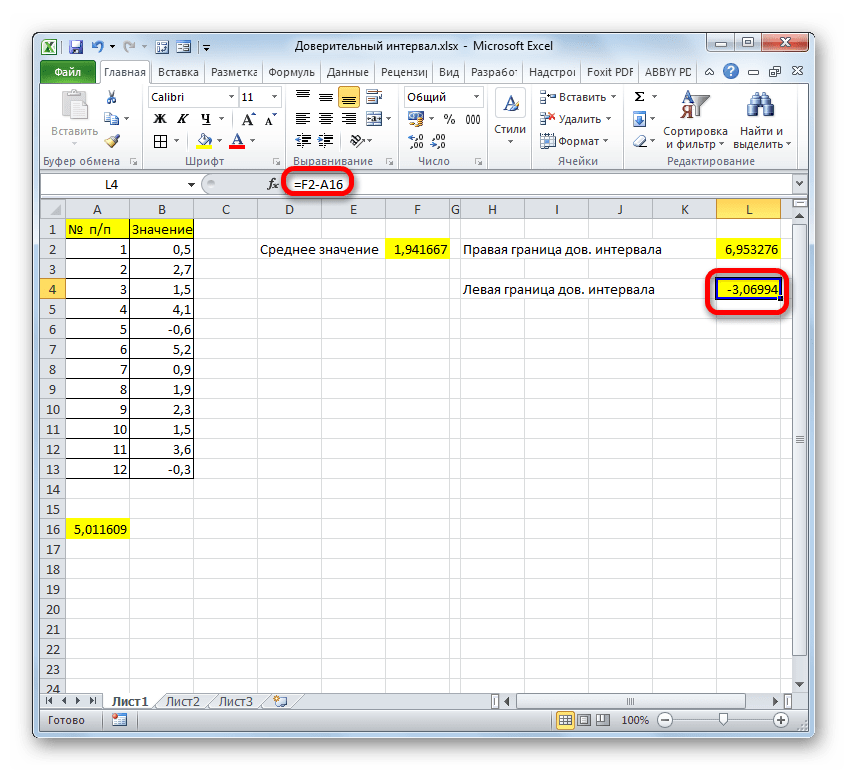
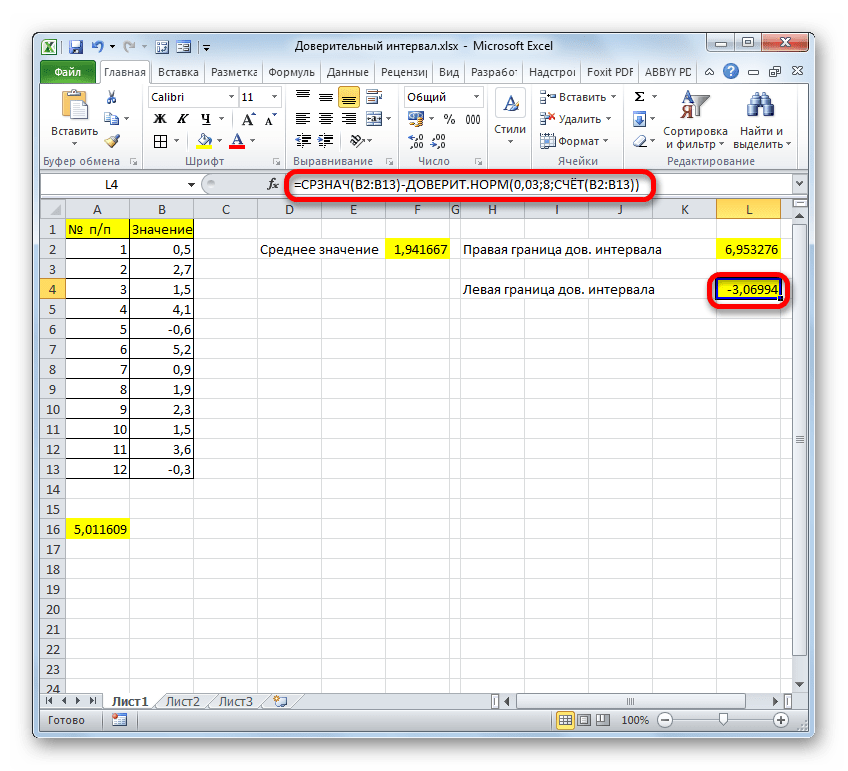
Таким же образом производим вычисление левой границы доверительного интервала, только на этот раз от результата вычисления СРЗНАЧ отнимаем результат вычисления оператора ДОВЕРИТ.НОРМ. Получается формула для нашего примера следующего типа:
Результат вычисления: -3,06994
Мы попытались подробно описать все действия по вычислению доверительного интервала, поэтому детально расписали каждую формулу. Но можно все действия соединить в одной формуле. Вычисление правой границы доверительного интервала можно записать так:
Аналогичное вычисление левой границы будет выглядеть так:
Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
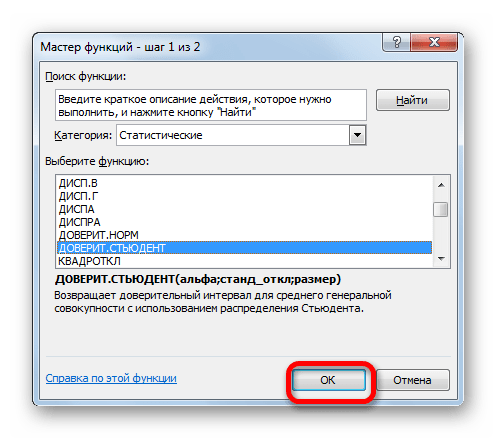
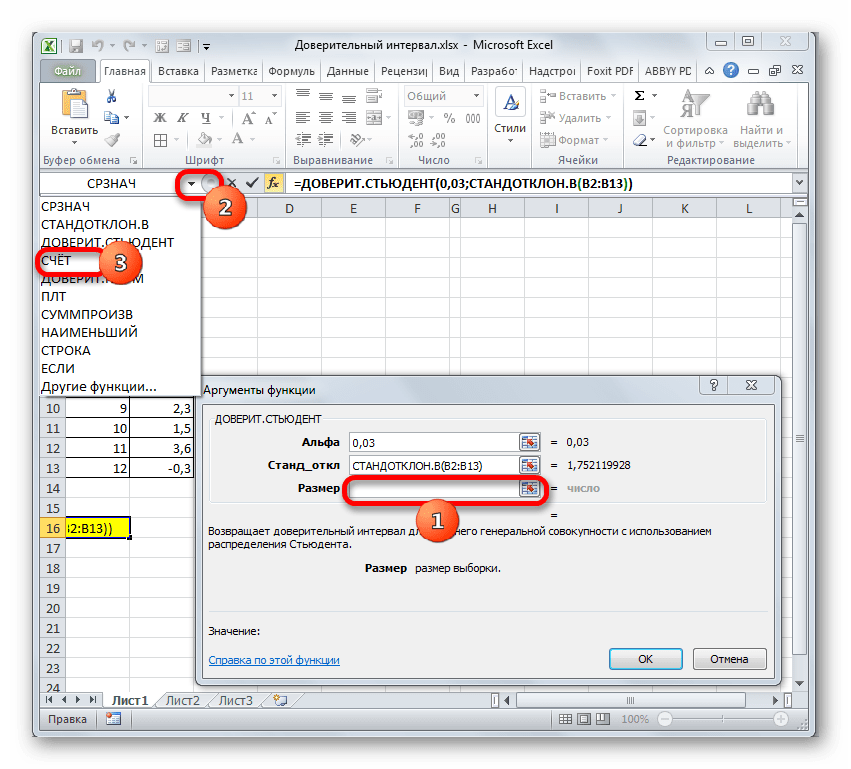
Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:
Как видим, наименования операторов и в этом случае остались неизменными.
Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.
-
Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».
В открывшемся Мастере функций переходим в категорию «Статистические». Выбираем наименование «ДОВЕРИТ.СТЮДЕНТ». Клацаем по кнопке «OK».
Производится запуск окна аргументов указанного оператора.
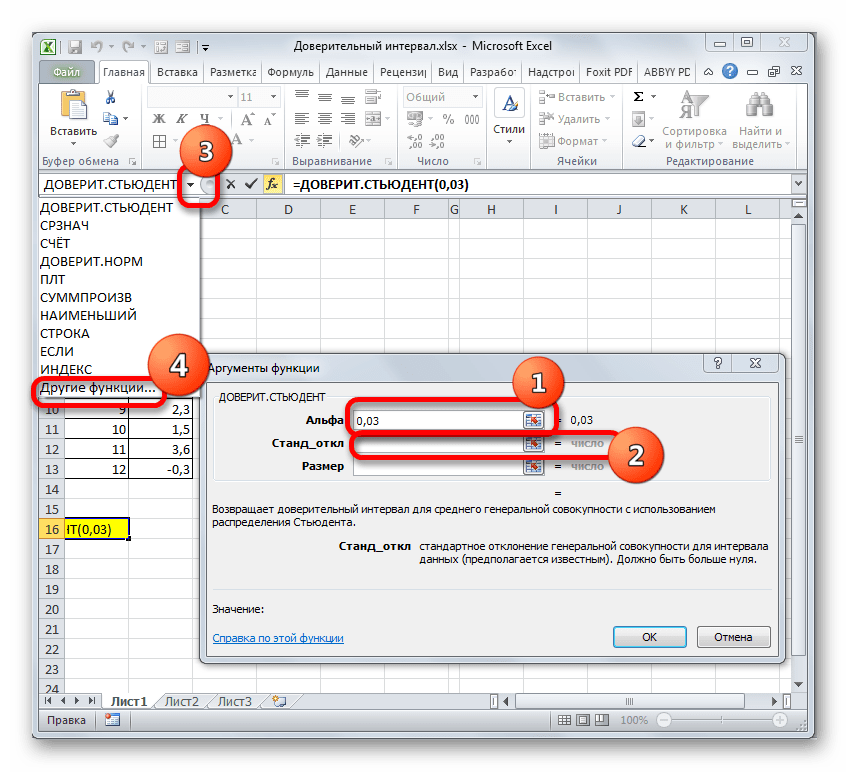
В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.
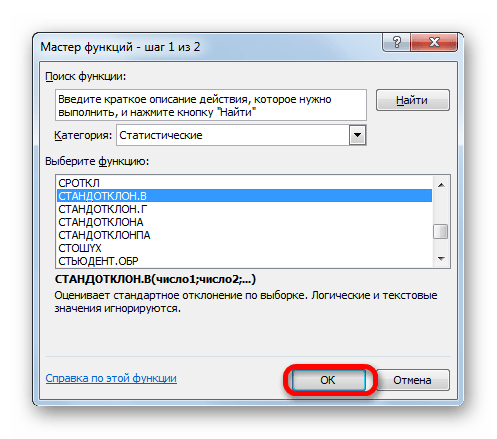
После этого устанавливаем курсор в поле «Стандартное отклонение». На этот раз данный показатель нам неизвестен и его требуется рассчитать. Делается это при помощи специальной функции – СТАНДОТКЛОН.В. Чтобы вызвать окно данного оператора, кликаем по треугольнику слева от строки формул. Если в открывшемся списке не находим нужного наименования, то переходим по пункту «Другие функции…».
Запускается Мастер функций. Перемещаемся в категорию «Статистические» и отмечаем в ней наименование «СТАНДОТКЛОН.В». Затем клацаем по кнопке «OK».
Открывается окно аргументов. Задачей оператора СТАНДОТКЛОН.В является определение стандартного отклонения при выборке. Его синтаксис выглядит так:
Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.
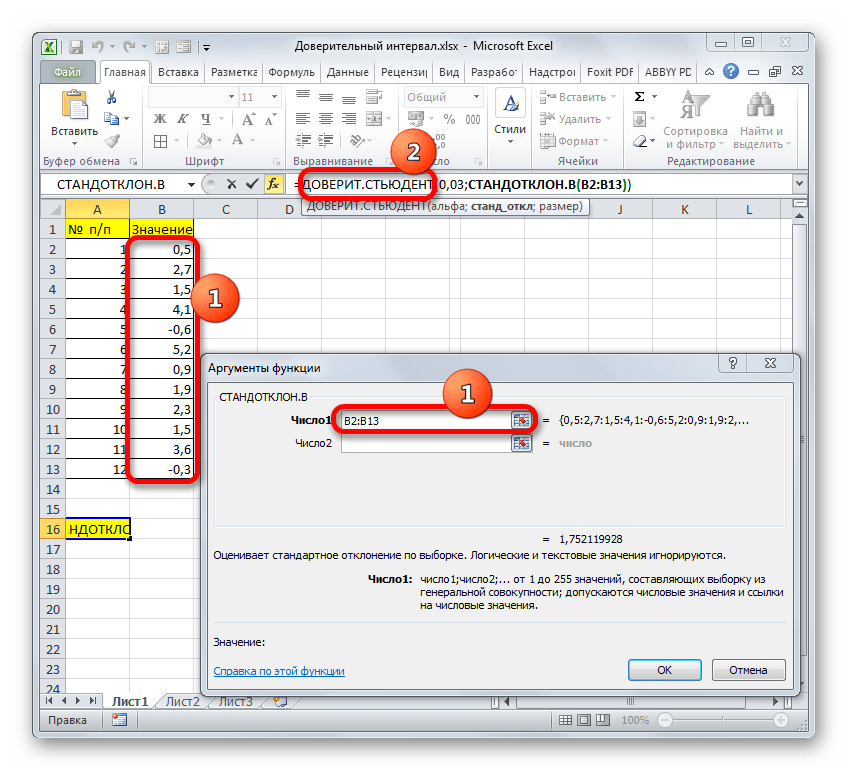
Устанавливаем курсор в поле «Число1» и, как всегда, зажав левую кнопку мыши, выделяем совокупность. После того, как координаты попали в поле, не спешим жать на кнопку «OK», так как результат получится некорректным. Прежде нам нужно вернуться к окну аргументов оператора ДОВЕРИТ.СТЮДЕНТ, чтобы внести последний аргумент. Для этого кликаем по соответствующему наименованию в строке формул.
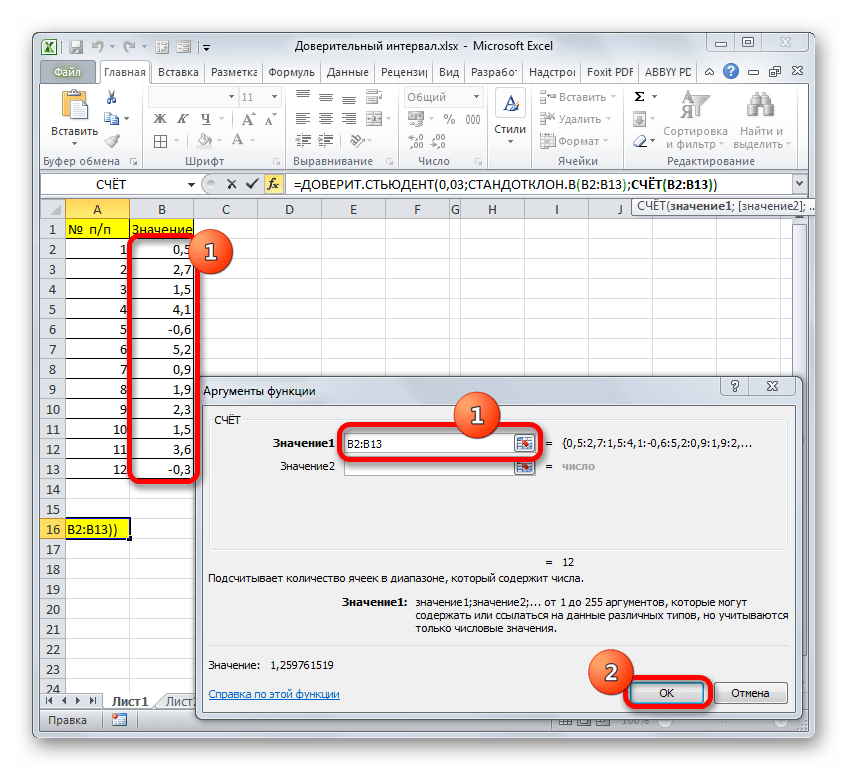
Снова открывается окно аргументов уже знакомой функции. Устанавливаем курсор в поле «Размер». Опять жмем на уже знакомый нам треугольник для перехода к выбору операторов. Как вы поняли, нам нужно наименование «СЧЁТ». Так как мы использовали данную функцию при вычислениях в предыдущем способе, в данном списке она присутствует, так что просто щелкаем по ней. Если же вы её не обнаружите, то действуйте по алгоритму, описанному в первом способе.
Попав в окно аргументов СЧЁТ, ставим курсор в поле «Число1» и с зажатой кнопкой мыши выделяем совокупность. Затем клацаем по кнопке «OK».
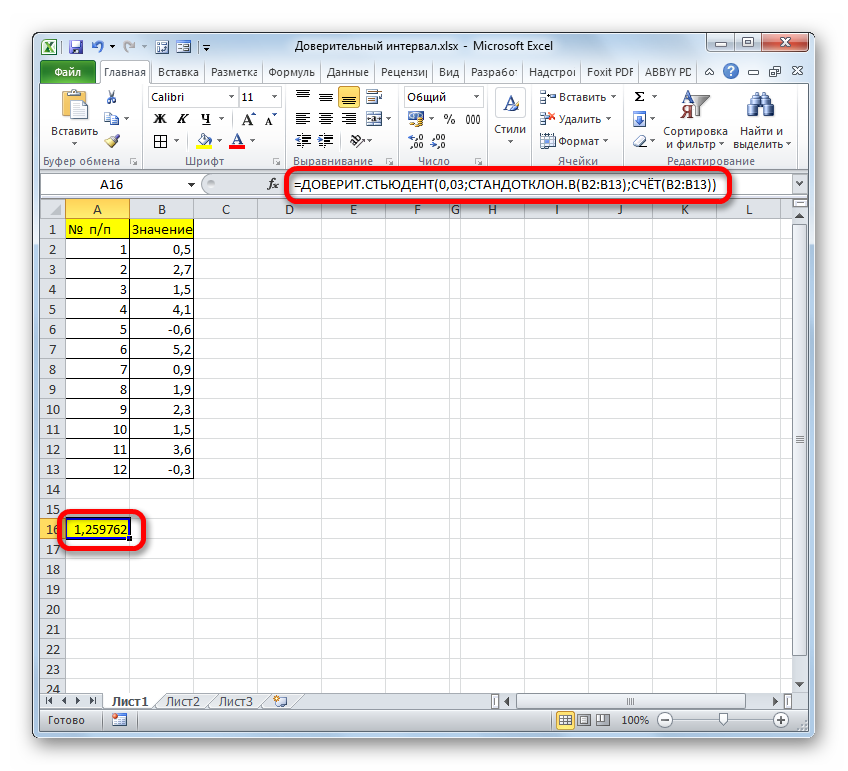
После этого программа производит расчет и выводит значение доверительного интервала.
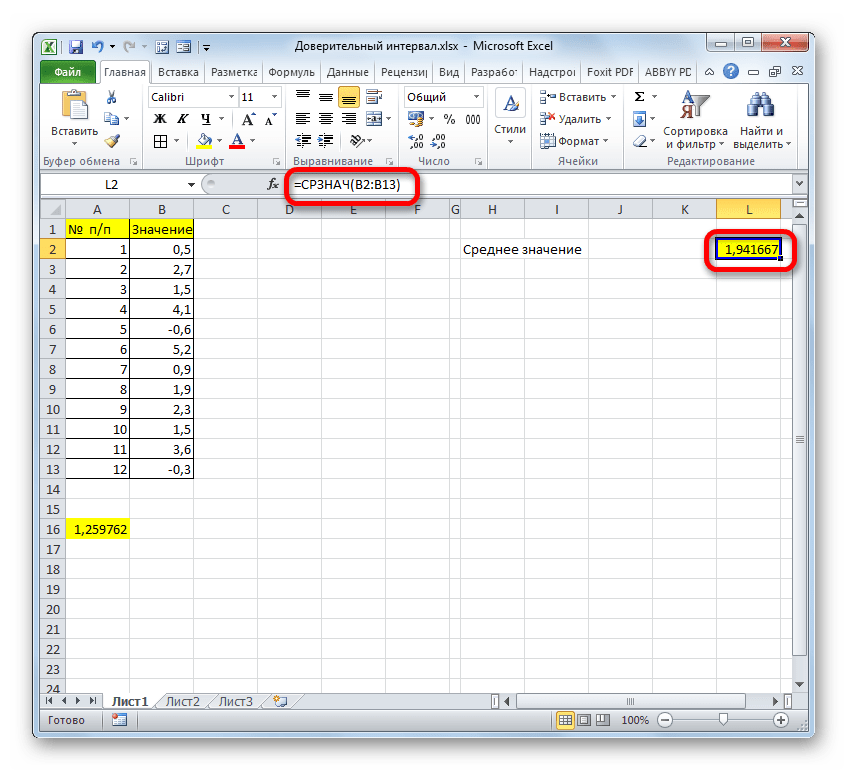
Для определения границ нам опять нужно будет рассчитать среднее значение выборки. Но, учитывая то, что алгоритм расчета при помощи формулы СРЗНАЧ тот же, что и в предыдущем способе, и даже результат не изменился, не будем на этом подробно останавливаться второй раз.
Сложив результаты вычисления СРЗНАЧ и ДОВЕРИТ.СТЮДЕНТ, получаем правую границу доверительного интервала.
Отняв от результатов расчета оператора СРЗНАЧ результат расчета ДОВЕРИТ.СТЮДЕНТ, имеем левую границу доверительного интервала.
Если расчет записать одной формулой, то вычисление правой границы в нашем случае будет выглядеть так:
Соответственно, формула расчета левой границы будет выглядеть так:
Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.
Отблагодарите автора, поделитесь статьей в социальных сетях.
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:
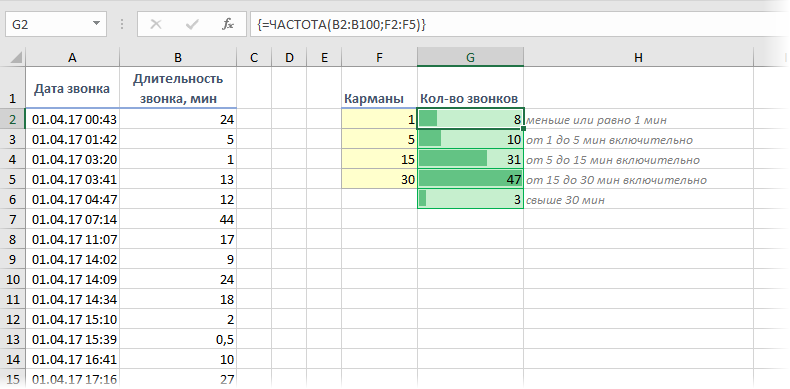
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY). Ее синтаксис прост:
=ЧАСТОТА(Данные; Карманы)
где
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
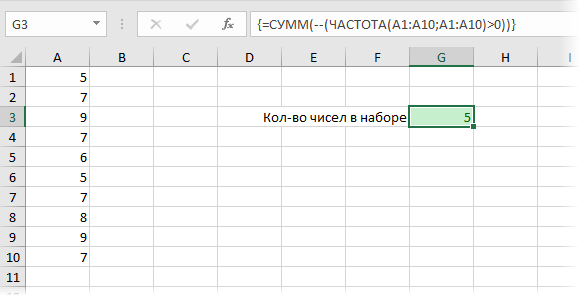
Ссылки по теме
- Как подсчитать количество уникальных элементов в списке
- Как сделать список без повторений
- Частотный анализ данных с помощью сводных таблиц и формул
Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL
Функция ЧАСТОТА( ) , английская версия FREQUENCY(), вычисляет частоту попадания значений в заданные пользователем интервалы и возвращает соответствующий массив чисел.
Функцией ЧАСТОТА() можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в определенные интервалы (См. Файл примера )
Синтаксис функции
ЧАСТОТА(массив_данных;массив_интервалов)
Массив_данных — массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты.
Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных».
Функция ЧАСТОТА() вводится как формула массива после выделения диапазона смежных ячеек, в которые требуется вернуть полученный массив распределения (частот). Т.е. после ввода формулы необходимо вместо нажатия клавиши ENTER нажать сочетание клавиш CTRL+SHIFT+ENTER.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (см. пример ниже).
Пусть в диапазоне А2:А101 имеется исходный массив чисел от 1 до 100.
Подсчитаем количество чисел, попадающих в интервалы 1-10; 11-20; . 91-100.
Сформируем столбце С массив верхних границ диапазонов (интервалов). Для наглядности в столбце D сформируем текстовые значения соответствующие границам интервалов (1-10; 11-20; . 91-100).
Для ввода формулы выделим диапазон Е2:Е12, состоящий из 11 ячеек (на 1 больше, чем число верхних границ интервалов). В Строке формул введем =ЧАСТОТА($A$2:$A$101;$C$2:$C$11) . После ввода формулы необходимо нажать сочетание клавиш CTRL+SHIFT+ENTER. Диапазон Е2:Е12 заполнится значениями:
- в Е2 — будет содержаться количество значений из А2:А101, которые меньше или равны 10;
- в Е3 — количество значений из А2:А101, которые меньше или равны 20, но больше 10;
- в Е11 — количество значений из А2:А101, которые меньше или равны 100, но больше 90;
- в Е12 — количество значений из А2:А101, которые больше 100 (таких нет, т.к. исходный массив содержит числа от 1 до 100).
Примечание. Функцию ЧАСТОТА() можно заменить формулой = СУММПРОИЗВ(($A$5:$A$104>C5)*($A$5:$A$104 Похожие задачи
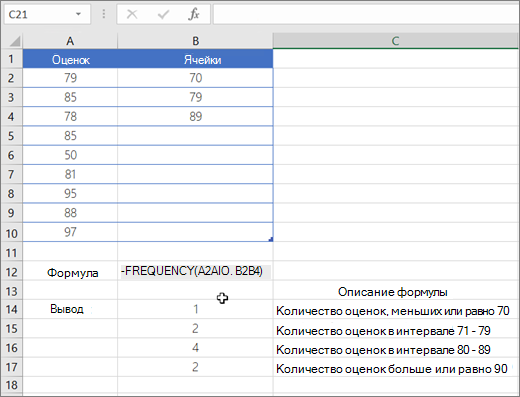
Глава 16. Функция массива ЧАСТОТА
Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Знакомство с функциями массива началось в главе 9. Мы узнали о функциях: ТРАНСП, МОДА.НСК и ТЕНДЕНЦИЯ. Настоящая заметка знакомит с четвертой функцией массива – ЧАСТОТА. Эта функция очень простая, но весьма мощная и универсальная. Она находит массу применений. Основная задача функции ЧАСТОТА – подсчитать, сколько чисел попадают в диапазон (рис. 16.1).
Рис. 16.1. Функция ЧАСТОТА подсчитывает, сколько результатов попали в тот или иной диапазон; диапазоны в D5:D10 не являются частью формулы; они показаны для иллюстрации
Скачать заметку в формате Word или pdf, примеры в формате Excel
Функция ЧАСТОТА в диапазоне Е5:Е10 введена с помощью Ctrl+Shift+Enter. Функция возвращает вертикальный массив, показывающий число вхождений результатов гонки в каждую категорию (диапазон). Например, в диапазон от 45 до 50 с попало 5 результатов. Функция содержит два аргумента: массив_данных и массив_интервалов (массив_карманов). Обратите внимание, что функция возвращает значений на одно больше чем массив_интервалов. Экстра-значение нужно на случай, если вы не предоставите «правильное» максимальное значение в массиве интервалов, и найдутся значения, выходящие за верхнюю границу максимального диапазона. Обратите внимание:
- Первый диапазон включает все значения, которые меньше или равны первой границе.
- Далее диапазоны формируются так, что нижняя граница не входит в диапазон, а верхняя – входит.
- Последний диапазон включает все значения, которые больше, чем последняя граница.
- Функция возвращает вертикальный массив. Если вам нужен горизонтальный массив, используйте функцию ТРАНСП (рис. 16.2).
- Если аргумент массив_карманов содержит N значений, диапазон введения функции ЧАСТОТА должен содержать N+1 ячеек.
- Функция ЧАСТОТА игнорирует пустые ячейки и текст.
- Если массив_интервалов содержит дубли, во все диапазоны-дубли, кроме первого, функция вернет 0.
- После того, как функция введена с помощью Ctrl+Shift+Enter, результирующий массив становится единым блоком и отдельные ячейки нельзя ни удалить, ни отредактировать. Но вы можете удалить все значения.
- Функция ЧАСТОТА может использоваться внутри больших формул массивов, возвращая вертикальный массив.
Рис. 16.2. Используйте функцию массива ТРАНСП, если нужно получить горизонтальный массив
Сравнение функций СЧЁТЕСЛИ, СЧЁТЕСЛИМН и ЧАСТОТА
Когда ваша цель – подсчет числа вхождений между нижней и верхней границами, вы должны рассмотреть, будут ли значения границ входить в диапазоны. Если у вас есть категории, подобные показанным на рис. 16.3, использовать функцию ЧАСТОТА гораздо проще, чем функции СЧЁТЕСЛИ или СЧЁТЕСЛИМН. Вы видите, что вам придется создать три разные формулы, если вы все же решите использовать СЧЁТЕСЛИ или СЧЁТЕСЛИМН вместо функции ЧАСТОТА. В данном примере ваш выбор однозначен – функция ЧАСТОТА.
Рис. 16.3. Функции СЧЁТЕСЛИ и СЧЁТЕСЛИМН сложнее, чем ЧАСТОТА; Чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Однако, если диапазоны включает нижнюю границу, но не верхнюю (рис. 16.4) функция ЧАСТОТА не подойдет. Кроме того, вы можете предусмотреть введение нижней и верхней границ для всех диапазонов, так что формулы примут одинаковый вид. В этом примере, вы отметаете функцию ЧАСТОТА, и скорее всего, предпочтете СЧЁТЕСЛИМН.
Рис. 16.4. СЧЁТЕСЛИ и СЧЁТЕСЛИМН более гибки по сравнению с функцией ЧАСТОТА при задании различных условий по вхождению границ в диапазоны
В следующей главе вы используете полученные знания о функции ЧАСТОТА для построения формул подсчета уникальных элементов в списке.
Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы — диапазон с границами интервалов, попадание в которые нас интересует
- Данные — диапазон с исходными числовыми значениями, которые мы анализируем
Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Функция ЧАСТОТА
Функция частота Вычисляет частоту возникновения значений в диапазоне значений и возвращает вертикальный массив чисел. Функцией ЧАСТОТА можно воспользоваться, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, ее необходимо вводить как формулу массива.
Аргументы функции ЧАСТОТА описаны ниже.
дата_аррай Обязательный. Массив или ссылка на множество значений, для которых вычисляются частоты. Если аргумент «массив_данных» не содержит значений, функция ЧАСТОТА возвращает массив нулей.
бинс_аррай — обязательный аргумент. Массив или ссылка на множество интервалов, в которые группируются значения аргумента «массив_данных». Если аргумент «массив_интервалов» не содержит значений, функция ЧАСТОТА возвращает количество элементов в аргументе «массив_данных».
Примечание: Если у вас установлена текущая версия Office 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве «массив_интервалов». Дополнительный элемент в возвращаемом массиве содержит количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения. Например, при подсчете трех диапазонов значений (интервалов), введенных в три ячейки, убедитесь в том, что функция ЧАСТОТА возвращает значения в четырех ячейках. Дополнительная ячейка возвращает число значений в аргументе «массив_данных», превышающих значение верхней границы третьего интервала.
Функция ЧАСТОТА пропускает пустые ячейки и текст.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
KT Богомолов / МУ / ЗАДАНИЕ_1_СТАТИСТИКА / Дополнительные материалы / Построение гистограмм в Excel_2014
Построение гистограмм в Microsoft Excel
Перед построением гистограммы выполняется группировка данных по близким признакам. При группировании по количественному признаку все множество значений признака делится на
Для определения оптимального количества интервалов может быть использована формула Стерджесса:
n = 1 + (3,322 × lgN )
где N — количество наблюдений. В этом случае величина интервала:
h = ( V max — V min )/ n
Поскольку количество групп не может быть дробным числом, то полученную по этой формуле величину округляют до целого большего числа.
Нижнюю границу первого интервала принимают равной минимальному значению x min . Верхняя граница первого интервала соответствует значению ( x min + h ). Для последующих групп
границы определяются аналогично, то есть последовательно прибавляется величина интервала h .
В Excel для построения гистограмм используются статистическая функция ЧАСТОТА в сочетании с мастером построения обычных диаграмм и процедура Гистограмма из пакета анализа .
Функция ЧАСТОТА (массив_данных, двоичный_массив) вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр, где
• Массив_данных — массив исходных данных, для которых вычисляются частоты;
• Массив_интервалов — это массив интервалов, по которым группируются значения выборки .
Перед вызовом функции ЧАСТОТА необходимо выделить столбец c числом ячеек, равным числу интервалов n , в который будут выведены результаты выполнения функции.
Вызвать Мастер функций (кнопка f x ):
и функцию ЧАСТОТА .
В поле Массив_данных ввести диапазон данных наблюдений А3:А102 (с листа ‘Расчетные данные’) . В поле Массив_интервалов ввести диапазон интервалов с того же листа ([‘Расчетные данные’!F16:F23] – в данном примере).
При завершении ввода данных нажать комбинацию клавиш Ctrl+Shift+Enter.
В предварительно выделенном столбце (C5:C12 – в данном примере) должен появиться массив
Столбец Накопленные частоты получается последовательным суммированием относительных частот (в процентном формате) в направлении от первого интервала к последнему.
В завершении с помощью Мастера диаграмм строится диаграмма абсолютных и накопленных частот с выбором типа диаграммы соотвественно гистограмма и график.
Для автоматизированного построения гистограммы средствами Excel необходимо обратиться к меню « Сервис Анализ данных» . (Excel 2003) или на вкладке Данные выбрать Анализ данных
(Excel 2007. 2010):
В появившемся списке выбрать инструмент Гистограмма и щелкнуть на кнопке ОК. Появится окно гистограммы, где задаются следующие параметры:
Входной интервал :– адреса ячеек, содержащие выборочные данные.
Интервал карманов : (необязательный параметр) – адреса ячеек, содержащие границы интервалов. Это поле предлагается оставить пустым, предоставив Excel самому вычислить границы интервалов (карманов – в терминах Excel).
Метки – флажок, включаемый, если первая строка во входных данных содержит заголовки. Если заголовки отсутствуют, то флажок следует выключить.
Выходной интервал: / Новый рабочий лист: / Новая рабочая книга.
Включенный переключатель Выходной интервал требует ввода адреса верхней ячейки, начиная с которой будут размещаться вычисленные относительные частоты j .
В положении переключателя Новый рабочий лист: открывается новый лист, в котором начиная с ячейки А1 размещаются частности j .
В положении переключателя Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 размещаются частности j .
Парето ( отсортированная гистограмма ) – устанавливается, чтобы представить j в порядке их убывания. Если параметр выключен, то j приводятся в порядке следования интервалов.
Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных относительных частот (аналог значений столбца Накопленные частоты ).
Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем частоты.
Как правило, гистограммы изображаются в виде смежных прямоугольных областей. Поэтому столбики гистограммы следует расширить до соприкосновения друг с другом. Для этого необходимо щелкнуть мышью на диаграмме, далее на панель инструментов Диаграмма , раскрыть список инструментов и выбрать элемент Ряд ‘Частота’ , после чего щелкнуть на кнопке Формат ряда . В появившемся одноименном диалоговом окне необходимо активизировать закладку Параметры и в поле Ширина зазора установить значение 0 ((Excel 2003):
В Excel 2007. 2010 встать на любой столбик гистограммы и правой кнопкой мыши выбрать
Формат ряда данных:
Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты.
В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее; стандартное_откл; интегральная) , где:
х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения;
интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения.
Для получения абсолютных значений плотностей распределения (теоретических частот) достаточно найденные значения вероятности умножить на величину интервала h и количество наблюдений N = 100 по каждой строке.
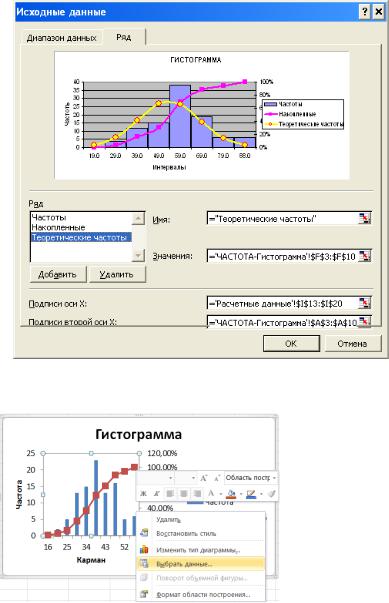
Для завершения выполнения задания необходимо внести полученные значения теоретических частот на рисунок с гистограммой, добавив ряд в закладке Исходные данные и выбрав тип диаграммы
– график ((Excel 2003):
В Excel 2007. 2010 находясь в обласи гистограммы по правой кнопке мыши выбрать Выбрать данные (или по одноименной кнопке на вкладке Конструктор ):
и в появившемся окне провести манипуляции с вводом нового ряда «Теоретические частоты»: