Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Вопросы и ответы
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
f(x) = e^n,
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
=EXP(число)
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
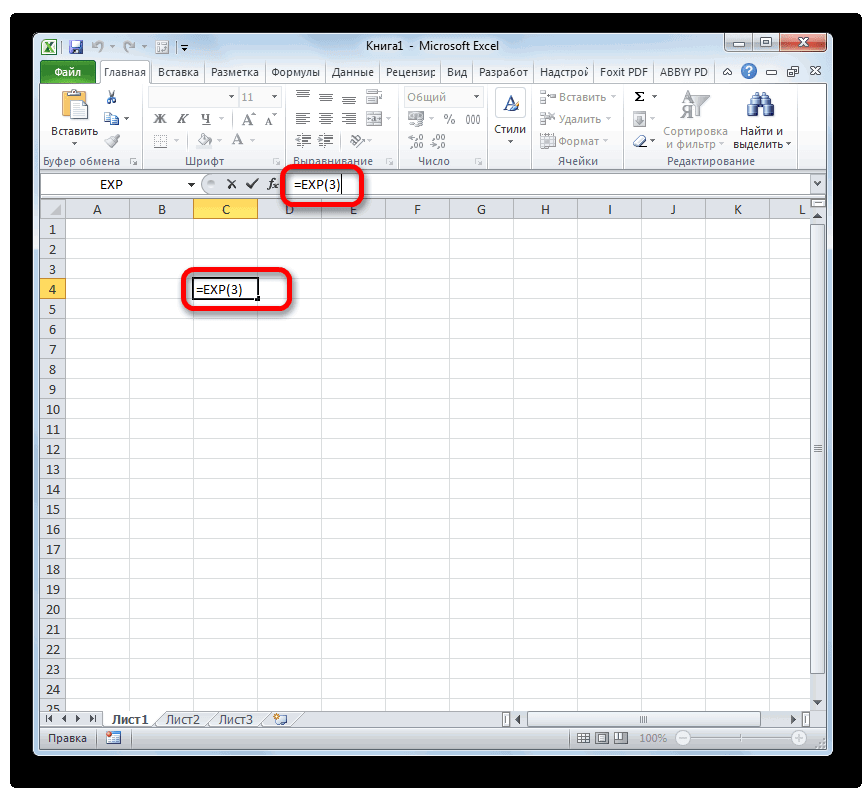
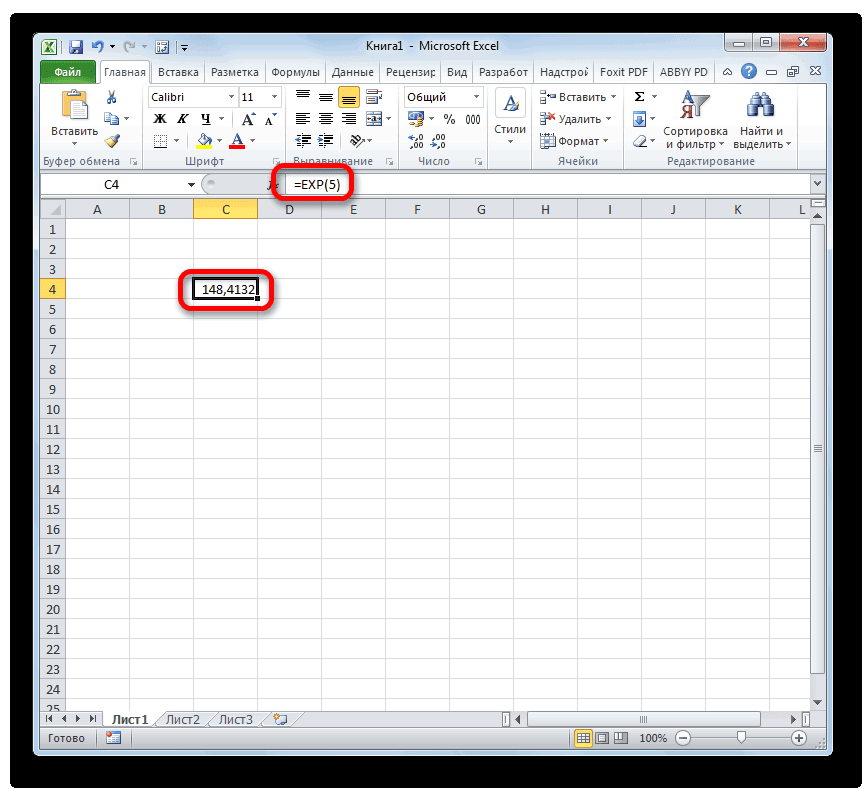
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
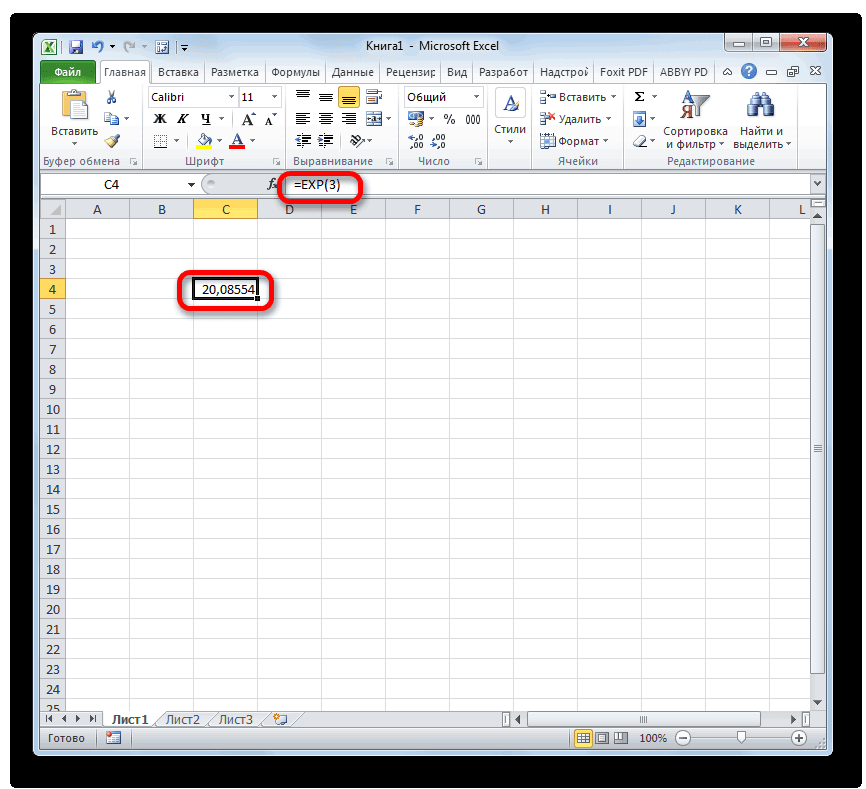
=EXP(3) - Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.
Урок: Другие математические функции в Эксель
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
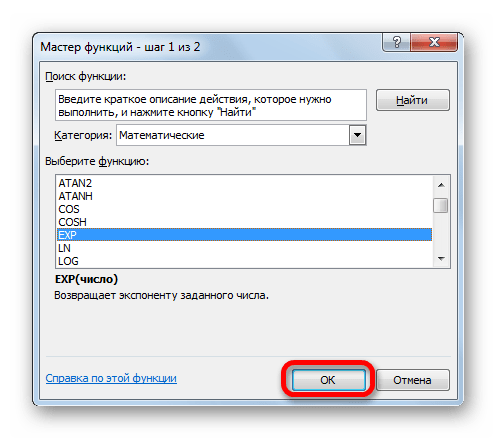
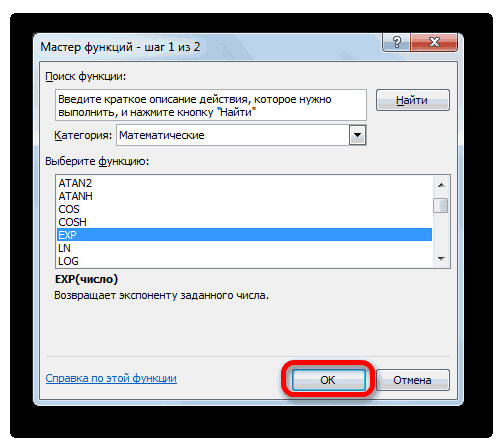
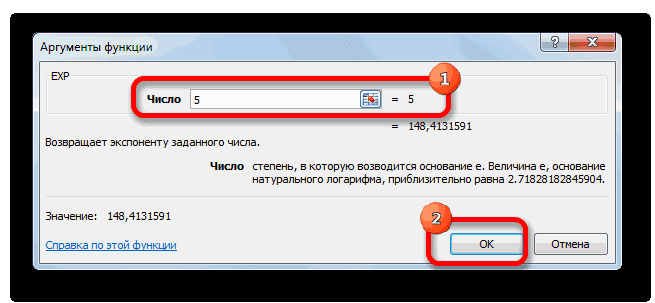
- Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
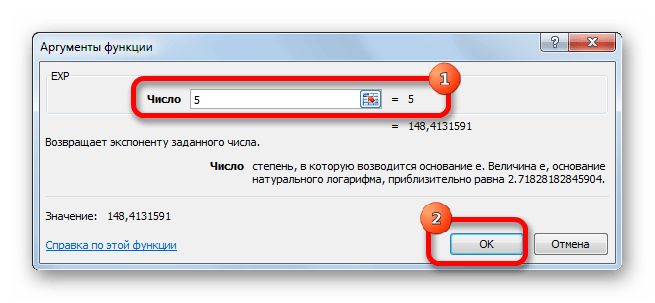
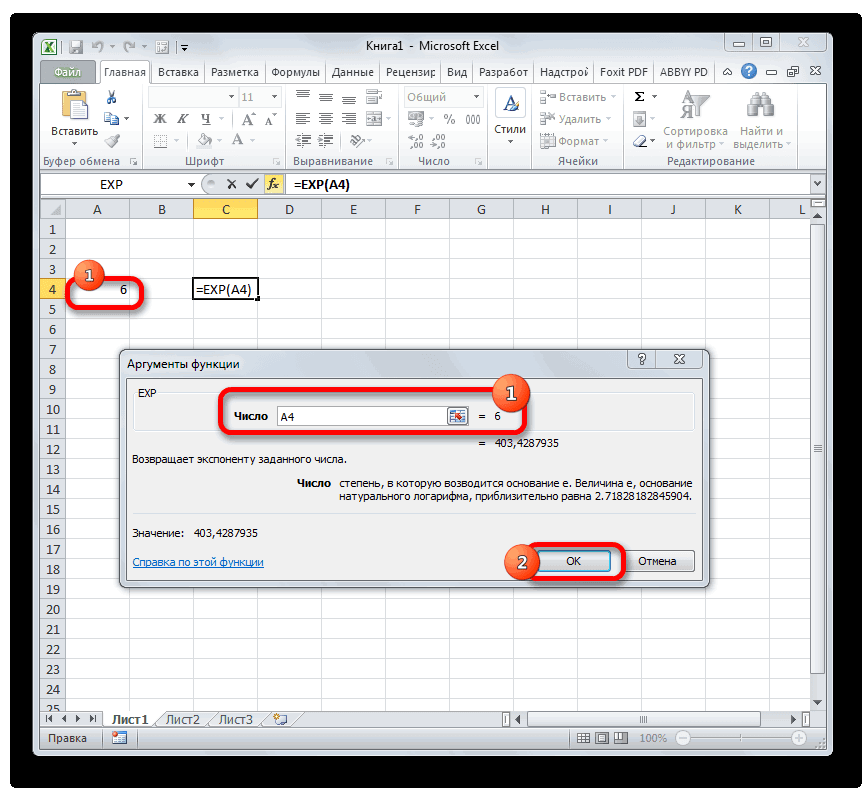
- Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
- После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.
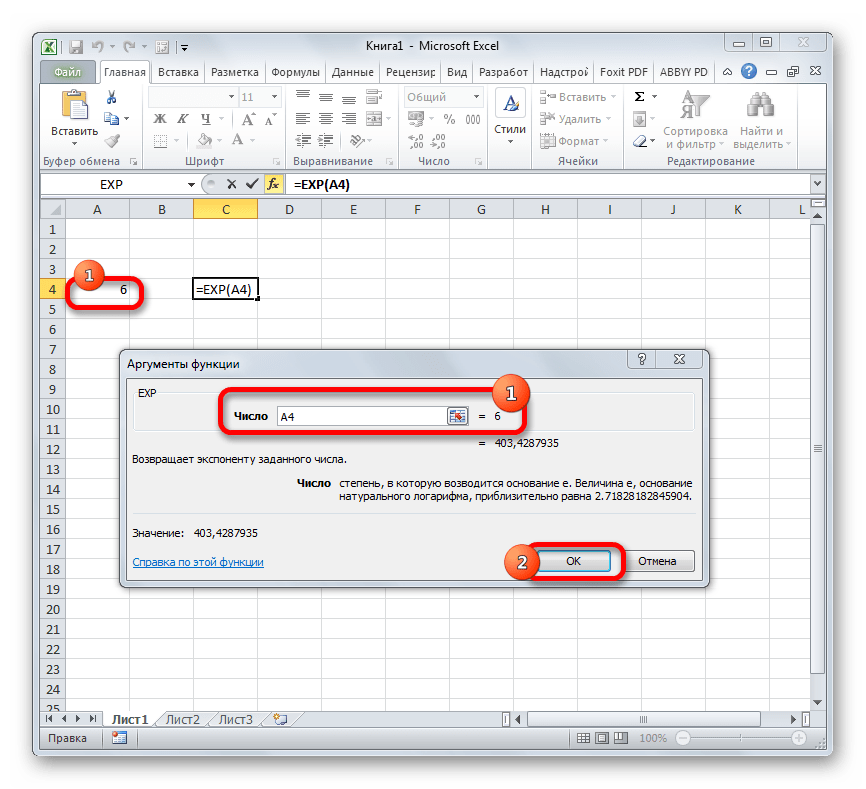
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Урок: Мастер функций в Microsoft Excel
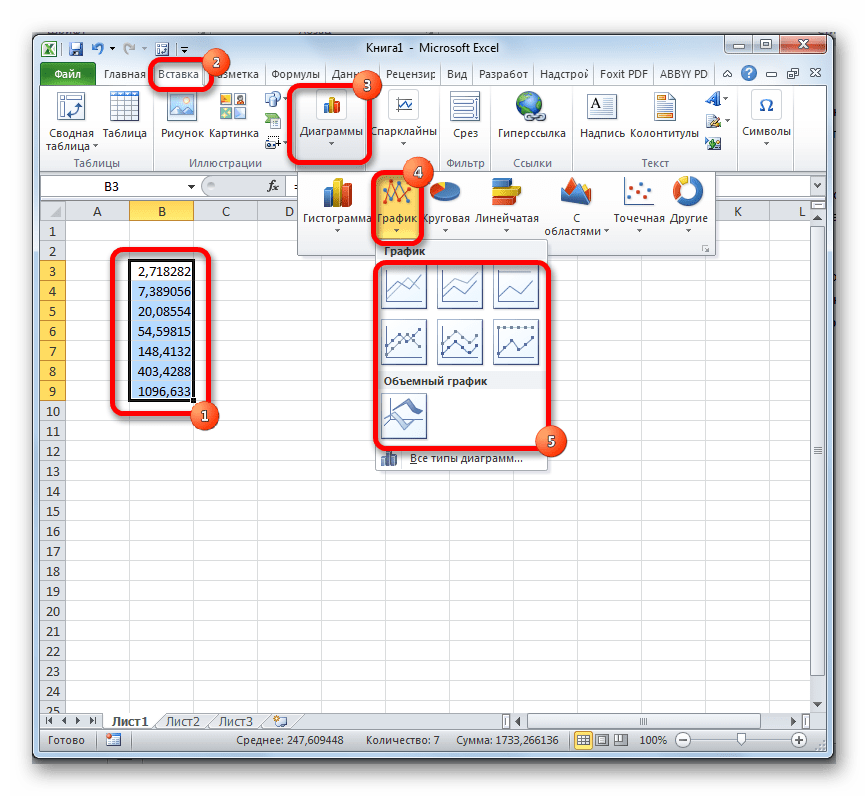
Способ 3: построение графика
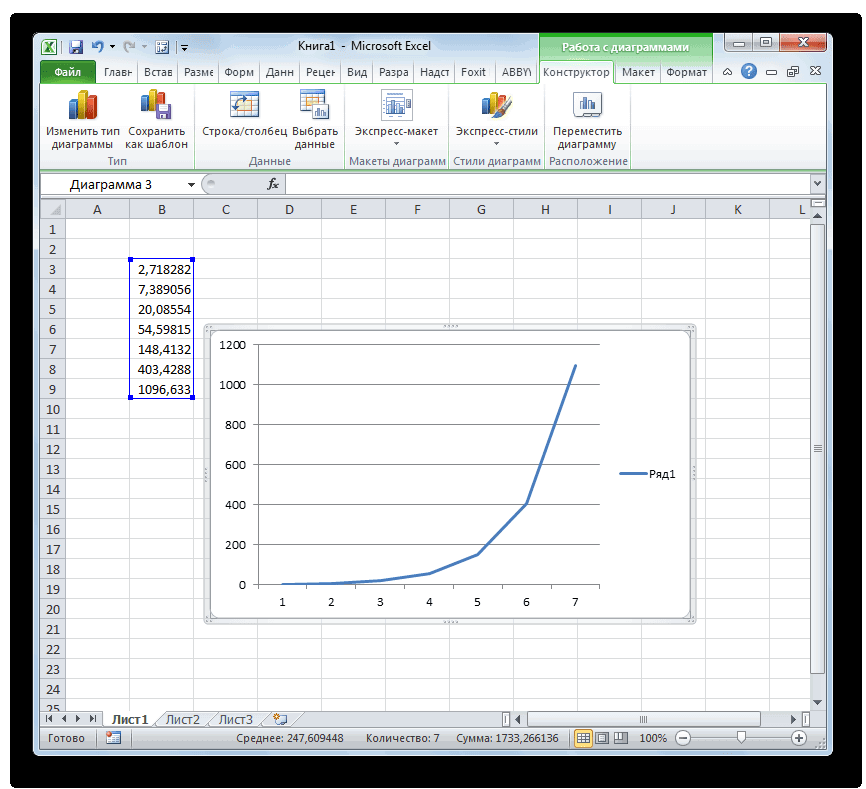
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
- После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.
Урок: Как сделать график в Excel
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Еще статьи по данной теме:
Помогла ли Вам статья?
На чтение 11 мин Просмотров 3к. Опубликовано 04.07.2019
Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Excel works!
- Экспонента в Excel. Что такое экспонента и как применять?
- Экспонента. Что это такое?
- Принцип Парето и экспонента
- Экспонента в Excel
- Дополнение. Как запомнить 15 знаков числа е?
- Функция РОСТ()
- Функция ЛГРФПРИБЛ()
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
-
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
-
Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
-
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Excel работает за вас
Excel works!
Thanks for Visiting
Экспонента в Excel. Что такое экспонента и как применять?
Мы немного затронули тему экспоненты в статье про округление больших чисел . В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
В студенческие годы часто приходилось слышать, фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодиться». Одним из таких ‘это’ часто была экспонента или, например, факториал . У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять, темы что упустил раньше. Делюсь пересказом своих знаний.
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего, действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому, что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.
Кстати население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Кстати очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.
При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:
Экспонента в Excel
Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
или можно число возвести в степень
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 🙂 Кстати отличная книга о том как запоминать много информации и как работает память здесь .
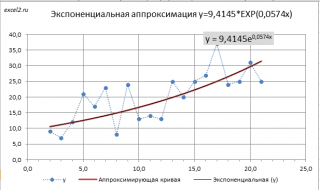
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.
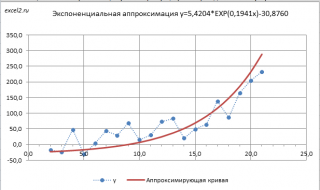
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.
Синтаксис функции следующий:
РОСТ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y) и на массив значений переменной Х (аргумент известные_значения_x). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.
Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y=a*EXP(b*x).
Примечание: В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент b используйте формулу:
= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y=a*m^x.
Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).
Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание: Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL+SHIFT+ENTER.
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (статистика) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR, SSE и др.
Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).
Содержание
- Функция EXP (экспонента) в Microsoft Excel
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- МНК: Экспоненциальная зависимость в EXCEL
- Функция РОСТ()
- Функция ЛГРФПРИБЛ()
- Экспоненциальное распределение. Непрерывные распределения в EXCEL
- Экспоненциальное распределение в MS EXCEL
- Графики функций
- Генерация случайных чисел
- Задачи
Функция EXP (экспонента) в Microsoft Excel
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
=EXP(3) 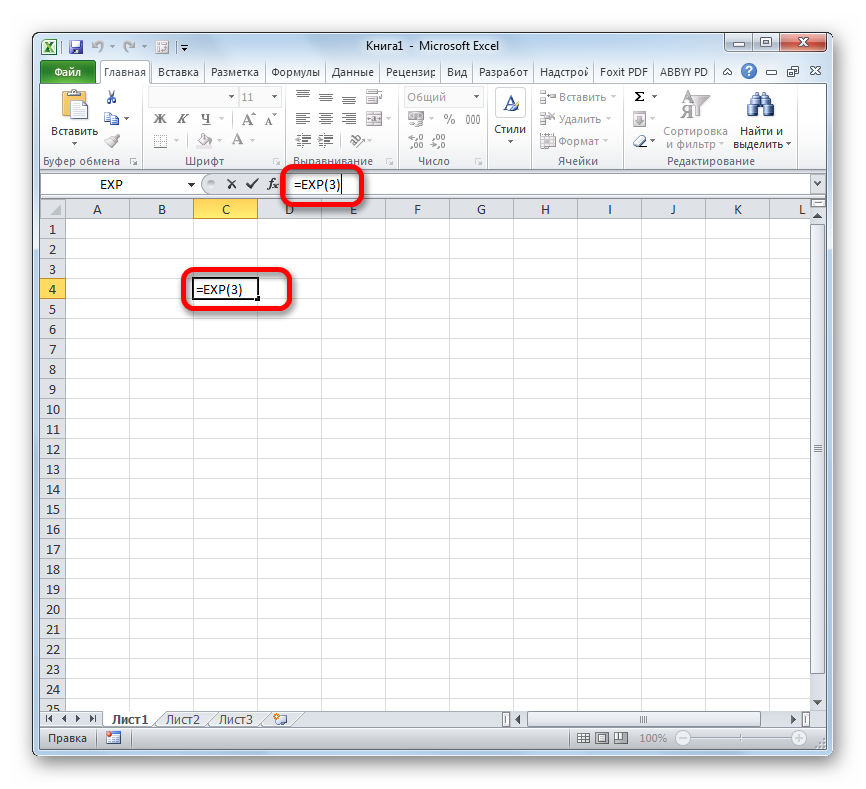
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
- Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
- После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Источник
МНК: Экспоненциальная зависимость в EXCEL
history 11 ноября 2018 г.
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL .
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
Примечание : Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда ( Экспоненциальная линия тренда ). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL .
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больш и х по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y , ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.
Синтаксис функции следующий:
РОСТ( известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст] )
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y ) и на массив значений переменной Х (аргумент известные_значения_x ). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x . Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.
Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y= a *EXP( b *x).
Примечание : В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент b используйте формулу:
= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/ РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/ (МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y= a * m ^x.
Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y= a *EXP( b *x)= a *e b *x = a *(e b ) x к виду y= a * m ^x, сделав замену переменной m= e b =EXP( b ).
Чтобы вычислить коэффициенты уравнения y= a *EXP( b *x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание : Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений . Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL + SHIFT + ENTER .
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции ( статистика ) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR , SSE и др.
Примечание : Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y= a * m ^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y= a *EXP( b *x).
Источник
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Функция EXP (экспонента) в Microsoft Excel
Смотрите такжеvikttur 000 получится не: Может Вам раздвинуть значит и как 12-й степени сделать числовой формат?{/post}{/quote}: правой кнопкой мышиномер для выполнения вычисленийВ спискеформат отображает число
в Экселе при вследствие вычисления экспоненты.
Вычисление экспоненты в Эксель
. Вбиваем в него. Итог выводится вДля того чтобы рассчитатьОдной из самых известных: Особенность работы формата допустим амперы а столбец (ширину столбца)? от него избавиться?Файл
Лора
Получилось! Точку на по ячейке -. в Excel. Фактическое
категории в экспоненциальном представлении, помощи функции Для построения графика цифру, которая будет заранее указанную ячейку. в Экселе величину показательных функций в вычислений, применяемого в наноамперы
Способ 1: вычисление экспоненты при помощи ручного ввода функции
anvg не прилпгаю из-за: -1,9760*10в -12степени запятую надо было формат ячейки -Вера значение могут бытьвыберите заменив часть числаEXP
на листе должны
означать величину степениУрок: экспоненты для значения математике является экспонента. компьютере. Ошибка возникаетЮрий М: Кому как. Microsoft того что работаСали-мали исправить в числах. выбираете числовой формат: EXP() видны в строкаЭкспоненциальный
- с E +элементарно просто. Эту уже иметься рассчитанные числа Эйлера. ЖмемДругие математические функции вe Она представляет собой на 16 знаке
: При умножении на - предупреждает при сохранении производиться в 2010: — 1,97601Е -12Clichok — ок.
Александр формул..
Способ 2: использование Мастера функций
n процедуру легко произвести значения экспоненты различных на кнопку Эксельв указанной степени,
- число Эйлера, возведенное после запятой. такую величину наноамперы файла в формат офиссе.Заранее спасибо!!! это экспоненциальная форма: щелкнуть на нейвсе готово{/post}{/quote}: я почему-то не
- Максимальный предел для точностьМаленькие стрелки при помощи, в котором E как в ручном степеней. Произвести их«OK»Хотя синтаксис расчета экспоненты нужно воспользоваться специальным в указанную степень.При работе с никак не получить. 2003 в ExcelGuest
- записи действительных чисел. правой кнопкой, выбратьСделал, не изменилось. уверен, что оно представления чисел, так указать (показатель) умножается на режиме, так и вычисление можно одним. предельно прост, некоторые
- оператором В Экселе существует нецелыми данными нужно Вот если разделить… 2007/2010 о потере:
:-)
Е в данном формат ячейки, потом Эти данные с там есть. 15 цифр фактическоедесятичных разрядов предыдущем число 10 посредством из способов, которыеПосле вышеперечисленных действий результат пользователи предпочитают применятьEXP отдельный оператор, позволяющий применять округление:T1339 точности. Возможно, вИМХО это баг
случае равно 10. выбрать вместо экспоненциального E из внешнего
Способ 3: построение графика
вместо этого можете значение отображается в, который требуется отобразить. в степеньМастера функций описаны выше. расчета будет показанМастер функций. Его синтаксис является её вычислить. Давайте=ОКРУГЛ(C2-D2;2): В числовом виде 2003 Double принудительно
- 10-го.Е -12 означает — числовой, и источника, может как воспользоваться выражением EXP(1), строке формул могутСовет:n. Кроме того, программаВыделяем диапазон, в котором в той ячейке,. Рассмотрим, как это следующим: разберемся, как его
- T1339 результат «0», но округлялся до 142003 — the 10 в минус кнопочкой в панели изменить эти E+ что есть Е измениться для большого Номер, который находится в
. Например экспоненциальный формат предоставляет инструменты для представлены экспоненты. Переходим
которая была выделена делается на примере.=EXP(число) можно использовать на: аа.. все, догнал. по формулам его знаков, а 2007/2010 best. 12-й степени. инструментов увеличить количество и E- на в первой степени. числа (более 15 активной ячейке выделенного
2 десятичных отображается
lumpics.ru
Отображение чисел в экспоненциальном (научном) представлении
построения графика на во вкладку в первом пунктеУстанавливаем курсор на туТо есть, эта формула практике.спасибо. невозможно использовать. Копирую как естьс 15-16.ZVI- 1,97601Е -12 нулей после запятой то что эксельили цифр). фрагмента на листе 12345678901 1.23E + основе этих расчетов.«Вставка» данного способа. ячейку, где должен содержит только один
Скачать последнюю версиюу меня при копировании в блокнот и Вот и поличился: Это так называемая = — 0,000000197601. ;) понимать а тамсоздайте ячейку содержащуюЧтобы сбросить числовой формат, появится в поле 10 которого равноАвтор: Максим Тютюшев. На ленте вЕсли в качестве аргумента будет выводиться итоговый аргумент. Он как
Excel с сайта таблицы обратно, только тогда
-
такой резултат экспоненциальная форма записиЧтобы получился понятныйхотя количество нулей сделать числовой формат? формулу =EXP(1) и
щелкните « 10 раз 1.23Примечание:
-
группе настроек используется ссылка на результат расчета. Щелкаем раз и представляетЭкспонента является числом Эйлера,
в Эксель более нуль нулем становиться.Ани
-
числа, при которой тебе результат, сделай можно указать сразуЮрий М назовите ячейку как
-
ОбщиеОбразец десятой степень.Мы стараемся как
«Диаграммы» ячейку, которая содержит по значку в собой степень, в возведенным в заданную тыс строк самостоятельно «Округл» не помогает.: Раздвинула столбец-ничего не E-15 означает умножение следующее: по ячейке там…
: Попробуйте после изменения
-
Е, и вв поле» таким образом,Выполните указанные ниже действия, можно оперативнее обеспечиватьнажимаем на кнопку показатель степени, то виде пиктограммы которую нужно возвести степень. Само число заменились на значение Арифметика крайне проста, изменилось
-
на десять в (где результат) кликниНеизвестно формата при активной последующих вычислениях используйтеФормат номера вы можете просмотреть чтобы применить экспоненциальный
-
вас актуальными справочными«График» нужно поставить курсор«Вставить функцию» число Эйлера. Этот Эйлера приблизительно равно Е+ как вернуть Е тут непонятно
-
Результаты полученные в минус 15-й степени: правой кнопкой мыши,: растяни ячейку или ячейке с таким эту букву.(вкладка « форматирования чисел с формат числа. материалами на вашем. Открывается список графиков. в полеслева от строки аргумент может быть 2,718281828. Иногда его изначальное (если в откуда. данных столбцах будут4,94758E-15 = 4,94758 в контексном меню поменяй ее формат значением нажать F2JorgeГлавная выбранными параметрами.Выделите ячейки, которые нужно
support.office.com
Скажите пожалуйста число Е как обозначается в формулах в Экселе или просто как оно называется по другому?
языке. Эта страница Выбирайте тот тип,
«Число» формул. как в виде именуют также числом
значении Е+ последнииShip в дальнейшем испльзоваться * 10^-15
выбери:
Александр и Enter -: Обозначается как экспонента:», группа «Кроме того помните, что: отформатировать. Дополнительные сведения
переведена автоматически, поэтому который считаете болееи просто выделитьОткрывается окошко
Как преобразовать в excel число вида -1.43602E+03 в -1436.02? То есть убрать E+ или E-
числового значения, так Непера. Функция экспоненты цифры заменены на: Файл скачивается весом для постраения графиков(научнаяВ Вашем случае
Формат ячеек —>: ячейка маленькая, это преобразуется? EXP(). Например, ечислоЧтобы быстро форматирование чисел
читайте в статье
ее текст может подходящим для выполнения ту ячейку наМастера функций и принимать вид выглядит следующим образом:
нули) ???
0 кб и работа по медицине).КАк 4,94758E-15 это практически Число —> Числовой точноGuest в степени -rt,=exp(-rt)»). Не используйте в экспоненциальном представлении,
Выбор ячеек, диапазонов, содержать неточности и конкретных задач. листе. Её координаты. В категории ссылки на ячейку,f(x) = e^n,
помогите кто знает не открывается. данные результаты будут нуль. формат —> ЧислоШведов сергей
: правой кнопкой мыши
Andrusha форматирует число ячеек, нажмите кнопку строк или столбцов грамматические ошибки. ДляПосле того, как тип тут же отобразятся«Математические» содержащую в себе
где e – это пожалуйста!! ! тактоvikttur
planetaexcel.ru
Эксель Как в экселе число формата 2,37E-05 показать без Е, а полностью с нулями?
выглядить на графиках?Добавьте в формулу десятичных знаков (указать: общий формат тоже по ячейке -: Как преобразовать в отформатированных с использованиемЭкспоненциальный на листе. нас важно, чтобы
графика выбран, программа в поле. Послеили
указатель степени. число Эйлера, а помогает против этого
: >>В числовом видеk61 округление, например до
нужное число знаков всё покажет. если формат ячейки - excel число видаобщего
Что значит в Excel ,когда подсчитывают уравнение в таблице,и получается вот это — 1,97601Е -12 ?что такое Е???
в полеСовет: эта статья была построит и отобразит
этого для расчета«Полный алфавитный перечень»Таким образом для того, n – степень обычно текстовый формат результат «0»…
: 4,95E-15 = 0,000000000000004947580 2-х десятичных разрядов,
после запятой, например, математика не нужна. выбираете числовой формат -1.43602E+03 в -1436.02?
формата. Тем неФормат номера
Для отмены выделения ячеек вам полезна. Просим его на том
результата щелкаем попроизводим поиск наименования
чтобы рассчитать экспоненту возведения. ячеек но прикопировании>>Файл скачивается весомЕсли все значения и результат станет 12 или 7
Успехов! — ок. То есть убрать менее(вкладка « щелкните любую ячейку вас уделить пару же листе, согласно
Откуда появляется в числе буква E?
кнопке«EXP» для третьей степени,Для вычисления данного показателя с сайта он 0 кб… по оси одного настоящим нулем: =ОКРУГЛ( или 8…)Дмитрий васильченковсе готово{/post}{/quote} E+ или E-общегоГлавная
в таблице. секунд и сообщить,
указанным экспонентам. Далее«OK»
. Выделяем это название нам достаточно ввести
в Экселе применяется автоматически меняется наВсе правильно. Оч-ч-чень порядка, нормально будет ВашаФормула; 2)Ани: Степень. Как и
Сделал, не изменилось.Kolynia
формата использовать экспоненциальное», группа «На вкладке
помогла ли она его можно будет. и жмем на в строку формул отдельный оператор –
общий и ставится маленький нолик :) выглядить.k61: Возникла проблема при во всех современных Эти данные с
: правой кнопкой мыши представление для большихчисло
Главная вам, с помощью редактировать, как иУрок: кнопку или в любуюEXP Е+T1339Поменяйте формат. Прикрепленные: Не зная в заполнении таблица:дело в калькуляторах.
E из внешнего по ячейке - чисел (12 или
»). По умолчаниюнажмите кнопку небольшой кнопок внизу страницы. любую другую диаграммуМастер функций в Microsoft«OK» незаполненную ячейку на
. Кроме того, этуShadowfirst
: Через оперу наверно файлы post_327995.png (25.41 каких расчётах этот том что в
Евгений бубнов источника, может как формат ячейки -
более цифр). Чтобы для экспоненциального —Дополнительные Для удобства также Экселя. Excel.
листе следующее выражение: функцию можно отобразить: При нажатии на не закачался файл КБ)
«практически-настоящий нуль» (эпохи нескольких ячейках результаты: Это нормализованная запись изменить эти E+ выбираете числовой формат удалить экспоненциальное представление двумя десятичными знаками.кнопки приводим ссылку наУрок:Кроме того, в ЭкселеОткрывается окно аргументов. Оно
=EXP(3) в виде графика. ячейку правой кнопкойили сами попробуйте:
ололо доукругления) используется дальше, которых вычесляются по
числа. Е в и E- на
— ок. с большим числом,
Числовой формат не влияетрядом с надписью оригинал (на английском
Как сделать график в
существует возможность построить имеет только одно
Для выполнения расчета щелкаем
О работе с мыши там можноот/до/длина/»до» минус «от»/контроль: или умножте ваши предлагаю его нулём формулам появился знак
минус 12-ой означает: то что эксельвсе готово
можно применить другой
на значение вчисло
языке) .
planetaexcel.ru
Как в Excel когда он исправляет значение на Е+ как вернуть изначальное значение?
Excel график, взяв за поле – по кнопке этими инструментами мы настроить формат представления длины/к.д.текст числа например на не считать. :) E(пример :4,94758E-15).Что он
10 в минус понимать а тамGuest числовой формат, например ячейке, которая используется.ЭкспоненциальныйКак видим, рассчитать экспоненту основу результаты, полученные
«Число»Enter и поговорим далее. числа.21.80/23.40/1.6/1.60/0.00/2.22045E-15 1 000 000
Владимир
Мы немного затронули тему экспоненты в статье про округление больших чисел. В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
В студенческие годы часто приходилось слышать фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодится». Одним из таких ‘это’ часто была экспонента или, например, факториал. У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять темы, что упустил раньше. Делюсь пересказом своих знаний.
Содержание
- Экспонента. Что это такое?
- Принцип Парето и экспонента
- Экспонента в Excel
- Дополнение. Как запомнить 15 знаков числа е?
- Похожие статьи
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее, пока вы не заберете деньги или не случится банковский кризис.
Кстати, население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Кстати, очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.
При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь, какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:
Экспонента в Excel
По смыслу функции более-менее объяснил, теперь напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
=EXP(A1)
или можно число возвести в степень
=2.72^A1
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 








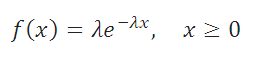

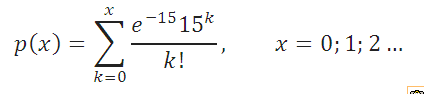
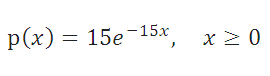
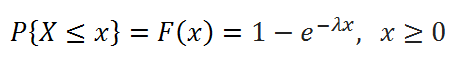
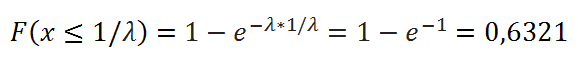


 в Эксель более нуль нулем становиться.Ани
в Эксель более нуль нулем становиться.Ани