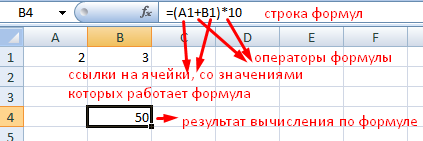
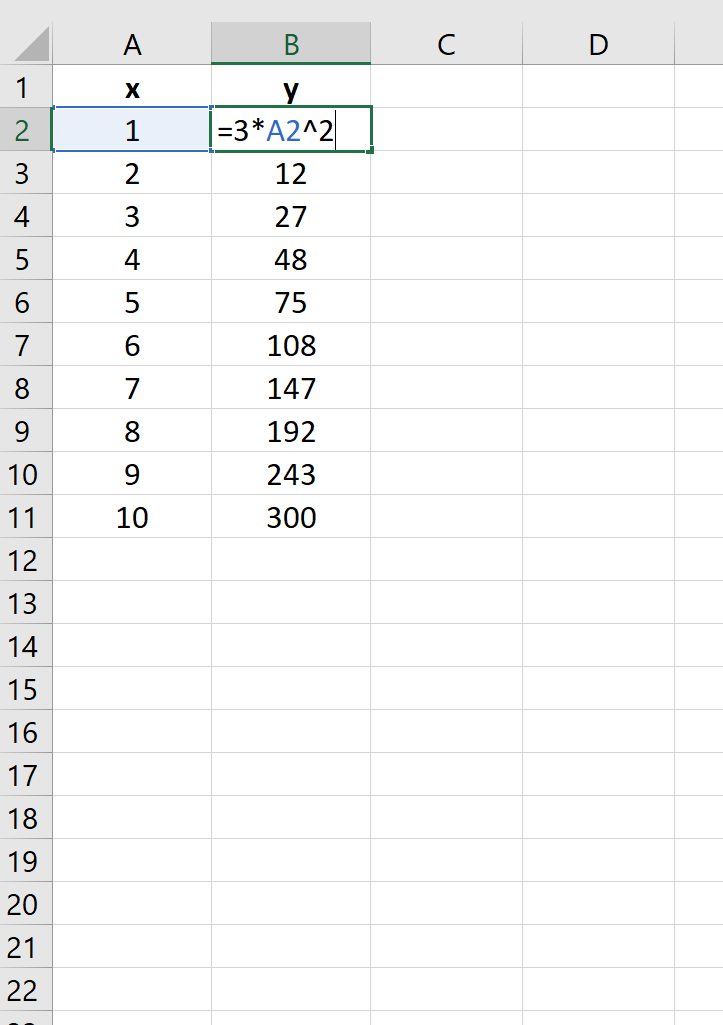
Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе.
Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.
Формулы в Excel для чайников
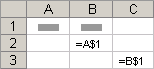
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.
В Excel применяются стандартные математические операторы:
| Оператор | Операция | Пример |
| + (плюс) | Сложение | =В4+7 |
| — (минус) | Вычитание | =А9-100 |
| * (звездочка) | Умножение | =А3*2 |
| / (наклонная черта) | Деление | =А7/А8 |
| ^ (циркумфлекс) | Степень | =6^2 |
| = (знак равенства) | Равно | |
| < | Меньше | |
| > | Больше | |
| <= | Меньше или равно | |
| >= | Больше или равно | |
| <> | Не равно |
Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
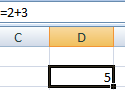
Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.
Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.
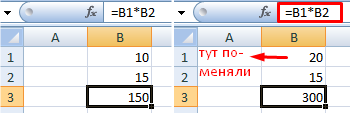
При изменении значений в ячейках формула автоматически пересчитывает результат.
Ссылки можно комбинировать в рамках одной формулы с простыми числами.
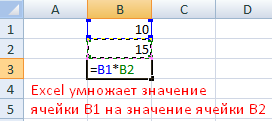
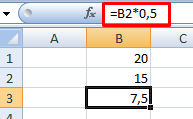
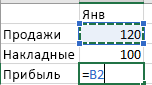
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.
В нашем примере:
- Поставили курсор в ячейку В3 и ввели =.
- Щелкнули по ячейке В2 – Excel «обозначил» ее (имя ячейки появилось в формуле, вокруг ячейки образовался «мелькающий» прямоугольник).
- Ввели знак *, значение 0,5 с клавиатуры и нажали ВВОД.
Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:
- %, ^;
- *, /;
- +, -.
Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.
Как в формуле Excel обозначить постоянную ячейку
Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.
Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.
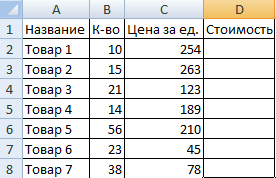
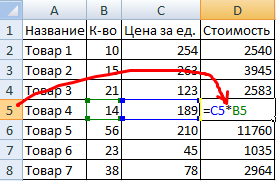
- Вручную заполним первые графы учебной таблицы. У нас – такой вариант:
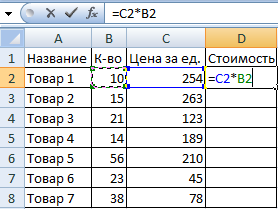
- Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
- Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
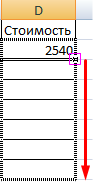
Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.
Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.
Ссылки в ячейке соотнесены со строкой.
Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).
Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.
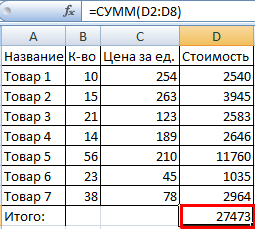
- Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9
- Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
- После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.
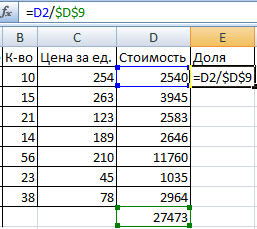
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:
- Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.
- Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
- Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.
При создании формул используются следующие форматы абсолютных ссылок:
- $В$2 – при копировании остаются постоянными столбец и строка;
- B$2 – при копировании неизменна строка;
- $B2 – столбец не изменяется.
Как составить таблицу в Excel с формулами
Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.
Простейшие формулы заполнения таблиц в Excel:
- Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+»=», чтобы вставить столбец.
- Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.
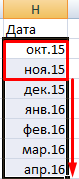
- По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
- Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» — выбираем формулу для автоматического расчета среднего значения.
Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.
Полные сведения о формулах в Excel
Начните создавать формулы и использовать встроенные функции, чтобы выполнять расчеты и решать задачи.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Важно: В этой статье мы обсудим похожие проблемы с просмотром и просмотром. Попробуйте использовать новую функцию ПРОСМОТРX , улучшенную версию функции ВЛОП, которая работает в любом направлении и по умолчанию возвращает точные совпадения, что упрощает и удобнее в использовании, чем предшественницу.
Создание формулы, ссылающейся на значения в других ячейках
-
Выделите ячейку.
-
Введите знак равенства «=».
Примечание: Формулы в Excel начинаются со знака равенства.
-
Выберите ячейку или введите ее адрес в выделенной.
-
Введите оператор. Например, для вычитания введите знак «минус».
-
Выберите следующую ячейку или введите ее адрес в выделенной.
-
Нажмите клавишу ВВОД. В ячейке с формулой отобразится результат вычисления.
Просмотр формулы
-
При вводе в ячейку формула также отображается в строке формул.
-
Чтобы просмотреть формулу, выделите ячейку, и она отобразится в строке формул.
Ввод формулы, содержащей встроенную функцию
-
Выделите пустую ячейку.
-
Введите знак равенства «=», а затем — функцию. Например, чтобы получить общий объем продаж, нужно ввести «=СУММ».
-
Введите открывающую круглую скобку «(«.
-
Выделите диапазон ячеек, а затем введите закрывающую круглую скобку «)».
-
Нажмите клавишу ВВОД, чтобы получить результат.
Скачивание книги «Учебник по формулам»
Мы подготовили для вас книгу Начало работы с формулами, которая доступна для скачивания. Если вы впервые пользуетесь Excel или даже имеете некоторый опыт работы с этой программой, данный учебник поможет вам ознакомиться с самыми распространенными формулами. Благодаря наглядным примерам вы сможете вычислять сумму, количество, среднее значение и подставлять данные не хуже профессионалов.
Подробные сведения о формулах
Чтобы узнать больше об определенных элементах формулы, просмотрите соответствующие разделы ниже.
Формула также может содержать один или несколько таких элементов, как функции, ссылки, операторы и константы.
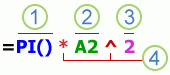
Части формулы
1. Функции. Функция ПИ() возвращает значение числа пи: 3,142…
2. Ссылки. A2 возвращает значение ячейки A2.
3. Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
4. Операторы. Оператор ^ (крышка) применяется для возведения числа в степень, а * (звездочка) — для умножения.
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, а не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после редактирования формулы. Обычно лучше помещать такие константы в отдельные ячейки, где их можно будет легко изменить при необходимости, а в формулах использовать ссылки на эти ячейки.
Ссылка указывает на ячейку или диапазон ячеек листа и сообщает Microsoft Excel, где находятся необходимые формуле значения или данные. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
-
Стиль ссылок A1
По умолчанию Excel использует стиль ссылок A1, в котором столбцы обозначаются буквами (от A до XFD, не более 16 384 столбцов), а строки — номерами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Ячейка или диапазон
Использование
Ячейка на пересечении столбца A и строки 10
A10
Диапазон ячеек: столбец А, строки 10-20.
A10:A20
Диапазон ячеек: строка 15, столбцы B-E
B15:E15
Все ячейки в строке 5
5:5
Все ячейки в строках с 5 по 10
5:10
Все ячейки в столбце H
H:H
Все ячейки в столбцах с H по J
H:J
Диапазон ячеек: столбцы А-E, строки 10-20
A10:E20
-
Создание ссылки на ячейку или диапазон ячеек с другого листа в той же книге
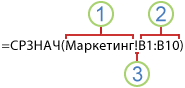
В приведенном ниже примере функция СРЗНАЧ вычисляет среднее значение в диапазоне B1:B10 на листе «Маркетинг» в той же книге.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек от B1 до B10
3. Восклицательный знак (!) отделяет ссылку на лист от ссылки на диапазон ячеек.
Примечание: Если название упоминаемого листа содержит пробелы или цифры, его нужно заключить в апострофы (‘), например так: ‘123’!A1 или
=’Прибыль за январь’!A1. -
Различия между абсолютными, относительными и смешанными ссылками
-
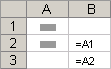
Относительные ссылки . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
Скопированная формула с относительной ссылкой
-
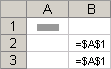
Абсолютные ссылки . Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Скопированная формула с абсолютной ссылкой
-
Смешанные ссылки . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет. При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.
Скопированная формула со смешанной ссылкой
-
-
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. В Microsoft Excel используются все листы, указанные между начальным и конечным именами в ссылке. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
-
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Что происходит при перемещении, копировании, вставке или удалении листов . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование . Если вставить листы между листами 2 и 6, Microsoft Excel прибавит к сумме содержимое ячеек с A2 по A5 на новых листах.
-
Удаление . Если удалить листы между листами 2 и 6, Microsoft Excel не будет использовать их значения в вычислениях.
-
Перемещение . Если листы, находящиеся между листом 2 и листом 6, переместить таким образом, чтобы они оказались перед листом 2 или после листа 6, Microsoft Excel вычтет из суммы содержимое ячеек с перемещенных листов.
-
Перемещение конечного листа . Если переместить лист 2 или 6 в другое место книги, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.
-
Удаление конечного листа . Если удалить лист 2 или 6, Microsoft Excel скорректирует сумму с учетом изменения диапазона листов.
-
-
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. При использовании стиля R1C1 в Microsoft Excel положение ячейки обозначается буквой R, за которой следует номер строки, и буквой C, за которой следует номер столбца.
Ссылка
Значение
R[-2]C
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце
R[2]C[2]
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее
R2C2
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца
R[-1]
Относительная ссылка на строку, расположенную выше текущей ячейки
R
Абсолютная ссылка на текущую строку
При записи макроса в Microsoft Excel для некоторых команд используется стиль ссылок R1C1. Например, если записывается команда щелчка элемента Автосумма для вставки формулы, суммирующей диапазон ячеек, в Microsoft Excel при записи формулы будет использован стиль ссылок R1C1, а не A1.
Чтобы включить или отключить использование стиля ссылок R1C1, установите или снимите флажок Стиль ссылок R1C1 в разделе Работа с формулами категории Формулы в диалоговом окне Параметры. Чтобы открыть это окно, перейдите на вкладку Файл.
К началу страницы
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Переключение между относительными, абсолютными и смешанными ссылками для функций
Использование операторов в формулах Excel
Порядок выполнения действий в формулах Excel
Использование функций и вложенных функций в формулах Excel
Определение и использование имен в формулах
Использование формул массива: рекомендации и примеры
Удаление формул
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по категориям)
Нужна дополнительная помощь?
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12689 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.
Данную систему уравнений можно представить в матричной форме:


Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:
1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://zf.bsut.by/it/fbo/zb1/lab2.htm
17 авг. 2022 г.
читать 3 мин
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Пример 1: построение линейного уравнения
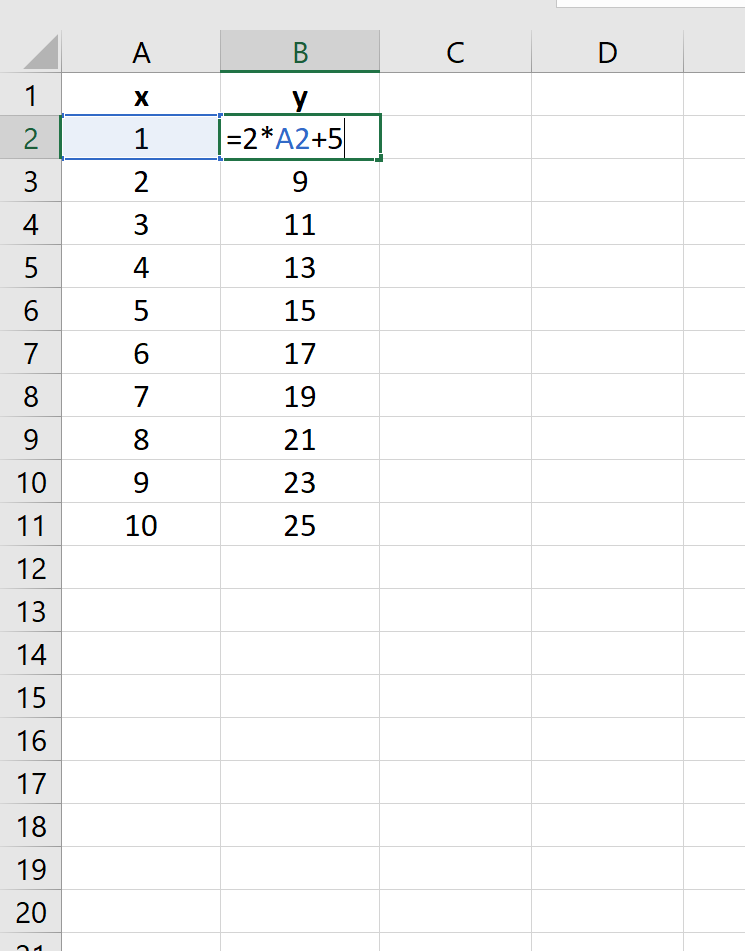
Предположим, вы хотите построить следующее уравнение:
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
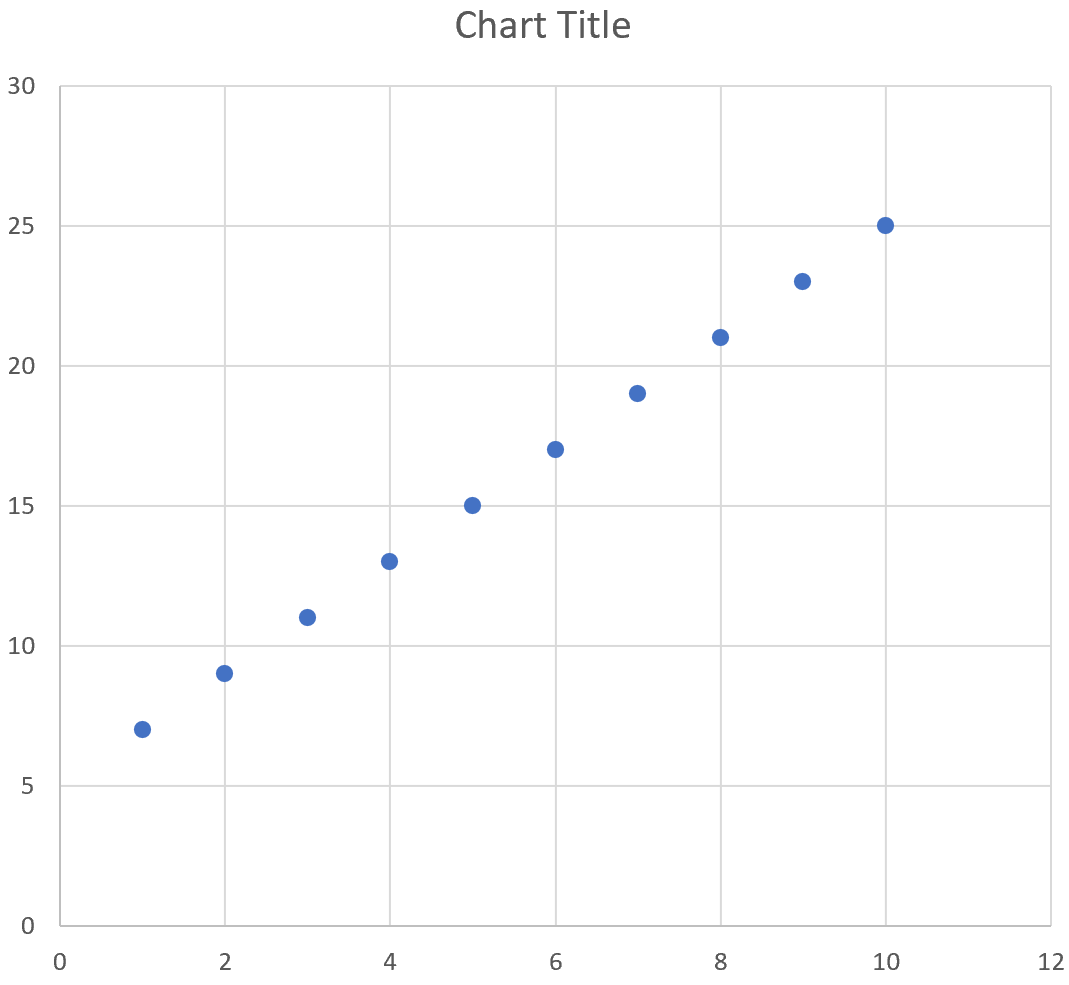
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
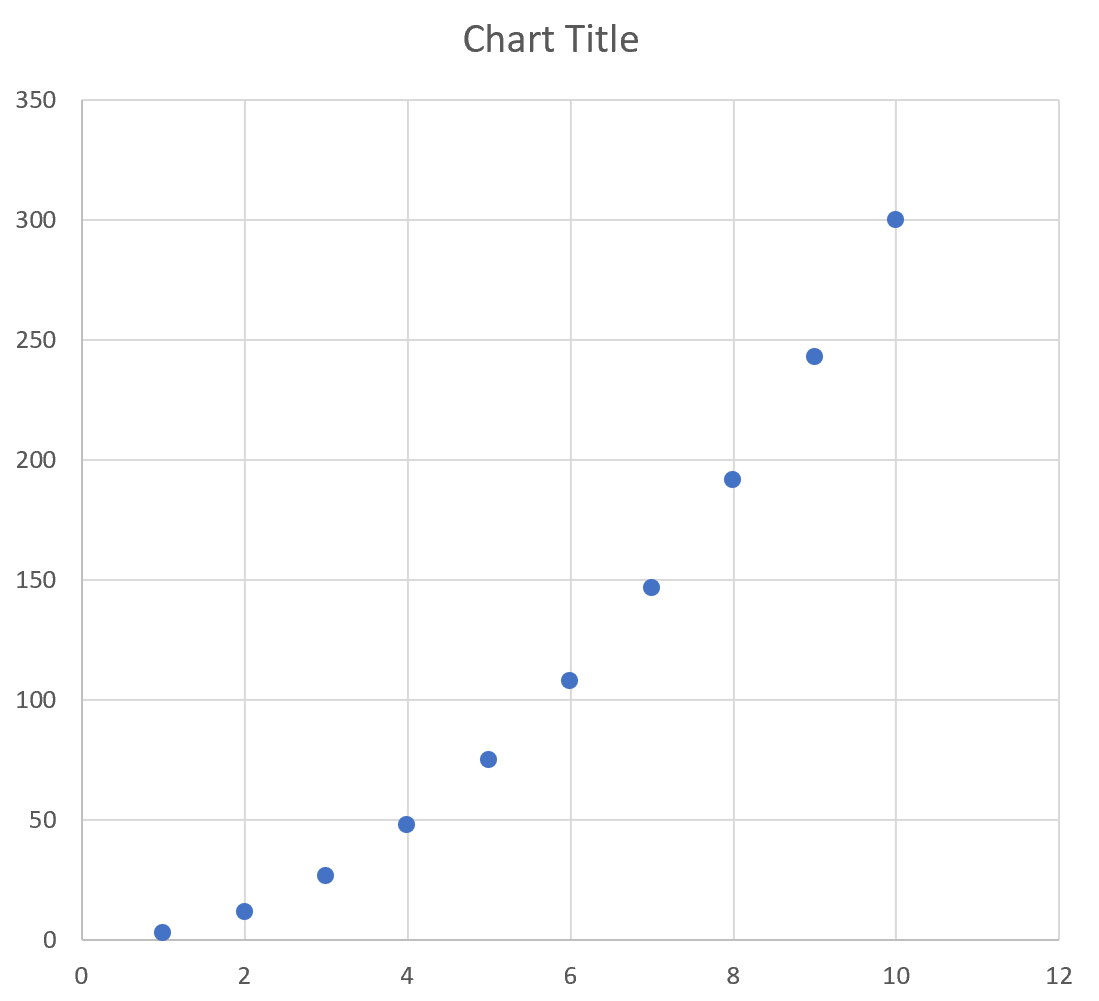
Пример 2. Построение квадратного уравнения
Предположим, вы хотите построить следующее уравнение:
у = 3x 2
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
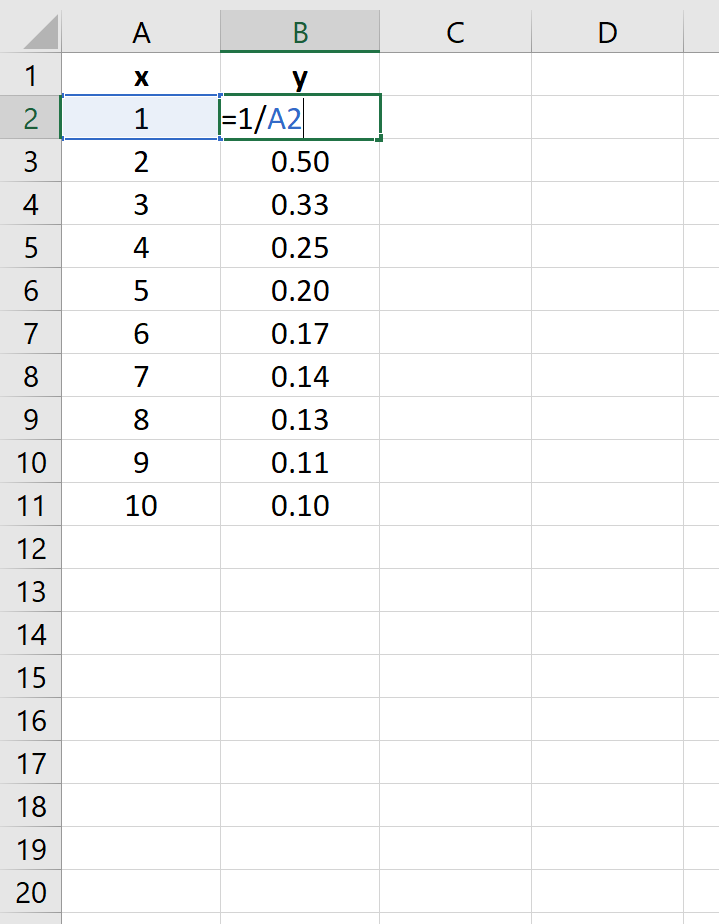
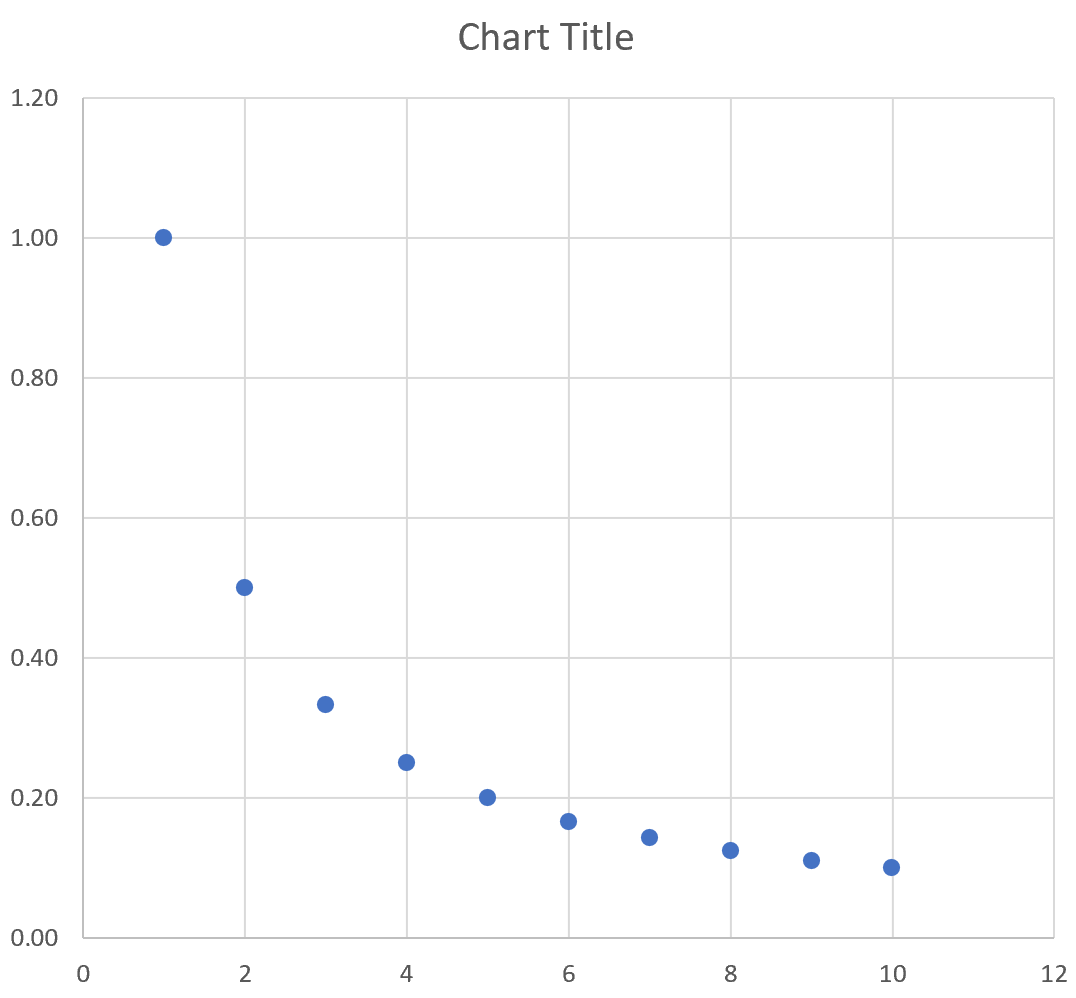
Пример 3: построение уравнения обратной связи
Предположим, вы хотите построить следующее уравнение:
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
Пример 4. Построение уравнения синуса
Предположим, вы хотите построить следующее уравнение:
у = грех (х)
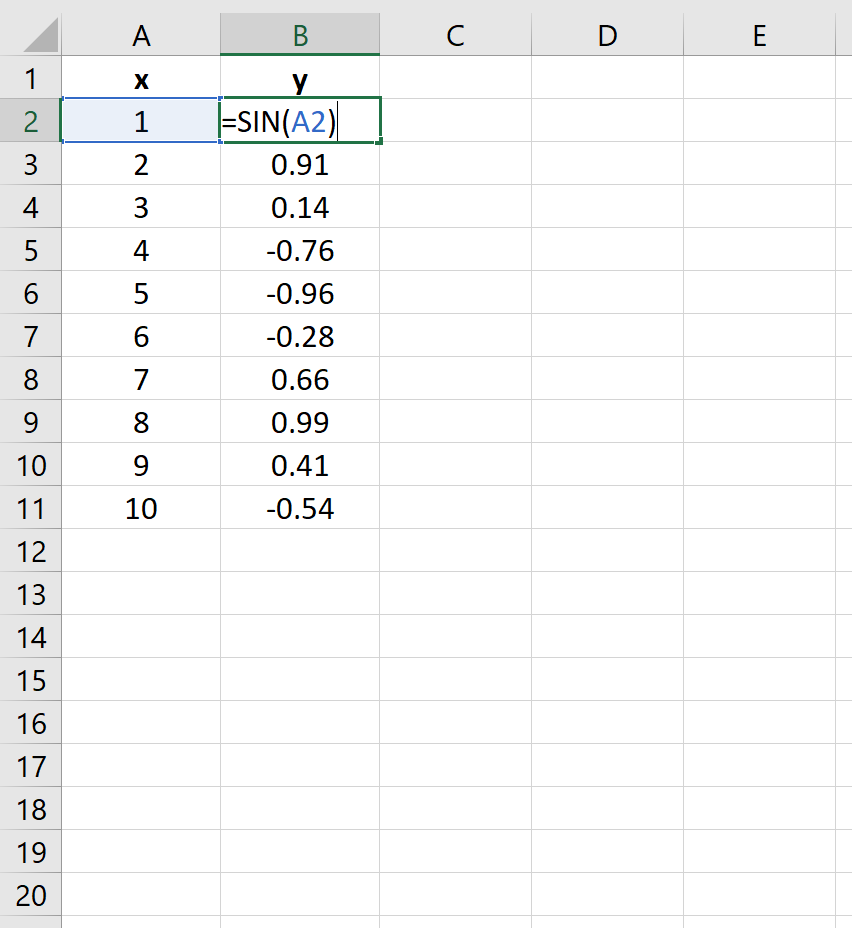
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
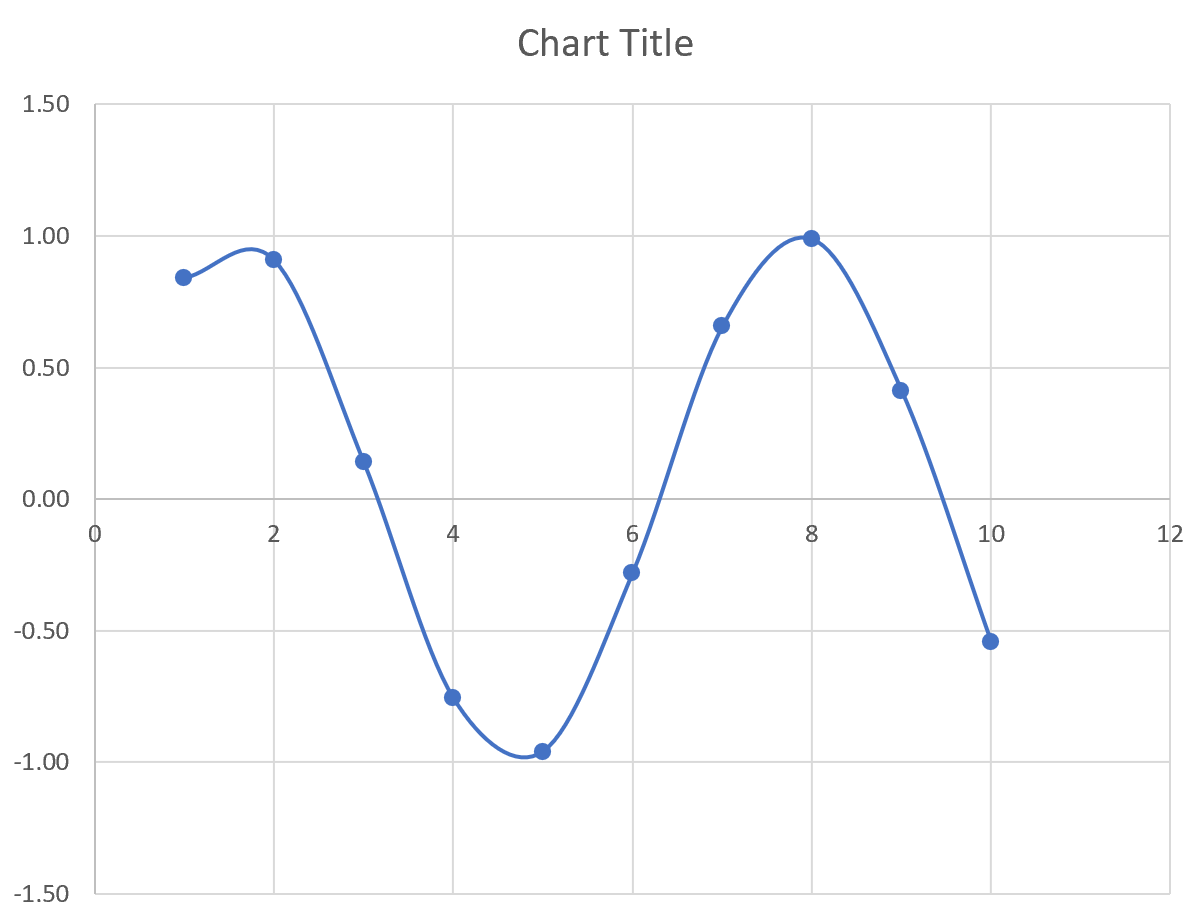
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
Вывод
Вы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.
Excel необходим в случаях, когда вам нужно упорядочить, обработать и сохранить много информации. Он поможет автоматизировать вычисления, делает их проще и надежнее. Формулы в Excel позволяют проводить сколь угодно сложные вычисления и получать результаты моментально.
Как написать формулу в Excel
Прежде чем учиться этому, следует понять несколько базовых принципов.
- Каждая начинается со знака «=».
- Участвовать в вычислениях могут значения из ячеек и функции.
- В качестве привычных нам математических знаков операций используются операторы.
- При вставке записи в ячейке по умолчанию отражается результат вычислений.
- Посмотреть конструкцию можно в строке над таблицей.
Каждая ячейка в Excel является неделимой единицей с собственным идентификатором (адрес), который обозначается буквой (номер столбца) и цифрой (номер строки). Отображается адрес в поле над таблицей.
Итак, как создать и вставить формулу в Excel? Действуйте по следующему алгоритму:
Мы узнали, как поставить и посчитать формулу в Excel, а ниже приведен перечень операторов.
Обозначение Значение
+ Сложение
— Вычитание
/ Деление
* Умножение
Если вам необходимо указать число, а не адрес ячейки – вводите его с клавиатуры. Чтобы указать отрицательный знак в формуле Excel, нажмите «-».
Как вводить и скопировать формулы в Excel
Ввод их всегда осуществляется после нажатия на «=». Но что делать, если однотипных расчетов много? В таком случае можно указать одну, а затем ее просто скопировать. Для этого следует ввести формулу, а затем «растянуть» ее в нужном направлении, чтобы размножить.
Установите указатель на копируемую ячейку и наведите указатель мыши на правый нижний угол (на квадратик). Он должен принять вид простого крестика с равными сторонами.
Нажмите левую кнопку и тяните.
Отпустите тогда, когда надо прекратить копирование. В этот момент появятся результаты вычислений.
Также можно растянуть и вправо.
Переведите указатель на соседнюю ячейку. Вы увидите такую же запись, но с другими адресами.
При копировании таким образом номера строки увеличиваются, если сдвиг происходит вниз, или увеличиваются номера столбцов – если вправо. Это называется относительная адресация.
Давайте введем в таблицу значение НДС и посчитаем цену с налогом.
Цена с НДС высчитывается как цена*(1+НДС). Введем последовательность в первую ячейку.
Попробуем скопировать запись.
Результат получился странный.
Проверим содержимое во второй ячейке.
Как видим, при копировании сместилась не только цена, но и НДС. А нам необходимо, чтобы эта ячейка оставалась фиксированной. Закрепим ее с помощью абсолютной ссылки. Для этого переведите указатель на первую ячейку и щелкните в строке формул на адрес B2.
Нажмите F4. Адрес будет разбавлен знаком «$». Это и есть признак абсолютно ячейки.
Теперь после копирования адрес B2 останется неизменным.
Если вы случайно ввели данные не в ту ячейку, просто перенесите их. Для этого наведите указатель мыши на любую границу, дождитесь, когда мышь станет похожа на крестик со стрелочками, нажмите левую кнопку и тяните. В нужном месте просто отпустите манипулятор.
Использование функций для вычислений
Excel предлагает большое количество функций, которые разбиты по категориям. Посмотреть полный перечень можно, нажав на кнопку Fx около строки формул или открыв раздел «Формулы» на панели инструментов.
Расскажем о некоторых функциях.
Как задать формулы «Если» в Excel
Эта функция позволяет задавать условие и проводить расчет в зависимости от его истинности или ложности. Например, если количество проданного товара больше 4 пачек, следует закупить еще.
Чтобы вставить результат в зависимости от условия, добавим еще один столбец в таблицу.
В первой ячейке под заголовком этого столбца установим указатель и нажмем пункт «Логические» на панели инструментов. Выберем функцию «Если».
Как и при вставке любой функции, откроется окно для заполнения аргументов.
Укажем условие. Для этого необходимо щелкнуть в первую строку и выбрать первую ячейку «Продано». Далее поставим знак «>» и укажем число 4.
Во второй строке напишем «Закупить». Эта надпись будет появляться для тех товаров, которые были распроданы. Последнюю строку можно оставить пустой, так как у нас нет действий, если условие ложно.
Нажмите ОК и скопируйте запись для всего столбца.
Чтобы в ячейке не выводилось «ЛОЖЬ» снова откроем функцию и исправим ее. Поставьте указатель на первую ячейку и нажмите Fx около строки формул. Вставьте курсор на третью строку и поставьте пробел в кавычках.
Затем ОК и снова скопируйте.
Теперь мы видим, какой товар следует закупить.
Формула текст в Excel
Эта функция позволяет применить формат к содержимому ячейки. При этом любой тип данных преобразуется в текст, а значит не может быть использован для дальнейших вычислений. Добавим столбец чтобы отформатировать итоговую сумму.
В первую ячейку введем функцию (кнопка «Текстовые» в разделе «Формулы»).
В окне аргументов укажем ссылку на ячейку итоговой суммы и установим формат «#руб.».
Нажмем ОК и скопируем.
Если попробовать использовать эту сумму в вычислениях, то получим сообщение об ошибке.
«ЗНАЧ» обозначает, что вычисления не могут быть произведены.
Примеры форматов вы можете видеть на скриншоте.
Формула даты в Excel
Excel предоставляет много возможностей по работе с датами. Одна из них, ДАТА, позволяет построить дату из трех чисел. Это удобно, если вы имеете три разных столбца – день, месяц, год.
Поставьте указатель на первую ячейку четвертого столбца и выберите функцию из списка «Дата и время».
Расставьте адреса ячеек соответствующим образом и нажмите ОК.
Скопируйте запись.
Автосумма в Excel
На случай, если необходимо сложить большое число данных, в Excel предусмотрена функция СУММ. Для примера посчитаем сумму для проданных товаров.
Поставьте указатель в ячейку F12. В ней будет осуществляться подсчет итога.
Перейдите на панель «Формулы» и нажмите «Автосумма».
Excel автоматически выделит ближайший числовой диапазон.
Вы можете выделить другой диапазон. В данном примере Excel все сделал правильно. Нажмите ОК. Обратите внимание на содержимое ячейки. Функция СУММ подставилась автоматически.
При вставке диапазона указывается адрес первой ячейки, двоеточие и адрес последней ячейки. «:» означает «Взять все ячейки между первой и последней. Если вам надо перечислить несколько ячеек, разделите их адреса точкой с запятой:
СУММ (F5;F8;F11)
Работа в Excel с формулами: пример
Мы рассказали, как сделать формулу в Excel. Это те знания, которые могут пригодиться даже в быту. Вы можете вести свой личный бюджет и контролировать расходы.
На скриншоте показаны формулы, которые вводятся для подсчета сумм доходов и расходов, а также расчет баланса на конец месяца. Добавьте листы в книгу для каждого месяца, если не хотите, чтобы все таблицы располагались на одном. Для этого просто нажмите на «+» внизу окна.
Чтобы переименовать лист, два раза на нем щелкните и введите имя.
Таблицу можно сделать еще подробнее.
Excel – очень полезная программа, а вычисления в нем дают практически неограниченные возможности.
Отличного Вам дня!