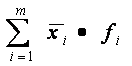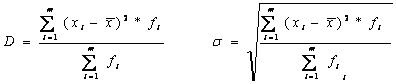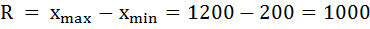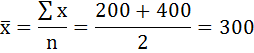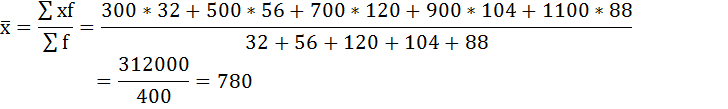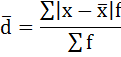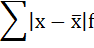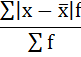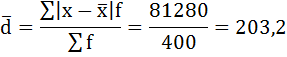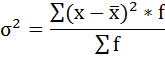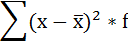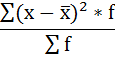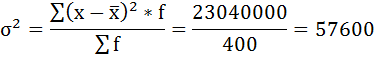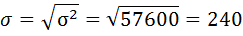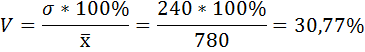Количественные данные следует определить как «Числовые».
2. Для выполнения расчета необходимо закрыть имеющиеся открытые интервалы – первый – «до 500», последний — «от 700».
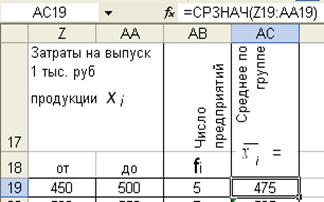
Формула вычисления левой границы первого интервала вводится в ячейку Z19 : «=АА19-(АА20-Z20)» (– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
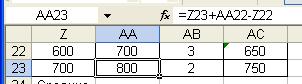
Правая граница последнего интервала в ячейку АА23 устанавливается формулой «=Z23+АА22-Z22» (от значения в ячейке Z23 откладывается размер предшествующего интервала «АА22-Z22»).
3. 
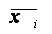
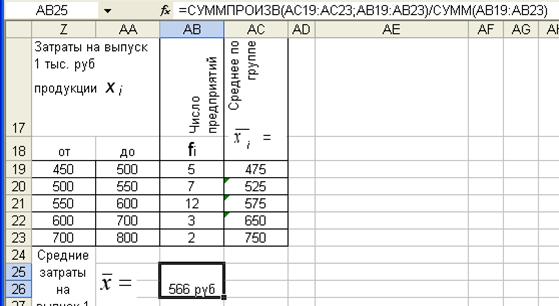
4. Рассчитывается величина средней взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель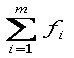
Дисперсия. Среднее квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут вычисляться по простой и взвешенной формулам.
Дисперсия, среднее квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО зарплаты подразделения:
1. Исходные значения признака хi надо записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
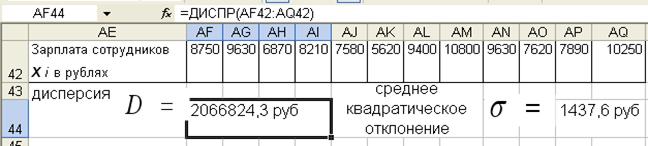
2. В ячейку результата дисперсии (например «AF44») установить функцию ДИСПР(AF42:AQ42)
1. В ячейку результата СКО (например «AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Знак «^0,5» — означает возведение в степень 0,5 величины стоящей перед ним.
Дисперсия, среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
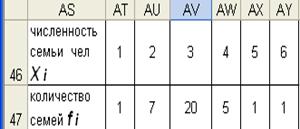
1. Исходные значения признака хi и частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
1. Рассчитать среднее арифметическое взвешенное — в примере в ячейке AW49 установлена формула =СУММПРОИЗВ (AT46:AY46;AT47:AY47)/СУММ(AT47:AY47)
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 266
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 171
- БГТУ 602
- БГУ 153
- БГУИР 391
- БелГУТ 4908
- БГЭУ 962
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 119
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 497
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 130
- ИжГТУ 143
- КемГППК 171
- КемГУ 507
- КГМТУ 269
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2909
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 107
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 367
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 330
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 636
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 454
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 212
- НУК им. Макарова 542
- НВ 778
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1992
- НГУЭУ 499
- НИИ 201
- ОмГТУ 301
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 119
- РАНХиГС 186
- РОАТ МИИТ 608
- РТА 243
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 122
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 130
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1598
- СПбГТИ (ТУ) 292
- СПбГТУРП 235
- СПбГУ 577
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 193
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 113
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2423
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 324
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 306
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
Группы компаний по основным производственным фондам, млн. руб. (х)
Число компаний (fi)
Середина интервала (Xi) = (начало интервала+конец интервала)/2
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.


Далее рассчитаем среднюю взвешенную величину.


Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
Число компаний (f)
Середина интервала (Xi) = (начало интервала+конец интервала)/2
При статистической обработке итогов изысканий самого различного рода полученные значения зачастую группируются в последовательность промежутков. Для расчета обобщающих колляций таких последовательностей изредка доводится вычислять середину интервала – «центральную варианту». Способы ее расчета довольно примитивны, но имеют некоторые особенности, вытекающие как из применяемой для измерения шкалы, так и из нрава группировки (открытые либо закрытые промежутки).
Инструкция
1. Если промежуток является участком постоянной числовой последовательности, то для нахождения ее середины используйте обыкновенные математические способы вычисления среднеарифметического значения. Минимальное значение интервала (его предисловие) сложите с максимальным (окончанием) и поделите итог напополам – это один из методов вычисления среднеарифметического значения. Скажем, это правило применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, потому что (21+33)/2=27.
2. Изредка бывает комфортнее применять иной способ вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте вначале определите ширину диапазона – отнимите от максимального значения минимальное. После этого поделите полученную величину напополам и прибавьте итог к минимальному значению диапазона. Скажем, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, потому что 47,15+(31,98/2) = 47,15+15,99 = 63,14.
3. Если промежуток не является участком обыкновенной числовой последовательности, то вычисляйте его середину в соответствии с повторяемостью и размерностью применяемой измерительной шкалы. Скажем, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
4. Помимо обыкновенных (закрытых) промежутков статистические способы изысканий могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Скажем, открытый промежуток может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется способом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют идентичную ширину, то предполагается, что и данный открытый промежуток имеет такую же размерность. В отвратном случае вам нужно определить динамику метаморфозы ширины промежутков, предшествующих открытому, и вывести его условную ширину, исходя из полученной склонности метаморфозы.
Изредка в повседневной деятельности может появиться надобность обнаружить середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия либо легко распилить на две равные части деревянный брусок. На поддержка приходит геометрия и немножко житейской смекалки.
Вам понадобится
- Циркуль, линейка; булавка, карандаш, нить
Инструкция
1. Воспользуйтесь обыкновенными инструментами, предуготовленными для измерения длины. Это самый легкой метод разыскать середину отрезка. Измерьте линейкой либо рулеткой длину отрезка, поделите полученное значение напополам и отмерьте от одного из концов отрезка полученный итог. Вы получите точку, соответствующую середине отрезка.
2. Существует больше точный метод нахождения середины отрезка, вестимый из курса школьной геометрии. Для этого возьмите циркуль и линейку, причем линейку может заменить всякий предмет подходящей длины с ровной стороной.
3. Установите расстояние между ножками циркуля так, дабы оно было равным длине отрезка либо же огромным, чем половина отрезка. После этого поставьте иглу циркуля в один из концов отрезка и проведите полуокружность так, дабы она пересекала отрезок. Переставьте иглу в иной конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность верно таким же образом.
4. Вы получили две точки пересечения полуокружностей по обе стороны от отрезка, середину которого мы хотим обнаружить. Объедините эти две точки при помощи линейки либо ровного бруска. Соединительная линия пройдет в точности посередине отрезка.
5. Если под рукой не оказалось циркуля либо длина отрезка значительно превышает возможный размах его ножек, дозволено воспользоваться простым приспособлением из подручных средств. Изготовить его дозволено из обыкновенной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немножко превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Довольно верно обнаружить середину доски либо бруска вы можете, использовав обыкновенную нитку либо шнур. Для этого отрежьте нить так, дабы она соответствовала длине доски либо бруска. Остается сложить нить верно напополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а 2-й конец будет соответствовать его середине.
Функция ОТРЕЗОК
В этой статье описаны синтаксис формулы и использование функции ОТРЕЗОК в Microsoft Excel.
Описание
Вычисляет точку пересечения линии с осью y, используя значения аргументов «известные_значения_x» и «известные_значения_y». Точка пересечения находится на оптимальной линии регрессии, проведенной через точки, заданные аргументами «известные_значения_x» и «известные_значения_y». Функция ОТРЕЗОК используется, если нужно определить значение зависимой переменной при нулевом значении независимой переменной. Например, с помощью функции ОТРЕЗОК можно предсказать электрическое сопротивление металла при температуре 0°C, если имеются данные измерений при комнатной температуре и выше.
Синтаксис
Аргументы функции ОТРЕЗОК описаны ниже.
Известные_значения_y — обязательный аргумент. Зависимое множество наблюдений или данных.
Известные_значения_x — обязательный аргумент. Независимое множество наблюдений или данных.
Замечания
Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
Если аргументы «известные_значения_y» и «известные_значения_x» содержат разное количество точек данных или вовсе не содержат точек данных, функция ОТРЕЗОК возвращает значение ошибки #Н/Д.
Уравнение для точки пересечения линии линейной регрессии a с осью y имеет следующий вид:
где наклон b вычисляется следующим образом:
где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).
Алгоритм, лежащий в основе работы функций ОТРЕЗОК и НАКЛОН, отличается от алгоритма, на котором основана функция ЛИНЕЙН. Результаты вычислений по этим алгоритмам могут не совпадать в случае неопределенных и коллинеарных данных. Например, если точками данных аргумента «известные_значения_y» являются нули, а аргумента «известные_значения_x» — единицы, то справедливо указанное ниже.
От ПЕРЕХВАТ и НАКЛОН возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритмы ОТОКП и НАКЛОН предназначены для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.
Функция ЛИНЕЙН возвратит нулевое значение. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Середина отрезка. Координаты середины отрезка
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A( xa , ya ) и B( xb , yb ) на плоскости:
| xc = | xa + xb | yc = | ya + yb |
| 2 | 2 |
Формула вычисления координат середины отрезка с концами A( xa , ya , za ) и B( xb , yb , zb ) в пространстве:
| xc = | xa + xb | yc = | ya + yb | zc = | za + zb |
| 2 | 2 | 2 |
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если у вас есть два списка дат, теперь вы хотите найти дату середины между заданными двумя датами, как бы вы могли это сделать?
Вычислить данные середины между двумя заданными датами с помощью формулы
Вычислить данные середины между двумя заданными датами с помощью формулы
Чтобы получить дату середины между двумя заданными датами, вам может помочь следующая формула. Пожалуйста, сделайте так:
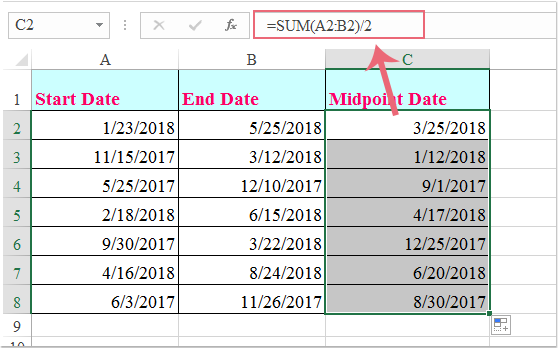
Введите эту формулу: =SUM(A2:B2)/2 в пустую ячейку, в которую вы хотите вывести результат, а затем перетащите дескриптор заполнения вниз к ячейкам, к которым вы хотите применить эту формулу, и вся средняя дата была рассчитана, как показано на следующем снимке экрана:
Внимание: В приведенной выше формуле A2 это дата начала, а B2 дата окончания, вы можете изменить их по своему усмотрению.
Лучшие инструменты для работы в офисе
Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%
- Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
- Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
- Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
- Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
- Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
- Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
- Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
- Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
- Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.
Вкладка Office: интерфейс с вкладками в Office и упрощение работы
- Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
- Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
- Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!
Комментарии (1)
Оценок пока нет. Оцените первым!
Количественные данные следует определить как «Числовые».
2.
Для выполнения расчета необходимо
закрыть имеющиеся открытые интервалы – первый – «до 500», последний — «от 700».
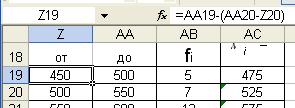
Формула вычисления левой границы первого интервала вводится в
ячейку Z19 : «=АА19-(АА20-Z20)»
(– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
Правая граница последнего интервала в ячейку АА23 устанавливается
формулой «=Z23+АА22-Z22» (от
значения в ячейке Z23 откладывается размер
предшествующего интервала «АА22-Z22»).
3.

каждой группе , как
середина интервала. Для этого в ячейку первой группы (АС19) устанавливается функция
СРЗНАЧ(Z19;AA19). После появления среднего значения первого интервала формула
копируется в соседние ячейки. При этом автоматически смещаются координаты
исходных данных в соответствии со смещением координат ячейки результата.
4.
Рассчитывается величина средней
взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель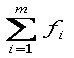
«/» — знак деления.
Дисперсия. Среднее
квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут
вычисляться по простой и взвешенной формулам.
Дисперсия, среднее
квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel
используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором
возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и
СКО зарплаты подразделения:
1.
Исходные значения признака хi надо
записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
2.
В ячейку результата дисперсии (например
«AF44») установить функцию ДИСПР(AF42:AQ42)
1.
В ячейку результата СКО (например
«AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Знак «^0,5» — означает возведение в степень 0,5 величины стоящей
перед ним.
Дисперсия,
среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel
используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
оператор «/».
СКО определяется как квадратный корень дисперсии, реализуемый оператором
возведения в степень «^».

методику расчета на примере расчета дисперсии и СКО размера семьи группы
1.
Исходные значения признака хi и
частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в
примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
1.
Рассчитать среднее арифметическое
взвешенное — в примере в ячейке AW49 установлена формула =СУММПРОИЗВ (AT46:AY46;AT47:AY47)/СУММ(AT47:AY47)
Перейти к содержанию
На чтение 1 мин. Просмотров 32 Опубликовано 24.05.2021
Если у вас есть два списка дат, теперь вы хотите найти дату середины между заданными двумя датами, как бы вы могли это сделать?
Вычислить данные середины между двумя заданными датами с помощью формулы
Вычислить данные середины между двумя заданными датами с формулой

Потрясающе! Использование эффективных вкладок в Excel, таких как Chrome, Firefox и Safari!
Сэкономьте 50% своего времени и уменьшите тысячи щелчков мышью каждый день!
Чтобы получить дату середины между двумя заданными датами, вам может помочь следующая формула. Пожалуйста, сделайте следующее:
Введите эту формулу: в пустую ячейку, в которую вы хотите вывести результат, а затем перетащите дескриптор заполнения вниз к ячейкам, которые вы хотите применить эту формулу, и вся средняя дата была рассчитана, как показано на следующем снимке экрана:

Примечание . В приведенной выше формуле A2 – это дата начала, а B2 – это дата окончания, вы можете изменить их по своему усмотрению.
- MID в Excel
Функция MID в Excel (Содержание)
- MID в Excel
- MID Formula в Excel
- Как использовать функцию MID в Excel?
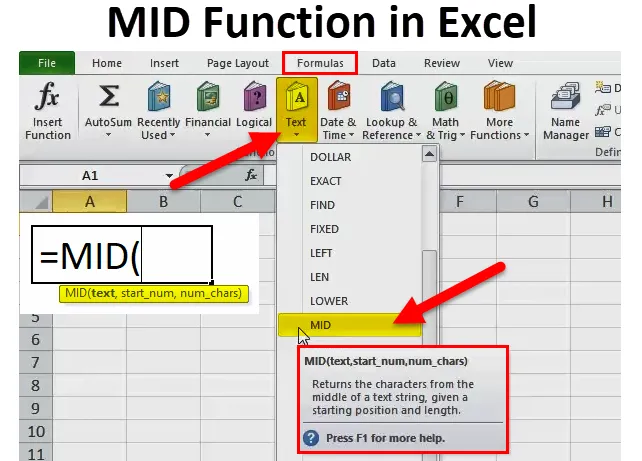
MID в Excel
Функция MID в Excel является частью текстовой функции. Функция MID полезна, когда вы хотите вернуть указанное количество символов текста.
Проще говоря, функция MID используется для извлечения небольшой части строки из входной строки или возврата необходимого количества символов из текста или строки.
Например:
MID («Бангалор — столица штата Карнатака», 18, 7) в этой формуле функция MID возвращает из 18- го символа, возвращает 7 символов, то есть «Столица» .
Функция MID также доступна в VBA. Мы обсудим это в конце этой статьи.
MID Formula в Excel
Ниже приведена формула MID в Excel:
Объяснение формулы MID в Excel
Формула MID имеет три обязательных параметра: ietext, start_num, num_chars.
- текст: из текста, который вы хотите извлечь указанные символы.
- start_num: начальная позиция средней строки.
- (num_chars): количество символов, которое вы хотите извлечь из начального номера .
Обычно функция MID в Excel используется наряду с другими текстовыми функциями, такими как ПОИСК, ЗАМЕНА, ЛЕН, НАЙТИ, ВЛЕВО и т. Д.
Как использовать функцию MID в Excel?
Функция MID в Excel очень проста и удобна в использовании. Давайте рассмотрим работу функции MID в Excel на примере MID Formula.
Вы можете скачать этот шаблон Excel с функцией MID здесь — Шаблон Excel с функцией MID
Функция MID может использоваться как функция рабочего листа и как функция VBA.
Пример № 1
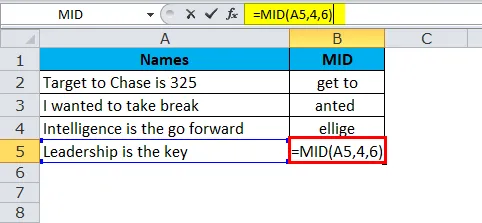
В этом примере формулы MID в Excel мы извлекаем подстроку из заданной текстовой строки, используя формулу MID.
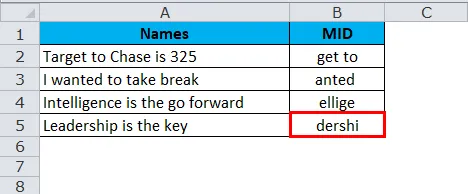
Из таблицы, приведенной выше, символы из 4- го символа извлекают 6 символов.
Итак, результатом будет:
Пример № 2
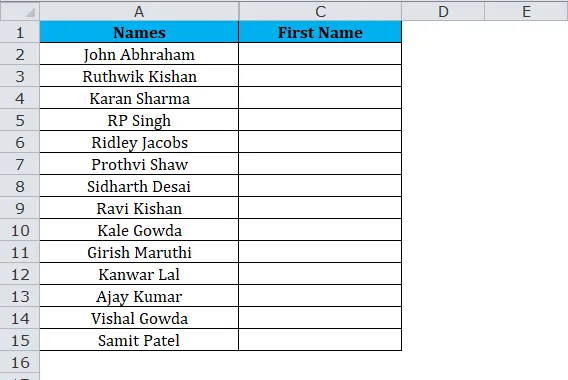
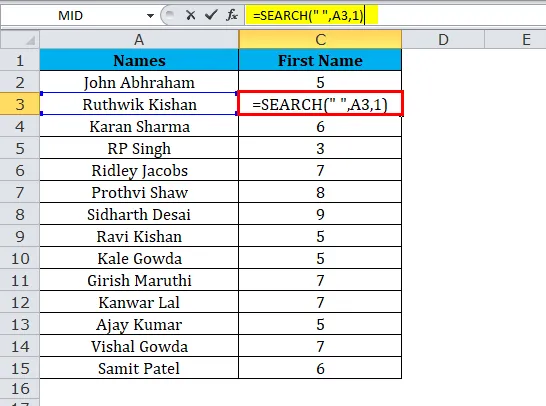
Используя функцию MID, мы можем извлечь имя и фамилию. Посмотрите на приведенный ниже пример, где у нас есть полные имена от А2 до А15.
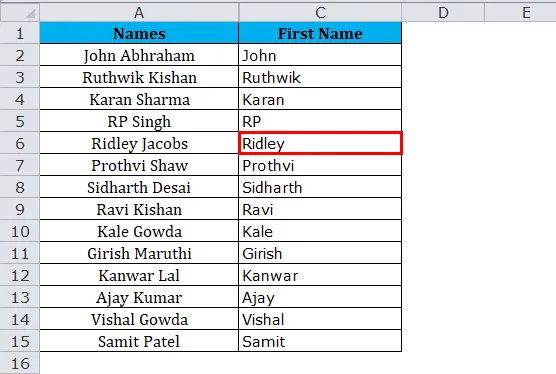
Из приведенной выше таблицы извлеките имена для всех имен.
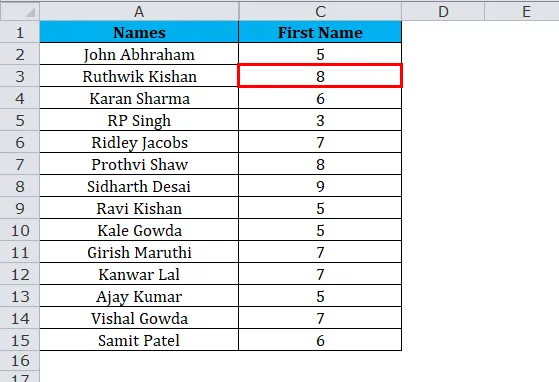
Результат:
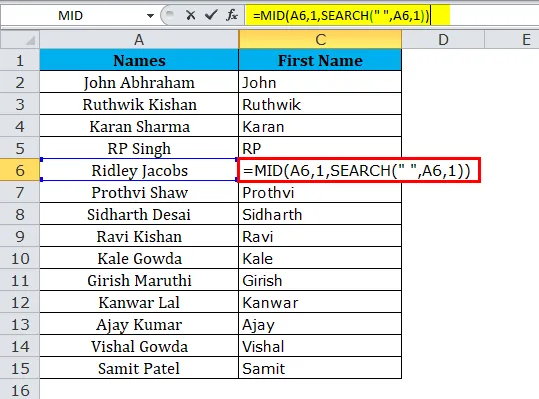
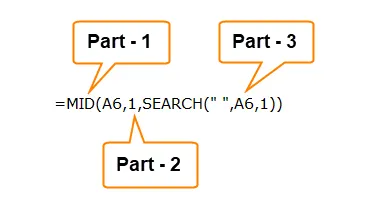
Часть 1: эта часть определяет желаемый текст, который вы хотите извлечь символы.
Часть 2: Это определяет начальную позицию персонажа.
Часть 3: Функция ПОИСК ищет первый пробел («») в тексте и определяет расположение пробела.
Здесь формула SEARCH возвращает 5 для имени, которое означает, что пробел является 5- м символом в вышеприведенном тексте. Теперь функция MID извлекает 5 символов, начиная с 1- го .
Итак, результатом будет:
Примечание: пробел также считается одним символом.
Пример № 3
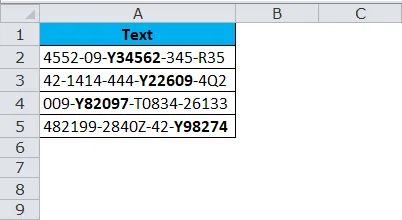
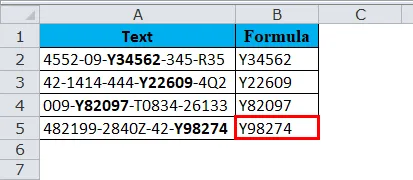
Ниже приведен список номеров рейсов, и нам нужно извлечь символы, начиная с Y, до тех пор, пока вы не найдете « — »
Посмотрите на приведенный выше пример, где буквы выделены жирным шрифтом, который мы должны извлечь. Выглядит чертовски из задачи, не так ли ?
Однако мы можем сделать это, используя MID вместе с функциями SEARCH или FIND.
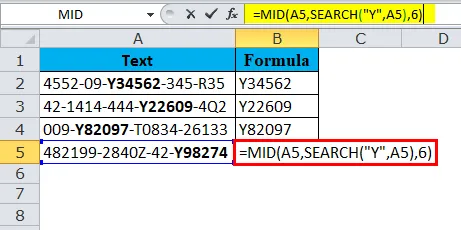
Общеизвестно, что все жирные буквы начинаются с буквы Y и имеют всего 6 символов.
Функция SEARCH определит начальный символ для извлечения, и из начальной точки нам нужно извлечь 6 символов.
Итак, результат:
Пример № 4
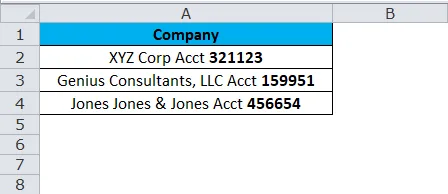
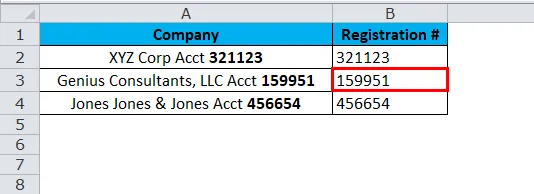
Ниже приведен список компаний вместе с их регистрационным номером. Задача — извлечь из списка только регистрационный номер.
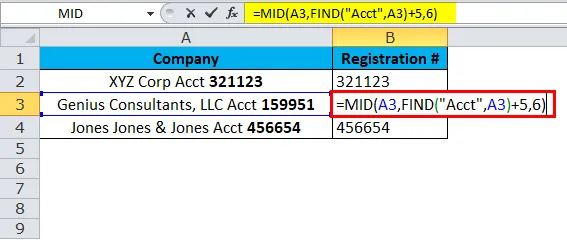
Внимательно посмотрите на приведенный выше список одной общей вещи, прежде чем регистрационный номер является словом Acct. Это будет нашей ключевой точкой для определения отправной точки. В предыдущем примере мы использовали SEARCH, на этот раз мы рассмотрим функцию FIND.
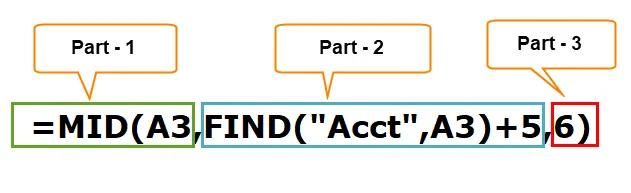
Часть 1: эта часть определяет желаемый текст, который вы хотите извлечь символы.
Часть 2: Функция НАЙТИ сначала ищет слово « Acct » в тексте, и оттуда нам нужно добавить еще 5 символов в список, которые определяют начальную позицию символа.
Мы должны добавить 5, потому что от Acct до регистрационного номера это 5 символов, включая пробел.
Часть 3: Количество символов, которые мы должны извлечь.
Итак, результатом будет:
Пример № 5
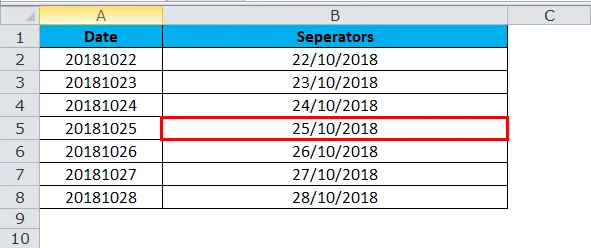
Теперь мы рассмотрим комбинацию функций RIGHT, LEFT и MID в одном примере. Нам нужно объединить косую черту (/) для разделения года, месяца и дня.
Посмотрите на приведенный ниже пример, где у нас есть даты, но нет разделителей для года, месяца и дня.
Теперь нам нужно вставить разделители для года, месяца и дня.
Во-первых, функция RIGHT извлекает 2 символа справа и вставляет одну косую черту (/), т.е. 25 /
Теперь нам нужно вставить разделители для года, месяца и дня.
Вторая часть — это функция MID, которая извлекает 2 символа, начиная с 5- го символа, и вставляет одну косую черту (/)
т.е. 25/10 /
Последняя часть — функция LEFT, которая извлекает 4 символа слева и вставляет одну косую черту (/)
то есть 25/10/2018
Итак, результатом будет:
Код VBA для использования функции MID
Как и в Excel, мы можем использовать функцию MID в коде VBA. Код ниже иллюстрирует использование функции MID в макросах VBA.
Sub MID_Function_Example Dim Middle_String в виде строки Middle_String = Mid («Excel может творить чудеса», 14, 7) Msgbox Middle_String End Sub
Если вы запустите приведенный выше код, в окне сообщения будут отображаться чудеса.
Что нужно помнить о функции MID в Excel
- Форматирование чисел не является частью строки и не будет извлечено или подсчитано.
- Это предназначено для извлечения символов с любой стороны указанного текста.
- Если пользователь не указывает последний параметр, он по умолчанию принимает 0.
- Num_chars должно быть больше или равно нулю. Если это отрицательное число, оно выдаст ошибку как # ЗНАЧЕНИЕ.
- В случае сложных наборов данных вам необходимо использовать другие текстовые функции, такие как SEARCH, параметр FIND Num_chars.
- Используйте функцию MID, когда вы хотите извлечь текст из текстовой строки, в зависимости от местоположения и длины.
- Функция MID возвращает пустой текст, если start_num больше длины строки.
Рекомендуемые статьи
Это было руководство по MID в Excel. Здесь мы обсуждаем формулу MID в Excel и как использовать функцию MID в Excel вместе с практическими примерами и загружаемыми шаблонами Excel. Вы также можете просмотреть наши другие предлагаемые статьи —
- Использование функции AND в Excel
- Лучшие примеры функции COLUMN в Excel
- Функция LOOKUP в Excel
- Удивительное использование функции FV в Excel
- Как использовать функцию MID в VBA?
Не трудно. Но решение не блещет гибкостью.
Ещё раз хочется разъяснить задачу, т.к. в прошлый раз я, возможно, недостаточно полно её описал.
Генерирую отчёт в Excel. Использую свой компонент на основе TExcelApplication и шаблоны. Отчёты получаются небольшие, т.е. умещаются на половине листа. По заданию необходимо делать копию полученной «верхней» части отчёта внизу таким образом, чтобы лист можно было разрезать пополам и части получились бы одинаковые половинки. Надеюсь понятно написал ). Найти какие либо св-ва и методы, позволяющие получить строку, указывающую на середину печатаемой области листа мне не удалось. А без этой строки, ясно дело, я не могу скопировать содержимое «верха» по ценру листа.
Решил проблему дубово. Посчитал количество пикселей до середины листа в самом шаблоне (пусть будет H), и после формирования «верха» выполняю поиск номера строки считая сумму высот строк H[i] пока не дойду до H. i и будет искомая строка. Проблема в том, что такой способ годится только для жёстко заданных шаблонов, т.е. если вы что-то в нём сменили(например, поля), придётся менять исходник, что есть ОЧЕНЬ плохо, т.к. я именно от этого и хотел отказаться.
Вообще цель моих изысканий заключается в том, чтобы минимально менять код, а максимально всё делать в шаблоне. Если кто знает хорошую литературу, не поскупитесь, киньте ссылку. Закрытые компоненты не интересуют. Заранее спасибо.
Решение статистических задач в EXCEL: Практикум , страница 3
Количественные данные следует определить как «Числовые».
2. Для выполнения расчета необходимо закрыть имеющиеся открытые интервалы – первый – «до 500», последний — «от 700».
Формула вычисления левой границы первого интервала вводится в ячейку Z19 : «=АА19-(АА20-Z20)» (– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
Правая граница последнего интервала в ячейку АА23 устанавливается формулой «=Z23+АА22-Z22» (от значения в ячейке Z23 откладывается размер предшествующего интервала «АА22-Z22»).
3. 
4. Рассчитывается величина средней взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель;
«/» — знак деления.
Дисперсия. Среднее квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут вычисляться по простой и взвешенной формулам.
Дисперсия, среднее квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО зарплаты подразделения:
1. Исходные значения признака хi надо записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
2. В ячейку результата дисперсии (например «AF44») установить функцию ДИСПР(AF42:AQ42)
1. В ячейку результата СКО (например «AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Знак «^0,5» — означает возведение в степень 0,5 величины стоящей перед ним.
Дисперсия, среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».

1. Исходные значения признака хi и частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
1. Рассчитать среднее арифметическое взвешенное — в примере в ячейке AW49 установлена формула =СУММПРОИЗВ (AT46:AY46;AT47:AY47)/СУММ(AT47:AY47)
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
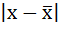 |
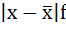 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
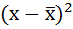 |
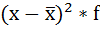 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Как найти середину?
Чтобы найти середину, нарисуйте числовую линию, содержащую точки и. Затем рассчитайте расстояние между двумя точками. В этом случае расстояние между и составляет. Разделив расстояние между двумя точками на 2, вы установите расстояние от одной точки до средней точки.
Тем не менее, как найти середину?
Чтобы найти середину любого диапазона, сложите два числа и разделите на 2. В этом случае 0 + 5 = 5, 5/2 = 2.5.
следующий: как найти середину интервала?
Разделите сумму верхнего и нижнего пределов на 2.. Результат — середина интервала. В этом примере 12, разделенное на 2, дает 6 как среднюю точку между 4 и 8.
тогда какова середина между двумя числами?
Середина между двумя числами — число точно посередине двух чисел. Вычисление средней точки — это то же самое, что вычисление среднего двух чисел. Следовательно, вы можете вычислить среднюю точку между любыми двумя числами, сложив их вместе и разделив на два.
Какова формулировка теоремы о средней точке?
Теорема о средней точке утверждает, что «Отрезок в треугольнике, соединяющий середину двух сторон треугольника, считается параллельным его третьей стороне и также составляет половину длины третьей стороны.«.
Как найти середину частотного распределения?
«Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Какова середина академического интервала?
«Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Что вы называете серединой урока?
Знак класса определяется как среднее значение нижнего и верхнего пределов. Следовательно, средняя точка интервала между занятиями называется отметкой класса.
Какая средняя точка гистограммы?
На полпути между соседними интервалами реальные пределы интервала, которые определяют, где конкретная точка данных будет «подсчитана» на гистограмме. Например, обратите внимание на третью полосу на этой гистограмме. Средняя точка равна 5. Нижний реальный предел находится на полпути между 2.5 и 5, или 3.75.
Какая средняя точка 25 и 50?
Таким образом, число, находящееся посередине между 25 и 50, равно 37.5. Как видите, среднее число на 12.5 больше, чем 25, и на 12.5 меньше, чем 50. Таким образом, наш средний ответ 37.5 выше правильный.
Какая средняя точка 15 и 20?
Когда вы спрашиваете: «Какое число находится посередине между 15 и 20?» мы предполагаем, что вы имеете в виду число точно посередине двух чисел на числовой строке, как показано ниже, где X = 15 и Y = 20. Таким образом, число, находящееся на полпути между 15 и 20, равно 17.5. Как видите, среднее число на 2.5 больше 15 и 2.5 меньше 20.
Как найти середину частотного распределения?
Вы можете добавить дополнительную информацию в свою таблицу распределения частот. «Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Как работает формула средней точки?
Средняя точка M тогда определяется как М = ((х + Х) / 2, (у + Y) / 2). … Чтобы показать, что M действительно является средней точкой отрезка PQ, нам нужно показать, что расстояние между M и Q такое же, как расстояние между M и P, и что это расстояние составляет половину расстояния от P до Q.
Какая середина треугольника?
Середина треугольника — это отрезок, соединяющий середины двух сторон треугольника. На рисунке D — это середина ¯AB, а E — середина ¯AC. Итак, ¯DE — это мидсегмент.
Как проверить теорему о средней точке?
Математические лаборатории с активным отдыхом — проверьте теорему о средней точке
- ЗАДАЧА.
- Теория. Теорема о средней точке: отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне.
- Процедура. Шаг 1. Наклейте на картон один лист белой бумаги. …
- Наблюдения.
- Результат. Теорема о середине проверена.
В чем разница между теоремой о средней точке и ее определением?
В чем разница между теоремой о средней точке и ее определением? Определение: для данного сегмента линии существует середина. Теорема: средняя точка делит отрезки на два равных отрезка. Определение: высоты треугольника пересекаются в общей точке, называемой ортоцентром.
Что такое середина статистики?
Гистограмма, показывающая средние точки. Средняя точка класса (или отметка класса) — это определенная точка в центре интервалов (категорий) в таблице частотного распределения; Это также центр полосы на гистограмме. … Средняя точка определяется как среднее значение верхнего и нижнего пределов класса.
Как найти середину гистограммы?
Полигон частот можно создать из гистограммы или путем вычисления средних точек интервалов из таблицы распределения частот. Средняя точка бункера рассчитывается по формуле сложение верхнего и нижнего граничных значений ячейки и деление суммы на 2.
Как найти середину учебного интервала?
Для нахождения середины интервала классов мы используем формулу: Средняя точка = нижний предел класса + верхний предел класса 2 а для нахождения диапазона данных мы должны найти разницу между наивысшим и наименьшим баллами.
Какова середина интервала 10 класса?
Size = 20-10 = 10. Следовательно, размер интервала каждого класса равен 10. Следовательно, средняя точка класса 30-40 равна
35
. Диапазон = 64-12 = 52.
| Интервал класса | Счетные отметки | частота |
|---|---|---|
| 10-20 | |||| | 9 |
| 20-30 | 12 | |
| 30-40 | ||| | 8 |
| 40-50 | || | 7 |
Какая средняя точка у класса 15-20?
Отметка класса также известна как средняя точка класса — это особая точка в середине интервала классов. он определяется выражением, где a = нижний предел и b = верхний предел. Таким образом, размер класса и оценка класса 15-20 составляет 5 и 17.5.
Какова средняя точка доверительного интервала?
Важной темой в статистике является доверительный интервал, который сообщает нам наиболее вероятный интервал, в котором будет находиться среднее значение или пропорция. Часто дается нижняя и верхняя границы доверительного интервала, но средняя точка этих двух чисел является наилучшим предположением. для того, что мы ищем.
Какая средняя точка в таблице частот?
Средние значения точки: средние числа в каждой из групп. Самый простой способ найти их — сложить верхнюю и нижнюю границы и разделить ответ на два. Последний столбец находится путем умножения средней точки на частоту. Например, 1250 х 9 = 11250.
Что такое мидпойнт в статистике?
Средняя точка класса (или отметка класса) — это определенная точка в центре интервалов (категорий) в таблице частотного распределения; Это также центр полосы на гистограмме. Посмотрите видео, чтобы узнать, как рассчитать отметки / середины классов:… Средняя точка определяется как среднее значение верхнего и нижнего пределов класса.
Как найти середину сгруппированных данных?
Чтобы найти средние точки, сложите начальную и конечную точки, а затем разделите на 2. Середина 0 и 4 равна 2, потому что. Мы не знаем точное значение каждого из 11 элементов данных в группе 0 <m ≤ 4, поэтому лучшая оценка, которую мы можем сделать, состоит в том, что каждый элемент данных был равен средней точке, 2.
Какая середина класса высшего класса?
Нижний предел для каждого класса — это наименьшее значение в этом классе. С другой стороны, верхний предел для каждого класса является наибольшим значением в этом классе. Средняя точка класса нижний предел класса плюс верхний предел класса, деленный на 2.
Excel is mostly about numerical, however, we often have data of text data type. Here are a few functions we should know to handle text data.
- LEFT
- RIGHT
- MID
- LEN
- FIND
The LEFT function
The LEFT function returns a given text from the left of our text string based on the number of characters specified.
Syntax:
LEFT(text, [num_chars])
Parameters:
- Text: The text we want to extract from.
- Num_chars (Optional): The number of characters you want to extract. Default num_chars is 1 and the number must be a positive number that is greater than zero.
Example:
Step 1: Format your data.
Now if you want to get the first “Geeks” from “Geeksforgeeks” in B2. Let us follow the next step.
Step 2: We will enter =LEFT(B2,5) in the B3 cell. Here we want Excel to extract the first 5 characters from the left side of our text in B2.
This will return “Geeks”.
The RIGHT Function
The RIGHT function returns a given text from the left of our text string based on the number of characters specified.
Syntax:
RIGHT(text, [num_chars])
Parameters:
- Text: The text we want to extract from.
- Num_chars (Optional): The number of characters you want to extract. Default num_chars is 1 and the number must be a positive number that is greater than zero.
Example:
Step 1: Format your data.
Now if you want to get the last geeks from “Geeksforgeeks” in B2. Let us follow the next step.
Step 2: We will enter =RIGHT(B2,5) in the B3 cell. Here we want Excel to extract the last 5 characters from the right side of our text in B2.
This will return “geeks”.
The MID function
The MID function returns the text from any middle part of our text string based on the starting position and number of characters specified.
Syntax:
MID(text, start_num, num_chars)
Parameters:
- Text: The text we want to extract from.
- start_num: The starting number of the first character from the text we want to extract.
- Num_chars: The number of characters you want to extract.
Example:
Step 1: Format your data.
Now if you want to get the character “for” which is located in the middle of our text “Geeksforgeeks” in B2. Let us follow the next step.
Step 2: We will enter =MID(B2,5,3) in the B3 cell. Here we want Excel to extract the characters located in the middle of our text in B2.
This will return “for”.
The Len Function
The LEN function returns the number of characters in the text strings.
Syntax:
LEN(text)
Parameters:
- Text: The text we want to know the length
Example:
Step 1: Format your data.
Now if you want to know how many characters are in the text “Geeksforgeeks”. Let us follow the next step.
Step 2: We will enter =LEN(B2) in the B3 cell. Excel will count how many characters are in the text.
This will return 13.
The FIND Function
The FIND function returns the position of a given text within a text.
Syntax:
FIND(find_text, within_text, [start_num])
Parameters:
- Find_text: The text we want to find.
- Within_text: The text containing our find_text.
- Start_num (Optional): The starting position of our find_text. Default is 1.
Example:
Step 1: Format your data.
Now if you want to find “for” in geeksforgeeks in B2. Let us follow the next step.
Step 2: We will enter =FIND(“for”,B2) in B3 cell. Here we want Excel to find “for” in our text in B2.
This will return 6 because “for” is located at character number 6 in our text.