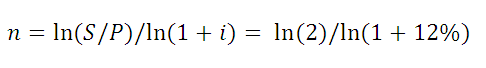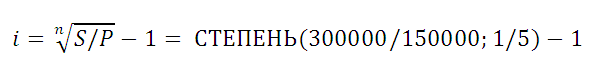Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.
Немного теории
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по
простым
и сложным процентам.
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
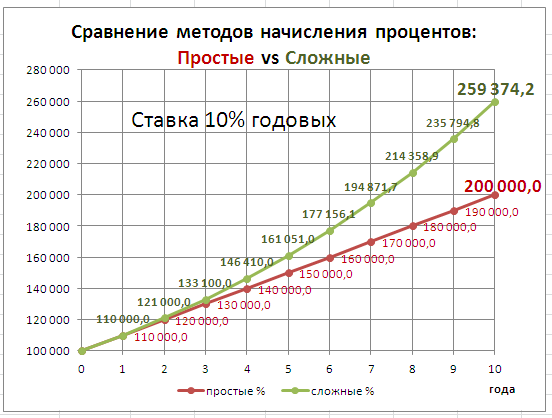
В
файле примера
приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.
В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов
читайте здесь
.
Начисление процентов 1 раз в год
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.
Начисление процентов несколько раз в год
В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).
В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.
Рассмотрим задачу
: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.
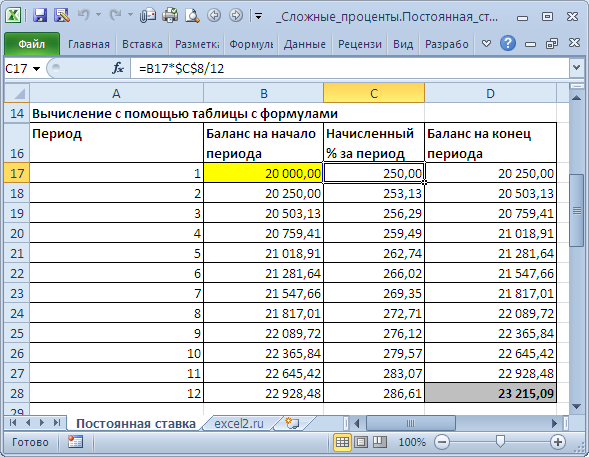
Способ 1. Вычисление с помощью таблицы с формулами
Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В
файле примера
это реализовано на листе
Постоянная ставка
.
За первый период будут начислены проценты в сумме
=20000*(15%/12)
, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.
Способ 2. Вычисление с помощью формулы Наращенных процентов
Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию
СТЕПЕНЬ()
=20000*СТЕПЕНЬ(1+15%/12; 12)
Способ 3. Вычисление с помощью функции БС().
Функция
БС()
позволяет определить
будущую стоимость
инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае
аннуитетных платежей
. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.
=-БС(15%/12;12;;20000)
Или так
=-БС(15%/12;12;0;20000;0)
Примечание .
В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов
используется функция
БЗРАСПИС()
.
Определяем сумму начисленных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.
Сумма начисленных процентов I равна разности между величиной наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.
файл примера
).
Определяем Срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.
В
файле примера
приведено решение, ответ 6,12 лет.
Вычисляем ставку сложных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?
В
файле примера
приведено решение, ответ 14,87%.
Примечание
. Об эффективной ставке процентов
читайте в этой статье
.
Учет (дисконтирование) по сложным процентам
Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.
Математический учет
. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.
Пример
. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .
Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв
сегодня
вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.
Тот же результат можно получить с помощью формулы
=ПС(15%;7;;-2000000;1)
Функция
ПС()
возвращает приведенную (к текущему моменту) стоимость инвестиции и
рассмотрена здесь
.
Банковский учет
. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи
Начисление процентов несколько раз в год
.
Расчет сложных процентов в случае регулярного пополнения вклада
В
файле примера
(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция
БС()
.
Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.
|
высчитывание ежедневного процента |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
17 авг. 2022 г.
читать 2 мин
Мы можем использовать следующую формулу, чтобы найти конечную стоимость некоторых инвестиций через определенное время:
A = P(1 + r/n) нт
куда:
- A: Окончательная сумма
- P: Начальный основной
- r: Годовая процентная ставка
- n: количество периодов начисления сложных процентов в год.
- т: количество лет
Если инвестиции начисляются ежедневно , то мы можем использовать 365 для n :
А = Р(1 + г/365) 365t
В следующем примере показано, как использовать эту формулу в Excel для расчета конечной стоимости некоторых инвестиций, которые ежедневно начисляются.
Пример: ежедневная формула сложных процентов в Excel
Предположим, мы инвестируем 5000 долларов в инвестиции, которые начисляются по ставке 6% в год. Предположим, что инвестиции складываются ежедневно.
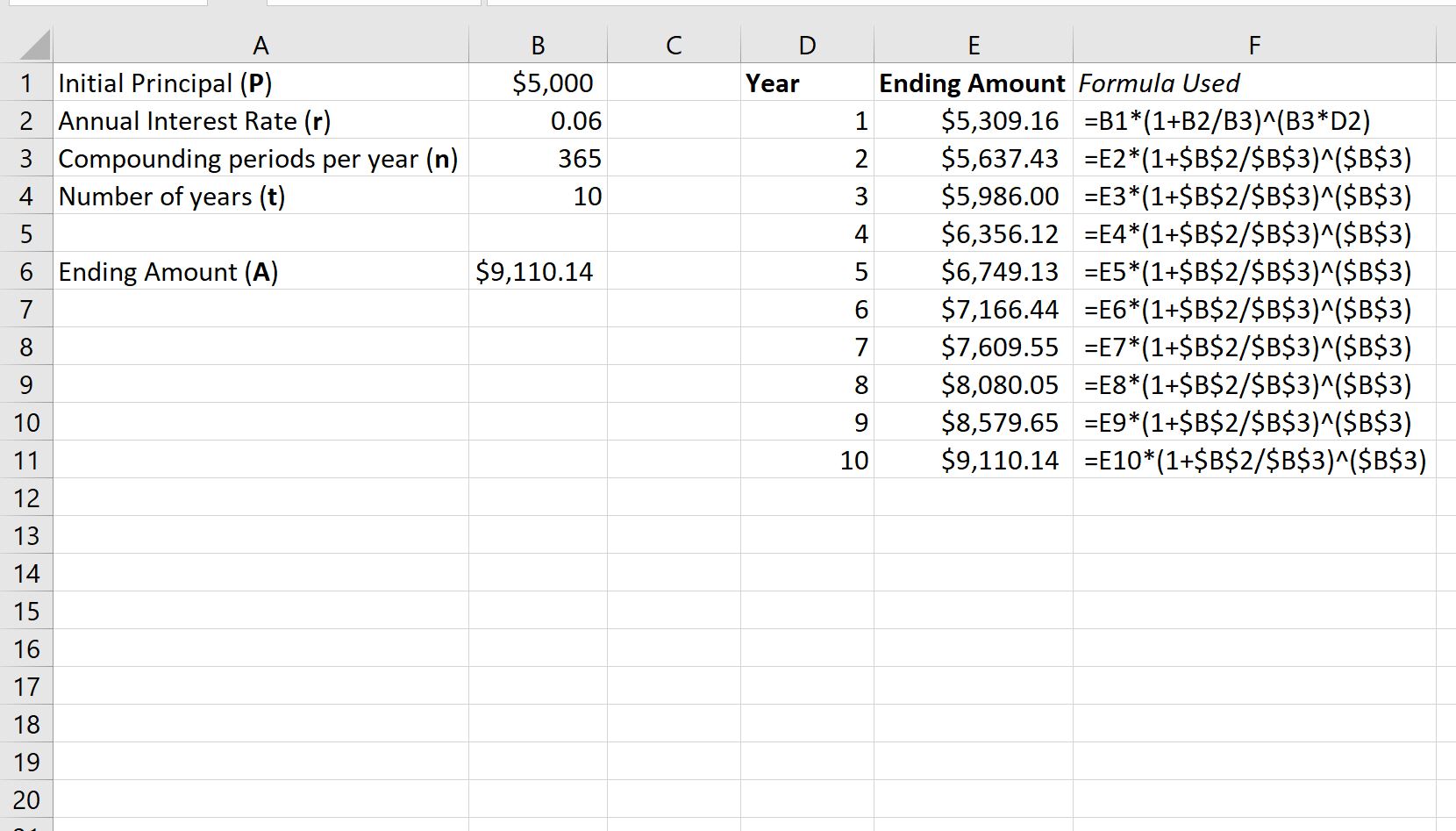
На следующем снимке экрана показано, как использовать формулу сложных процентов в Excel для расчета конечной стоимости этих инвестиций через 10 лет:
Эта инвестиция будет стоить 9 110,14 долларов США через 10 лет.
На следующем снимке экрана показано, как рассчитать конечные инвестиции после каждого года в течение 10-летнего периода.
Примечание.В столбце F показана формула, которую мы использовали в каждой соответствующей ячейке столбца E:
Из вывода мы видим:
- В конце первого года инвестиции составляют 5 309,16 долларов США .
- В конце 2-го года инвестиции составляют 5 637,43 доллара .
- В конце 3-го года инвестиции составляют 5 986,00 долларов США .
А к концу 10 года инвестиции составляют 9 110,14 долларов .
Чтобы визуализировать рост инвестиций с течением времени, просто выделите ячейки в диапазоне E2:E11 , затем щелкните вкладку « Вставка » на верхней ленте, затем выберите параметр « Двухмерная столбчатая диаграмма » в группе « Диаграммы »:
Ось X показывает год, а высота столбцов представляет собой стоимость инвестиций в конце каждого года.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как найти антилог значений в Excel
Как решить систему уравнений в Excel
Как рассчитать сводку из пяти чисел в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
First, calculating interest on your bank account daily makes the most sense because your balance in a bank account typically fluctuates throughout the month: that is, you make deposits, and you make withdrawals.
If the bank calculated interest only at the end of the month, say, based on your balance at that point in time, then it might not be fair to either you or the bank. Depending on whether your end-of-month balance was higher than average, or lower than average, either you or the bank would come out ahead. So, by calculating interest daily the bank is, in effect, arriving at an amount of interest on some form of average balance, which is more fair to both of you.
However, even though interest may be calculated daily, it is typically only credited to your account once per month. Imagine the mess it would make on your statement if it were credited daily!
Regarding calculating interest in Excel, have a look at the EFFECT() function. See also How to calculate compound interest for an intra-year period in Excel. For instance, if the nominal annual interest rate were 5% and you wanted to know what the effective annual interest rate is with monthly compounding, you would write =EFFECT(0.05,12), which would yield 0.051161898, or ~5.116%.
A longer form in lieu of the Excel EFFECT() function is what you’ll find explained at Wikipedia — Credit card interest — Calculation of interest rates, i.e. the EAR = (1 + APR/n)^n -1 formula. Or, in Excel, =POWER(1+0.05/12,12)-1 to match the example above. Also yields 0.051161898.
However, each of the methods above to compute the effective annual interest rate is only appropriate if you want to know the future value some years hence but without any inflows or outflows. Once you have a situation where you are making deposits or withdrawals, you’ll want to create a spreadsheet that calculates the daily interest and adds it to the ongoing balance on a monthly frequency.
To arrive at the actual amount of interest you would need to accrue for a single day, you would divide the original interest rate by 360 or 365. (Bank rules on this may vary – I’m not exactly sure.) So, the daily interest on a balance of, say, $1000 would be =1000*0.05/365, yielding 0.13698630 or 14 cents if rounded up to the nearest penny. Of course, you need to know the rounding rules. Perhaps rounding is done on each day’s resulting interest (before summing), or on the sum of the month’s resulting interest. Plus, bankers can round different than you might expect. Again, I’m not exactly sure on this.
In constructing a spreadsheet to calculate interest this way, you should not be adding the daily interest to the ongoing balance directly, but rather accrue the interest in a separate spot off to the side somewhere until the end of the month. At which point, sum up all of the daily interest earned and add it to the ongoing balance. Consider: If you were to credit the ongoing balance each day with that day’s interest, then you would, in effect, be performing daily compounding instead. By adding the interest to the ongoing balance only once per month, the compounding is in effect monthly, even though the interest is calculated on the daily balance.
Here’s a link to a sample Excel spreadsheet (*.xlsx) I created to demonstrate the above.
Excel 2016 Excel 2013 Office для бизнеса Excel 2010 Еще…Меньше
Сводка
Будущая стоимость суммы в рублях, обычно называемая составной стоимостью, включает применение составных процентов к сумме к сумме к настоящей стоимости. Результатом будет будущая сумма в рублях. Три типа составных соединений
год, интра-год и составные аннуитеты. В этой статье рассмотрены вычисления в течение года по сложным интересам.
Дополнительные сведения о ежегодном соединении можно получить в следующей статье:
БС
Вычисление будущей стоимости Intra-Year сложных процентов
Intra-year compound interest is interest that is compounded more frequently than once a year. Финансовые учреждения могут вычислять проценты на основе полугодных, квартальных, ежемесячных, еженедельных и даже ежедневных периодов времени.
Microsoft Excel включает функцию ЭФФЕКТ в надстройку «Надстройка анализа» для более старых версий, чем 2003. Уже загружено средство анализа. Функция ЭФФЕКТ возвращает составную процентную ставку на основе годовой процентной ставки и количества периодов в году.
Формула для вычисления в течение года сложных процентов с помощью функции ЭФФЕКТ:
=P+(P*EFFECT(EFFECT(k,m)*n,n))
Общее уравнение для вычисления составных процентов
=P*(1+(k/m))^(m*n)
где верно следующее:
P = начальная основной
k = уплаченная годовая процентная ставка
m = количество раз за период (как правило, месяцы) проценты являются составными
n = количество периодов (обычно лет) или срок займа
Примеры
В примерах этого раздела используются функция ЭФФЕКТ, общая формула и данные из следующего примера:
|
Intra-Year сложные ставки |
Количество периодов в году, за которые начисляются сложные проценты |
|---|---|
|
Полугодовой |
2 |
|
Ежеквартально |
4 |
|
Ежемесячно |
12 |
|
Еженедельно |
52 |
|
Ежедневно |
360 или 365 (фактические) |
Инвестиция в размере 100 долларов США оплачивает 8,00 % составных полугов. Если деньги остались на счете в течение трех лет, сколько будет стоить 100 рублей?
Использование функции «Эффект»
Для вычисления полугодных периодов составных периодов необходимо дважды повторить функцию ЭФФЕКТ. В следующем примере результат вложенной функции умножается на 3, чтобы распределить (раз в год) составную ставку в течение срока инвестиции:
=100+(100*EFFECT(EFFECT(.08,2)*3,3))
В примере возвращается $126,53.
Использование общей формулы
В следующем примере используется общая формула:
=100*(1+.08/2)^(2*3)
В примере возвращается $126,53.
Расчет процентных ставок для Intra-Year сложных процентов
Вы можете найти составную процентную ставку по годовой процентной ставке и сумме в рублях.
Функция ЭФФЕКТ использует следующую формулу:
=EFFECT(EFFECT(k,m)*n,n)
Чтобы использовать общую формулу для возврата составной процентной ставки, используйте следующее уравнение:
=(1+(k/m))^(m*n)-1
Примеры
Использование функции «Эффект»
Инвестиция в размере 100 долларов США оплачивает 7,50 % составных ежеквартов. Например, деньги будут слева на счете в течение двух лет. Следующая формула возвращает составную процентную ставку:
=EFFECT(EFFECT(.075,4)*2,2)
В примере возвращается 16,022 процента.
Использование общей формулы
Следующая формула возвращает процентную ставку:
=(1+(.075/4))^(4*2)-1
Ссылки
Чтобы получить дополнительные сведения о составных интересах, щелкните Microsoft Excel Справка в меню Справка, введите эффект в помощнике по Office или мастере ответов, а затем нажмите кнопку Поиск, чтобы просмотреть раздел.