Excel для математического моделирования

Цели урока:

1. Обучающие: Повторить и закрепить навыки
   работы в MS Excel; научить применять современное
   программное обеспечение в решении
   математических задач, строить математические
   модели в среде MS Excel.




2. Развивающие: Развивать: практические и
   исследовательские навыки по составлению моделей
   в электронных таблицах, научное мировоззрение
   через связь информационных технологий с другими
   школьными предметами, логическое и
   алгоритмическое мышление, аналитические
   способности, внимание, память.




3. Воспитательные: Воспитание общей и
   информационной культуры, творческого подхода к
   работе, желания экспериментировать,
   самостоятельности в учебном труде.

• компьютеры с ОС MS Windows XP;

• пакет Microsoft Office;

• мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

1. Орг. момент. (1 мин)
2. Проверка и актуализация знаний. / Тестирование
   по теме (4 мин)./ Разминка (5 мин)
3. Теоретическая часть. (10 мин)
4. Практическая часть. (10 мин)
5. Самостоятельная работа. (8 мин)
6. Подведение итогов. Д/з (2 мин)

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

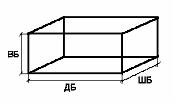
Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

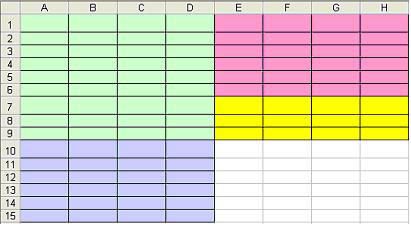
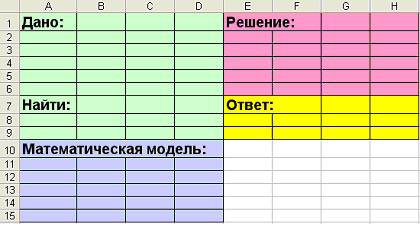
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

 Заполнить таблицу начальными
данными.

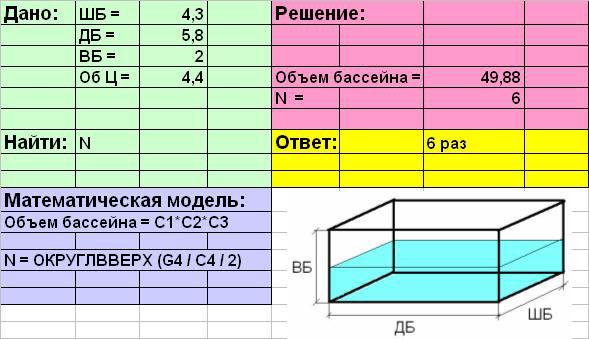
В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

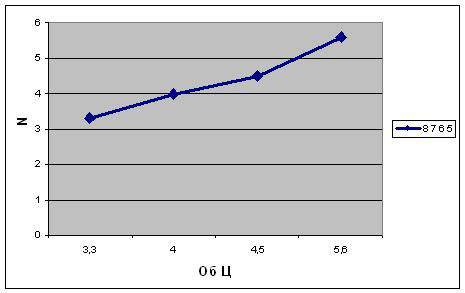
 Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

 Анализ полученных результатов.

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

1. Назвать лист номером задачи «Задача 2»
   (редактирование названия – двойной щелчок мыши
   на «Лист 2»).
2. Выделить расчетную таблицу на листе «Задача1»
   и скопировать ее на лист «Задача 2«.
3. Заполнить таблицу новыми начальными данными.
4. Ввести формулу (тип данных – текст) в раздел
   «Математическая модель» (пробел перед
   знаком «=»).
5. Ввести фоpмулу (тип данных – формулы) в
   раздел «Решение«.
6. В разделе «Ответ» записать искомый
   результат (тип данных – текст).




7. Создать таблицу значений t и занести в нее
   результаты вычислений S. Заполнить таблицу
   данными.
8. Для графического представления результатов
   выделить область аргументов и функций, построить
   график зависимости пути S от времени при t=40;60;90,
   отредактировать график.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Федеральное
агентство по образованию

ГОУ ВПО «Российский
государственный профессионально–педагогический

университет»

Уральское отделение
Российской академии образования

Академия
профессионального образования

Екатеринбург

2007

УДК

ББК

Г

Городецкая
Н.В.
Математическое моделирование в MS
Excel:
Учеб. пособие. Екатеринбург: Изд-во ГОУ
ВПО «Рос. гос. проф.-пед. ун-т», 2007. 64 с.

Учебное пособие
содержит лабораторные работы,
ориентированные на знакомство с одной
из технологий – математическое
моделирование на основе среды Microsoft
Excel.

Лабораторные
работы включают необходимый теоретический
материал и непосредственные инструкции
по освоению математического моделирования
в среде Microsoft
Excel.

Пособие может быть
использовано для преподавания дисциплины
«Математическое моделирование» у
студентов специальности
050501 Профессиональное обучение
(информатика, вычислительная техника
и компьютерные технологии) (030500.06),
специализации «Компьютерные технологии».

Практикум подготовлен
при финансовой поддержке Российского
гуманитарного научного фонда в рамках
научно–исследовательского проекта
«Психолого–педагогические и
технологические условия применения
адаптивных методических систем в
дистанционных образовательных
технологиях» (№ 06−06−00475а).

Рецензенты: д-р
физ.-мат. наук, проф. В.Е. Третьяков
(ГОУ ВПО «Уральский государственный
университет»); д-р пед. наук, проф. Л.И.
Долинер (ГОУ ВПО «Российский
государственный профессионально-педагогический
университет»)

© ГОУ ВПО 
«Российский

государственный
профессионально-

педагогический
университет», 2007

© Н.В. Городецкая,
2007

Оглавление

Преподавателю:
как использовать это пособие 4

Тому,
кто хочет научиться 4

Введение 5

Лабораторная
работа 1 7

Лабораторная
работа 2 26

Лабораторная
работа 3 33

Лабораторная
работа 4 47

Лабораторная
работа 5 56

Литература 64

Преподавателю: как использовать это пособие

Данная
серия лабораторных работ предназначена
для знакомства обучаемых с технологией
использования математического
моделирования для решения задач. В
качестве конкретного инструментального
средства выбрана среда MicrosoftExcel.

Для
использования данного пособия в обучении
необходимо:

1. иметь
   дискету, прилагаемую к пособию, для
   установки рабочих файлов (без них работа
   с пособием невозможна);

2. установить
   на компьютере полную версию MicrosoftExcel(с возможностью
   осуществлятьПоиск решения);

3. создать
   (в случае отсутствия) в корневом каталоге
   одного из дисков папку Учебнаяи
   скопировать в папкуУчебнаяпапкуМАТ_МОД, содержащую учебные файлы
   с прилагаемой дискеты.

Тому, кто хочет научиться

Если
Вы решили с помощью этого пособия
познакомиться с технологией использования
математического моделирования в среде
MicrosoftExcel,
рекомендуется:

1. расположиться
   перед включенным компьютером с
   установленной полной версией MicrosoftExcel;

2. выполнять
   лабораторные работы как можно более
   точно, поскольку тексты лабораторных
   работ представляют собой в некотором
   роде инструкции, соблюдение которых
   обеспечит Вам успешную и комфортную
   работу;

3. соблюдать
   следует следующие правила:

1. текст,
   который никак не выделен, следует только
   читать;

2. определения,
   отмеченные значком
   ,
   необходимо запомнить;

3. обращать
   внимание на текст, помеченный значком
   ;

4. практические
   задания, отмеченные словом «Задание»,
   следует обязательно и в полном объеме
   выполнять на компьютере;

5. контрольные
   задания следует также выполнять
   самостоятельно; если Вы справитесь с
   ними без помощи преподавателя, это
   означает, что Вы усвоили материал;

6. на
   контрольные вопросы нужно отвечать
   устно – они подготовят Вас к компьютерным
   тестовым вопросам;

7. для
   повторения пройденного материала
   следует использовать резюме;

1. делать
   краткий конспект — это поможет Вам
   ускорить усвоение материала;

2. отвечать
   на все вопросы, приведенные в конце
   каждой лабораторной работы;

3. приглашать
   преподавателя тогда, когда это
   предлагается сделать в тексте лабораторной
   работы;

4. если
   Вы занимаетесь без преподавателя,
   выполняйте полностью все задания
   лабораторных работ, отвечайте устно
   на вопросы.

В книге
приняты следующие обозначения:

—
этот символ используется для выделения
определений;

—
так помечаются важные замечания;

—
резюме;

—
при встрече с таким символом следует
пригласить преподавателя (консультанта)
и показать ему результаты выполнения
заданий. Если Вы работаете самостоятельно,
просто пропустите текст, помеченный
этим символом;

ЛП– линейное программирование; ЦФ–
целевая функция;

РЗ– распределительная задача; ТЗ–
транспортная задача.

Соседние файлы в папке Исслед_опер

• #

  24.04.201517.92 Кб148lab_3(b).xls

• #

  24.04.201517.92 Кб88lab_3(а).xls

• #

  24.04.201527.14 Кб114lab_4(a).xls

• #

  24.04.201523.04 Кб91lab_4(b).xls
• #

  24.04.201519.97 Кб143lab_5.xls

• #

Работа:

Использование табличного процессора MS Excel и математического моделирования для решения математических задач

Цель работы: Исследовать
возможность моделирования исследование математических функций, при помощи
современных компьютерных средств. Методы проведенных исследований:
математическое моделирование. Основные результаты научного исследования
(научные, практические): разработана компьютерная модель для исследования 
математических функций на основе программы Microsoft Excel .

актуальность темы работы
– Microsoft Excel — одна из самых загадочных и интересных программ в пакете MS
Office. Интересна она многочисленными средствами автоматизации работы,
оформления документов и богатыми вычислительными возможностями. Загадочность ее
состоит в том, что большинство пользователей применяют лишь малую толику того,
что может дать им Excel. Это тем более удивительно, что спектр возможностей
программы практически безграничен: от создания простых таблиц, построения
диаграмм и графиков до решения сложных вычислительных задач и моделирования
различных процессов.

постановка и формулировка проблемы – данная работа посвящена использованию электронных таблиц EXCEL в
анализе функций. В ней, используя знания и навыки работы с мастером функций и
диаграмм Excel, будет проведен анализ  функций с проведением расчетов по
формулам и с построением графиков.
Для анализа элементарных функций необходимо уметь решать следующие задачи:

• определение
  возрастания или убывания функции на заданном интервале,
• определение
  максимума (минимума) данной функции на заданном интервале,
• нахождение
  точек пересечения функции с осью ОХ,
• нахождение
  производной функции

1. При решении некоторых задач часто возникает
необходимость использования последовательности чисел.

-Правка

-Заполнить

-Прогрессия (показать)

От 1 до 10

Вносим формулу n/(n+1)

Копируем, замечаем, что при возрастании n
, последовательность n/(n+1) стремиться к 1, при n=10000000, уже равна 1.

2Данную программу можно использовать для
решения систем линейных уравнений.

— Прогрессия От-2 до 2 с шагом 0,2 задаем х.

-Выразим у и внесем в соседние ячейки,
скопируем.

— Построим график

-Уточним решение:

Внесем полученный ответ, т.е. (0;2) в
некоторые ячейки, В27:С27

Ниже внесем формулы функций с ссылкой на
аргумент т. на В27  и минус значение функции т.е. С27. по адресам В30:В32

Сервис, Поиск Решения, Установить Целевую
ячейку В30=0, изменяя наши результаты, указываем диапазон В27:С27, и
ограничения В31=0 и В3=0

3. В нахождении
корней функции   с помощью Прогрессии заполняем значения аргумента с шагом 0,1
на отрезке от -1 до 1

В соседнюю ячейку формулу функции с ссылкой на
значение аргумента и копируем.

Видим, что функция меняет знак с минуса на
плюс три раза. Выбираем значения.

Уточняем их с помощью:

Сервис, Параметры, Вычисления, Автоматически, количество интераций 1000 (Итерация в программировании —
организация обработки данных, при которой действия повторяются многократно),
погрешность 0,000001.

Сервис , Подбор параметра:

4. Находить экстремум функции или наибольшее и
наименьшее значения.

Возьмем любое значение х из отрезка от -2 до
2, ну например -0,8

В соседнюю ячейку введем формулу функции с
ссылкой на это значение аргумента

Сервис, Поиск решения, установить целевой ячейкой ячейку в нашем случае В3 = минимальному
значению (Изменяя ячейку А3, и ограничения указываем отрезок, А3.>=0, A3<=0, Выполнить

Получим

. Проверим правильно ли найдено решение
задания

С помощью Прогрессии заполняем значение х  на
от -2 до 2  с шагом 0,1.

В соседнюю ячейку внесем формулу функции 
ссылкой на значение аргумента.

Выделим ячейки у и с помощью функции минимум
(Вставка, Функция) найдем минимум  1,75

В частном случае при нахождении экстремума на
указанном отрезке, найденное значение может быть не минимумом (максимумом)
функции, а просто минимальным (максимальным) значением на указанном отрезке, т.е.
экстремумом являться не будет. Чтобы проверить, является ли найденное
решение экстремумом функции, необходима дополнительная проверка с помощью
вычисления производной функции. Если производная функции для найденного решения
равна нулю, то точка является экстремумом, а не точкой
перегиба функции.

Производная – это отношение малого приращения
функции к малому приращению аргумента.

В ячейку Е2=А3+1Е-9  т.е. к ячейке
А3+0,000000001

В ячейку Е3 =А3-1Е-9 т. е. от ячейки
А3-0,000000001, т.е. наше приращение аргумента величина 0,000000001 (Уточним
количество знаков после запятой- Формат, Ячейки, Числовой- укажем 10 знаков
после запятой)

В ячейку F2 внесем
формулу функции с ссылкой на ячейку Е2, и аналогично в ячейку F3 внесем формулу функции с ссылкой на ячейку Е3.

В ячейку G2 формулу =(F3-F2)/(E3-E2)  и когда производная будет равна нулю, тогда наша точка будет
экстремумом.

                                                        
Заключение
            В настоящее время получило всеобщее признание то, что успех развития
многих областей науки и техники существенно зависит от развития многих
направлений математики. Математика становится средством решения проблем
организации производства, поисков оптимальных
решений.                                      

            Программа

Microsoft Excel – одна из наиболее
практически значимых, востребованных.  Электронные таблицы не только позволяют
автоматизировать расчеты, но и являются эффективным средством моделирования
различных вариантов и ситуаций. Меняя значения исходных данных, можно
проследить за изменением получаемых результатов и из множества вариантов
решения задачи выбрать наиболее подходящий.