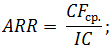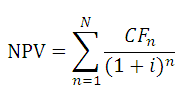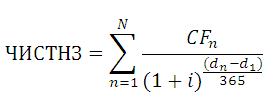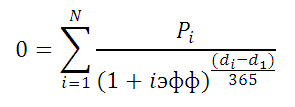Excel для инвестиционных расчетов

Для привлечения и вложения средств в какое-либо дело инвестору необходимо тщательно изучить внешний и внутренний рынок.

На основании полученных данных составить смету проекта, инвестиционный план, спрогнозировать выручку, сформировать отчет о движении денежных средств. Наиболее полно всю нужную информацию можно представить в виде финансовой модели.

Финансовая модель инвестиционного проекта в Excel

Составляется на прогнозируемый период окупаемости.

Основные компоненты:

• описание макроэкономического окружения (темпы инфляции, проценты по налогам и сборам, требуемая норма доходности);
• прогнозируемый объем продаж;
• прогнозируемые затраты на привлечение и обучение персонала, аренду площадей, закупку сырья и материалов и т.п.;
• анализ оборотного капитала, активов и основных средств;
• источники финансирования;
• анализ рисков;
• прогнозные отчеты (окупаемость, ликвидность, платежеспособность, финансовая устойчивость и т.д.).

Чтобы проект вызывал доверие, все данные должны быть подтверждены. Если у предприятия несколько статей доходов, то прогноз составляется отдельно по каждой.

Финансовая модель – это план снижения рисков при инвестировании. Детализация и реалистичность – обязательные условия. При составлении проекта в программе Microsoft Excel соблюдают правила:

• исходные данные, расчеты и результаты находятся на разных листах;
• структура расчетов логичная и «прозрачная» (никаких скрытых формул, ячеек, цикличных ссылок, ограниченное количество имен массивов);
• столбцы соответствуют друг другу;
• в одной строке – однотипные формулы.



Расчет экономической эффективности инвестиционного проекта в Excel

Для оценки эффективности инвестиций применяются две группы методов:

• статистические (PP, ARR);
• динамические (NPV, IRR, PI, DPP).

Срок окупаемости:

Коэффициент PP (период окупаемости) показывает временной отрезок, за который окупятся первоначальные вложения в проект (когда вернутся инвестированные деньги).

Экономическая формула расчета срока окупаемости:

где IC – первоначальные вложения инвестора (все издержки),

CF – денежный поток, или чистая прибыль (за определенный период).

Расчет окупаемости инвестиционного проекта в Excel:

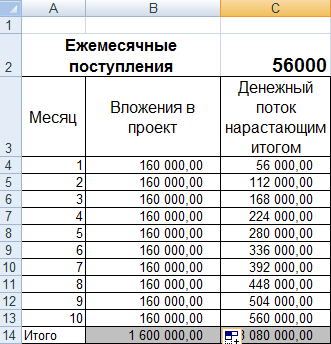
1. Составим таблицу с исходными данными. Стоимость первоначальных инвестиций – 160000 рублей. Ежемесячно поступает 56000 рублей. Для расчета денежного потока нарастающим итогом была использована формула: =C4+$C$2.



2. Рассчитаем срок окупаемости инвестированных средств. Использовали формулу: =B4/C2 (сумма первоначальных инвестиций / сумма ежемесячных поступлений).

Так как у нас дискретный период, то срок окупаемости составит 3 месяца.

Данная формула позволяет быстро найти показатель срока окупаемости проекта. Но использовать ее крайне сложно, т.к. ежемесячные денежные поступления в реальной жизни редко являются равными суммами. Более того, не учитывается инфляция. Поэтому показатель применяется вкупе с другими критериями оценки эффективности.

Рентабельность инвестиций

ARR, ROI – коэффициенты рентабельности, показывающие прибыльность проекта без учета дисконтирования.

Формула расчета:

где CFср. – средний показатель чистой прибыли за определенный период;

IC – первоначальные вложения инвестора.

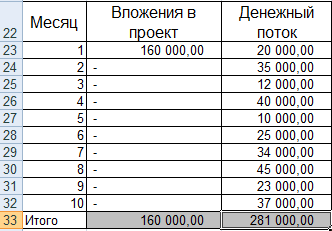
Пример расчета в Excel:

1. Изменим входные данные. Первоначальные вложения в размере 160 000 рублей вносятся только один раз, на старте проекта. Ежемесячные платежи – разные суммы.



2. Рассчитаем средние поступления по месяцам и найдем рентабельность проекта. Используем формулу: =СРЗНАЧ(C23:C32)/B23. Формат ячейки с результатом процентный.

Чем выше коэффициент рентабельности, тем привлекательнее проект. Главный недостаток данной формулы – сложно спрогнозировать будущие поступления. Поэтому показатель часто применяется для анализа существующего предприятия.

Примеры инвестиционне6ого проекта с расчетами в Excel:

• скачать полный инвестиционный проект
• скачать сокращенный вариант в Excel

Статистические методы не учитывают дисконтирование. Зато позволяют быстро и просто найти необходимые показатели.

Инвестиционная модель в EXCEL с NPV-анализом

Уважаемые посетители!
Перечень всех финансовых и инвестиционных моделей нашего сайта, которые можно бесплатно скачать,
Вы найдете здесь.

В современном социуме вопросы финансовой безопасности как отдельного человека – физического лица, так и каждого предприятия –
юридического лица в структуре жизненно важных приоритетов находятся далеко не на последних местах.
Долгосрочный стабильный прирост капитала обеспечивает при прочих равных условиях уверенность в завтрашнем дне
и готовность ко многим форс-мажорным происшествиям, влекущим потребность в финансовых средствах для их нейтрализации, конечно же,
когда речь не идет о глобальных потрясениях.

По отношению к уже накопленному капиталу задачей-минимум, которую решает его обладатель, является сохранение капитала.
Где под «сохранением капитала» мы понимаем сохранение его рыночной ликвидности во времени, т.е., если на данный момент
времени преобразовав весь свой капитал в максимально возможный относительно рыночной конъюнктуры объем денежных средств
(в чистые финансы), обладатель этого капитала делает все возможное, чтобы и через год и через десять лет его капитал
оценивался или, что тоже самое, мог быть конвертирован на рынке в такой же или больший объем денежных средств, но только
не с точки зрения номинала (суммы), а сточки зрения покупательной способности в натуральных объемах некоторой
«продуктовой корзины», ну, или, по крайней мере, с точки зрения официальной инфляции.

Наиболее доступный способ, к которому прибегают, чтобы сохранить капитал в виде денежных средств,
это положить деньги в банк на депозит. Но по известным причинам в надежных банках процент по депозитам обычно не
покрывает инфляцию, а в ненадежных банках можно просто потерять весь капитал. Поэтому при таком способе долгосрочного
сохранения капитала необходимо иметь дополнительные источники дохода, которые будут покрывать потери капитала в связи
с инфляцией, т.е. необходима постоянная «подпитка капитала извне».

Но пожалуй, более заманчивой, а возможно и более популярной формой не только сохранения капитала, но и его преумножения
являются инвестиции, о чем в данном разделе и пойдет речь.

Пример реально действующей системы комплексного инвестиционного анализа и комплексной оценки финансово-хозяйственного
состояния предприятия или будущего инвестиционного проекта/стартапа с расчетом всех ключевых финансовых и инвестиционных показателей,
а также оценки стоимости бизнеса или компании в целом можно посмотреть, скачав универсальную финансовую модель поколения 4.0
для анализа всевозможных инвестиционных проектов и принятия решений об инвестировании в них ниже в синей рамке.

СКАЧАТЬ


ФИНМОДЕЛЬ С ИНВЕСТИЦИОННЫМ АНАЛИЗОМ БИЗНЕС-ПРОЕКТА

Для целей настоящей статьи под инвестициями или инвестиционными вложениями мы будем понимать направление капитала в
виде денежных средств в производственную инфраструктуру с целью создания в будущем серийного производства нового продукта
или расширения производства для создания бОльшего объема продукции, и через продажу которой предполагается возврат вложенных
инвестиционных средств. Где в свою очередь в качестве производственной инфраструктуры будем рассматривать все составляющие
цикла создания продукта потребления от идей, научных исследований и проектных работ до разработки, строительства,
внедрения и запуска мощностей серийного производства и сбыта.

Как обычно, сразу выкладываем для скачивания соответствующую финансовую модель инвестиционного проекта (инвестмодель)
в виде EXCEL-файла:

СКАЧАТЬ


Классическая базовая инвестиционная модель

Чтобы на начальном этапе знакомства с методами инвестиционного анализа не перегружать читателя разнообразной спецификой типов
объектов капитальных вложений, представленный для скачивания EXCEL-файл содержит, так сказать, базовую инвестиционную модель
схематичного вида, где капитальные вложения рассматриваются, как простой инвестиционный поток во времени.

Для удобства ознакомления и в качестве примера данная инвестмодель уже наполнена конкретными данными исходных финансово-экономических
показателей, которые пользователь вносит для расчета ключевых показателей эффективности инвестиционного проекта.
Эта же модель, но только незаполненная, приведена в виде такого же EXCEL-файла для скачивания в конце раздела.

Прежде чем перейти к описанию финмодели инвестиционного проекта, для полноты содержания раздела «управление финансами»
мы познакомим с основными широко известными и подробно представленными, например, в Интернете показателями эффективности
инвестиционных проектов такими, как NPV, IRR, PP, PI, ROI и т.д., а также коснемся принципов достаточно нового современного
подхода к управлению коммерческой структурой, который носит емкую аббревиатуру «EVA» — Economic Value Added;
авторами концепции EVA являются американцы Б.Стюарт и Д.Стерн.

Для любого инвестора при вложении денег в тот или иной проект, инвестиционный проект, естественно важно, чтобы,
как минимум, произошел возврат инвестиционных вложений в полном объеме и более того, чтобы возврат этого самого «полного объема»
был произведен, как в народе говорят, «с учетом стоимости денег» или, как говорят, специалисты «с учетом уровня потери
покупательной способности денежных средств».

Учет покупательной способности денег в инвестиционном анализе происходит путем введения коэффициента дисконтирования,
с помощью которого производится дисконтирование будущих финансовых потоков или, что тоже самое, приведение финансового потока будущих
периодов к некоторому определенному моменту времени, например, к моменту начала инвестиционного проекта.

Чтобы понять, как работает дисконтирование разберемся сначала с процессом того, как происходит изменение покупательной
способности денежных средств. Допустим, Вы ходите в магазин и покупаете систематически за 1000руб. один и тот же набор товаров,
составляющих Вашу собственную «потребительскую корзину», т.е. Ваш средний чек на протяжении некоторого периода времени равен 1000руб.
Далее пусть также по прошествии еще некоторого периода времени происходят изменения цен на товары Вашей потребительской корзины и
Вам приходится покупать тот же набор товаров уже за 1100руб., т.е. на 10% дороже. Тогда если предположить, что у Вас нет 1100руб.
на покупку полной корзины, а Вы все также располагаете ровно «той же» тысячью рублей, тогда Вы сможете купить лишь только некоторую долю,
обозначим ее через D, от той продуктовой корзины, которую привыкли покупать до повышения цен. И эта доля, как легко посчитать, равна

D = 1 / (1 + 10%).

То есть покупательная способность денег относительно Вашей продуктовой корзины или Ваша личная покупательская способность снизилась на

10% / (1 + 10%) = 9,(09)%.

Получается, что инфляция в размере 10% «съедает» чуть более 9% Вашей продуктовой потребительской корзины.
Или обобщая, получаем, что при Вашем финансовом бездействии в течение инфляционного периода инфляция в размере i процентов «съест»

i * D(i) * 100%

процентов Ваших повседневных потребительских возможностей, которыми Вы обладаете в настоящий момент, где

D(i) = 1 / (1 + i).

Значит, если не бездействовать с точки зрения Вашего финансового положения, т.е. для того чтобы иметь и в будущем возможность
потреблять на том же уровне, Вам необходимо позаботиться о том, чтобы либо Ваш доход (например, заработная плата)
со временем увеличился на инфляционный процент, либо Ваши накопления прирастали со скоростью инфляции.
На самом деле и то и другое означает создание условий, при которых прирост Вашего капитала в широком смысле будет не ниже уровня инфляции,
ведь получая заработную плату, Вы взамен отдаете свой «трудовой капитал».

В случае же если деньги есть сейчас, а потратить их придется в будущем через определенный срок, тогда необходимо найти такую
возможность вложить эти денежные средства, чтобы через этот срок они не потеряли покупательную способность.
Например, если банк предлагает процент по депозиту на указанный срок в размере ожидаемой инфляции по продукции,
которую предполагается купить по истечение срока, то при понятных рисках можно положить деньги на депозит в этот банк.
Но, как мы уже заметили выше, такое положение дел встречается крайне редко.

Для нас же здесь важным является то, что при вложении свободных денежных средств сегодня в какой-либо (долгосрочный) проект
инвестор должен рассчитать/оценить будущий возврат вложенных средств, как минимум, с точки зрения потери покупательной способности.
Или, говоря научным языком, необходимо продисконтировать будущий финансовый поток инвестиционного проекта
(без учета возврата инвестиционных вливаний), тем самым, привести все движения денежных средств в рамках одноименного отчета
финансовой модели инвестпроекта к настоящему моменту, после чего сравнить итог с вложенной суммой инвестиций, также приведенной
к настоящему моменту, в случае если инвестиционные вложения происходят не единовременно в начальный момент,
а как-то распределены в рамках периода реализации проекта (в соответствии с графиком инвестирования).

Классическая формула такого расчета, а именно расчета приведенного к настоящему моменту финансового потока инвестиционного п
роекта без учета возврата инвестиционных вливаний имеет следующий вид:

PV = ∑_t=1,2,…,n CF_t / (1 + d)^t.

Здесь через PV (Present Value) обозначен приведенный к «настоящему» моменту (моменту начала инвестиционного проекта) объем
финансового потока инвестпроекта. Через CF_t обозначена величина финансового потока периода t в номинале, которая в
свою очередь равна разнице между притоком CF⁺_t и оттоком CF^—_t
денежных средств (ДС) за период t при реализации проекта:

CF_t = CF⁺_t — CF^—_t, для каждого t=1,2,…,n.

Наконец через d мы обозначили ставку дисконтирования, выражаемую в процентах, и через n – количество базовых периодов,
на которые разделен период реализации (рассмотрения реализации) нашего инвестиционного проекта.

Для простейшей оценки состоятельности или просто окупаемости проекта очевидно, что необходимо произвести сравнение полученной
приведенной стоимости PV инвестпроекта с объемом инвестиционных вложений в него, также приведенных к начальной точке проекта –
обозначим приведенный инвестиционный поток через PIV или, что тоже самое, необходимо сравнить разницу между PV и PIV с нулем.
Эта разница между приведенным (дисконтированным) финансовым потоком проекта и соответствующим инвестиционным потоком обычно
обозначается через NPV и называется чистой приведенной стоимостью проекта или чистым дисконтированным доходом проекта,
и имеет свое выражение в виде следующей формулы:

NPV = PV — PIV = ∑ _t=1,2,…,n CF_t / (1 + d)^t — ∑ _t=1,2,…,n I_t / (1 + d)^t,

где через I_t обозначен объем инвестиционных средств, которые предполагается вложить в проект за период t.

Таким образом, если NPV > 0, то проект окупается и, как минимум, его можно рассматривать.

На практике ставка дисконтирования может «плавать» год от года. Например, ЦБ может для макроэкономики страны устанавливать
стратегическую цель, в соответствии с которой предполагается «борьба с инфляцией» и которая буквально формулируется так:
«в течение следующих пяти лет мы планируем добиться снижения инфляции с нынешних 12% до 4% через пять лет, так чтобы в следующем
году инфляция составила 10%, через два года 7% и далее в течение очередных трех лет снижение инфляции происходило ежегодно на один
процентный пункт до целевого уровня в размере 4%». Стратегия? Да, конечно, стратегия и вполне себе определенная…

В таком случае, обладая, так сказать, сегодня таким знанием странно было бы не учитывать его (знание о стратегии государства)
для планирования инвестиционных проектов будущего.

Тогда формула расчета NPV будет иметь следующий вид:

NPV = ∑ _t=1,2,…,n CF_t / D_t — ∑ _t=1,2,…,n I_t / D_t,

где для каждого t=1,2,…,n через D_t обозначается произведение

D_t = (1 + d₁) * (1 + d₂) * … * (1 + d_t),

где в свою очередь d_i — ставка дисконтирования i-того периода.

Приведем пару примеров. Пусть «на руках» имеются 10 млн. руб., которые их владелец планирует сохранить для своего однолетнего
ребенка для его обучения (поступления, оплаты обучения, проживания и т.п.) в ВУЗе через 15 лет. Допустим в первом случае он (владелец)
кладет эти деньги в банк под 9% годовых, а во втором случае – покупает квартиру в Москве для сдачи ее в аренду, денежные средства от
которой он также кладет в банк под 9% годовых, постепенно накапливая депозит. Также будем предполагать, что согласно условиям
депозитного договора и в том и другом случае период капитализации депозита составляет один год, причем во втором случае владелец
собирает в течение года денежные средства, поступающие от сдачи в аренду квартиры и потом общую сумму кладет на депозит в начале очередного года.

Для начала будем считать, что финансовые условия в течение 15 лет не меняются и общая официальная инфляция составляет 10%.

Тогда в первом случае на конец 15-ого года владелец 10 млн. руб. в номинале получит сумму из банка в размере:

10млн.руб. * (1 + 9%)¹⁵ = 36,4млн.руб.

Если в качестве коэффициента дисконтирования рассмотреть инфляцию в размере 10% и привести к начальному моменту,
полученные через 15 лет 36,4 миллиона, то получим:

36,4млн.руб. / (1 + 10%)¹⁵ = 8,7млн.руб.

То есть с точки зрения покупательной способности денежных средств потери составят разницу между 10-тью изначальными миллионами
рублей и приведенными к начальному моменту 8,7 млн.руб., равную 1,3млн.руб.

Теперь возвращаемся к сформулированной выше цели вложения денежных средств на 15 лет – сохранение денег для обучения ребенка в ВУЗе.
Это значит, что такое вложение является целевым, под покупку конкретного продукта (образовательных услуг) через 15 лет, и поэтому не
совсем корректным является применение общего показателя инфляции в качестве ставки дисконтирования.
Следовательно необходимо, как минимум, изучить и спрогнозировать средний уровень инфляции в сфере предоставления услуг обучения ВУЗами,
и если он окажется ниже 9% (ставки банковского депозита), то вложение очевидно является состоятельным по отношению к выбранной цели.

Причем имеет смысл рассмотреть в том числе и вариант, когда инфляция услуг обучения, которая в нашем случае берется за
коэффициент дисконтирования, ниже годовой ставки банковского депозита. В этом случае родитель ребенка получает доход, что немаловажно.
Если, например, стоимость услуг обучения в ВУЗе растет год от года в среднем на 7%, то «родитель-инвестор» может рассчитывать на доход,
размер которого с точки зрения его приведенной стоимости составит:

(36,4млн.руб. — 10млн.руб. * (1 + 7%)¹⁵) / (1 + 10%)¹⁵ =

= (36,4млн.руб. – 27,6млн.руб.) / (1 + 10%)¹⁵ =

= 8,8млн.руб. / (1 + 10%)¹⁵ = 2,1млн.руб.

Здесь мы естественно для дисконтирования применяем общий показатель инфляции (10%), поскольку не знаем на что родитель-инвестор
собирается потратить свой дополнительный доход. Заметим, что воспользоваться рассчитанной приведенной суммой в размере 2,1 миллиона
в полном объеме наш заботливый инвестор сможет только через 15 лет – как видно из расчетов, тогда это уже будет сумма в номинале
в размере 8,8 млн.руб.

Если же наш владелец начального капитала пожелает каждый год выводить свой дополнительный доход при начислении процентов и
не оставлять далее на депозите эти 2%, например, будет тратить на свою текущую жизнь, то в таком случае его приведенный к
начальному моменту времени дополнительный доход составит 2,3 млн.руб. – предлагаем читателю самому произвести необходимые расчеты,
чтобы убедиться в этом. То есть получается, что при таком подходе родитель получит больший доход (с точки зрения стоимости денег)
и при этом еще и сможет им воспользоваться в течение 15-ти лет, а не после их прошествия, что на первый взгляд кажется странным и
логически неверным, но именно расчеты показывают верность такого заключения.

Теперь обратимся ко второму из рассмотренных вариантов сохранения денежных средств – к инвестпроекту вложения капитала в квартиру
с целью ее сдачи в аренду. Допустим за 10 млн. руб. покупается «двушка» в Москве в районе, где ее можно сдавать ежемесячно за 50 тыс. руб.,
и денежные средства, получаемые в качестве оплаты услуг аренды, накапливаются в течение года и кладутся на депозит со ставкой 9%
и с такими же прочими условиями по депозиту, как и выше.

При условии, что купленная квартира будет продана через 15-ть лет, получаем следующую формулу для номинального дохода
нашего второго «инвестпроекта»:

I * (1+i₁)ⁿ + R_Y * ∑ _{t=0,1,…,n-1} (1+i₂)^t * (1+r)^n-t-1.

В этой формуле через I обозначен объем начальных инвестиций, равный 10 млн.руб., через i₁ и i₂обозначены
прогнозные уровни инфляции для стоимости квартир и стоимости услуг аренды соответственно в рассматриваемом регионе,
через R_Y обозначен годовой доход от сдачи квартиры, в нашем случае он равен 600 тысяч рублей (50т.р./мес. умножить на 12 месяцев),
наконец, через r обозначена годовая ставка по депозиту, равная в нашем случае 9%, и n – период инвестиционного проекта в количестве лет,
составляющий 15 лет согласно наших предпосылок.

Теперь если предположить, что в среднем ежегодный прирост стоимости купленной квартиры составит i₁=3%,
и уровень прироста ставки ее аренды также будет i₂=3%, то не сложно посчитать по приведенной формуле,
что в конце 15-ого года объем денег на руках инвестора составит ровно те же 36,4 млн. руб. – столько же сколько при вложении начальных
10-ти миллионов на депозит под 9% годовых, см. расчет выше.

Встроив, например, в EXCEL-файл все приведенные здесь формулы можно получить удобный финансовый калькулятор,
с помощью которого легко будут просчитываться и сравниваться между собою результаты возможных вариантов вложений
денежных средств и пользователь сможет принимать соответствующие решения.

Итак, уже на этом этапе рассмотрения основ NPV-анализа понятно, что вопрос об уровне ставки дисконтирования не такой уж и тривиальный.

В отношении ставки дисконтирования важно то, чтобы «потребности инвестора совпадали с его возможностями», поскольку ставку дисконтирования
еще определяют, как уровень средней ежегодной доходности альтернативного инвестиционного проекта или альтернативного вложения капитала.
Инвестор конечно же может для себя определять/рассчитывать ставку дисконтирования по какой-либо из известных классических формул,
общая суть которых сводится к следующей (формуле):

d = i + r + σ.

Которая «читается» так: ставка дисконтирования равна уровню инфляции i плюс «желаемый» уровень чистой (с учетом инфляции)
доходности вложенного капитала r плюс премия за риск σ. И, если опять же обыденно смотреть на эти вещи, то означает это
примерно то, что инвестор не желает потерять покупательную способность инвестированных денежных средств в связи с инфляцией i,
т.е. необходимо сохранить капитал, и при этом желает получить чистый, очищенный от инфляции доход r, другими словами,
успешная реализация инвестиционного проекта должна привести к приросту капитала с точки зрения его реальной рыночной ликвидности,
ну и третье слагаемое σ в этой формуле означает, что инвестор не прочь получить еще и «небольшой» бонус или сверхдоход за то,
что «отважился на вход» в проект с определенной долей риска, который оценивается в размере σ.

Вполне себе нормальное желание, если не брать в расчет того факта, что с такой «желаемой» доходностью у инвесторов чаще
всего нет альтернативных инвестпроектов, поэтому в результате ставку дисконтирования просто-напросто приводят к уровню ставки
банковского депозита, усредненной по, например, первой десятке банков и от этого отталкиваются.

Если рассмотреть чистый дисконтированный доход проекта, как функцию от ставки дисконтирования NPV(d)и решить уравнение

NPV(d) = 0,

т.е. найти такой уровень ставки дисконтирования d, при котором приведенный финансовый поток проекта сравняется с приведенными
инвестиционными вложениями в него. То мы получим крайне важный показатель, характеризующий эффективность инвестиционного проекта,
а именно внутреннюю норму доходностиинвестпроекта, обозначаемую через IRR — Internal Rate of Return, и, как мы уже сказали выше,
получаемую из уравнения:

NPV(IRR) = 0.

В общем случае данное уравнение согласно хорошо известной теореме Абеля из курса алгебры, которая говорит о том,
что уравнения, начиная с пятой степени, не имеют представления корней в радикалах, нельзя решить так, чтобы прописать
единую формулу, например, для расчета IRR в EXCEL в рамках финансовой модели инвестиционного проекта. Поэтому обычно
используется итерационный метод дихотомии нахождения приближенного значения внутренней нормы доходности IRR проекта с наперед заданной точностью.

Например, в приведенной нами в начале этой страницы финансовой модели инвестиционного проекта в EXCEL внутренняя норма
доходности IRR инвестпроекта рассчитывается во вкладке «NPV» в строках с 61ой по 160тую путем применения метода дихотомии с
50-тью итерациями.

Суть метода дихотомии нахождения внутренней нормы доходности IRR состоит в том, чтобы заключить ставку IRR между двумя
такими аргументами d₀ и d₁, что выполняются одновременно два неравенства:

NPV(d₀) > 0 и NPV(d₁) < 0.

После чего отрезок (d₀,d₁) делится пополам – обозначим соответствующий аргумент через d₂,
и в случае если NPV(d₂)>0, то в качестве отрезка (d₀,d₁) при следующей итерации рассматривается
отрезок (d₂,d₁) или если NPV(d₂)<0, то в качестве отрезка (d₀,d₁)
при следующей итерации рассматривается отрезок (d₀,d₂). И так далее, проведя достаточное количество
подобных итераций, мы можем получить приближение к значению внутренней нормы доходности IRR с любой наперед заданной точностью.

В случае если внутренняя норма доходности IRR инвестиционного проекта оказалась выше рассматриваемой инвестором,
«комфортной» для него ставки дисконтирования d_I, т.е.

IRR > d_I,

то считается, что проект имеет смысл рассматривать.

Или если анализируются одновременно несколько возможностей инвестирования в различные проекты, то при прочих равных возможностях
предпочтение отдается тому инвестпроекту, у которого внутренняя норма доходности выше или, что тоже самое, тому проекту,
который выдерживает больший уровень дисконтирования.

В приведенных выше двух примерах при вложении 10-ти миллионов рублей родителем-инвестором предполагалось,
что в конце периода инвестирования денежные средства в полном объеме выводились «на руки» либо с банковского депозита,
либо при продаже квартиры через 15 лет, так сказать, инвестиционный проект имел некое завершение для инвестора.
Но, вообще говоря, можно рассматривать вложения в инвестиционные проекты, при которых не предполагается окончания действия проекта,
т.е. проект можно рассматривать, как бесконечно действующий с точки зрения жизни инвестора и в том числе его наследников,
что означает предположение о том, что активы в которые вложены инвестиционные денежные средства или соответствующий капитал
будут неограниченно долго генерировать постоянный, например, ежегодный доход.

В случае с банковским депозитом этот доход будет ежегодно составлять 900 тыс. руб., при условии что не происходит капитализации
по депозиту, если, например, вкладчик выводит проценты на текущие нужды. В случае со сдачей квартиры в аренду ежегодный доход составит
600 тыс. руб., умноженные на инфляционный коэффициент, в нашем случае это 1+i₂, где i₂ –
инфляция арендных ставок на рынке сдачи жилья в рассматриваемом регионе.

Мы же рассмотрим в этой связи вложения в акции на фондовом рынке с целью систематического получения дивидендов,
т.е. без цели их перепродажи по более высокой цене. Пусть дивиденды по купленным акциям какого-либо эмитента составляют p рублей,
пусть также ежегодно прогнозируется увеличение объема дивидендов по данному эмитенту на i процентов, тогда приведенный финансовый
поток при таком инвестиционном вложении будет иметь следующий вид:

∑ _{t=0,1,…,∞} p * ( 1 + i )^t / ( 1 + d )^t,

где, как обычно, d – ставка дисконтирования.

Соответственно мы получаем бесконечную сумму геометрической прогрессии со знаменателем

q = ( 1 + i ) / ( 1 + d ).

Из математики хорошо известно, что такая сумма имеет конечное значение, если знаменатель qположителен и меньше единицы,
т.е. в нашем случае если ставка дисконтирования d больше ожидаемого среднегодового прироста размера дивидендов i.

Предположим, что именно так и есть в рассматриваемом нами случае: 0 < q < 1 или i < d.

Посчитаем чему равна указанная сумма или чему равен в этом примере приведенный финансовый поток неограниченных
по сроку дивидендных выплат. Для этого сначала посчитаем чему равна сумма первых n+1членов геометрической прогрессии

S_n = ∑ _t=0,1,…,n p * q^t.

Имеет место система двух уравнений:

S_n+1 — S_n = p * qⁿ⁺¹,

q * S_n — S_n+1 = -p.

Из первого уравнения получаем

S_n+1 = S_n + p * qⁿ⁺¹.

Подставляем полученное выражение для S_n+1 во второе уравнение и получаем искомую сумму первых n+1членов нашей геометрической прогрессии:

S_n = p * ( qⁿ⁺¹ — 1 ) / ( q – 1 )

или, как чаще она (формула) выглядит:

S_n = p * ( 1 — qⁿ⁺¹ ) / ( 1 — q ).

Теперь устремляя n в бесконечность получаем приведенный финансовый поток PV дивидендных выплат по акциям нашего эмитента:

PV = p / ( 1 — q ),

куда вместо q подставляем выражение ( 1 + i ) / ( 1 + d ) и имеем окончательную формулу приведенного финансового потока для нашего примера:

PV = p * ( 1+ d ) / ( d — i ).

В заключение предположим, что родитель-инвестор из нашего второго примера не собирается продавать через 15-ть лет квартиру,
купленную за 10-ть миллионов, да и вообще никогда не собирается продавать, а просто планирует получать арендные платежи с
квартиросъемщиков и тратить их на текущую жизнь, т.е. по аналогии с вложениями в акции в качестве дивидендного дохода p он
имеет 600 тысяч рублей. Тогда если общая инфляция d, как было рассмотрено выше и которая считалась в качестве ставки дисконтирования,
составляет 10%, а инфляция по арендным платежам i предполагается равной 3%, то наш родитель получит от вложения в квартиру сумму равную

PV = p * ( 1+ d ) / ( d — i ) = 600 тыс. руб. * ( 1 + 10% ) / ( 10% — 3% ) = 9 429 тыс. руб.

То есть прогнозный приведенный доход будет вполне себе сравним с изначально вложенными 10-тью миллионами рублей.

Аналогично каждому инвестору приходится рано или поздно принимать решение о том, чтобы остаться в инвестпроекте и
получать бессрочный, рассчитываемый по подобным формулам, приведенный дисконтированный доход на вложенный инвестиционный капитал,
или выйти из него взяв свою долю здесь и сейчас по текущей рыночной цене.

Вообще говоря, финансовая и инвестиционная математика – дело заманчивое и интересное. Но, как мы видим из примеров этого раздела,
помимо всего прочего еще и важное. Приведем еще один простой пример наглядно иллюстрирующий место высшей математики
в сфере принятия инвестиционных решений.

Как обычно, сформулируем начальные предпосылки для очередного нашего примера.
Допустим Вы решили сажать картошку в Подмосковье, собирать урожай и потом его продавать.
Для этого Вам предположим необходимо купить лопату и землю, т.е. произвести инвестиционные вложения
во внеоборотные активы для производства картофеля.

Пусть также при выборе лопаты Вам предлагают два экземпляра за одну и ту же цену, отличающиеся между собой только длиной черенка.
Тогда естественно Вы выбрать должны более длинный экземпляр при прочих равных условиях.
Как в этом случае принять решение без прибегания к математическим расчетам?
Очевидно, необходимо приложить обе лопаты к общему началу отсчета кончиками черенков и визуально сравнить их длины,
и соответственно принять решение о покупке той лопаты, которая оказалась на Ваш взгляд в буквальном смысле длиннее.
Итак, одно инвестиционное решение принято.

Теперь предположим, что Вам за одну и ту же цену предлагают два участка земли, один из которых на юге Подмосковья,
а другой – на севере. Понятно, что в этом случае приложить их друг к другу, чтобы увидеть какой больше, а какой меньше, не получится,
да и предположим еще, что «на глаз с вертолета» их тоже невозможно оценить, поскольку их границы не квадратные или прямоугольные, а какие-то
разнообразно кривые. Естественно для принятия решения без математики здесь уже не обойтись – для принятия решения о покупке,
о втором принципиальном инвестиционном вложении средств, Вам необходимо рассчитать площадь каждого участка,
т.е. поставить в соответствие каждому объекту вложения некоторое число, а именно число гектаров земли, после чего сравнить эти
два числа на предмет больше-меньше.

Если Вы сами не владеете методами расчета площади земли, то Вам придется нанять специального оценщика,
который рассчитает площади каждого из участков. Отметим здесь, что за расчет площадей в математике отвечают интегралы,
ну а на практике, например, метод триангуляции.

Отлично! Оценщик посчитал и «принес Вам на блюдечке» две цифры, Вы заплатили за участок, который имеет бОльшую площадь, и
Ваш проект стартанул.

Здесь-то и возникает главный вопрос: математика-то математикой, а вдруг оценщик ошибся в расчетах или хуже того по каким-либо
причинам оказался недобросовестным и специально произвел расчеты так, что по факту меньший участок земли получил в соответствие
при расчетах оценщика большую площадь, и Вы в результате приняли неверное решение, а это значит, что, как минимум,
Вам придется дольше «отбивать» свои инвестиционные вложения.

Конечно же математика важна, но вопрос доверия при инвестировании не менее важен. Жизнь знает огромное количество самых разных
примеров: и когда инвестиционные расчеты заведомо были неверными, а инвестор принимал решение в пользу таких проектов,
доверяя представившим эти расчеты инвестиционным аналитикам, после чего «вылетал в трубу», и когда расчеты были верными,
а люди представлявшие такие расчеты и желающие запустить свой «супермега» проект были профессионалами своего дела и
кристально честными, но инвестор отказывался от вложений, поскольку по причинам известным только ему самому он не доверял
этим людям и, тем самым, упускал прекрасную возможность хорошо заработать.

Никакая премия за риск в рамках расчетов ставки дисконтирования не защитит Вас от лопнувшего недобросовестного банка,
в который Вы положите деньги в сумме, большей, чем максимальный размер застрахованного вклада по системе страхования вкладов,
или от сгоревшей квартиры, которую Вы сдадите недобросовестному квартиросъемщику, или от недобросовестных топ-менеджеров инвестиционного
проекта, куда Вы вложили Ваши кровные, откуда, упомянутые топ-менеджеры выведут в оффшоры оборотные средства предприятия,
а точнее просто своруют их.

Вопросы доверия находятся в области, так называемых, неявных факторов, изучением нивелирования негативного влияния которых
занимается теория управления рисками. И если кратко, то основной вывод этой теории состоит в том, что главным спасением от этих
самых неявных факторов или главным спасением от реализации рисков негативного воздействия является выстраивание такой системы
принятия решений, при которой своевременно принимаются компетентные и правильные решения, короче говоря, необходимо «держать нос по ветру»,
а «ухо востро».

Данная тема, равно как управление рисками, так и формирование эффективной системы принятия решений, будет рассмотрена нами подробно
в других одноименных разделах сайта, а сейчас мы переходим к изложению методологии финансового моделирования инвестиционного
проекта или просто – методологии инвестиционного моделирования, на примере финмодели, EXCEL-файл с которой был выложен для
скачивания в начале настоящей статьи и который можно также
скачать здесь.

Легенда инвестиционного проекта, моделирование которого представлено в EXCEL-файле, заключается в следующем.
Инвестиционные средства вкладываются в создание производства некоторых товаров, в проекте они названы готовой продукцией,
прибыль от продажи которых направляется на погашение задолженности производственного предприятия перед инвесторами.
Срок инвестирования рассматривается в размере 10-ти лет, расчеты финмодели производятся в ежемесячной динамике, начало периода
пользователь может задавать сам из выпадающего списка первых чисел различных годов.

С точки зрения специфики объектов капитальных затрат финмодель различает только то, что на инвестиционные средства
приобретается производственная инфраструктура, без уточнения способа приобретения – будь то строительство с нуля или покупка
готовых производственных мощностей (зданий, сооружений, оборудования и т.п.), включающая в себя склад сырья и материалов и
склад готовой продукции, а также площади для персонала, в том числе офисные для управленческого персонала,
т.е. аренды офисов не предполагается, также как не предполагается капитальных вложений в торговую и логистическую
инфраструктуру – нет своих магазинов и транспортных средств – логистика на аутсорсинге.

Финмодель позволяет задавать уровень максимальной выработки готовой продукции в месяц, при этом план продаж в количестве
готовой продукции задается независимо от максимальной выработки производства. Поэтому в инвестиционной модели предусмотрена
возможность расширения или масштабирования производства путем капитальных вложений в дополнительные производственные модули,
подобные изначальному, источником финансирования которых также являются инвестиции.
То есть предполагается, что если в какой-либо будущий период для выполнения плана продаж необходимо производство продукции
в объеме превосходящем максимальную выработку одного производственного модуля, то финмодель автоматически рассчитывает
инвестиционные капитальные затраты на создание дополнительных производственных мощностей, тем самым, формируется инвестиционный поток модели.

EXCEL-файл с инвестиционной моделью состоит из 10-ти вкладок, в первой из которых, во вкладке «оглавление» представлен список с
указанием содержания оставшихся 9-ти вкладок и гиперссылками на них (в файле финмодели предусмотрена возможность перемещения между
вкладками посредством гиперссылок через оглавление), кратко это выглядит так:

В листе «условия» пользователь финмодели задает основные исходные условия для моделирования инвестиционного проекта.
Начинается все с задания даты старта проекта в ячейке M11 из выпадающего списка дат (набор дат этого списка можно поменять во вкладке «структура»,
в столбце D). После чего в строках 7, 8 и 9 происходит автоматическая разбивка инвестиционного периода на 10-ть последующих лет.

В строке 13 «условий» задаются общие ежегодные объемы капитальных затрат в тысячах рублей на инфраструктуру одного
производственного модуля, с которого проект начинает операционное функционирование.

В строках с 15-той по 48-ую производится ежемесячная разбивка общих сумм капитальных затрат из 13-той строки.
Здесь предусмотрены следующие три способа разбивки, выбор которых осуществляется через выпадающий список ячейки M11
со следующими значениями (названия которых можно поменять во вкладке «структура» в столбце G):

— равномерно по году;

— равномерно с…по…;

— вручную.

При выборе способа «равномерно по году» в строках с 35-той по 46-ую общие суммы из 13-той строки просто делятся на 12
для каждого месяца соответствующего года. При выборе способа «равномерно с…по…» в строках 17 и 18 необходимо выбрать
из списка номера месяцев начала и окончания капитальных вложений данного года, после чего финмодель автоматически распределит
равномерно по выбранным месяцам общие объемы капитальных вложений в блоке строк с 35-ой по 46-ую. Наконец при выборе способа «вручную»
Вам будет предложено в строках с 21-ой по 32-ую просто задать процентное распределение по месяцам года общих сумм капзатрат.

В строке 48 задается номер месяца ввода в эксплуатацию объектов капитальных затрат, причем если этот номер не совпадает
с номером месяца последних ненулевых ежемесячных объемов капзатрат, то ввод в эксплуатацию будет рассчитан в два этапа:
сначала будет введен в эксплуатацию весь объем до указанного месяца, включая его, потом в последний месяц ненулевых объемов
будет введен в эксплуатацию оставшийся объем внеоборотных активов.

В ячейке Q50 задается количество лет амортизации производственных объектов.

В строках с 52-ой по 56-тую задаются ограничения на производственные и складские мощности одного производственного модуля:
максимальный ежемесячный объем выпуска готовой продукции задается в ячейке Q52, объем собственного склада готовой продукции
задается в ячейке Q54, как процент от максимальной ежемесячной выработки, объем собственного склада сырья и материалов – в ячейке Q56
(в удельном пересчете на единицы готовой продукции).

В блоке строк с 58-ой по 77-ую задается план продаж в количестве единиц готовой продукции,
как произведение количества потенциальных клиентов/покупателей в регионе продаж (строка 58), прогнозной целевой доли рынка сбыта,
которую планирует занять предприятие в регионе, (строка 60) и среднее количество единиц продукции, которое будет покупать клиент,
(строка 62).

Операционный цикл нашего предприятия состоит из производственного цикла и торгового цикла, первый из которых
начинается покупкой сырья и материалов и заканчивается выпуском готовой продукции и размещением ее на собственный склад.
Торговый цикл начинается с размещения готовой продукции на склад предприятия и заканчивается ее продажей клиентам.
Соответствующие периоды оборачиваемости или длины указанных циклов задаются в строках 79 и 81.

Такие показатели, как бюджет закупки сырья и материалов, бюджет производства готовой продукции, остатки на конец периода запасов
сырья и материалов, а также готовой продукции, рассчитываются в рассматриваемой финансовой модели с точки зрения классического подхода,
через коэффициенты оборачиваемости, отталкиваясь от бюджета продаж.

Например, для того чтобы рассчитать план производства готовой продукции за период мы используем формулу:

ГП = ГП₁ — ГП₀ + S,

где ГП₁ и ГП₀ – соответственно остатки готовой продукции на конец и начало периода, S – продажи готовой продукции за период.

При этом расчет объема готовой продукции ГП₁ на конец периода производится по такой формуле (можно посмотреть в любом учебнике):

ГП₁ = [ 2 * S * П_об(ГП) / кол-во дней периода ] — ГП₀,

которая вытекает из классического определения коэффициента и периода оборачиваемости запасов готовой продукции, где П_об(ГП) –
заданный в строке 79 вкладки «условия» период оборачиваемости готовой продукции.

Естественно задавая объем запасов ГП₀ для первого периода нашей инвестмодели равным нулю, мы последовательно
применяя вышеприведенные формулы для каждого очередного периода, а в нашем случае это месяцы (см. вкладку «monthly»),
получаем объемы производства за период и остатки запасов ГП на конец периода.

Аналогично рассчитываются объемы закупки сырья и материалов за период, а также запасы на конец периодов сырья и материалов
через заранее рассчитанный план производства готовой продукции и заданный в строке 81 период оборачиваемости запасов сырья и
материалов относительно выпуска готовой продукции.

Заметим лишь то, что формулы с оборачиваемостью запасов и готовой продукции мы применяем в финмодели для продаж выраженных в натуральных
величинах, т.е. в количестве единиц готовой продукции, после чего задавая в строках 83, 85 и 104 соответственно плановую себестоимость
продукции, прогнозную инфляцию в рамках стоимости сырья и материалов, а также наценку при продажах, получаем бюджет закупок,
план производства и остатки запасов сырья и материалов и готовой продукции в деньгах, в нашем случае в тысячах рублей.

Все расчеты инвестиционной модели происходят в ежемесячной детализации во вкладке «monthly», после чего данные поступают в
листы нашего EXCEL-файла с итоговыми формами финансовой управленческой отчетности, см. оглавление выше по тексту.

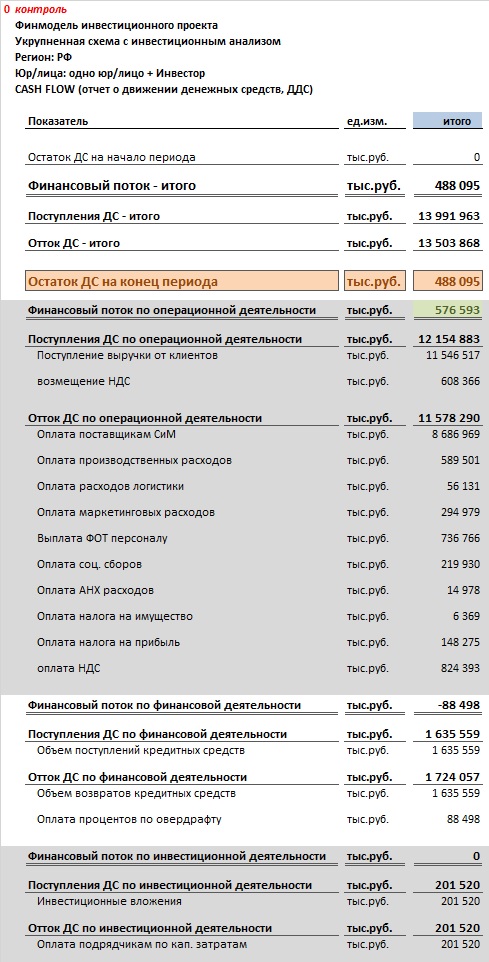
Отчет о прибылях и убытках или как сейчас стало принятым говорить, «отчет о финансовом результате (P&L) в финмодели представлен
в двух вариантах, а именно в виде маржинального P&L и функционального P&L – вкладки «PL_m» и «PL_f».

В маржинальном отчете о прибылях и убытках все расходы разделяются на переменные и постоянные, т.е. на те статьи, которые
зависят от тех или иных доходных показателей и на статьи, прямо не зависящие от них. С шаблоном/форматом маржинального P&L
можно ознакомиться ниже:

В функциональном отчете о прибылях и убытках все расходы разделяются по принципу функциональной принадлежности,
т.е. разделение статей расходов происходит согласно утвержденной оргструктуры предприятия, с шаблоном/форматом функционального P&L
можно ознакомиться ниже:

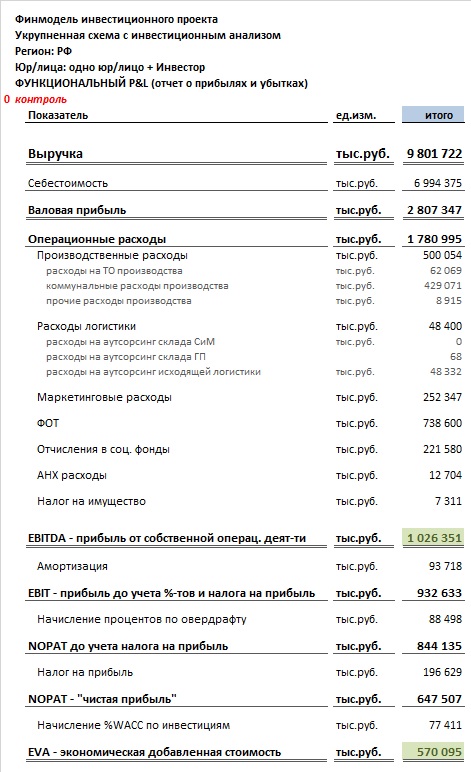
Шаблон/формат отчета о движении денежных средств (Cash Flow), который используется в финмодели выглядит следующим образом:

Формат баланса мы не будем выкладывать, потому как если читателя уже заинтересовала наша финансовая модель инвестиционного проекта,
то наверняка Вы ее скачаете и самостоятельно ознакомитесь с ним (с форматом/шаблоном баланса).

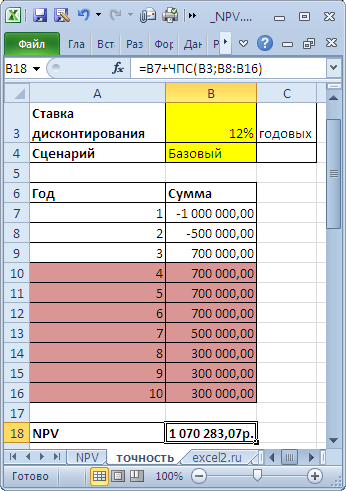
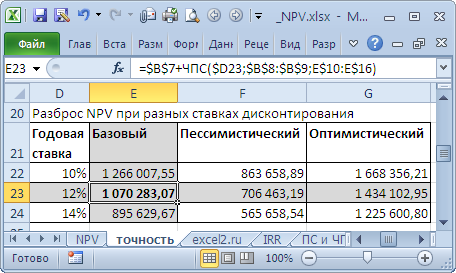
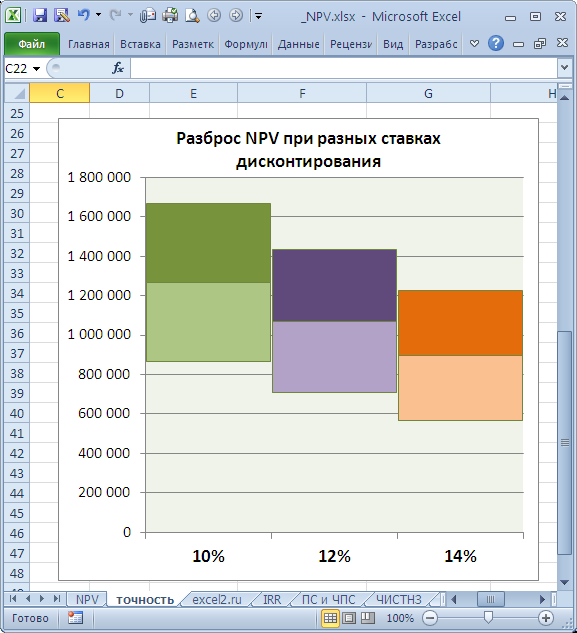
Мы же обратимся к рассмотрению вкладки «NPV», в которой как раз таки с использованием EXCEL-формул проводится NPV-анализ,
где рассчитываются такие показатели, как:

— NPV инвестиционных вложений (Inv);

— NPV потока ДС (CF);

— возврат инвестиций;

— PP — период окупаемости;

— NPV CF после инвестиционного периода;

— PI инвестиционного периода;

— NPV полный;

— PI полный;

— ROI инвестиционного периода;

— ROI полный;

— средняя ставка дисконтирования инвестпроекта;

— IRR — внутренняя норма доходности.

Формат отчета с NPV-анализом инвестпроекта следующий:

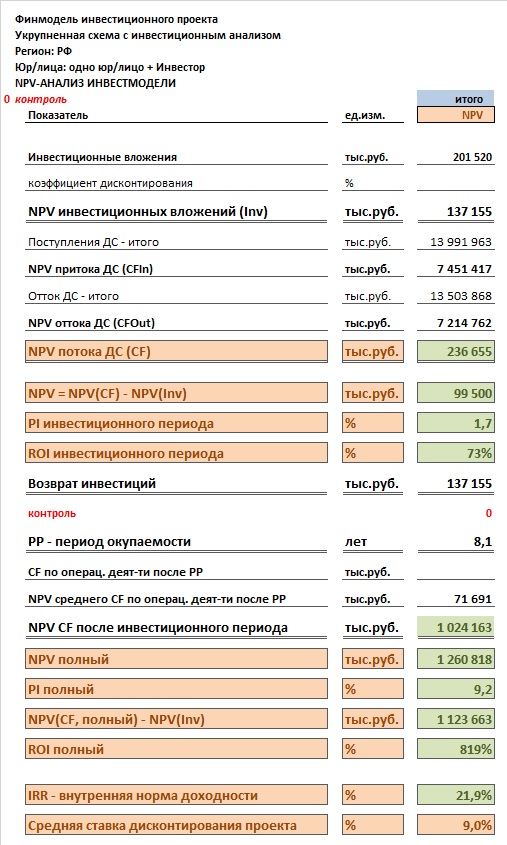
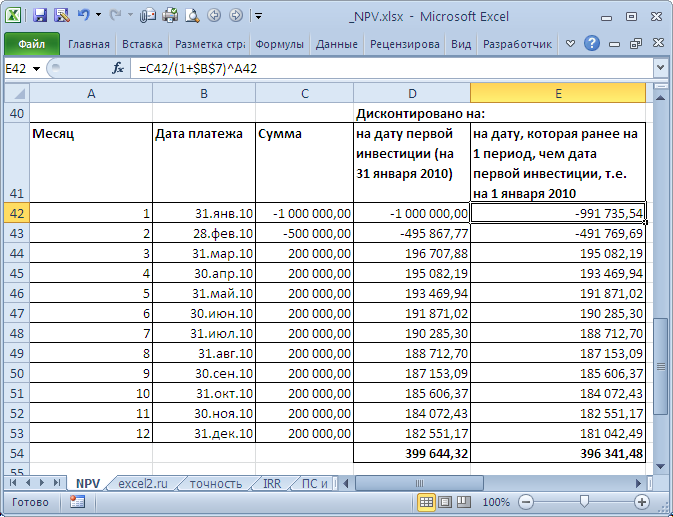
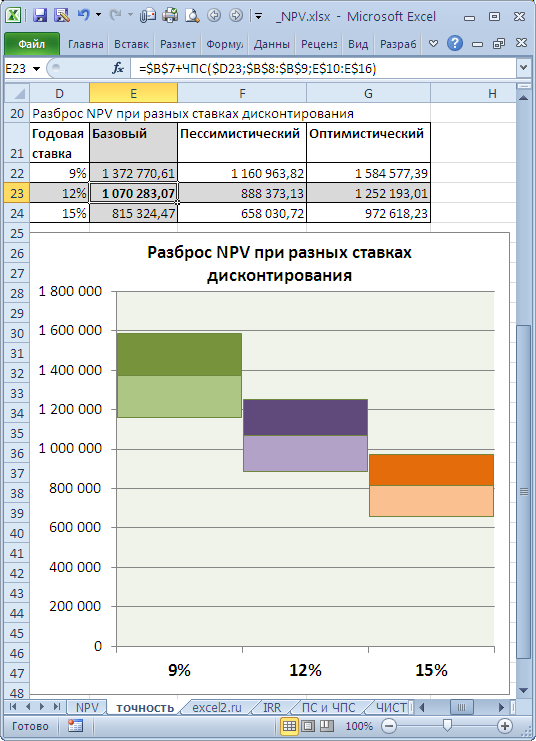
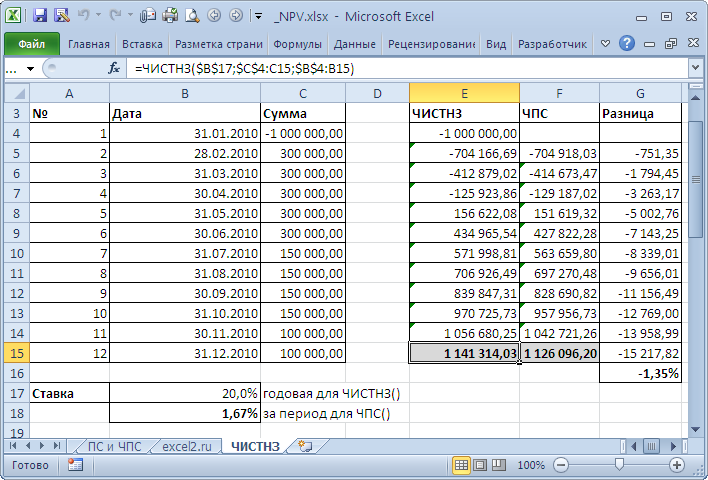
Итак, мы рассматриваем вкладку «NPV». В 12-тую строку этой вкладки мы из отчета Cash Flow вкладки «CF» вносим с помощью
EXCEL-формул данные о потоке инвестиционных вложений в проект на капитальные затраты для создания того количества производственных модулей,
которое необходимо в соответствии с планом продаж готовой продукции.

В строке 14 производится расчет коэффициентов дисконтирования для каждого года на основе данных из строки 188
вкладки «условия», куда пользователь в свою очередь вносит вручную прогнозные ставки дисконтирования финансового потока
отдельно для каждого года инвестпроекта, напоминаем, что эти ставки в общем случае могут быть различными от года к году.

Приведенная стоимость инвестиционных вложений рассчитывается в строке 16 путем суммирования последовательных частных
от деления для каждого года строки 12 с номинальными объемами инвестиций на соответствующие коэффициенты дисконтирования из строки 14.

Далее в строках 20 и 24 рассчитываются аналогичным образом приведенные стоимости притоков и оттоков денежных средств проекта
без учета возврата инвестиционных займов, но с учетом финансовой деятельности предприятия, если топ-менеджменту последнего
пришлось привлекать кредиты на пополнение оборотных средств операционной деятельности.

Рассматриваемая модель предполагает, что инвестиции направляются только на производственную инфраструктуру,
а на поддержание операционной деятельности в случае возникновения кассовых разрывов топ-менеджмент предприятия должен сам
найти возможность привлечения соответствующих кредитов и займов, объемы которых наша финмодель рассчитывает автоматически
через модель овердрафтного кредитования и учитывает эти операции в рамках блока с движением денежных средств по финансовой
деятельности в отчете Cash Flow.

Другими словами, в строке 26 рассчитывается приведенный финансовый поток по основной и финансовой деятельности или, что тоже самое,
финансовый поток по операционной деятельности предприятия, который как раз таки и необходимо сравнить с приведенным потоком инвестиций
из строки 16, что и делается в ячейке M29, в которой считается указанная разница. С помощью условного форматирования EXCEL
ячейка M29закрашивается в зеленый цвет, если значение в ней больше нуля, т.е. проект состоятелен (приведенный финпоток
по операционной деятельности больше приведенного инвестпотока), и окрашивается в красный, если наоборот – проект убыточен
при прочих равных условиях с точки зрения инвестора.

В ячейках M31 и M33 рассчитываются значения показателей PI и ROI:

PI — Profitability Index — Индекс прибыльности инвестиций — равен отношению приведенного финансового потока по операционной
деятельности к приведенной стоимости инвестиционных вложений – очевидно, что должен быть больше единицы, чтобы проект был
предложен к рассмотрению;

ROI — Return On Investment — Рентабельность инвестиций — равен отношению NPV к приведенной стоимости инвестиций.

В строке 35 производится расчет потока возврата инвестиций, в связи с чем в ячейке M39 рассчитывается показатель

PP — Payback Period — Период возврата или окупаемости инвестиций — равен средневзвешенному по суммам возврата количеству лет,
по прошествии которых инвестору вернутся все вложенные в проект денежные средства с учетом заданного уровня дисконтирования.

Далее в блоке строк с 41-ой по 53-тью рассчитываются все уже приведенные ранее показатели эффективности инвестиционного
проекта для случая, если инвестор решит не выходить из проекта, а оставить его для себя «навсегда», см. соответствующие формулы
в первой части этого раздела. Здесь в качестве ежегодного финансового потока на период после 10-ти лет существования проекта
рассматривается средний финансовый поток рассчитанный по периоду следующему после периода окупаемости PP.

Наконец в ячейке M56, а на самом деле в блоке строк с 61-ой по 160-тую путем применения метода дихотомии,
как мы уже отмечали выше, рассчитывается приближенное значение показателя эффективности инвестпроекта IRR —
внутренней нормы доходности. И чтобы его было с чем сравнивать, в случае если от года к году пользователем модели
задаются различные ставки дисконтирования, мы приводим в ячейке M56, с расчетом в блоке строк со 161-ой по 260-тую
среднюю единую для каждого года ставку дисконтирования инвестиционного проекта.

В заключение отметим, что за скобки представленного в настоящей статье материала мы осознанно выносим обсуждение
таких важнейших понятий, как EBITDA и EVA, а также рыночная стоимость чистых активов, философия которых формирует адекватное
понимание того, что такое эффективное управление с точки зрения системы принятия инвестиционных, да и не только, решений.
Также отметим, что взгляд на управление через эти понятия подобен, например, системе управления, называемой «бережливое производство»,
которая сформировалась в Японии. В данном случае речь идет не просто о формулах, через которые формально дается представление
обывателю об этих показателях и связанных с ними понятиях, речь идет о том, как в реальной жизни предприятия внедрить соответствующие
высоко эффективные системы управления, что является базовой отправной точкой для любого инвестора при формировании команды
топ-менеджеров для управления проектом. Указанный материал мы разместим в ближайшем будущем в разделе, посвященном законам
эффективного управления.

Незаполненная инвестиционная модель

СКАЧАТЬ


Незаполненная финмодель инвестиционного проекта, NPV-анализ

Читать далее —
Финмодель инвестпроекта в EXCEL, версия 2.0

В этой статье мы приводим ссылки и описание шести полезных файлов Excel, которые вы можете использовать для принятия инвестиционных решений или получения новых знаний в области инвестиций:

• Построение лестницы облигаций (актуальные обновляемые данные)
• Анализ качества эмитентов облигаций (актуальные обновляемые данные)
• 11 способов расчета доходности инвестиционного портфеля
• Сравнение фондов с выплатами и реинвестированием для цели получения периодического дохода
• Калькулятор процентного риска облигаций
• Шаблон файла для оценки акций

Лестница облигаций

Лестница облигаций — это простая инвестиционная стратегия, позволяющая организовать удобные для инвестора денежные потоки и снизить риск изменения процентных ставок.

Вы определяете число ступеней лестницы (число лет, умноженное на число погашений облигаций каждый год), для каждой ступени находите подходящие для вас облигации и инвестируете в каждую ступень одинаковую сумму денег.

После погашения облигаций в каждой ступени вы выбираете, тратить деньги на свои обычные расходы (или инвестировать в другие альтернативы) и, таким образом, «укорачивать» лестницу или купить новые облигации (на срок в конце лестницы), достроив лестницу до целевого года погашения. Купоны вы можете использовать по своему желанию. Подробно о Лестнице облигаций мы писали здесь.

Этот файл основан на данных нашего сервиса «Анализ облигаций» и обновляется еженедельно. Видео по построению лестницы облигаций и отчету по качеству эмитента смотрите здесь.

Анализ качества эмитентов облигаций

Детальный анализ качества эмитентов облигаций как «со стороны» (долговая нагрузка, эффективность, стабильность), так и «внутри» (анализ качества баланса и качества прибыли). Этот отчет также позволят находить лучшие замены или аналоги для любых облигаций.

Этот файл основан на данных нашего сервиса «Анализ облигаций» и обновляется еженедельно. Для доступа на страницу с файлом может потребоваться очень быстрая регистрация.

11 способов расчета доходности инвестиционного портфеля

Все просто, если в вашем портфеле нет пополнений и выводов денег. Но, как правило, они есть и рассчитывая доходность двумя разными способами, вы можете получить абсолютно разные результаты, вплоть до того, что при одном методе расчета ваша доходность будет положительной, а при другом — отрицательной. И оба эти результата будут являться корректными.

Это файл представляет все 11 способов расчета доходности. Он не универсален для любого портфеля, но с его помощью и нашей подробной статьи вы легко сможете ориентироваться в основных способах расчета и применять их. Решение этой задачки в Telegram также поможет лучше разобраться в использовании различных подходов к расчетам.

Сравнение фондов с выплатами и реинвестированием для цели получения периодического дохода

Если ваша инвестиционная цель — генерация периодического дохода (выплат), вы можете использовать отдельные акции и облигации, а можете фонды. Последние могут выплачивать доходы, а могут их реинвестировать. В случае реинвестирования, вы сможете реализовать свою цель только продавая часть паев на величину ожидаемого дохода.

Этот файл показывает, что такая стратегия более эффективна после учета налогов и временной стоимости денег, чем получение выплат. В решении этого кейса мы объясняем все подробно.

Калькулятор процентного риска облигаций

Облигации с различными характеристиками (срок, доходность, размер, число купонов и пр.) имеют разную чувствительность к изменению рыночных процентных ставок.

Это калькулятор позволяет вычислять процентное изменение цены облигаций в зависимости от изменения процентных ставок (есть формулы и подходы к аппроксимации сложных вычислений типа выпуклости). В конченом итоге, вы можете оценивать процентные риски и потенциальные доходности целых портфелей, как это сделали мы в решении этой задачки в Telegram.

Шаблон файла для оценки акций

Полноценный шаблон оценки акций по модели дисконтированных денежных потоков от профессора Сваминатана, 25 лет преподававшего в Cornell (University of Chicago). Конспекты лекций по оценке и анализу ценных бумаг также отличные.

Бонус: пример боевой оценки акций Tesla от Асвата Дамодарана, профессора финансов в Школе бизнеса Стерна при Нью-Йоркском университете (преподает корпоративные финансы и оценку капитала).

Читайте также:

• 8 лучших книг по анализу отчетности и оценке компаний
• 8 лучших книг для развития знаний об инвестициях
• Три факта об оценке активов
• Законы оценки: Разоблачение мифов и заблуждений
• Роль облигаций в инвестиционном портфеле
• BOND ETF. Первый настоящий фонд облигаций с затратами 0.4%
• и еще десятки полезных публикаций в нашем канале Telregram. Вот тут есть полный гид по каналу

Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.

Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.

Скачать пример

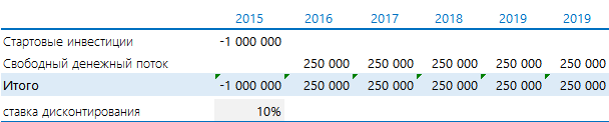
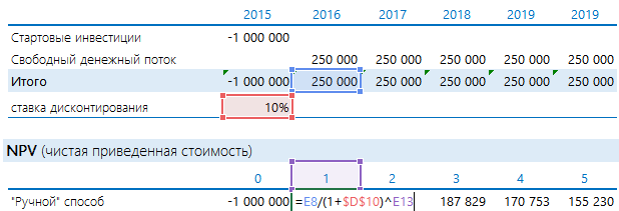
Оценка целесообразности проекта с помощью NPV

Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.

Оцениваем NPV проекта. Напомню формулу этого показателя:

Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:

Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.

Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.

Получается «-52 303». Проект невыгоден.

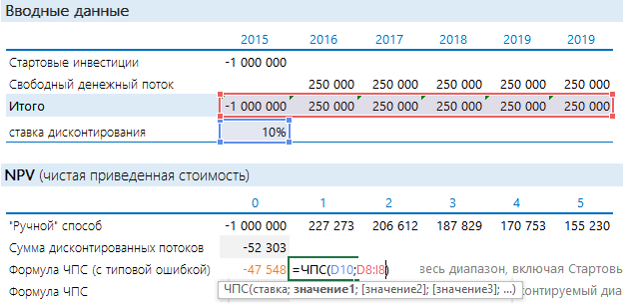
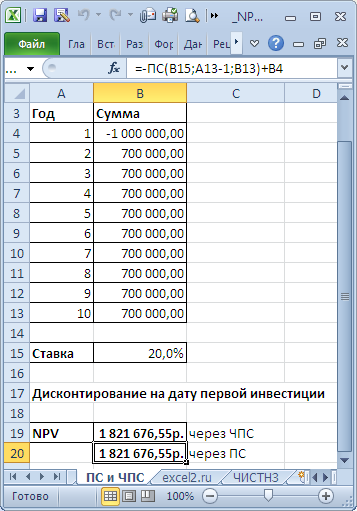
Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):

ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)

То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:

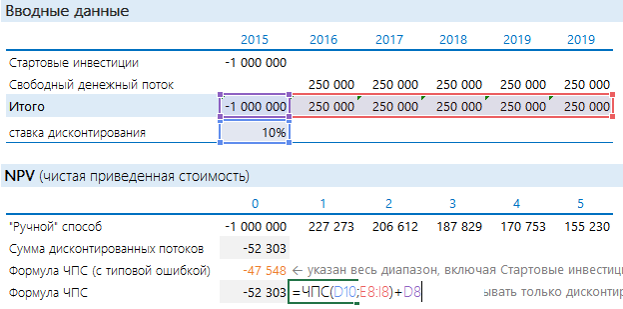
Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:

Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.

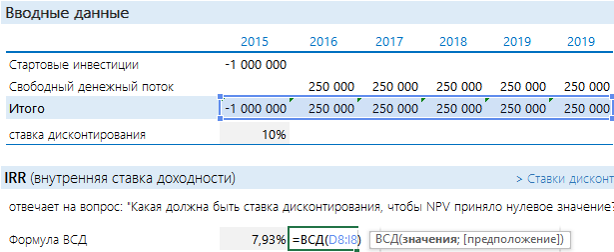
Оценка целесообразности проекта с помощью IRR

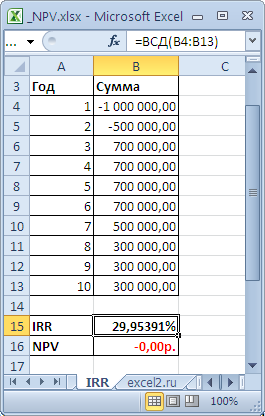
Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования < IRR, то проект стоит принять, если нет – отказаться. Рассчитать IRR с помощью Excel очень просто: подставляем в функцию ВСД итоговый денежный поток.

IRR оказался меньше ставки доходности. Проект невыгодный (тот же вывод, что и при NPV).

NPV и IRR по праву считаются главными экономическими критериями. Их используют и для инвестиционной оценки проектов, и для оценки стоимости существующего бизнеса. В том числе, показатель EVA (Economic Value Added) считается хорошим критерием в том числе потому, что при правильном расчете он равен NPV.

Но кроме всего прочего, NPV и IRR могут быть использованы финансистами в более прикладных вопросах, например, при общении с банками на тему реальной кредитной ставки. Как – давайте посмотрим.

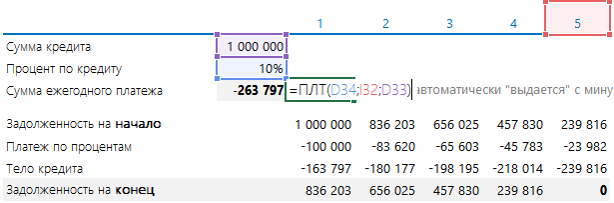
Аннуитеты – любимая банковская цифра

Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:

ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)

В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:

Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.

В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.

Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.

Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:

Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.

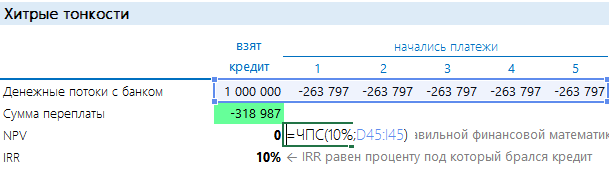
Нюансы и тонкости

А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.

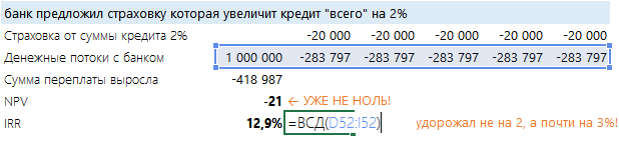
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:

В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…

Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.

Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.

You probably knew that Microsoft’s Excel spreadsheet program is a fine tool for keeping track of your investments in an organized manner, enabling you to see and sort positions, including entry price, periodic closing prices, and returns. But actually, Excel can do much more than serve as a glorified financial statement. It can automatically calculate metrics such as an asset’s or a portfolio’s standard deviation, percentage of return, and overall profit and loss.

Let’s look at how Excel can enhance one’s investment activities.

Tracking Investments With Excel

An Excel spreadsheet can be used in a number of ways to keep track of an investor’s holdings. The first step is to decide what data you would like to include. The figure below shows an example of a simple spreadsheet that tracks one investment’s data, including date, entry, size (how many shares), closing prices for the dates specified, the difference between the closing price and the entry price, the percentage return, profit and loss for each periodic closing price, and the standard deviation. A separate sheet in an Excel workbook can be used for each stock.

Creating Difference Formulas in Excel

Some values in the spreadsheet, however, must be manually calculated, which is time-consuming. However, you can insert a formula into a cell to do the work for you. To calculate the difference of an asset’s current price minus its entry price, for instance, click in the cell where you would like the difference to appear.

Next, type the equals sign (=) and then click in the cell containing the current price. Follow this with a minus sign and then click in the cell that contains the entry price. Then click enter and the difference will appear. If you click on the lower right corner of the cell until you see what looks like a dark plus sign (without little arrows on it), you can drag the formula to the other appropriate cells to find the difference for each dataset.

Creating Percent Return Formulas in Excel

The percent return is the difference of the current price minus the entry price, divided by the entry price: (price-entry) ÷ entry. The percent return calculation is made by, once again, selecting the cell where you would like the value to appear, then typing the equal sign. Next, type an open parenthesis and click in the cell that has the current price, followed by a minus sign, the entry price, and a closing parenthesis.

Next, type a forward slash (to represent division) and then click in the entry price cell again. Press enter and the percent return will appear. You may need to highlight the column, right-click, and select Format Cells to select Percentage under the number tab to make these values appear as percentages. When you have the formula in one cell, you can click and drag (as above) to copy the formula into the corresponding cells.

Creating Profit/Loss Formulas in Excel

The profit and loss formula is the difference multiplied by the number of shares. To create the formula, click in the cell where you want the value to appear. Next, type the equals sign and then click in the cell that contains the difference (see above). Then, type the asterisk symbol (*) to represent multiplication and then click in the cell that contains the number of shares. Press enter and you will see the profit and loss for that data. You may need to highlight the column, right-click, and select Format Cells, then select the currency to set the column to display as a dollar amount. You can then select, click, and drag the formula to copy it into the other corresponding cells.

Creating Standard Deviation Formulas in Excel

The mainstay of modern portfolio theory, the standard deviation for a dataset can reveal important information regarding an investment’s risk. The standard deviation is simply the measure of how far returns are from their statistical average; in other words, it allows investors to determine the above-average risk or volatility of an investment. The standard deviation of returns is a more accurate measure than looking at periodic returns because it takes all values into account.

The standard deviation calculation is a complex, time-consuming mathematical equation. Fortunately, a few simple clicks in Excel can provide the same calculation. Even if an investor does not understand the math behind the value, the risk and volatility of a particular stock or the entire portfolio can be measured with relative ease.

To find the standard deviation of a dataset, click on the cell where you want the standard deviation value to appear. Next, under the Formulas heading in Excel, select the Insert Function option (this looks like fx). The Insert Function box will appear, and under Select a Category choose Statistical. Scroll down and select STDEV, then click OK. Next, highlight the cells for which you want to find the standard deviation (in this case, the cells in the percent return column; be careful to select only the return values and not any headers). Then click OK and the standard deviation calculation will appear in the cell.

Viewing a Portfolio in Excel

You can compile data from the individual sheets in Excel to get a sense of all holdings at a glance. If you have data on one sheet in Excel that you would like to copy to a different sheet, you can select, copy, and paste the data into a new location. In this way, it is easy to import a series of stocks’ data into one sheet. All of the formulas are the same as in the previous examples, and the standard deviation calculation is based on the percent return of all of the stocks, rather than just a single instrument.

The figure below shows data from 11 different stocks, including entry date and price, the number of shares, the current price, the difference between the current price and the entry price, the percent return, the profit and loss, and the overall standard deviation.

Other Tips for Using Excel

When a spreadsheet has been formatted with the data you would like to see as well as the necessary formulas, entering and comparing data is relatively simple. But it pays to take the time to set up the sheets exactly how you want them and eliminate or hide any extraneous data. To hide a column or row of data, highlight it, and under the Home tab, select Format. A drop-down menu will appear; select Hide or Unhide, choosing the option you want. Any data that is hidden can still be accessed for calculations but will not show up in the spreadsheet. This is helpful when creating a streamlined, easy-to-read spreadsheet.

Of course, there are alternatives to setting up the spreadsheet by yourself. A considerable number of commercial products are available from which you can choose portfolio management software that works in concert with Excel. An internet search can help interested investors learn about these opportunities.

The Bottom Line

An Excel spreadsheet can be as easy or complex as you want it to be. Personal preference and needs dictate the complexity of the spreadsheet. The key is to understand whatever data you do decide to include so that you can gain insight from it. Those interested in learning about other ways to use this software may wish to enroll in one of the best online Excel classes currently available.

В статье будет приведен расчет показателей эффективности проекта, с учетом дисконтирования.

• ЧДД или чистый дисконтированный доход от инвестиционного проекта;
• Внутренняя норма доходности.

Рассмотрим эти два показателя подробнее и рассчитаем пример работы с ними в Excel. Еще больше о возможностях Excel можно узнать на нашем открытом курсе «Аналитика в Excel».

Net Present Value (NPV, чистый дисконтированный доход) — один из самых распространенных показателей эффективности инвестиционного проекта.

Это разность между дисконтированными по времени поступлениями от проекта и инвестиционными затратами на него.

Метод расчета NPV:

1. Определяем текущую стоимость затрат (инвестиции в проект)
2. Производим расчет текущей стоимости денежных поступлений от проекта, для этого доходы за каждый отчетный период приводятся к текущей дате

CF – денежный поток;
r – ставка дисконта.

3. Сравниваем текущую стоимость инвестиций (наши затраты) в проект (Io) с текущей стоимостью доходов (PV). Разница между ними будет чистый дисконтированный доход — NPV.

NPV показывает инвестору доход или убыток от вложений средств в проект по сравнению с доходом от хранения денег в банке.

Если NPV больше 0, то инвестиции принесут больше дохода, нежели чем аналогичный вклад в банке.

Формула 1 модифицируется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов).

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
r – ставка дисконтирования;
n – количество периодов.

Internal Rate of Return (Внутренняя норма доходности, IRR) определяет ставку дисконтирования при которой инвестиции равны 0 (NPV=0), или другими словами затраты на проект равны его доходам.

IRR = r, при которой NPV = f(r) = 0, находим из формулы:

CF – денежный поток;
I – сумма инвестиционных вложений в проект в t-ом периоде;
n – количество периодов.

Этот показатель показывает норму доходности или возможные затраты при вложении денежных средств в проект (в процентах).

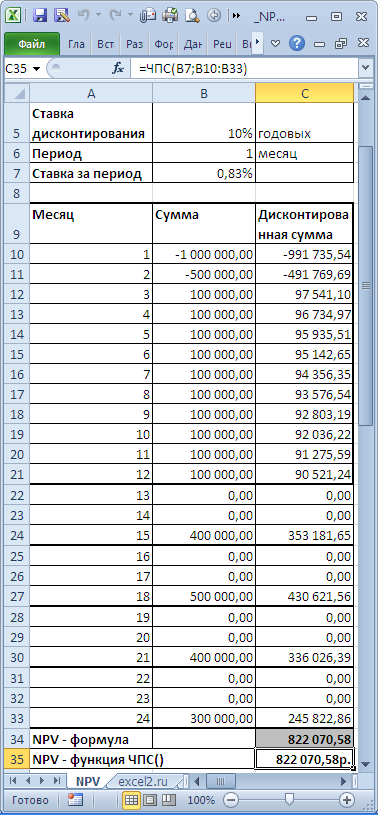
Пример расчета NPV в Excel

В MS Excel 2010 для расчета NPV используется функция =ЧПС().

Найдем чистый дисконтированный доход (NPV) проекта, требующего вложений инвестиций на 90 тыс. руб., и денежный поток которого распределен по времени рис 1. , и ставка дисконта равна 10%.

Рассчитаем показатель NPV по формуле Excel:

=ЧПС(D3;C3;C4:C11)

D3 – ставка дисконта;
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект);
C4:C11 – денежный поток проекта за 8 периодов.

В итоге показатель чистого дисконтированного дохода равен 51,07 >0, это говорит о том, что в проект стоит инвестировать.

Расчет IRR в Excel

Для определения IRR в Excel используется встроенная функция

=ЧИСТВНДОХ()

Но так как у нас в примере данные поступали в равные интервалы времени можно использовать функцию

=ВСД(C3:C11)

Доходность вложения в проект равна 38%.

В завершение картинка финансового анализа проекта целиком.

Каждый человек, который серьезно занимался финансовой деятельностью или профессиональным инвестированием, сталкивался с таким показателем, как чистый дисконтированный доход или NPV. Этот показатель отражает инвестиционную эффективность изучаемого проекта. В программе Excel имеются инструменты, которые помогают рассчитать это значение. Давайте выясним, как их можно использовать на практике.

Расчет чистого дисконтированного дохода

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

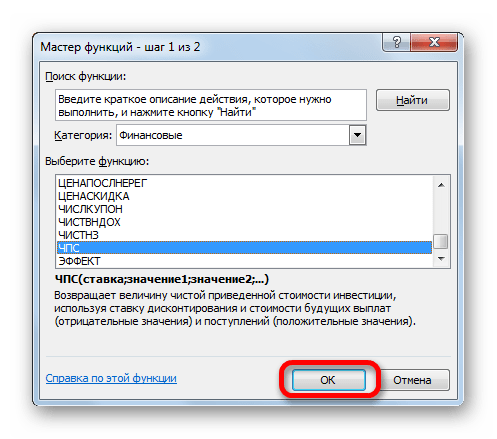
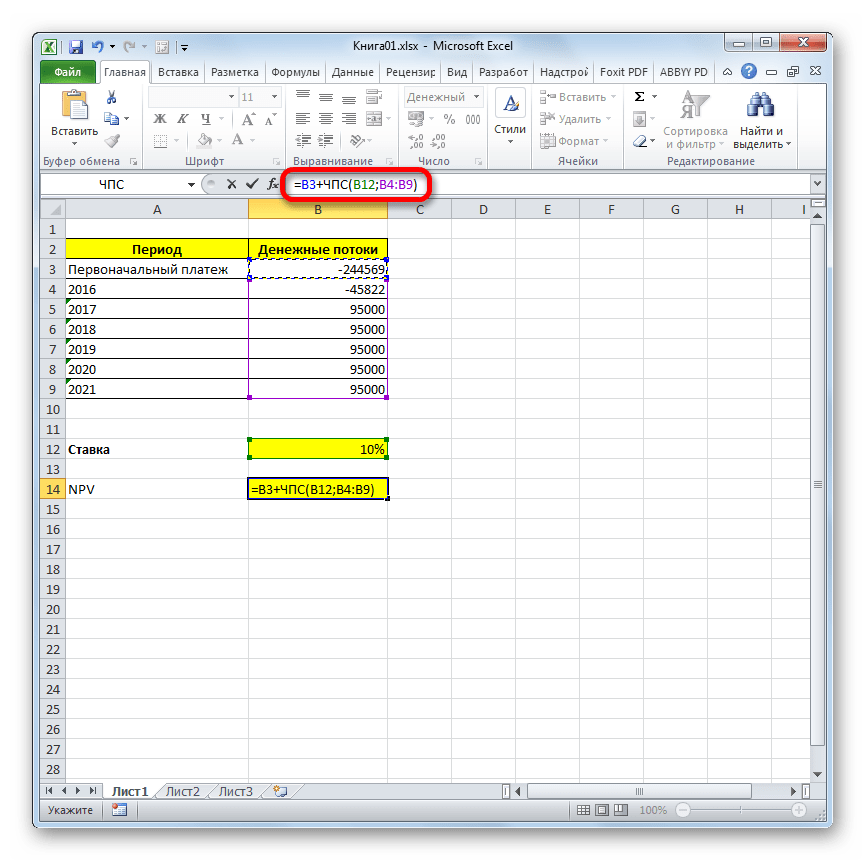
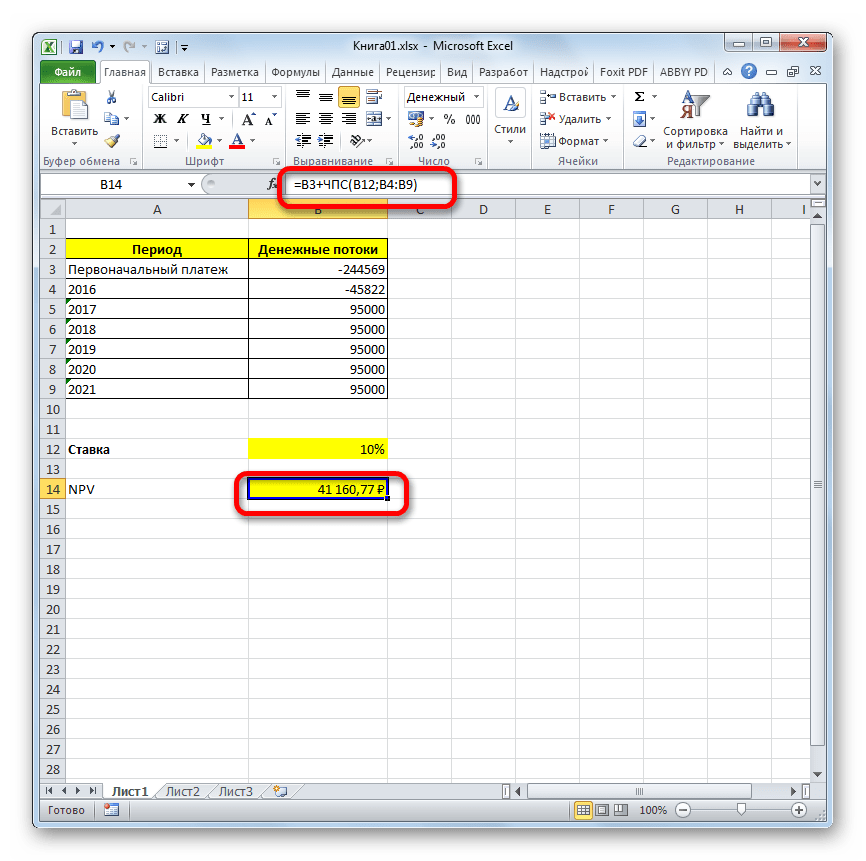
В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:

=ЧПС(ставка;значение1;значение2;…)

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».

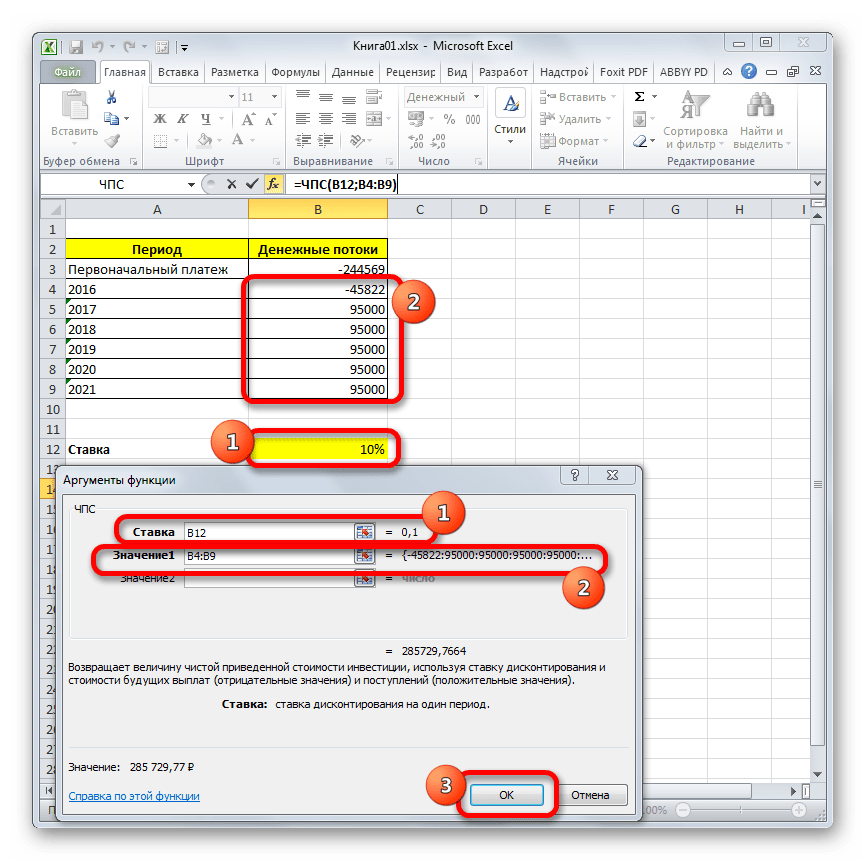
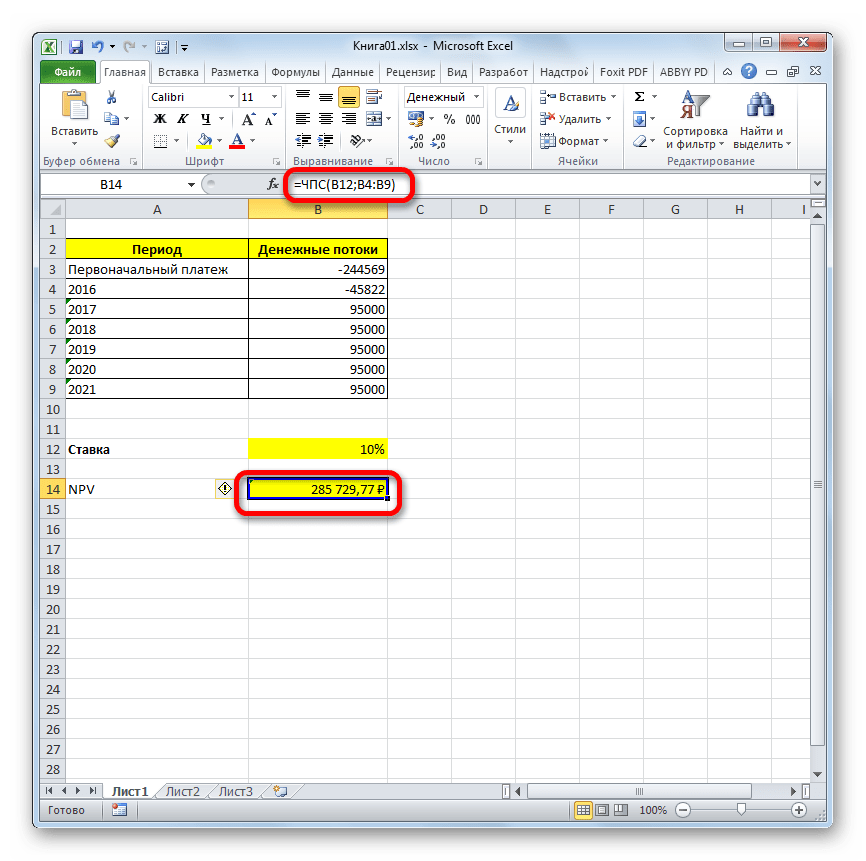
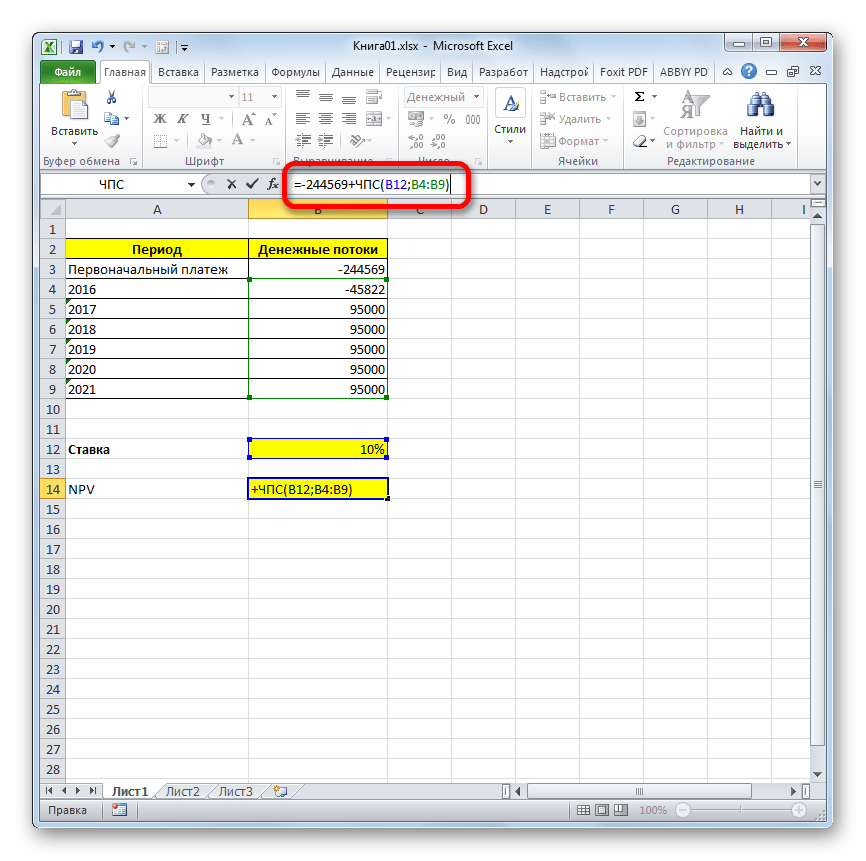
Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

=Первоначальная_инвестиция+ ЧПС(ставка;значение1;значение2;…)

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

1. Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.



2. Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».



3. После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».

   В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

   

   В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

   Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».



4. Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.



5. После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.
   

   Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.



6. Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.

Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Урок: Финансовые функции в Excel

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул

MS

EXCEL.

Начнем с определения, точнее с определений.

Чистой приведённой стоимостью (Net present value, NPV) называют

сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню

(взято из Википедии). Или так:

Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт

cfin.

ru)

Или так:

Текущая

стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика

.

Толковыйсловарь

. —

М

.

:

»

ИНФРА

—

М

«,

Издательство

»

ВесьМир

«.

Дж

.

Блэк

.)

Примечание1

. Чистую приведённую стоимость также часто называют Чистой текущей стоимостью, Чистым дисконтированным доходом (ЧДД). Но, т.к. соответствующая функция MS EXCEL называется

ЧПС()

, то и мы будем придерживаться этой терминологии. Кроме того, термин Чистая Приведённая Стоимость (ЧПС) явно указывает на связь с

Приведенной стоимостью

.

Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма

Приведенных стоимостей

денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.

Совет

: при первом знакомстве с понятием Чистой приведённой стоимости имеет смысл познакомиться с материалами статьи

Приведенная стоимость

.

Это более формализованное определение без ссылок на проекты, инвестиции и ценные бумаги, т.к. этот метод может применяться для оценки денежных потоков любой природы (хотя, действительно, метод NPV часто применяется для оценки эффективности проектов, в том числе для сравнения проектов с различными денежными потоками). Также в определении отсутствует понятие дисконтирование, т.к. процедура дисконтирования – это, по сути, вычисление приведенной стоимости по методу

сложных процентов

.

Как было сказано, в MS EXCEL для вычисления Чистой приведённой стоимости используется функция

ЧПС()

(английский вариант — NPV()). В ее основе используется формула:

CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).

Примечание2

. Т.к. денежный поток может присутствовать не в каждый период, то определение NPV можно уточнить:

Чистая приведённая стоимость — это Приведенная стоимость денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через промежутки времени, кратные определенному периоду (месяц, квартал или год)

. Например, начальные инвестиции были сделаны в 1-м и 2-м квартале (указываются со знаком минус), в 3-м, 4-м и 7-м квартале денежных потоков не было, а в 5-6 и 9-м квартале поступила выручка по проекту (указываются со знаком плюс). Для этого случая NPV считается точно также, как и для регулярных платежей (суммы в 3-м, 4-м и 7-м квартале нужно указать =0).

Если сумма приведенных денежных потоков представляющих собой доходы (те, что со знаком +) больше, чем сумма приведенных денежных потоков представляющих собой инвестиции (расходы, со знаком минус), то NPV >0 (проект/ инвестиция окупается). В противном случае NPV <0 и проект убыточен.

Выбор периода дисконтирования для функции ЧПС()

При выборе периода дисконтирования нужно задать себе вопрос: «Если мы прогнозируем на 5 лет вперед, то можем ли мы предсказать денежные потоки с точностью до месяца/ до квартала/ до года?». На практике, как правило, первые 1-2 года поступления и выплаты можно спрогнозировать более точно, скажем ежемесячно, а в последующие года сроки денежных потоков могут быть определены, скажем, один раз в квартал.

Примечание3

. Естественно, все проекты индивидуальны и никакого единого правила для определения периода существовать не может. Управляющий проекта должен определить наиболее вероятные даты поступления сумм исходя из действующих реалий.

Определившись со сроками денежных потоков, для функции

ЧПС()

нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы  ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см.

файл примера, лист NPV

).

В таблице NPV подсчитан двумя способами: через функцию

ЧПС()

и формулами (вычисление приведенной стоимости каждой суммы). Из таблицы видно, что уже первая сумма (инвестиция) дисконтирована (-1 000 000 превратился в -991 735,54). Предположим, что первая сумма (-1 000 000) была перечислена 31.01.2010г., значит ее приведенная стоимость (-991 735,54=-1 000 000/(1+10%/12)) рассчитана на 31.12.2009г. (без особой потери точности можно считать, что на 01.01.2010г.) Это означает, что все суммы приведены не на дату перечисления первой суммы, а на более ранний срок – на начало первого месяца (периода). Таким образом, в формуле предполагается, что первая и все последующие суммы выплачиваются в конце периода. Если требуется, чтобы все суммы были приведены на дату первой инвестиции, то ее не нужно включать в аргументы функции

ЧПС()

, а нужно просто прибавить к получившемуся результату (см.

файл примера

). Сравнение 2-х вариантов дисконтирования приведено в

файле примера

, лист NPV:

О точности расчета ставки дисконтирования

Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см.

файл примера, лист Точность

).

Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.

NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):

Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.

Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.

Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0

Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.

Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.

После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.

Внутренняя ставка доходности

IRR

(ВСД)

Внутренняя ставка доходности (англ.

internal rate of return

, IRR (ВСД)) — это ставка дисконтирования, при которой Чистая приведённая стоимость (NPV) равна 0. Также используется термин Внутренняя норма доходности (ВНД) (см.

файл примера, лист IRR

).

Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.

Для расчета IRR используется функция

ВСД()

(английский вариант – IRR()). Эта функция тесно связана с функцией

ЧПС()

. Для одних и тех же денежных потоков (B5:B14) Ставка доходности, вычисляемая функцией

ВСД()

, всегда приводит к нулевой Чистой приведённой стоимости. Взаимосвязь функций отражена в следующей формуле:

=ЧПС(ВСД(B5:B14);B5:B14)

Примечание4

. IRR можно рассчитать и без функции

ВСД()

: достаточно иметь функцию

ЧПС()

. Для этого нужно использовать инструмент

Подбор параметра

(поле «Установить в ячейке» должно ссылаться на формулу с

ЧПС()

, в поле «Значение» установите 0, поле «Изменяя значение ячейки» должно содержать ссылку на ячейку со ставкой).

Расчет NPV при постоянных денежных потоках с помощью функции ПС()

Напомним, что

аннуитет

представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию

ПС()

(см.

файл примера, лист ПС и ЧПС

).

В этом случае все денежные потоки (диапазон

В5:В13

, 9 одинаковых платежей) дисконтируются на дату первой (и единственной) суммы инвестиции, расположенной в ячейке

В4

. Ставка дисконтирования расположена в ячейке

В15

со знаком минус. В этом случае формула

=B4+ЧПС(B15;B5:B13)

дает тот же результат, что и

= B4-ПС(B15;9;B13)

Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени

Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за

любые

промежутки времени, то используется функция

ЧИСТНЗ()

(английский вариант – XNPV()).

Функция

ЧИСТНЗ()

возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:

Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.

Принципиальным отличием от

ЧПС()

является то, что денежный поток привязан не к конкретным периодам, а к датам. Другое отличие: ставка у

ЧИСТНЗ()

всегда годовая, т.к. указана база 365 дней, а не за период, как у

ЧПС()

. Еще отличие от

ЧПС()

: все денежные потоки всегда дисконтируются на дату первого платежа.

В случае, когда платежи осуществляются регулярно можно сравнить вычисления функций

ЧИСТНЗ()

и

ЧПС()

. Эти функции возвращают несколько отличающиеся результаты. Для задачи из

файла примера, Лист ЧИСТНЗ

разница составила порядка 1% (период = 1 месяцу).

Это связано с тем, что у

ЧИСТНЗ()

длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у

ЧПС()

указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет

високосного

года).

Внутренняя ставка доходности ЧИСТВНДОХ()

По аналогии с

ЧПС()

, у которой имеется родственная ей функция

ВСД()

, у

ЧИСТНЗ()

есть функция

ЧИСТВНДОХ()

, которая вычисляет годовую ставку дисконтирования, при которой

ЧИСТНЗ()

возвращает 0.

Расчеты в функции

ЧИСТВНДОХ()

производятся по формуле:

Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).

Примечание5

. Функция

ЧИСТВНДОХ()

используется для

расчета эффективной ставки по потребительским кредитам

.